计量级磁悬浮转子真空计技术研究

习振华，郭美如，李博文，周明旭，2，李 宇，2，贾文杰，张虎忠，任正宜 ，成永军，李得天

（1.兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000；2.东北大学机械工程与自动化学院，沈阳 110819）

0 引言

磁悬浮转子真空计（Spinning Rotor Gauge，SRG）是一种精密的黏滞型真空计，以其优良的计量特性成为国际公认的高真空范围溯源/传递标准，常用于真空量值的国际比对以及各国真空量值溯源及传递体系的构建[1-4]。此外，磁悬浮转子真空计不会使气体分子解离和电离，且加热脱气后的磁悬浮转子真空计不会因为气体解吸而影响被测真空环境，从而在航空航天、核工业、半导体和高端装备制造等领域得到广泛的应用[5-6]。自20世纪80年代计量级磁悬浮转子真空计研制成功并商业化以来[7-8]，除德国LEYBOLD公司、VISCOVAC公司短暂研发以外，始终为美国MKS公司所垄断。近年来，许多国家及地区开展了相关研究以及同类及替代产品的研制[9-11]，但技术指标与MKS公司计量级磁悬浮转子真空计产品尚有差距。20世纪80年代，国内清华大学丛树人等[12-13]开展了磁悬浮高速转子真空计的初步研制。在长期研究磁悬浮转子真空计计量特性的基础上[5-6，14]，兰州空间技术物理研究所于2020年启动了计量级磁悬浮转子真空计的研制工作[15]，开展了永磁偏置转子稳定悬浮、转子轴向位移精确测量、残余阻尼抑制、转子转速衰减速率动力学模型构建及高精度检测等关键技术研究。

1 磁悬浮转子真空计工作原理

1.1 稀薄气体分子切向动量传递减速机理及压力反演数学模型

磁悬浮转子真空计的工作原理为气体分子与高速旋转的悬浮转子之间的摩擦力导致的转速衰减率与压力成正比。在高真空条件下，当分子的平均自由程大于转子和真空管壁之间的特征距离，并且当气体或物体表面以速度u运动时，施加在单位面积上的摩擦力为[1]：

式中：va为平均热运动速度；n为分子数密度；m分子为单个分子质量；δ为切向动量传递系数。

如果一个球形转子绕垂直z轴旋转，如图1所示，分子作用于表面使旋转的球形转子减速的力矩为：

式中：ω为旋转球形转子的角频率；R为转子半径；φ为分子在球形转子表面作用点半径与球形转子赤道面之间夹角。

分子数密度n（或压力p）的增大会导致分子阻尼力矩Mt按比例增加，分子阻尼力矩与旋转球形转子的惯性力矩相作用。由于惯性力矩MJ为角动量的一阶导数，且角动量ℓ=Jω，故：

式中：J为球形转子的转动惯量；t为时间。

因为球形转子是一密度均匀的对称体，故球形转子的转动惯量为：

式中：Jx、Jy、Jz分别为球形转子对应于x、y、z轴的转动惯量；ρ为球形转子密度；V为球形转子体积；m为球形转子质量；r为分子在球形转子表面作用点至旋转轴的垂直距离。

当温度随时间变化时，转子半径R可随时间变化，且转子半径随温度升高而增大，则转动惯量的相对变化为：

式中：α为球体材料的线膨胀系数；T为转子温度。

根据动量守恒定律，在理想状态下，动态平衡时，分子阻尼引起的力矩Mt与惯性力矩代数和为零。实际应用时，转子的磁悬浮状态会引入一个残余阻尼MR，该分量由涡流损耗引起，与压力无关。综上，可得到转子的相对减速速率：

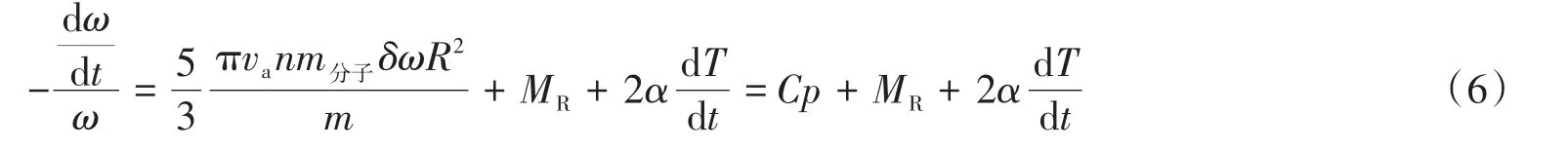
式中：C为常数，通过校准获得，与气体成分有关；p为压力。

1.2 转子转速相对衰减率测量及处理算法

转速相对衰减率不能瞬时确定，只能基于某一时间间隔内的平均值计算。由转子动力学理论可知，气体分子碰撞导致转子的旋转频率呈指数下降（旋转周期随时间呈指数上升）。因此，可通过测量转子旋转既定圈数所用的时间τ计算相对衰减率的平均值。

式中：τn、τn+1分别为相邻的时间间隔，且τn+1＞τn。

如图2所示，横向的时间轴代表整体旋转的过程，纵向的标记代表转子以某个特定角度转过一周时在信号感应（拾取）线圈上产生的信号脉冲，经过触发器与滤波成为图中的脉冲信号。随着转子在转动过程中的缓慢减速，右侧的时间标记之间的间隔总是略大于左侧的标记间隔（例如，10-4Pa的氮气压力导致转子旋转既定圈数时，相邻时间间隔的时间增量大约为10-7s），由此通过相邻周期来计算一定时间内的平均减速率。以转子转十圈为一个周期，τ1与τ2可以代入式（6）（7）计算出一个压力值，在紧随的下一周期进行新的计算。这种方法计算速度较慢，且易受到拾取信号分散性的影响。拾取信号分散性主要由测量电路相位噪声或时间抖动导致。故针对平均值的计算常采用多通道复周期平均法及复周期累积平均法进行。

图2 既定圈数时间间隔示意图Fig.2 Schematic diagram of time interval between the established periods

2 磁悬浮转子真空计关键技术及设计

磁悬浮转子真空计涉及机械、电子、自动化控制以及计量等众多学科，是一种典型的机电一体化产品，结构复杂、技术难度大、交叉耦合因素多。磁悬浮转子真空计从功能角度可分为单自由度永磁偏置转子悬浮系统、高速旋转驱动系统、水平抑制阻尼系统、强噪声背景下的微弱信号检测系统、主控系统等；从结构组成上可分为物理部分（传感器、法兰、转子）及电路部分。此外，作为计量级磁悬浮转子真空计，还需要重点解决非线性修正、残余阻尼抑制等突出问题，拓展测量范围，提高重复性、稳定性等计量特性指标。

2.1 磁悬浮转子真空计物理结构

磁悬浮转子真空计物理部分结构如图3所示。在非磁性套管（真空管）2的中心，一对稀土永磁体3产生的磁场为直径4.5 mm的球形转子1提供永磁偏置，并通过一对垂直稳定（悬浮）线圈4的合理布置，采用电磁力进行微小调整，使转子由永磁铁和垂直线圈的叠加磁场合力稳定在中心平衡位置。4个驱动线圈5呈4×90°正交分布，用以产生旋转磁场，使转子的旋转频率达到工作频率。磁悬浮转子真空计使用时，外部振动或冲击会引起转子的横向振荡，置于套管两侧的4个水平稳定线圈7（每侧两个）用于抑制转子的横向振荡。2个信号感应（拾取）线圈6可以感应到套管中球形转子的旋转磁矩，从而产生转子转速的周期信号。

图3 磁悬浮转子真空计物理结构示意图Fig.3 Schematic diagram of spinning rotor gauge

根据物理结构进行磁悬浮转子真空计物理部分的详细设计，模型如图4所示，主要包括法兰、套管、上支座、下支座、顶丝、转子、永磁体、线圈、线圈骨架以及磁屏蔽外壳等。其中，法兰用于磁悬浮真空计与真空室连接，采用CF40铜垫圈密封。法兰开有两个沉头螺钉孔，分别固定上支座和下支座。线圈及磁屏蔽外壳利用上下支座、顶丝进行固定。中心管采用无磁奥氏体不锈钢SUS316L加工。转子采用GCr15钢加工形成直径4.5 mm的G10等级球体，表面镜面抛光。磁屏蔽外壳采用坡莫合金加工，以减小漏磁。

图4 物理部分三维模型Fig.4 3D model of physical part

2.2 单自由度永磁偏置转子悬浮系统

由Earnshaw定理可知，仅用永磁体不可能实现静态稳定磁悬浮[16]。同时，鉴于无源磁悬浮结构稳定域小、易受外界激扰的特点，故采用有源磁悬浮结构，通过悬浮刚性转子刚体和阻尼的主动控制，克服前者可控度有限的缺点。采用永磁偏置加电磁混合励磁的结构实现球形转子的稳定悬浮。永磁体产生偏置磁场提供转子悬浮所需的大部分磁场，电磁线圈产生的磁场用以调节控制以保证悬浮稳定。在相同励磁容量的情况下，可以减小电磁线圈的匝数及其电感，提高系统响应速度，增强系统的稳定性，降低系统功耗进而减小温度对测量的影响。

单自由度永磁偏置转子悬浮系统组成如图5所示，主要包括传感器（悬浮线圈、永磁体部分）、高频激励信号发生电路（信号发生器、功率放大器）、前端调理电路（交流电桥、交直流信号耦合）、转子位移检测电路（差分放大、相敏检波）、悬浮控制电路（PID反馈控制、功率放大器）等。

图5 单自由度永磁偏置转子悬浮系统结构示意图Fig.5 Schematic diagram of SDOF levitation system based on permanent and electrical magnet

悬浮线圈为电涡流位移传感器，由高频交流激励驱动，转子偏离平衡位置时，两线圈公共端产生相对于激励信号的相位与幅值变化。包含位移信息的两路信号由前端调理电路交流电桥引出，经过相敏检波电路，检测出相位差，并经过调理电路产生直流信号，将此信号作为转子轴向位移的误差信号，传入PID反馈控制器，控制信号经过功率放大器后施加在线圈上，此时悬浮线圈亦作为悬浮控制的执行器，从而形成有效的闭环控制。

永磁体对悬浮转子的作用力需平衡转子重力。永磁体提供的磁力大小取决于距离及磁隙特性，确定永磁体直径后，相关数据代入式（8）：

式中：μup、μdown分别为上、下永磁体至转子的相对磁导率；Sm为永磁体面积；Br为永磁体剩余磁感应强度；Hc为永磁体矫顽力；Lm为永磁体厚度；y为上永磁体与处于中心平衡位置处转子的距离；m为转子质量；g为重力加速度。

方程的正实数根即为永磁体厚度的计算值，实际采用的永磁体厚度L'm=αLm，α为磁阻系数，针对不同的永磁体磁路，α取1.05～1.45。综上计算可得，永磁体厚度为3.5 mm，剩余磁感应强度为0.168 T。

悬浮线圈对悬浮转子的作用力为：

式中：μ0为真空磁导率；A为悬浮线圈横截面积；N为线圈匝数；i为线圈中电流；x为转子距离上悬浮线圈距离；k为比例系数，0＜k＜1。

当转子位于中心平衡点时，距上下悬浮线圈的距离相等，结合转子几何尺寸、涡流径向形成范围和透射深度，悬浮线圈采用空心螺线管型线圈结构，直径设计为9.5 mm，进而线圈匝数为：

式中：i0为转子位于中心平衡点时悬浮线圈中的电流值；x0为转子位于中心平衡点时距离上悬浮线圈的距离。

线圈的线径为：

式中：ρT为T℃时的导线电阻率；AT为线圈的磁势；LA为线圈每匝的平均长度；β为电压降系数；U为线圈的端电压。

螺线管线圈是一个电感器件，但不能按理想模型仅考虑感抗，还包括导线的阻抗以及容抗。线圈的电感与线圈的形状和层数相关，其电感如下：

式中：μ为磁导率；l为线圈长度；kc为长冈系数，与线圈的直径与长度比值相关。

在确定悬浮线圈电感值的基础上，根据线径、长度等信息，进一步得到线圈电阻：

式中：ρc为电阻率；Sc为导线横截面积。

综上可得，悬浮线圈匝数N=400匝，电感L=1 mH，电阻R=22 Ω。

2.2.1 高频激励信号发生电路

高频激励信号发生电路包括正弦信号发生器及功率放大器。正弦信号发生器用于产生幅值稳定的29 kHz高频正弦激励信号，原理图如图6所示。

图6 高频激励信号发生电路原理图Fig.6 Schematic diagram of high-frequency excitation signal generation circuit

由于MAX038产生的正弦信号峰-峰值仅为2 V，为提高悬浮线圈位移检测的灵敏度，需提高信号的幅值，并进行功率放大以提高线圈的驱动能力，放大后的高频激励信号峰-峰值可达10 V，如图7所示。本文选用功率放大器LM4700，该运放在输出功率为10 W时，其总谐波失真加噪声（THD+N）可低至0.005%。稳定低噪的功率输出有效提高了转子悬浮质量。

图7 高频激励信号测试曲线Fig.7 Test curve of high-frequency excitation signal

2.2.2 前端调理电路

前端调理电路主要用于与悬浮线圈构成双端平衡交流电桥，原理如图8所示。上下悬浮线圈与并联电容C1、C2构成了交流电桥桥臂的一侧，对应阻抗分别为Z1、Z2。当转子处于中心位置，电桥两臂压差为0，即电桥处于平衡状态，则Z1R2=Z2R1；当转子与悬浮线圈距离发生变化时，由于电涡流效应，悬浮线圈的等效阻抗发生变化，输出电压反映转子偏离平衡点的方向及位移大小。当转子移动时，电桥两臂温度漂移、干扰噪声等特性几乎完全一致。此外，检测位移所获得的直流反馈信号也由该电路耦合进悬浮线圈，实现转子悬浮位移的精确控制。

图8 前端调理电路原理图Fig.8 Schematic diagram of front-end modulation circuit

2.2.3 转子位移检测电路

转子位移检测电路由差分放大及相敏检波两部分构成，电路原理如图9所示。由前端调理电路获得的与位移相对应的电桥两臂电压信号经高精度放大器AD620差分放大后进入全波精密相敏解调器HJ002，与参考信号进行乘法运算，得到测量信号和参考信号的和频信号与差频信号。当输入信号和参考信号频率相同时，输出为直流信号。测量信号与参考信号分别为：

图9 转子位移检测电路原理图Fig.9 Schematic diagram of rotor displacement determination circuit

式中：Ui为测量桥臂测量信号电压；Ur为参考桥臂参考信号电压；a、b为测量信号与参考信号幅值；θ、β为测量信号与参考信号相位角；ω0为高频激励信号频率。

则相敏检波输出信号为：

式中：U0为相敏检波输出电压。

输出信号中包含交流分量和直流分量，滤去高频成分，输出的直流信号的幅值仅与输入信号的幅值成正比，而输入信号的幅值仅与转子位置引起的线圈阻抗变化有关。设计电路对应的位移检测灵敏度为1.33 mV/μm。

2.2.4 悬浮控制电路

悬浮控制电路主要由PID反馈控制其及功率放大器两部分组成，电路原理如图10所示。PID控制方法各参数物理意义明确，在工程应用中具有较好的准确性、稳定性、鲁棒性及动态特性，因此采用模拟PID控制方式实现转子位移误差信号的反馈控制。控制信号需要经过功率放大器放大才能驱动悬浮线圈，功率放大器采用与2.2.1节相同的功率放大器，不再赘述。

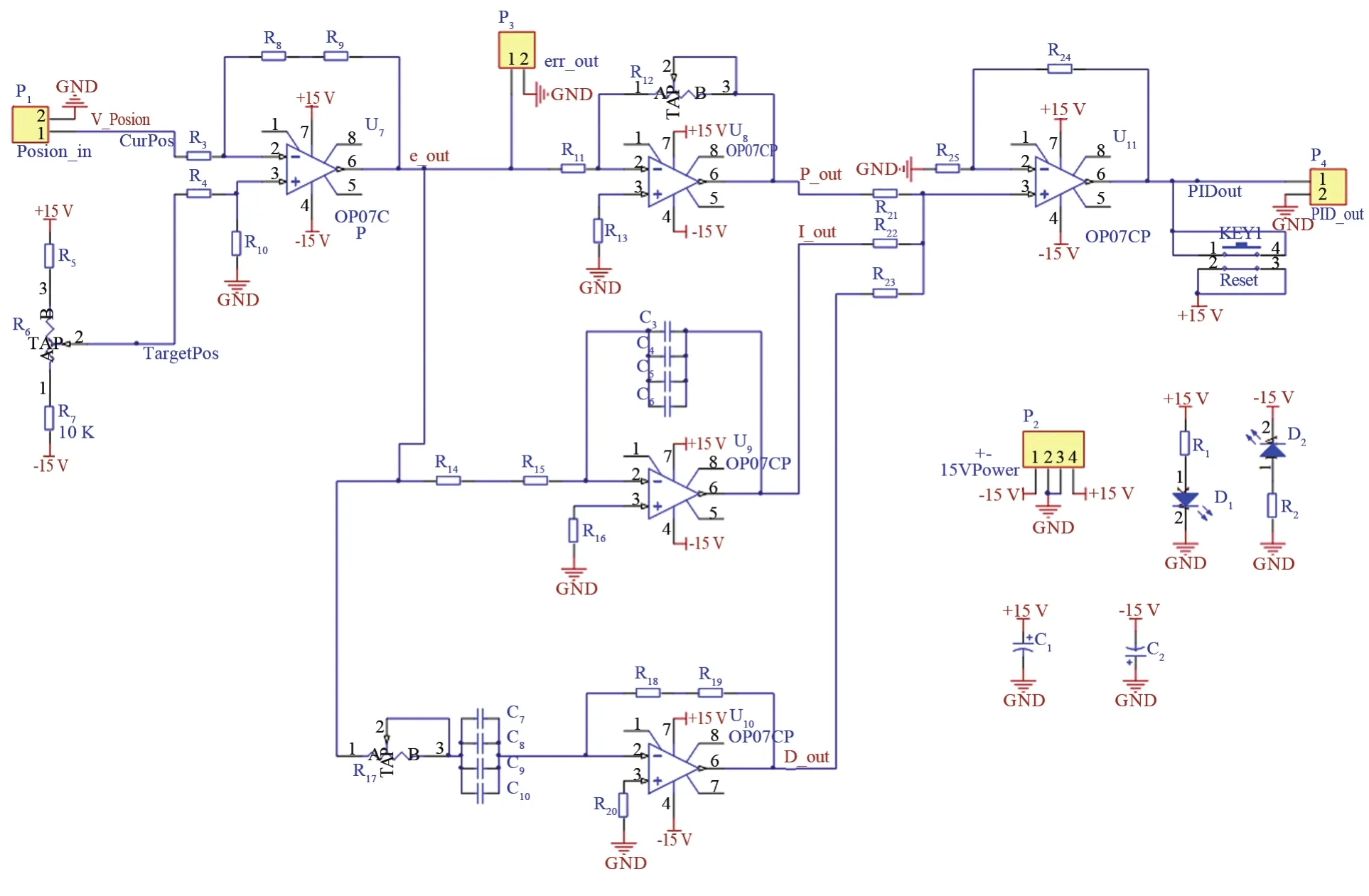
图10 悬浮控制电路原理图Fig.10 Schematic diagram of levitation control circuit

转子轴向悬浮的稳定性与残余阻尼的大小及波动量紧密相关。在传统磁悬浮动力学模型中，传感器与执行器是相互独立的，未涉及用于位移传感器的交流激励引入。但在磁悬浮转子真空计结构中，悬浮线圈既作为轴向位移检测的传感器，又作为使转子悬浮的执行器，因此用于位移检测的交流激励影响着直流分量悬浮控制的稳定性。通过引入交流影响因子aAC（用于表征在悬浮线圈加载直流信号以改变电磁力过程中，同时受到用于位移检测的高频交流激励信号的影响程度），并优化PID控制，可有效减小超调量及振荡次数，如图11所示，进一步提高悬浮稳定性。

图11 不同影响因子下的交流信号对磁悬浮响应过程的影响Fig.11 The influence of AC signals under different influencing factors on the response process of magnetic levitation

2.3 高速旋转驱动系统

转子的水平旋转通过在转子四周4个正交的旋转驱动线圈加载旋转磁场实现。如图12所示，与步进电机的驱动原理类似，向驱动线圈 L1、L2、L3、L4中通入两相中频交流电（其中两个线圈串联为一相，另两个线圈串联为另一相），主芯片为集成芯片L6228，电路原理如图13所示。由于转子被悬浮于空中且本身质量较小，水平旋转时质量可以忽略，相当于对无质量的转子进行驱动，即无负载，可以输出80 kHz频率的方波而保证不丢转。主控MCU控制电路转动脉冲信号和方向脉冲信号输出。

图12 驱动原理图Fig.12 Schematic diagram of drive

图13 步进驱动电路原理图Fig.13 Schematic diagram of step-type drive circuit

驱动电路对转子的加速曲线如图14所示。两次测量的平均加速速率分别为1.66 Hz/s、1.62 Hz/s，测量结果的差异主要来源于转子温度的差异，因为转子经旋转磁场驱动过程中会产生涡流进而导致其温度升高。

图14 转子加速曲线Fig.14 Rotational speed curve

2.4 强噪声背景下的微弱信号检测系统

2个信号感应（拾取）线圈可以感应到套管中球形转子的旋转磁矩，形成感生电动势，从而产生转子转速的周期信号，该信号仅为几十μV，且高频激励信号、旋转驱动信号在进行转速测量时为强背景噪声，因此，需采用高精度仪放INA103进行微弱电压信号的放大，该运放输入噪声为，增益带宽积为100 MHz。转速信号测量电路原理如图15所示。本设计中，放大倍数设置为1 000倍，放大后的信号经低通滤波器及比较电路滤波、整形后，得到与转速同频率的TTL方波脉冲信号，如图16所示。MCU采集该信号后进行转速衰减率测量。此外，转速信号的幅值与转速有关，实验表明，400～450 Hz转速范围信号幅值最大（如图17所示）。

图15 转速信号测量电路原理图Fig.15 Schematic diagram of rotational speed determination circuit

图16 转速测量曲线Fig.16 Measurement curve of rotational speed

图17 转速信号幅值测量曲线Fig.17 Curve of amplitude of rotational speed

分析可知，转子旋转时，磁极化轴与旋转轴具有夹角，如图18所示，随着转速的变化，夹角发生相应变化，故信号感应（拾取）线圈中对应的磁通量也发生变化，信号幅值亦发生改变。为保证测量信号质量，工作中心频率点选为440 Hz。

图18 转子旋转示意图Fig.18 Diagram of the rotor’s spin

3 磁悬浮转子真空计性能测试结果

采用国防最高真空计量标准——金属膨胀法真空标准装置对研制的磁悬浮转子真空计进行计量特性测试。

磁悬浮转子真空计压力示值误差按式（17）计算：

式中：Ei为压力示值误差；p为磁悬转子真空计压力示值；ps为真空标准装置生成的标准压力。

重复性按式（18）计算：

式中：Eri为磁悬浮转子真空计在对应压力点的重复性；Eimax为对应压力点示值误差的最大值；Eimin为对应压力点示值误差的最小值；dn为极差系数。

磁悬浮转子真空计性能测试结果如表1所列。

表1 计量级磁悬浮转子真空计原理样机计量特性实验结果Tab.1 The experiment results of SRG prototype’s metrological characteristics

4 结论

通过永磁偏置转子稳定悬浮、转子轴向位移精确测量、转子转速衰减速率动力学模型构建及高精度检测等关键技术的研究，研制了计量级磁悬浮转子真空计样机。实验结果表明，测量范围达到9.513 2×10-5～1.288 0 Pa。该样机的研制及后续优化改进将为建立我国现代先进的真空计量技术体系、真空量值溯源及传递体系，实现我国科技工业高真空范围真空量值国际等效奠定基础。