局部阴影下光伏电池MPPT算法的研究

李 明，来国红，常晏鸣，冯志强，马先超，耿家豪，王 港

（湖北民族大学 智能科学与工程学院，湖北恩施 445000）

引言

随着科技的进步，光伏技术在全世界范围内应用也越来越广泛[1]。但是在实际应用中，光伏电池容易受到环境的影响，从而造成局部阴影的问题，传统的电导增量法、扰动观察法、恒定电压法只能解决单峰值的问题，对于光伏电池的多峰值问题，传统的方法容易陷入局部最优，无法追踪到最大功率点，影响光伏电池的使用效率[2-6]。

针对局部阴影的多峰值问题，文献[7]提出多态蚁群-细菌觅食算法来实现部分遮蔽条件下光伏系统的最大功率输出。文献[8]改进天牛须搜索算法，通过对比扰动观察法与粒子群算法，验证其改进后的算法具有高效性。文献[9]提出把惯性权重自适应调整的量子粒子群与莱维飞行策略相结合的办法，减少了粒子在后期优化过程中陷入局部最优的问题。文献[10]提出一种粒子群算法与占空比扰动观察法相结合的方法，当光照强度变化时，可以相互切换，以提高光伏电池的效率。文献[11]提出了一种基于随机进化搜索和确定性爬山算法的光伏系统最大功率点跟踪方法。文献[12]采用人工蜂群集成扰动与观测（ABC-PO）MPPT 算法用于从光伏组件获得最大功率。文献[13]提出了一种基于确定性修正Jaya（DM Jaya）的算法来跟踪全局最大峰值。文献[14]提出了一种基于智能非对称模糊逻辑控制（AFLC）的最大功率点跟踪（MPPT）算法来跟踪多个峰值由单个全局最大功率点，与传统的扰动观测（P&O）算法和基于智能模糊逻辑控制（FLC）的GMPP 跟踪和阴影损失算法进行了比较，AFLC 算法具有一定的优越性。文献[15]提出了一种新的基于滑模控制器（SMC）的MPPT 算法框架，适用于具有部分阴影条件（PSC）和均匀条件的光伏板。

本研究针对粒子群算法在光伏最大功率追踪应用中存在收敛时间长，追踪效果差的问题，通过增加收缩因子与随机惯性权重相结合，再与扰动观察法相结合，解决在局部阴影下光伏MPPT 存在的问题，从而提高光伏电池的使用效率。最后，通过MATLAB/Simulink验证算法的可靠性。

1 光伏电池等效模型及特性分析

1.1 光伏电池数学模型

光伏电池是光伏发电系统最基础的单元，其发电原理是光电效应，当光照在光伏电池上时，P-N 结发生电荷移动，进而形成电势差，产生“光生电压”。在实际应用中，一般把光伏电池等效为电流源[16]。光伏电池等效模型如图1所示。根据基尔霍夫定律可得：

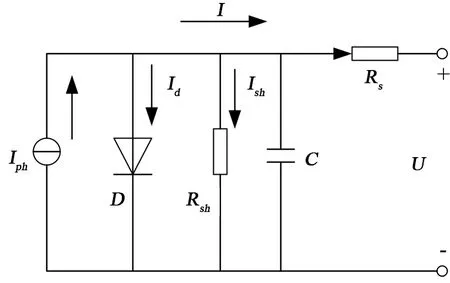
图1 光伏电池等效电路模型

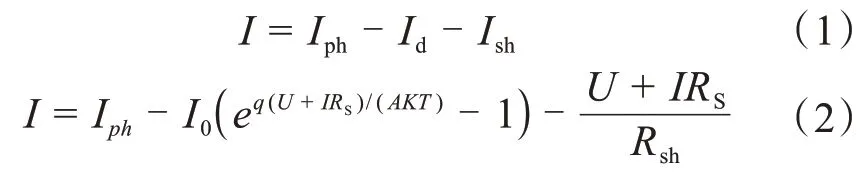
式中，I是光伏电池输出电流，U是光伏输出电压，Iph光生电流，I0是二极管反向饱和电流，q 是电子电荷常数1.6 × 10-19c，RS是串联电阻，Rsh是并联电阻，K是波尔玻尔兹曼常数1.38 × 10-23J/K，A 是P-N 结理想因子，一般取1，T是绝对温度。

实际电路计算中，这些参数都比较难确定，求解难度也比较大，因此将上述公式进行简化处理，推导出光伏组件工程的模型如下：

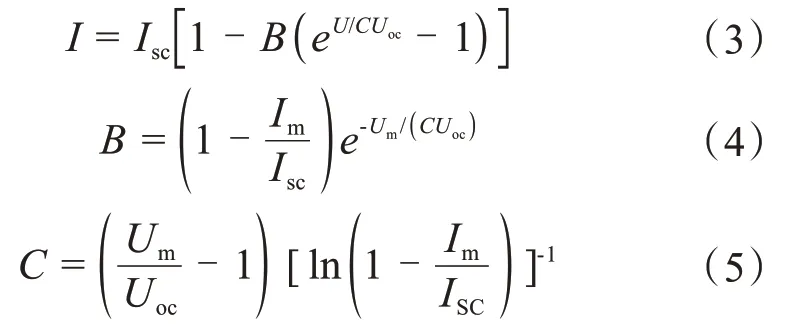
式中，Im是光伏电池的最大输出电流，ISC是光伏电池的短路电流，Um是光伏电池的最大输出电压，Uoc是光伏电池的开路电压。

由于环境、温度等影响，当光伏电池的工作条件发生变化时，通过对光伏电池数学模型等效参数的修改，得到新的工作情况下光伏组件[17]。

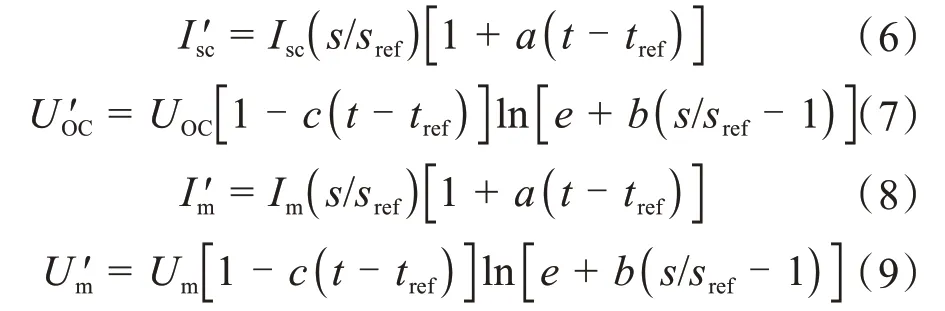
式中，tref=25 ℃，sref= 1 000 W/m2，a=0.002 5，b=0.5，c=0.002 88。

1.2 单个光伏电池特性曲线

单个光伏电池技术参数为Im=8.3 A，Um=30 V，UOC=36.8 V，Isc=8.83 A，其最大功率P=249 W，在温度为25 ℃，光照为600 W/m2，800 W/m2，1 000 W/m2条件下，其P-U，I-U特性曲线如图2所示。

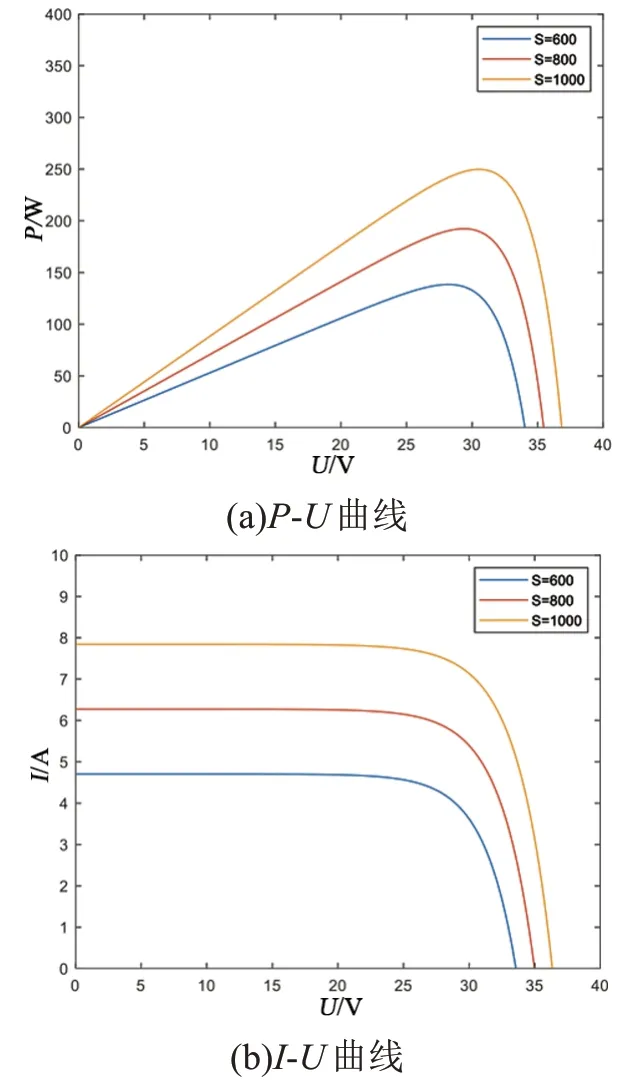
图2 不同光照下特性曲线

1.3 光伏阵列局部阴影条件下的模型

通过用四个光伏电池串联，在25 ℃的条件下，分别给予不同的光照来模拟局部光照，通过仿真可得最大功率点为550.915 W，最大功率点的电压为127.617 V，其P-U，U-I特性曲线如图3所示。

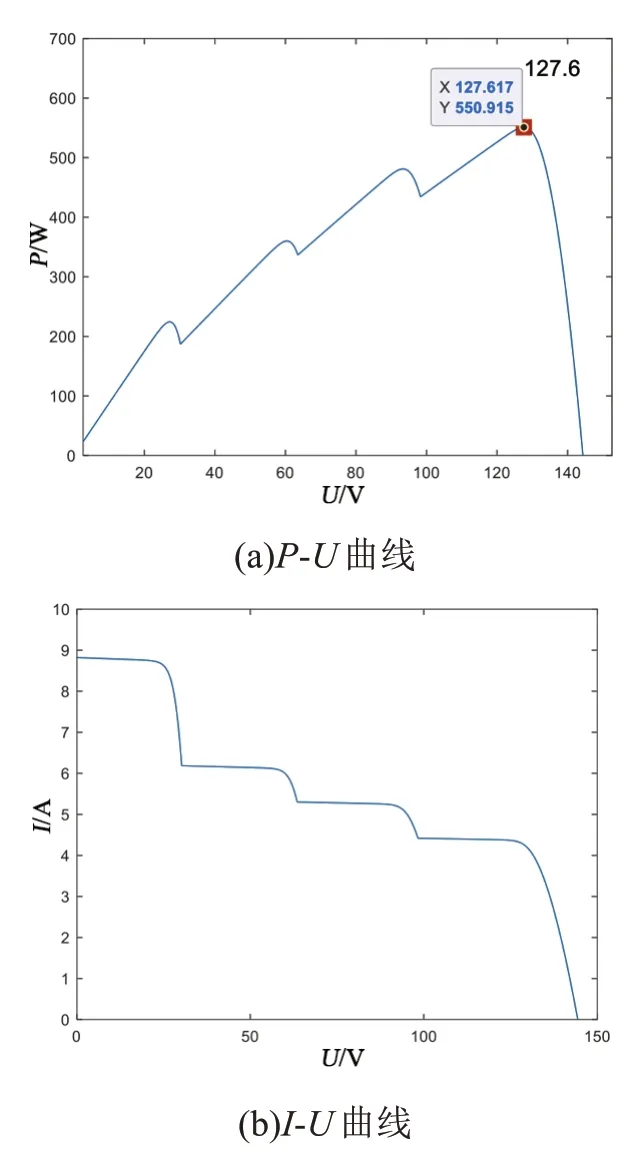
图3 光伏阵列特性曲线

2 算法介绍

2.1 扰动观察法

扰动观察法是光伏最大功率追踪常用的方法。该方法先通过扰动光伏阵列的输出电压，再对扰动后的功率进行监测，对比上一时刻与当前时刻的功率与电压的变化量，如果功率变化量与电压变化量同向，增加正向扰动；变化相反，则增加反向扰动。扰动观察法具有简单，容易实现，对于单峰值追踪效果特别好等优点，但是对于多峰值问题，很容易陷入局部最优。

2.2 粒子群算法

粒子群算法主要从鸟儿随机搜索食物的过程中得到的启发，并应用到实际情况中解决问题，基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。每个粒子主要有速度方向和位置方向两个主要参数，通过不断地更新来寻找最优解，其数学模型为：

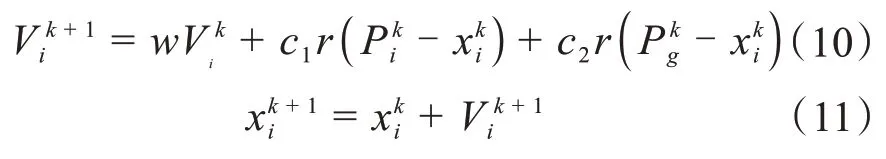
式中，V是粒子的速度方向，x是粒子的位置向量，r为（0,1）之间的随机数，i为粒子的序数，k为迭代次数，w为权重，c1和c2为学习因子，Pi是个体粒子最优解，Pj种群粒子最优解。其主要算法流程如图4所示。

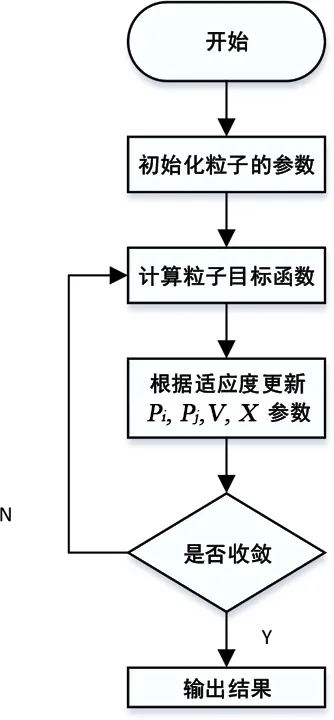
图4 粒子群算法流程

2.3 改进粒子群算法

根据粒子群的公式和分析可知，w为惯性权重，w越大，其全局搜索能力强，局部搜索能力较弱；w越小，全局搜索能力弱，局部搜索能力强。选择合适的惯性权重可以使算法更不容易陷入局部最优和减小震荡。c1和c2为学习因子，取值合适的c1，c2，具有平衡算法在局部开发和全局探索两个方面的作用。因此，权重w和学习因子c1和c2对粒子群算法具有重要意义。常规粒子群算法为固定参数，w一般取值0.4～0.9，而c1=c2常取2。本研究从以上两个参数进行改进。

（1）惯性权重改进，采用随机惯性权重，更新参数公式如下：

式中，Wmin为常数权重取值0.4，a取值0.5，r为0～1之间的随机数。

（2）增加收缩因子，其公式为：

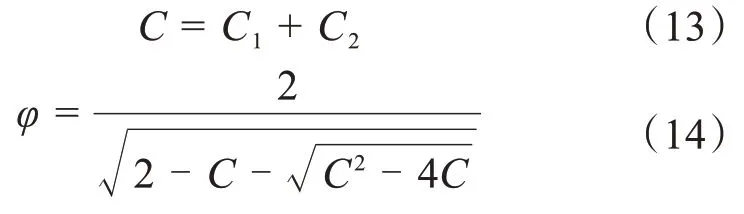
式中，C1=C2=2.05，将式（12）、（13）代入式（10）实现参数更新。

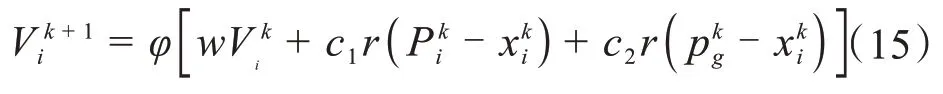
2.4 复合算法

对于局部阴影下最大功率追踪，先利用改进后的粒子群算法对最大功率进行追踪，当搜寻到最大功率点后，再切换至扰动观察法进行追踪，以减小其波动性，使其快速达到稳定。复合算法不仅能够加快粒子群算法收敛的速度，还能克服扰动观察法无法追踪到最大功率，从而陷入局部最优的问题，提高了追踪精度和准确率。

3 算法仿真

3.1 试验基础参数与环境

将4 块249 W 的光伏电池串联，单块光伏电池技术参数为Im=8.3 A，Um=30 V，UOC=36.8 V，Isc=8.83 A，在25 ℃条件下，分别光照为500 W/m2，600 W/m2，700 W/m2，1000 W/m2来模拟局部阴影光照，其最大功率为550.9 W。 Boost 电路参数为L=0.1 mH，C1=1 μF，C2=1 mF。光伏列阵仿真模型如图5所示。

图5 MPPT仿真模型图

采用MATLAB2022a，所用的计算机处理器为Ιntel(R)Core(TM)i5-6300HQ CPU@2.30 GHz，内存为16.0 GB 进行仿真。分别采用扰动观察法、粒子群算法、改进后的粒子群算法和复合算法分别进行仿真，仿真时间均设置为2.5 s。

3.2 扰动观察法仿真

扰动观察法仿真图如图6 所示，由图6 可知在0.1 s时，输出的功率达到稳定（228 W），这远远小于四块光伏电池局部阴影下最大功率550.9 W，说明扰动观察法在此刻已经陷入局部最优，无法追踪到该四块光伏电池的最大功率。

图6 扰动观察法下最大功率追踪

3.3 粒子群算法仿真

粒子群算法采用6 个粒子，惯性权重w=0.4，学习因子c1=c2=2.05 的条件下进行仿真，仿真结果如图7所示，由图可知在1.5 s处捕获到最大功率点，为550 W，但是还处于波动中。

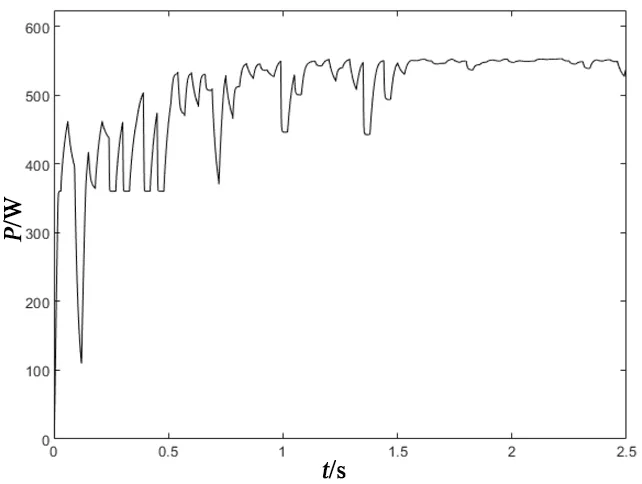
图7 粒子群算法下最大功率追踪

3.4 改进后粒子群算法仿真

改进后的粒子群算法，采用随机权并且增加收缩因子，同样采用6 个粒子，仿真图如图8 所示，可以明显看到该算法能够更好地捕获最大追踪功率点，在1 s 时找到最大功率点。相比改进前，提前0.5 s就找到最大功率点，并且波形稳定。

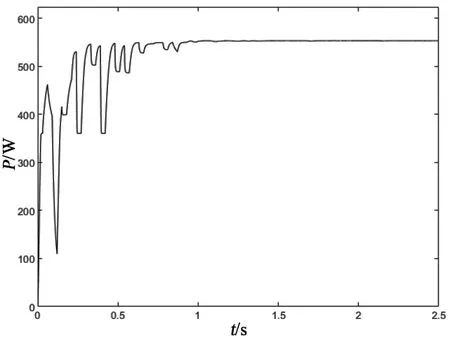
图8 改进粒子群算法下最大功率追踪

3.5 复合算法仿真

采用复合算法，仿真图如图9 所示。从图9 可见，在0.4 s 就找到了最大功率点，比改进后的粒子群算法提前0.6 s，输出的波形更加稳定。

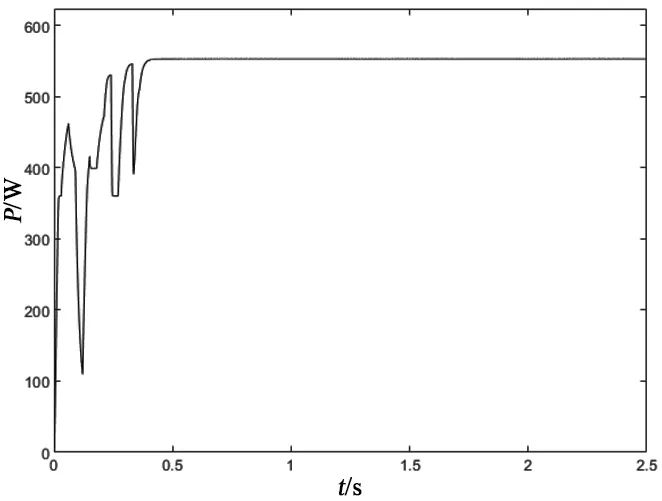
图9 复合算法下最大功率追踪

3.6 试验总结

通过以上对比试验分析可知，复合算法相比普通粒子群算法提前1.1 s 找到最大功率点，并且输出的波形稳定，比改进后的粒子群算法提前0.6 s 找到最大功率点，也能克服扰动观察法陷入局部最优的缺点，充分验证了复合算法搜寻的精确性和速度性。

4 结论

针对局部阴影光照下，光伏电池输出功率呈多峰值的问题，提出了一种改进粒子群算法与传统扰动观察法相结合的算法，然后在MATLAB Simulink中进行仿真。通过仿真试验可以看出，粒子群算法可以有效地解决传统扰动观察法下局部阴影下无法找到最大功率点的问题，并通过改进粒子群算法，使得粒子群算法可以收敛更快，更稳定地找到最大功率点，再结合扰动观察法，进一步提高了搜寻速度和精度。