基坑开挖对下卧既有地铁隧道变形规律研究
李斌李小彤辛公锋秦思远张娜
(1.青岛市市政工程设计研究院有限责任公司,山东 青岛266000;2.山东大学 齐鲁交通学院,山东 济南250061;3.山东高速工程检测有限公司,山东 济南250000)
0 引言
交通强国战略的提出,促进了地铁行业的发展。地铁隧道施工过程中,在下卧既有地铁隧道条件下,基坑工程的开挖极易改变隧道原有应力平衡状态,使周围土体出现不同程度的应力释放,导致隧道变形;当变形值超过设计允许值时,隧道衬砌会产生开裂渗漏,从而影响隧道的安全稳定[1-2]。 目前,在北京、上海、深圳等地区,有关基坑工程邻近或相交既有地铁隧道的工程研究较为成熟,而在青岛地区上软下硬的地质条件下类似研究较少。 因此,研究适合青岛地区地质条件的基坑开挖时下卧既有地铁隧道的变形规律,对于该地区基坑安全施工、控制隧道变形、提高隧道运营的安全稳定等具有重要的现实意义。
目前的研究主要采用Mindlin 理论计算作用于隧道的附加应力,并基于弹性地基梁理论计算隧道变形值。 青二春[3]基于Mindlin 理论,提出了基坑开挖时坑底不同位置处附加应力计算公式,并结合折减系数法与分层总和法,计算得到下卧既有地铁隧道的隆起变形量;肖同刚[4]以上海某存在邻近隧道的基坑开挖工程为例,通过对基坑开挖过程的动态监测,全面分析基坑开挖对邻近运营地铁隧道产生的影响;张建斌[5]基于Boussinesq 解与Mindlin 解,提出土岩起伏地层中基坑开挖引起下卧地铁隧道变形的半解析预测方法;刘建文等[6]采用Mindlin 解对基坑开挖过程中下卧盾构隧道的变形计算开展研究。
综合考虑基坑-土体-隧道的共同作用,揭示基坑开挖对隧道变形的影响,采用FLAC3D、ABAQUS、MIDAS/GTS 等数值分析软件开展了大量研究[7-10]。文章依托青岛梅岭东路地下通道工程,提出了基坑开挖时隧道附加应力与变形量计算的实用公式;利用有限差分软件FLAC3D,研究基坑开挖过程对下卧既有地铁隧道的变形规律。 研究成果对类似地区基坑工程的安全施工和控制下卧地铁隧道变形有一定的参考价值。
1 基坑开挖下卧既有地铁隧道变形理论计算
1.1 矩形基坑开挖卸载所引起的附加应力的计算
采用附加应力解析法,通过Mindlin 解求出作用于隧道结构上的附加应力[11]。 Mindlin 理论计算模型将基坑上方的土压力简化为作用于基坑的均布荷载q。 假设基坑开挖长度为L、宽度为B、深度为h,隧道位于基坑下z0深度处。 隧道纵轴线与荷载平面方向平行、与荷载轴线成α角时的基坑计算模型简图如图1 所示。

图1 附加应力计算模型示意图
根据Mindlin 理论,假设(x,y,d)处作用一集中力Q,则半无限体内某一深度z0处任一点(x0,y0,z0)在集中力Q的作用下,竖向附加应力σz由式(1)表示为

式中υ为土体泊松比;R1为集中力作用点与所求点距离,m;R2为集中力作用点与所求点地面对称点距离,m。 其中,
根据图1 的计算模型,将均布荷载q带入式(1),可得隧道任意一点(x0,y0,z0)处的附加应力。取微分单元dξdη,其所受荷载Q=qdξdη,则由荷载引起的隧道轴线任意一点(x0,y0,z0)处的竖向附加应力σz由式(2)表示为

式中dξ为荷载沿x方向的作用面长度;dη为荷载沿y方向的作用面长度;U为荷载作用面积分区间。
依据工程实际,建立矩形基坑开挖模型如图2所示。
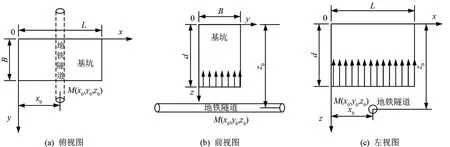
图2 矩形基坑开挖计算模型
矩形基坑坑底产生的竖向卸荷为σv=-γd,在隧道轴线任意一点M(x0,y0,z0)处,所产生的竖向附加应力σz由式(3)表示为

式中γ为 土体重度,kN/m3。
因此,若已知基坑尺寸、土体参数、基坑中心与隧道轴线的距离,则可求得基坑开挖对下卧既有地铁隧道轴线上任一点M(x0,y0,z0)产生的附加应力理论值[12]。
1.2 下卧地铁隧道的纵向位移计算
基坑开挖过程中,隧道可近似为地基梁,则隧道与土体的变形可简化成地基梁与土体在相互作用下产生的共同变形。 因此,根据Winkler 弹性地基梁理论,隧道结构与土体之间相互作用的力学方程由式(4)表示为

式中EI为隧道等效抗弯刚度,kN·m2;dx为梁中一微段;s(x)为梁与土体的沉降,mm;K为弹性地基的抗压刚度系数;p为隧道变形引起的地基反力,kPa;q(x) 为基坑开挖时作用于隧道结构的荷载,kPa,q(x)= σz × D,其中D为隧道外径,m。
Winkler 弹性地基无限长梁地基模型认为由隧道变形引起的地基反力p=Ks(x),此时式(4)可换算成式(5)表示为

求解式(5)得到在集中力作用下,地基梁原点处的方程解由式(6)表示为
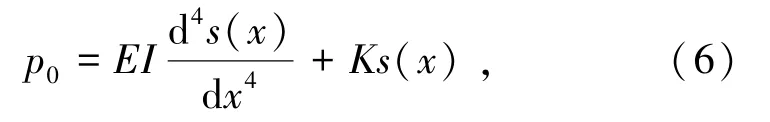
式中p0为集中力作用下地基梁原点处的地基反力,kPa。
根据荷载、地基梁位移等边界条件得到式(6)的解由式(7)表示为


式中q(ε)为作用在隧道结构上任一点ε处的集中荷载,kPa。
对式(8)进行积分计算,得到由附加荷载引起的位移量方程解由式(9)表示为
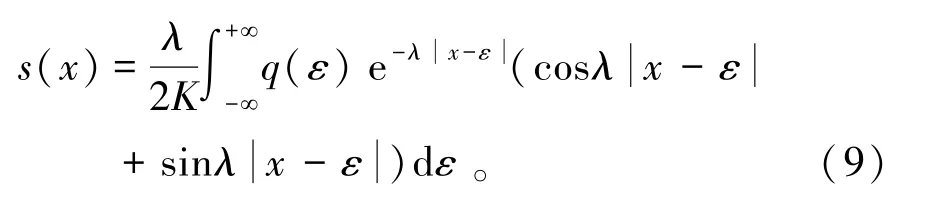
2 数值模型建立
2.1 工程概况
梅岭路地下通道位于青岛市崂山区梅岭路,工程西起海尔路、东至云岭路以西,地下联络通道工程基坑沿梅岭东路东西向布置,其长度约为60 m、宽度为40 m、深度约为8.0 ~8.5 m。 基坑围护结构的西部为钻孔灌注桩+旋喷桩+锚索,其他方向为放坡+锚(杆)支护。 根据现场施工条件,为便于计算,文章主要以基坑主体西侧为研究对象开展数值模拟,支护形式为钻孔灌注桩与锚索支护,具体支护形式如图3 所示。
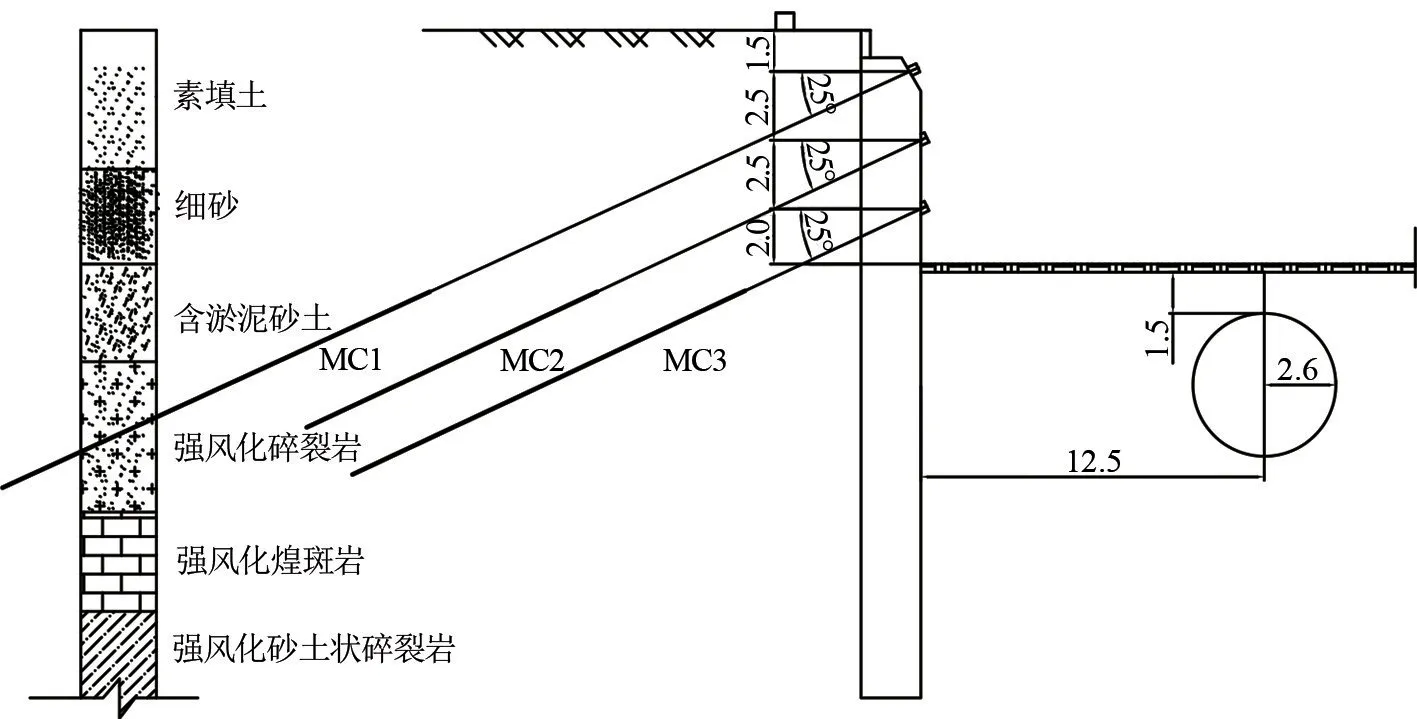
图3 基坑西侧支护形式/m
2.2 模型几何尺寸及材料参数
随着建筑技术的不断优化,数值模拟分析已成为解决类似基坑工程问题最为普遍的方法[13-14]。采用FLAC3D 有限差分软件建立模型。 假定土体为连续、均匀、各向同性弹塑性体,不考虑尺寸效应;同时不考虑基坑开挖与降水的影响;开挖后立即进行支护,待变形稳定后再开展后续开挖。 模型基本参数假设如下:
(1) 钻孔灌注桩 假设为弹性材料,用实体单元进行模拟,采用弹性模量E=3.0×104MPa、泊松比υ=0.3、密度ρ=25 kg/m3。
(2) 衬砌结构 壁厚300 mm、密度ρ=24 kg/m3、弹性模量E=2.0×104MPa、泊松比υ=0.2。
(3) 锚索 假定为弹性材料,采用锚索Cable单元进行模拟,基坑分层开挖到锚索设计位置处,钻孔并施作锚索。
(4) 土体 利用六面体实体单元进行模拟,采用摩尔-库伦本构模型[15]计算。 由地勘资料可知,施工现场土层分类较多、模拟存在困难,因此选择一定深度范围内性质相近的土层进行合并计算,所得参数见表1。
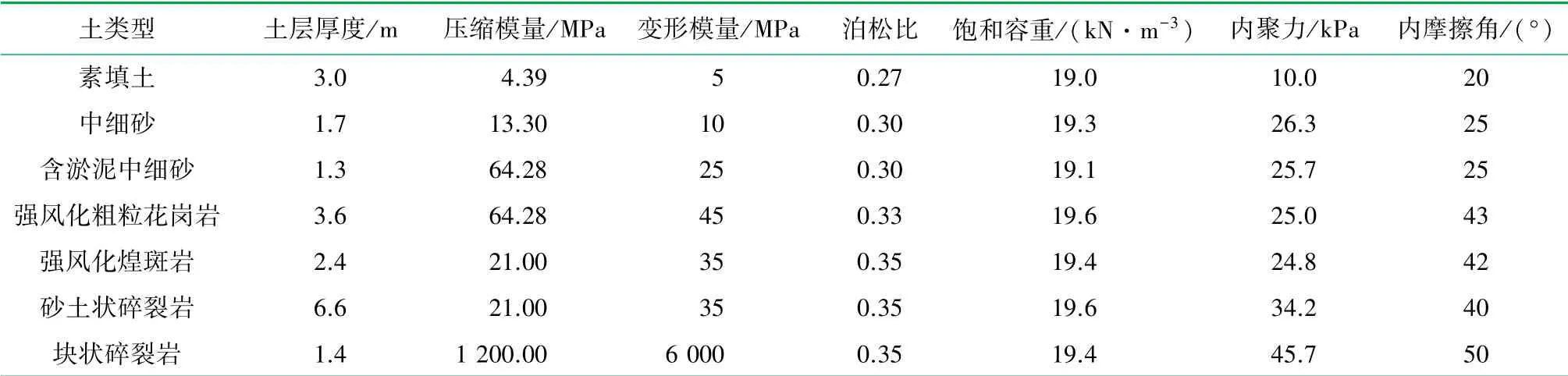
表1 土层参数表
计算模型如图4 所示,根据已有经验及基坑开挖的影响范围,模型尺寸为70 m×1 m×40 m(长×宽×高),隧道的拱顶埋深取10 m、隧道直径为5.2 m、衬砌厚0.3 m,钻孔灌注桩距隧道中心的距离为12.5 m。

图4 基坑计算模型简图/m
2.3 基坑开挖过程模拟
为更真实地模拟基坑开挖卸荷对下方既有隧道变形的影响,需在隧道开挖完成后清零土体位移。基坑开挖及支护过程有4 个施工,分别为(1) 土体开挖到地表以下1.5 m 处,设置第1 道锚索;(2) 土体开挖到地表以下2.5 m 处,设置第2 道锚索;(3) 土体开挖到地表以下6.5 m 处,设置第3 道锚索;(4) 土体开挖到地表以下8.5 m 处,设置第4 道锚索。
施工前,土体处于初始应力平衡状态。 如图5所示,基坑开挖后,由于开挖卸荷作用,土体的原有应力状态受到破坏,导致土体应力重分布[12],引起围护结构趋于向坑内水平移动,基坑底部由于坑内土体不断卸荷,产生明显隆起。

图5 基坑开挖完成后整体位移矢量图
3 数值模拟结果与分析
3.1 基坑开挖后桩后土体地表沉降值对比
为验证数值计算的正确性,先进行基坑开挖后桩后土体地表沉降规律的分析,其数值计算结果和现场实测结果如图6 所示。 基坑开挖后桩后土体地表沉降的数值计算值与现场实测值的变化趋势基本吻合。 距钻孔灌注桩较近处,桩后土体出现微小隆起;随测点位置与钻孔灌注桩距离的增大,土体呈沉降趋势;距基坑外围护桩20 m 处,沉降值最大为2.03 mm。 二者的对比结果初步验证了数值计算方法的正确性。
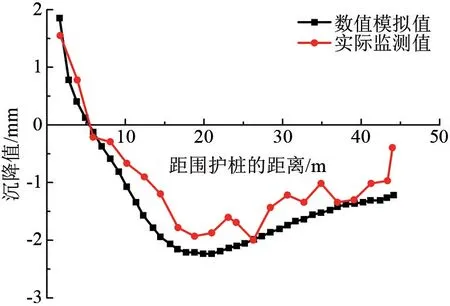
图6 基坑开挖后地表沉降变化对比曲线图
3.2 基坑开挖对隧道衬砌结构位移的影响
隧道周围喷射混凝土形成隧道-支护-围岩的复合承载形式,可提高隧道安全性与耐久性。 为准确描述基坑开挖过程中隧道衬砌结构的变形情况,分别在衬砌结构拱顶、两侧拱腰和拱底位置处设置监测点,如图7 所示。

图7 监测点布设示意图
3.2.1 竖向位移
(1) 理论公式计算
计算矩形基坑开挖引起的附加应力与隧道的竖向位移,将其与数值结果对比分析以进一步验证数值模拟的准确性。
根据工程实际,隧道外径D=5.8 m、纵向抗弯刚度EI=6.73×107kN·m2、综合地基基床系数k=1×104kN/m3。 由实际工程的地勘资料可知:第一层开挖土体υ=0.27、γ=19 kN/m3;第二层开挖土体υ=0.30、γ=19.3 kN/m3;第三层土体υ=0.30、γ=19.1 kN/m3;第四层土体υ=0.33、γ=19.6 kN/m3。式(7)中的
因计算公式复杂、计算量大,借助数学软件Matlab 进行编码计算。 利用式(3)计算基坑开挖引起的附加应力值,利用式(7)计算各施工步下的隧道位移变形量。 计算得到各施工步产生的附加应力值分别为-26.21、-70.75、-115.03、-149.49 kPa;基坑开挖完成后隧道衬砌结构的最大位移变形量为5.63 mm。
(2) 数值模拟计算
基坑土体竖向位移的数值计算结果如图8 所示。 随着基坑开挖,深层土体表现为向基坑内移动的变形,基坑内土体则在多向土压力作用下发生隆起;坑外土体发生地层应力损失,导致坑外地表沉降,基坑底部的竖向变形较大;基坑开挖完成后坑底的最大变形量为12.8 mm。

图8 土体竖向位移等值线云图/mm
隧道衬砌各监测点随基坑开挖施工步骤的竖向位移曲线如图9 所示。 在基坑开挖过程中,隧道衬砌结构顶部的竖向变形最大,具体表现为:开挖过程中基坑内土体逐步减少,地应力重新平衡,隧道整体出现竖向变形;前期变形较缓,随开挖进行逐渐增大,直至开挖完成竖向变形趋于稳定,最大竖向位移为9.35 mm。
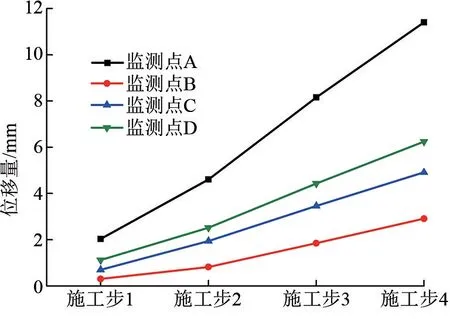
图9 隧道衬砌各监测点竖向位移变化曲线图
为进一步验证数值模拟方法的合理性,对比分析隧道衬砌结构竖向变形的理论值与数值模拟结果可知:二者的变形结果均随基坑开挖深度地增加而增大;受基坑施工过程中多种因素的影响,理论值略小于数值模拟结果。
3.2.2 水平位移(收敛)
图10 为基坑开挖过程中隧道衬砌结构横截面上4 个监测点的水平位移值。 计算表明,隧道的水平位移量与基坑开挖深度整体成正相关;但随开挖深度地增加,各点的水平位移变化规律各不相同,拱顶、左拱腰处监测点的增长幅度明显大于拱底、右拱腰处监测点;开挖完成后衬砌结构的水平位移总体呈“左大右小”,其最大水平位移为2.15 mm。 分析其原因:基坑开挖过程中,隧道上部荷载变小,衬砌所受围岩压力产生变化,引起衬砌结构变形,由于拱顶监测点距基坑底部距离最小,因此该点变形更大;开挖过程中由于开挖卸荷作用,基坑两侧土体的土压力不断增大,导致围护桩趋于向基坑内移动,相较于拱底、右拱腰处监测点,左拱腰处监测点距钻孔灌注桩较近,因此其收敛变形受影响程度更大。
综合上述研究发现,在基坑开挖过程中,衬砌顶部发生了自身变形及整体上抬变形的叠加,衬砌底部位移量小于顶部位移量;基坑开挖完成后,隧道衬砌结构总体呈向基坑方向隆起的变形趋势;受基坑开挖的影响,隧道衬砌结构的横断面表现出水平方向压缩、竖直方向拉伸的“椭圆形”变形特点。
4 结论
依托青岛梅岭东路基坑工程,推导并提出了适用于下卧既有地铁隧道的基坑工程开挖时隧道附加应力与变形量的计算公式,并采用有限差分软件FLAC3D 进行数值计算,对比分析了地表沉降与隧道变形的理论、实测、数值结果,得出的主要结论如下:
(1) 在基坑开挖过程中,随测点位置与钻孔灌注桩距离的增大,桩后土体隆起量逐渐减小产生沉降;距钻孔灌注桩20 m 内,围护桩后地表沉降与测点距围护桩距离成正相关,其沉降量最大为2.03 mm;基坑外距围护桩20 m 位置处,土体沉降量最大,随施工而逐渐趋于稳定。
(2) 隧道衬砌结构竖向、水平位移均随基坑开挖施工步的进行逐渐增大,隧道衬砌结构竖向与水平最大位移量与基坑开挖深度呈正相关,至基坑开挖完成其最大值分别为9.35 和2.15 mm。 隧道衬砌结构整体呈现水平方向压缩、竖直方向拉伸的变形特点。

