前庭6-PSS康复机器人洗出算法运动轨迹研究

孙智慧，桑 华，晏祖根，窦家明

(哈尔滨商业大学 轻工学院，哈尔滨 150028)

随着社会发展和老年人口的增长，平衡障碍的发病率随之增加，发病率高达0.5%～1%，平衡障碍是导致老人跌倒、失能和伤害死亡的首位原因，所致经济损失超过1 000亿元/a[1].究其原因，平衡障碍成因复杂，临床量化评估客观标准缺失，干预和康复针对性差，严重依赖医生专业水平[2].跌倒是人体对自身失稳状态的平衡调节能力不足导致的结果，跌倒原因复杂，过程多变，研究跌倒过程，是个性化分析平衡能力的关键[3]；采用生物、运动信息采集系统，采集平衡障碍患者常见跌倒行为的过程信息，提取跌倒运动的空间、时间参数，分析跌倒轨迹的特征，建立跌倒运动特征模型，为模拟失稳环境提供依据[3].前庭是人体感受平衡状态变化的重要器官，通过感受人体头部的角度、加速度的变化量，向人体中枢系统输入人体平衡状态特征，触发前庭觉.采用并联机器人构型，驱动机器人末端致使人体运动，给予头部有一个特定的加速度变化，使人体包括头部产生位移变化被前庭器官捕捉，从而产生前庭觉.而新型的康复机器人结合了医学理论和机器人工作原理，通过对人行走状态的动感模拟，加强了对下肢肌肉锻炼的同时也使神经系统的控制力得到逐步恢复，从而最终使患者康复达到正常行走的目的[3].

1 前庭康复并联机器人结构设计

6-PSS运动平台是康复机器人的主要承载机构，机器人由动平台、基座(静平台)、六条运动支链等组成，单条运动链是由直线电机驱动在竖直方向运动，电机球铰接支杆带动支杆末端运动，支杆另一端球交接于动平台.其结构如图1所示.

图1 前庭康复6-PSS并联机器人系统Figure 1 Vestibular rehabilitation 6-PSS parallel robot system

1.1 平台机构自由度计算

6-PSS运动平台属于空间机构，呈闭环状，所以自由度计算应使用KG计算公式[4]

(1)

其中：M为式中自由度的数目，n为式中构件的个数，fi为第i个的运动副相对自由度数，g为式中n个物体的运动副数量.

1.2 空间坐标系建立与转换

6-PSS平台机器人的动作输出端是上动平台，应对动平台建立一个动坐标系描述其运动，下静平台建立静坐标系对动平台的运动进行计算处理.因此需要对动静坐标系之间的转换矩阵求解[3].

六自由度平台结构示意图如图2所示，构建按机器人动坐标系P-XPYPZP于静坐标系O-XYZ.静坐标系的原点与大地坐标系原点重合，支撑杆AB长为L.在上平台位于中间位置时，静坐标系和动坐标系的各个方向轴平行，X轴和Y轴互相垂直构成静平台所在底面，Z轴垂直于此平面且向上.动坐标系下的X轴与Y轴互相垂直后成动平台所在平面，动坐标系下的Z轴垂直于此平面向上，且在中立位置时，两坐标系下的Z轴重合.上平台的各个铰链看作一套坐标点，分别为Ai(i=1,2,3,4,5,6),与基座滑块相连的球铰链看作另一套坐标点，分别为Bi(i=1,2,3,4,5,6)，下平台滑块坐标设为Ci(i=1,2,3,4,5,6).

图2 6-PSS平台机构简图Figure 2 6- PSS platform mechanism diagram

在康复机器人中输入的是动坐标系P-XPYPZP里的信号，洗出算法运算时需要静坐标系O-XYZ下的信号，所以转换矩阵必须还要对上式矩阵进行逆的运算，从而求出式(1)的逆矩阵，即从动坐标系转换成静坐标系的转换矩阵为：

(2)

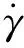
角速度转换矩阵TIS如下所示.

(3)

2 人体感觉系统

为了使动感模拟器平台上实现真实的体验感受，首先需要了解人体感知系统，人体感受运动主要分为运动深感觉、前庭觉、视觉神经信号.而维持身体平衡是一项非常复杂的信号处理过程，需要配合以及中枢神经完成的，视觉感知可以通过虚拟现实技术实现，运动深感觉与前庭觉则需要重点研究关于根据前庭系统特性的平台运动洗出算法[6]做出特定动作来完成.

2.1 人体前庭系统

人体的运动变化感知系统的原理在目前已经有了很多研究结果，其主要结构单元是位于大脑耳部中的前庭器官，因人体运动感觉平衡系统极其复杂，但感知运动加速度和角速度的部分是由人体耳石器官与半规管器官构成，根据医学临床实验分析出模拟人体前庭的数学模型[4].人体移动产生的绝对加速度结合有可能由转动的绝对角速度结合而成的综合加速度，再通过建立的耳石模型后是人脑部感知的加速度；而人体的绝对角速度在经过数学模型后分解曾三个方向人体感知的角速度[5].

2.1.1 耳石模型

前庭器官耳石结构是一圈带有纤细绒毛的细胞，其排列固定大小不一[4].能够感知出来人的头部的所在位置和其所收到的重力的相对变化，这些毛细胞因运动产生的绒毛波动导致差异性刺激从而产生信号传递大脑皮层.经大量实验的认证，耳石器官的功能是感知人体线性加速度，但并不是直接感知，是感知重力分量——力比.即绝对加速度减去重力加速度.如式(4)所示：

fAA=a-g

(4)

当人体头部产生加速度时，耳石器官可以感知其存在，但并不能判断其来源，即耳石器官没有办法分别加速度来源与运动还是重力分量.所以利用这一点可以在相对静止或有限的运动空间制造出持续的加速度信号让耳石器官感知.人体耳石模型最早是由Young和Oman[8]提出，如图3，表1所示.

图3 耳石模型Figure 3 Otolith model

表1 耳石模型的参数

经过计算得到耳石模型的传递函数如下式：

(5)

2.1.2 半规管模型

半规管结构是人脑部前庭器官另一关键部位，是感觉角速度的主要器官[4]，实际角速度经过人体半规管后，可以感应到分别围绕XYZ轴的三个方向的角速度，但角速度在传递时存在一个阈值，在该值范围内脑部前庭察觉不到旋转动作的发生.见图4.

图4 半规管模型Figure 4 Semicircular canal model

半规管模型的传递函数为：

(6)

2.2 经典洗出算法

当人体头部产生加速度时，耳石器官可以感知其存在，但并不能判断其来源，即耳石器官没有办法分别加速度来源与运动还是重力分量.所以利用这一点可以在相对静止或有限的运动空间制造出持续的加速度信号让耳石器官感知.而角速度是由人体重的半规管器官感知，由半规管模型知，感知的角速度已经是绝对角速度，所以在后续中限副处理便可直接作为输入信号[8].

洗出算法的结构图如图5所示，其输入的加速度aAA和角速度ωAA是上平台质心所需要模拟运动的数据.而输出信号是洗出后符合动感模拟的数据，即动平台对静平台的位移Sl和姿态角βl.

图5 经典洗出算法的原理图Figure 5 Schematic diagram of the classical washing out algorithm

2.3 洗出算法仿真分析

在机器人平台运动算法仿真过程中，使用MatlabSimulink使用对应模块对洗出算法进行仿真.由图6建立的经典洗出算法模型中可以得到俯仰和纵向的算法框图[11].在此过程中加速度通道忽略角速度的影响，在选择和设计各个滤波器的自然截止频率和阻尼系数，需要通过相关经验和对应的平台测试数据.

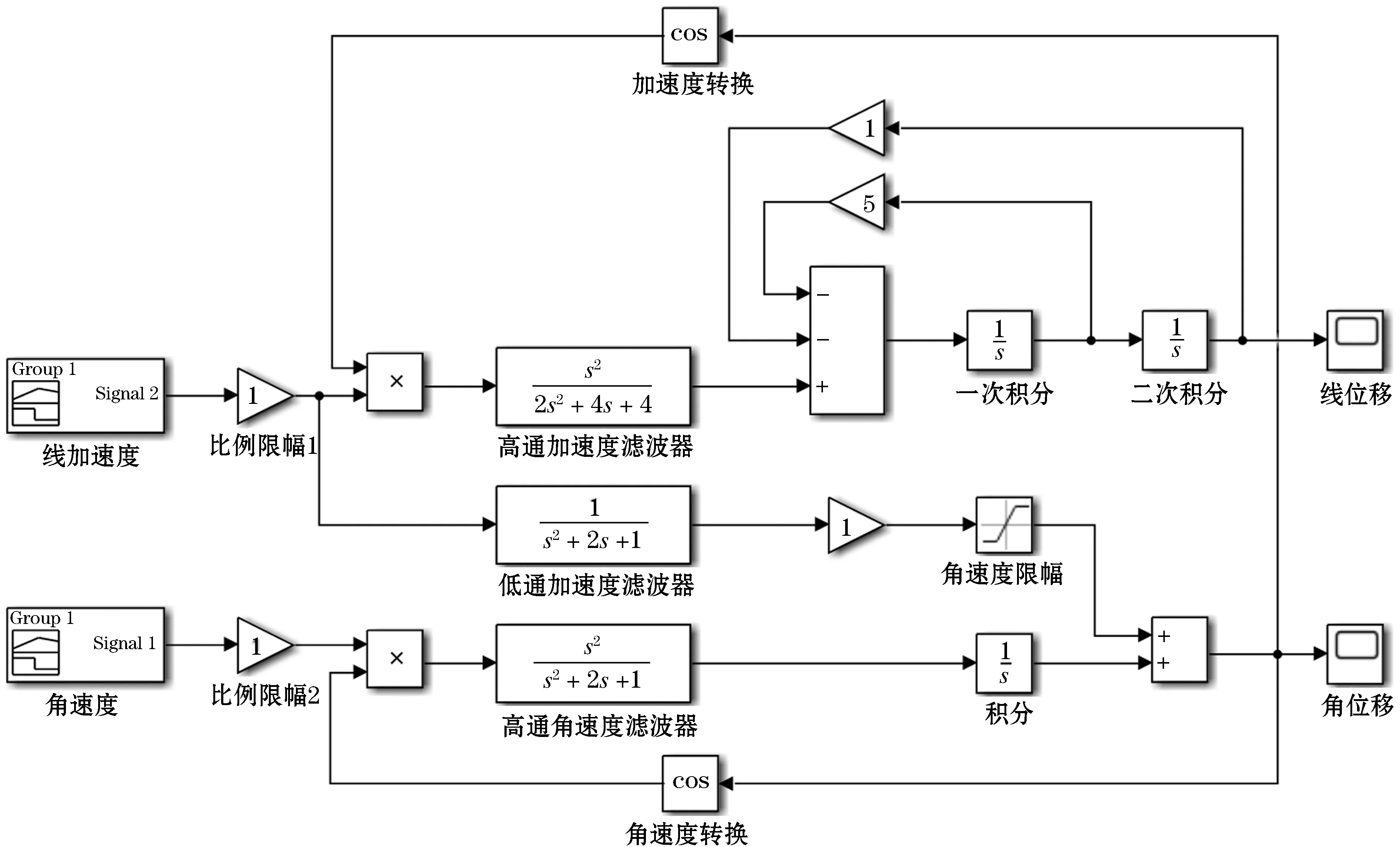
图6 洗出算法 Simulink仿真模拟Figure 6 Wash out algorithm Simulink simulation

在经典洗出算法中滤波器设计时，对设置的自然响应频率ω的选择非常重要，因此有必要进行多次调试并且在过程中找到合适的ω，这样不仅可以得到令人满意并且逼真度较高的模拟体验，还可以缩小平台的运动空间范围，节省资源[15].

关于针对平衡障碍的患者，多次重复的动感模拟运动对病情的康复是有益的[3]，各种模拟训练的康复动作会有所不同，例如攀登、蹦跳、加速奔跑等，具体的动作模拟过程还需要结合康复训练师的具体意见给出，这里采用输入加速度信号为1 m·s-2，持续时间为9 s，在10 s后回归至0，俯仰方向的角速度信号输入为0 rad/s，持续20 s.如图7、8所示，通过选取不同的滤波器参数分析洗出的效果.

图7 输入加速度信号Figure 7 Input acceleration signal

图8 输入角速度信号Figure 8 Input angular velocity signal

图9是经典洗出算Simulink仿真中使用不同自然响应频率参数的线加速度洗出结果图，三条曲线是自然响应频率ωah=1、ωah=2、ωah=3时的结果，阻尼系数ξah始终为1.从图9中可以看出三中不同自然响应频率都在10 s左右回到中立位置，并且位移范围都在±0.1 m内，但是绿色曲线位移最大红色曲线的位移最小，说明参数越大所需要的位移空间越小，越对平台有益.

图9 不同参数洗出角位移比较Figure 9 Comparison of angular displacement washed out by different parameters

由图10可以明显看出红色曲线角位移偏移过大，通过上文人体半规管模型可知，俯仰角速度不应该超过3.6°/s.因此自然响应频率参数过大会对模拟逼真程度有着负向的影响.因此这里调试阶段选用ωah=2的参数较为稳妥.

图10 不同参数洗出的角位移Figure 10 Angular displacements washed out by different parameters

3 联合仿真反解

洗出算法得到的是动平台的位移轨迹，而将洗出算法实践到康复机器人上，必须使驱动滑块完成响应运动才能使动平台做出洗出动作.因此本节采用ADAMS和Matlab联合仿真，反解出六滑块位移时间曲线.

3.1 ADAMS建模

首先需要将机械物理模型在ADAMS中建立，其方法使用Solidworks建模，在导出为.X_T文件，在ADAMS中打开并对其进行添加运动副.在导出模型时，应对模型的结构进行简化，只保留关键部分.其建模图形如图11、12所示.

图11 导入ADAMS的模型Figure 11 Import ADAMS 'model

图12 添加运动副后的模型Figure 12 Model after adding motion pair

3.2 建立Matlab机械系统模型

控制动平台的轨迹应对动平台质心直接进行添加点驱动，使其质心按照洗出算法得出的轨迹进行运动，从而模型中的滑块也会响应运动，从而可以反解出滑块的运动轨迹.这里使用ADAMS中插件Controls建立机械系统模型，结果见图13、14.

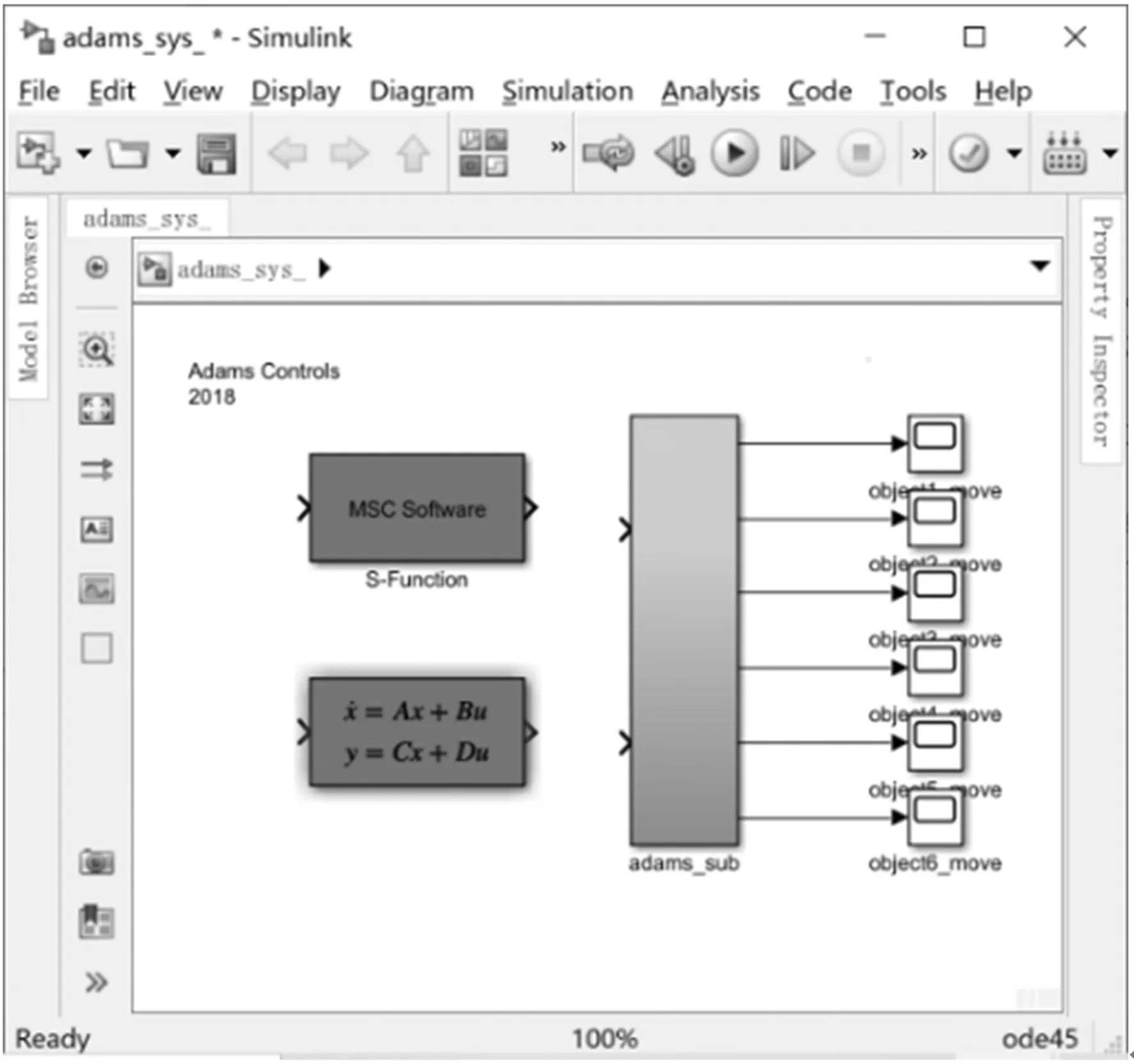
图13 6-PSS机器人机械系统模型Figure 13 6-PSS robot mechanical system model

图14 机械系统模型内部结构Figure 14 Internal structure of mechanical system model

3.3 联合仿真与结果分析

将机械系统模型与Simulink联合搭建仿真模拟如图15所示.

图15 联合仿真模拟总图Figure 15 General diagram of co-simulation

运行结果后得出六个滑块的位移轨迹如图16～21所示.

图16 滑块1位移曲线Figure 16 Displacement curve of slider 1

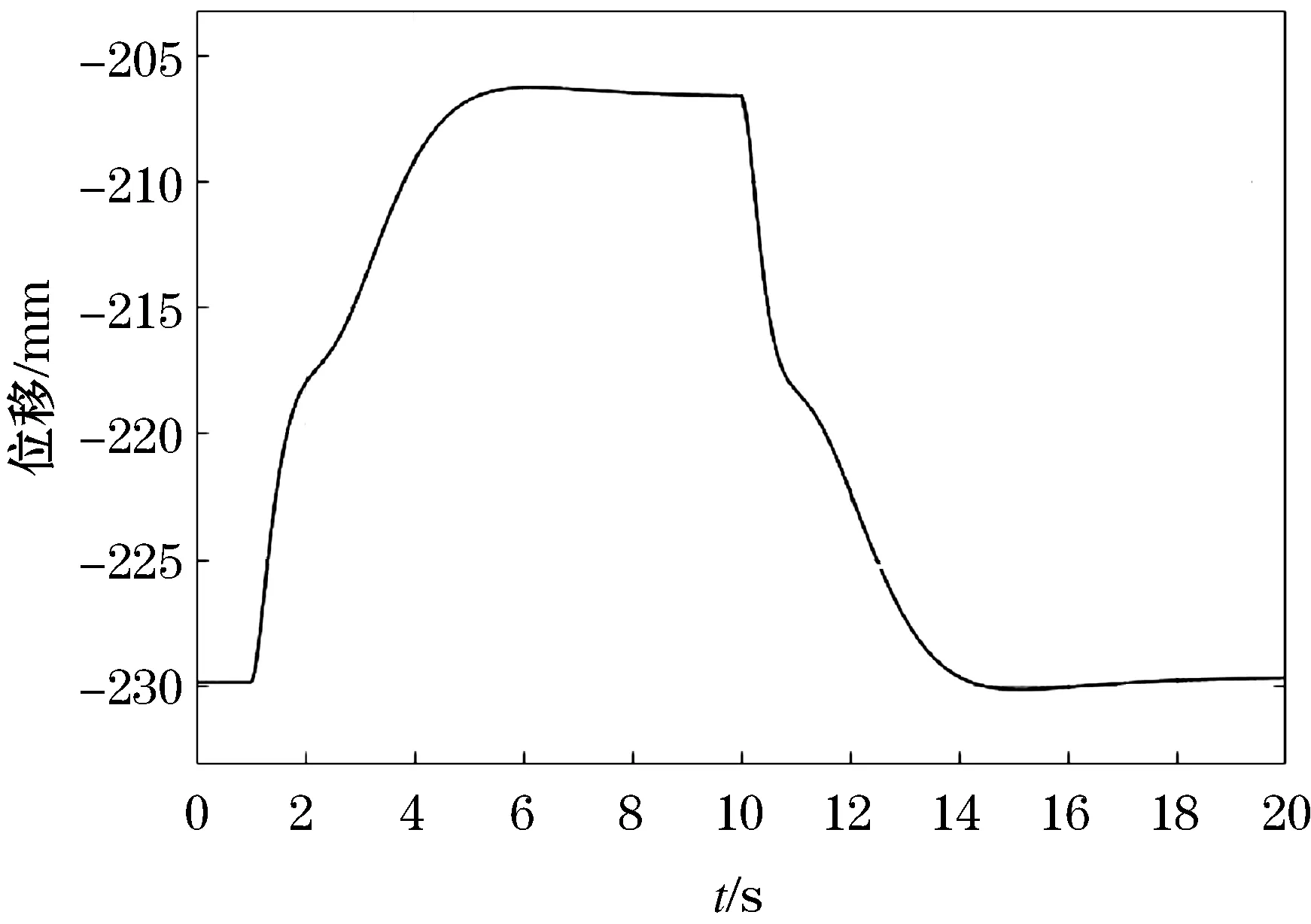
图17 滑块2位移曲线Figure 17 Displacement curve of slider 2

图18 滑块3位移曲线Figure 18 Displacement curve of slider 3

图19 滑块4位移曲线Figure 19 Displacement curve of slider 4

图20 滑块5位移曲线Figure 20 Displacement curve of slider 5

图21 滑块6位移曲线Figure 21 Displacement curve of slider 6

4 结 语

通过洗出算法洗出的动平台运动轨迹可以实现加速度的持续的效果，并且完成这次运动后，使得动平台回复到初始位置并且不会被人体感知，从而可以进行下一个运动的继续，连续不断的动作，就可以实现对康复病人前庭器官的运动感觉的刺激.

从本文的算法结论分析可以看出，在自然截止频率选择2时，更加适合洗出动作，算法结构精简，执行速度快，反馈速度也很快，但需要调节参数以达到理想效果.采用联合仿真的研究方法求出了6-PSS康复机器人的驱动轨迹，完成了康复机器人驱动部分的运动.此外，联合仿真在机器人反解这块也有一定研究价值，例如对焊接机器人的的运动反解.