长持时爆炸冲击波荷载作用下梁板组合结构的动力响应*
李圣童,汪 维,梁仕发,桑琴扬,郑荣跃
(1. 宁波大学土木与环境工程学院,浙江 宁波 315211;2. 宁波大学冲击与安全工程教育部重点实验室,浙江 宁波 315211;3. 军事科学院国防工程研究院,河南 洛阳 471023)
近年来,世界范围内因意外和恐怖袭击引起的爆炸事件频繁发生。爆炸不仅使建筑物发生破坏和倒塌,还对人类财产和社会稳定造成极大危害。钢筋混凝土梁板组合结构是建筑结构中重要的组成部分,对其开展在爆炸荷载作用下的动态响应和损伤状况研究,可为建筑物抗爆性能和整体安全提供参考依据。
爆炸载荷作用下,结构的应变率高达1 000 s或更高,钢筋和混凝土材料的强度明显提高,应力-应变关系变得更复杂,需要在材料模型中考虑非线性和应变速率效应等因素。目前,对钢筋混凝土板、梁的抗爆性能已有一定研究成果。阎石等将爆炸荷载作用下板的整体破坏模式分为弯曲破坏、剪切破坏和弯剪联合破坏;史祥生和贾敬尧等研究发现增加板厚、提高混凝土强度、增大钢筋直径、减少钢筋间距可以提高板的抗爆能力;李忠献等使用剩余承载力为指标评估构件破坏等级,提出一种简化确定钢筋混凝土板超压-冲量曲线的方法;张想柏等提出了震塌破坏系数,将近爆作用下钢筋混凝土板的典型破坏形态分为爆炸成坑、爆炸震塌、爆炸贯穿和爆炸冲切;Wang 等将接触爆炸作用下板的局部损伤划分为层裂、穿孔和冲孔失效;岳松林等推导了板的临界震塌厚度和临界贯穿厚度的计算公式;方秦等、柳锦春等发现不同爆炸冲击峰值作用下钢筋混凝土梁会发生弯曲、弯剪、斜剪以及直剪型等不同破坏形态;崔满通过实验探究了梁的裂缝开展、应变和位移变化情况,发现提高混凝土强度、增强箍筋用量可以提高梁的抗爆性能;汪维等通过近爆实验发现钢筋混凝土梁的破坏形态与爆高和比例距离有关;唐德高等研究发现使用高强钢筋可以提高大峰值爆炸荷载作用下梁变形恢复能力,降低位移峰值、裂缝长度和宽度。一些学者也进行了纤维材料加固后钢筋混凝土构件的动力响应和破坏机理分析。已有工作多为近爆或接触爆炸作用下对单独构件的研究,缺乏梁板组合结构整体抗爆性能的研究结果,对长持时远爆荷载作用下构件响应的研究深度不够。
为此,本文中,对长持时远场爆炸荷载作用下钢筋混凝土交叉梁板组合结构的毁伤特性和动态响应开展实验研究,分析组合结构的破坏模式。通过有限元软件Abaqus建立钢筋混凝土交叉梁板组合结构数值模型,将组合结构在爆炸荷载作用下的数值模拟结果与实验结果进行对比分析,使用挠跨比划分钢筋混凝土梁板组合结构的破坏模式。
1 实验设计
1.1 实验概况
采用激波管作为实验装置,对钢筋混凝土交叉梁板组合结构进行1 炮次模拟核武器爆炸冲击波加载作用。激波管能够模拟远场爆炸产生的爆炸冲击波,调整炸药质量、高压段充压和实验段长度可以控制爆炸冲击波的超压强度和持续时间。激波管由图1 所示4 个主要部分组成:(1)高压段,用于产生爆炸冲击波;(2)膜片和切割索,膜片用于保持高压段充压,切割索用于破坏膜片,使高压段和过渡段连通;(3)实验段,长度可以调整,通过过渡段与高压段连接;(4)端部框架,用于固定试件。

图1 实验装置示意图Fig. 1 Schematic diagram of the experimental device
钢筋混凝土梁板组合构件与外框采用C35 混凝土整体现浇。十字交叉梁截面尺寸为117 mm×200 mm(宽×高),受拉区配筋为6HPB300 ∅ 6,受压区配筋为4HPB300 ∅ 6,箍筋配筋为HPB300 ∅ 6@70。板尺寸为2 000 mm×2 000 mm×80 mm(长×宽×厚),板内放置HRB400∅ 12@200 双层双向钢筋。外框截面尺寸为250 mm×300 mm(宽×高),受拉区配筋为3HRB400 ∅ 20,受压区配筋为2HRB400 ∅ 14,箍筋配筋为HPB300∅ 8@100,浇筑时预留螺栓孔。组合构件尺寸及配筋示意图如图3 所示,钢筋保护层厚度均为15 mm。构件安装示意图如图2 所示。
图2 构件安装Fig. 2 Widget installation
实验前,在点爆源安装炸药,点爆源位置如图1 所示。炸药安装完成后密封人员出入口,对高压段充压至150.0 kPa。通过实验构件框架上预留的螺栓孔,采用高强钢构螺栓将实验件固定在实验段的末端。背爆面中心点位置采用一个量程为100 mm 的自动回弹位移传感器,型号为JWBS-100。在实验靶标框架顶部安装2 个的爆炸冲击瞬态压力测量传感器,用于测量作用在靶标上的冲击波超压,型号为CYG401,灵敏度温度系数为3×10FS/℃,位置如图3 所示。实验时,在0 ms利用电子延时起爆器同时起爆切割索和1、2 号点的炸药,同步启动测试系统,采集量测数据。
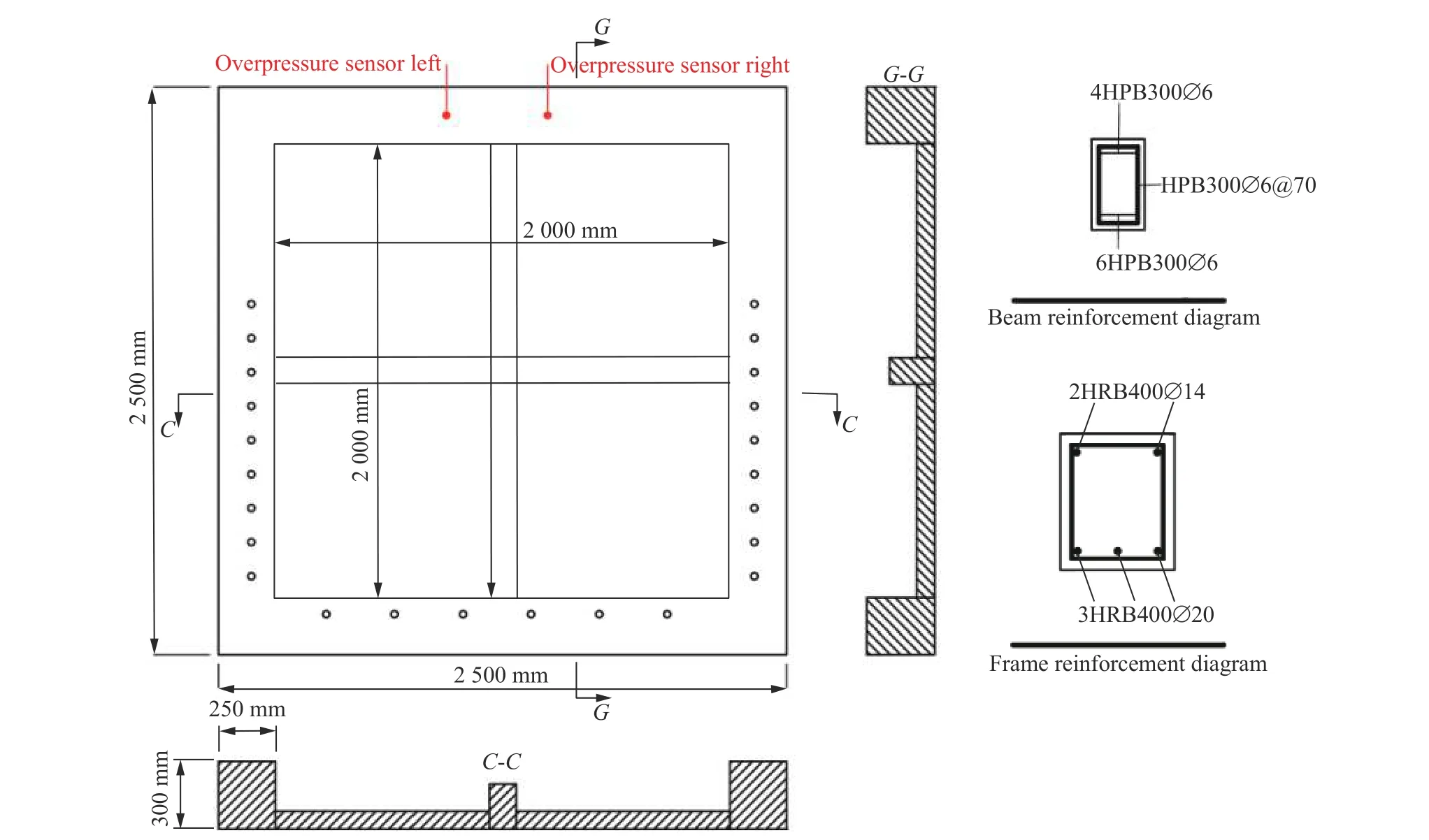
图3 梁板组合构件尺寸及配筋示意图Fig. 3 Dimensions and reinforcement of a beam-slab composite structure
1.2 实验结果与分析
实验测得的冲击波超压测试波形如图4 所示,组合结构背爆面中心点位移如图5 所示,实验后试件裂纹如图6 所示。由图4~6 可以看出,作用在靶标上的平均冲击波超压峰值为202.4 kPa,超压持续时间接近1 000 ms,组合结构背爆面中心最大位移为5.9 mm,实验后,组合结构背爆面出现多条宽约0.5 mm 的裂纹,组合构件处于轻微破坏状态,整体呈现弯曲破坏模式。在约76 ms 时,爆炸冲击波传递到了梁板组合构件上,在图中表现为冲击波超压突然上升,达到峰值,组合构件开始响应,此时组合构件中板和交叉梁共同工作。

图4 边框上冲击波超压测试波形Fig. 4 Shock wave overpressure waveforms measured on the frame

图5 组合结构背爆面中心点位移时程曲线Fig. 5 Displacement-time curve at the center point of the backside of the beam-slab composite structure

图6 实验后裂纹Fig. 6 Cracks after experiment
2 数值模拟
2.1 有限元模型建立
利用有限元软件Abaqus进行建模,板、梁、框尺寸及配筋与实验构件相同,有限元模型如图7 所示。混凝土为solid 六面体单元,单元类型为C3D8R,钢筋为truss 单元,单元类型为T3D2。采用embedded region 定义钢筋与混凝土的连接,取组合构件和框支座间的面定义面-面接触(surface to surface contact),边框的4 个侧面均设置为固定约束。在网格划分中,将混凝土部分网格尺寸设置为20 mm,钢筋部分网格尺寸设置为50 mm。

图7 数值计算模型Fig. 7 Numerical calculation models
2.2 材料模型
混凝土使用软件提供的混凝土塑性损伤(concrete damaged plasticity, CDP)模型,按《混凝土结构设计规范》规定,混凝土单轴受压的应力-应变关系为:


表1 混凝土材料模型参数[25-26]Table 1 Parameters of the concrete material model[25-26]
对钢筋材料采用双折线模型,其应力-应变本构关系为:

式中: σ为应力;为钢筋的弹性模量;ε为应变; σ为钢筋的屈服强度,其值按实际结构分析需要取标准值、设计值或平均值; ε为钢筋达到屈服强度时对应的应变; ε为钢筋极限强度对应的峰值应变。钢筋模型材料参数的取值如表2所示,表中 ρ为钢筋的密度,为钢筋弹性模量,为钢筋的直径,为钢筋的泊松比。

表2 钢筋材料模型参数[27]Table 2 Parameters of the steel material model[27]
2.3 模型验证
对图4 所示的2 个超压传感器的测量结果取均值后进行降噪滤波处理,使用该简化载荷对模型进行加载,如图8 所示,实验与数值模拟所得背爆面中心位移对比如图9 所示,实验后构件背爆面裂缝趋势和数值模拟对比如图10 所示,梁板组合结构在长持时爆炸荷载作用下破坏过程如图11 所示。从图9~11 可以看出,组合构件背爆面裂纹和中心点位移峰值的计算结果与实验结果吻合较好,本研究采用的数值模拟能够较好地展示钢筋混凝土梁板组合构件在爆炸荷载作用下的开裂、裂纹传播和混凝土破坏等过程,可用于研究梁板组合构件在爆炸载荷作用下的破坏形态和动态力学性能。

图8 简化加载曲线Fig. 8 Simplified loading curves

图9 背爆面中心点位移时程曲线Fig. 9 Displacement-time curves at the center point of the backside

图10 实验和数值模拟得到的裂缝Fig. 10 Experimental and simulated cracks
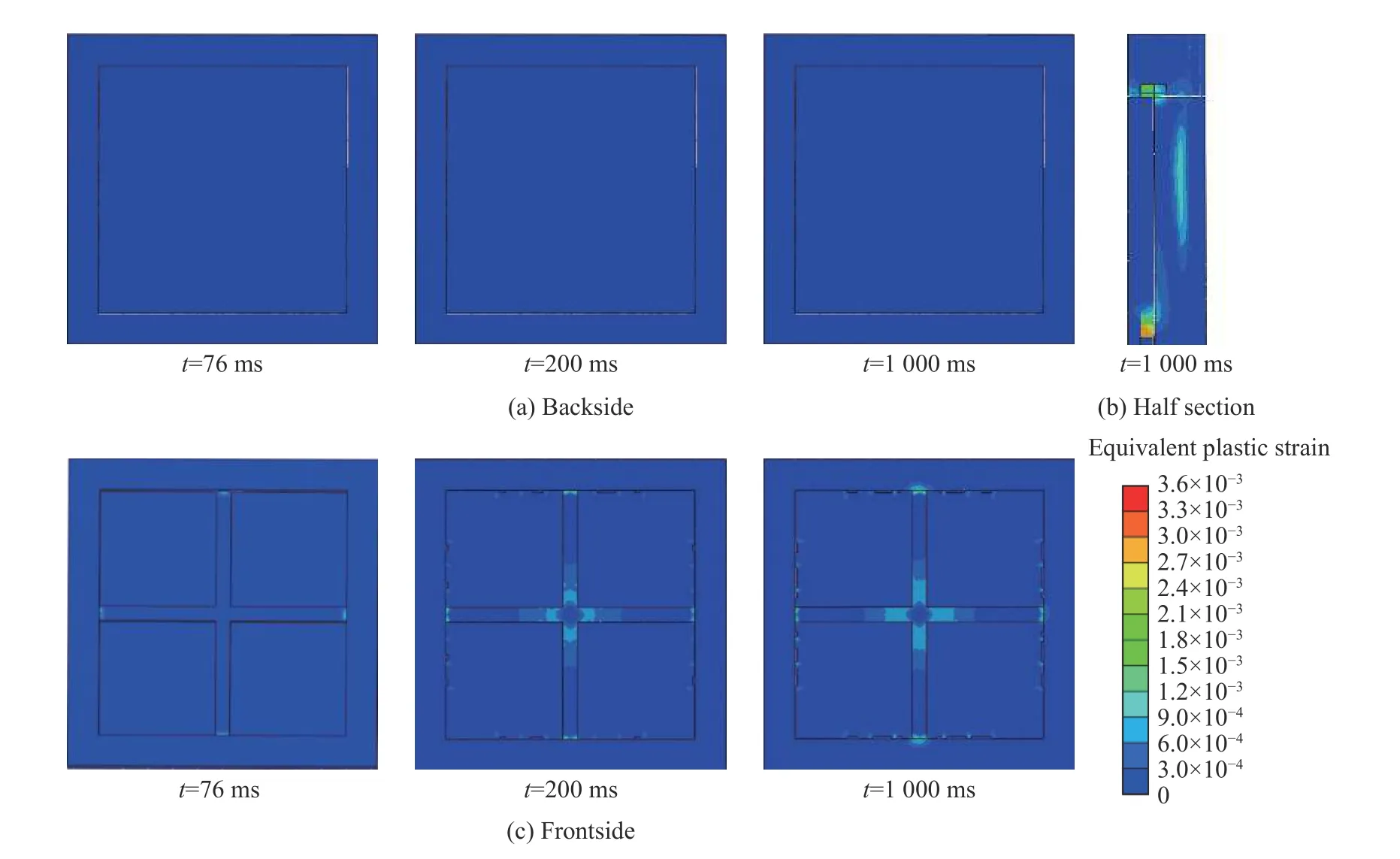
图11 简化爆炸冲击波载荷下结构的破坏过程Fig. 11 Failure process of the structure under simplified explosion shock wave loading
由图9 可以看出,在0~76 ms 时段,实验和数值模拟所得位移曲线的变化趋势几乎一致,二者峰值十分接近;实验位移曲线在220~1 000 ms 时段振动趋于零,数值模拟位移曲线在200~1 000 ms 时段振动趋近于4.0 mm;与数值模拟相比,实验背爆面中心点位移响应滞后约20 ms。爆后,实验和数值模拟的裂纹发展相似,但残余位移存在约4.2 mm 的差别,这是因为:(1)现浇钢筋混凝土梁板组合试件为非均匀介质,存在初始缺陷,而数值模拟中使用的材料模型十分理想,导致实验与数值模拟结果不同;(2)建模使用的钢筋与混凝土constrain-embedded region 约束的滑移与构件实际情况不同,造成差异;(3)在数值模拟中,背爆面的混凝土单元发生开裂损伤,单元损伤后弹性模量降低,导致回弹数值偏低。
由图11 可以看出,在76 ms 时,爆炸冲击波传递至梁板组合构件,迎爆面的框支座连接处、梁板连接处以及背爆面的混凝土发生轻微破坏;在200 ms 时,构件迎爆面破坏发展至框支座连接处混凝土部分破坏、十字梁1/2 跨度内应变较大,但交叉梁中心混凝土完整,且板与框支座连接处应变较大处位置分布与板中心处底层钢筋布置位置接近;到1 000 ms 时,组合整体呈现弯曲破坏,背爆面出现多条裂纹,裂纹主要沿对角线分布,背爆面中心最大位移5.9 mm,组合构件处于轻微破坏状态。
3 分析与讨论
3.1 破坏模式分析
结合钢筋混凝土板和钢筋混凝土梁的破坏模式,在相同实验冲量(=50 000 kPa·ms)、不同峰值爆炸荷载作用下对梁板组合结构的破坏模式进行研究。采用简化三角形爆炸压力时程曲线对梁板组合结构进行加载,模拟时,使用多组冲量相同、荷载峰值不同的简化爆炸荷载时程曲线对组合构件进行加载。取其中具有代表性的4 组工况,荷载峰值分别为200.0、208.3、217.4 和222.2 kPa,对应的加载时间t分别为500、480、460 和450 ms,简化加载曲线如图12所示;在长持时、冲量相同、峰值不同的爆炸冲击荷载作用下梁板组合构件典型破坏如图13 所示,为发生该破坏对应的时刻。

图12 简化三角形加载曲线Fig. 12 Simplified triangle load curves
数值模拟结果表明,在峰值为200.0 kPa 的简化爆炸荷载作用下,梁板组合结构迎爆面框支座连接处混凝土破坏,背爆面中心板与十字梁交叉部分连接处发生少量混凝土剥落,组合结构发生轻微弯曲破坏,如图13(a)所示。
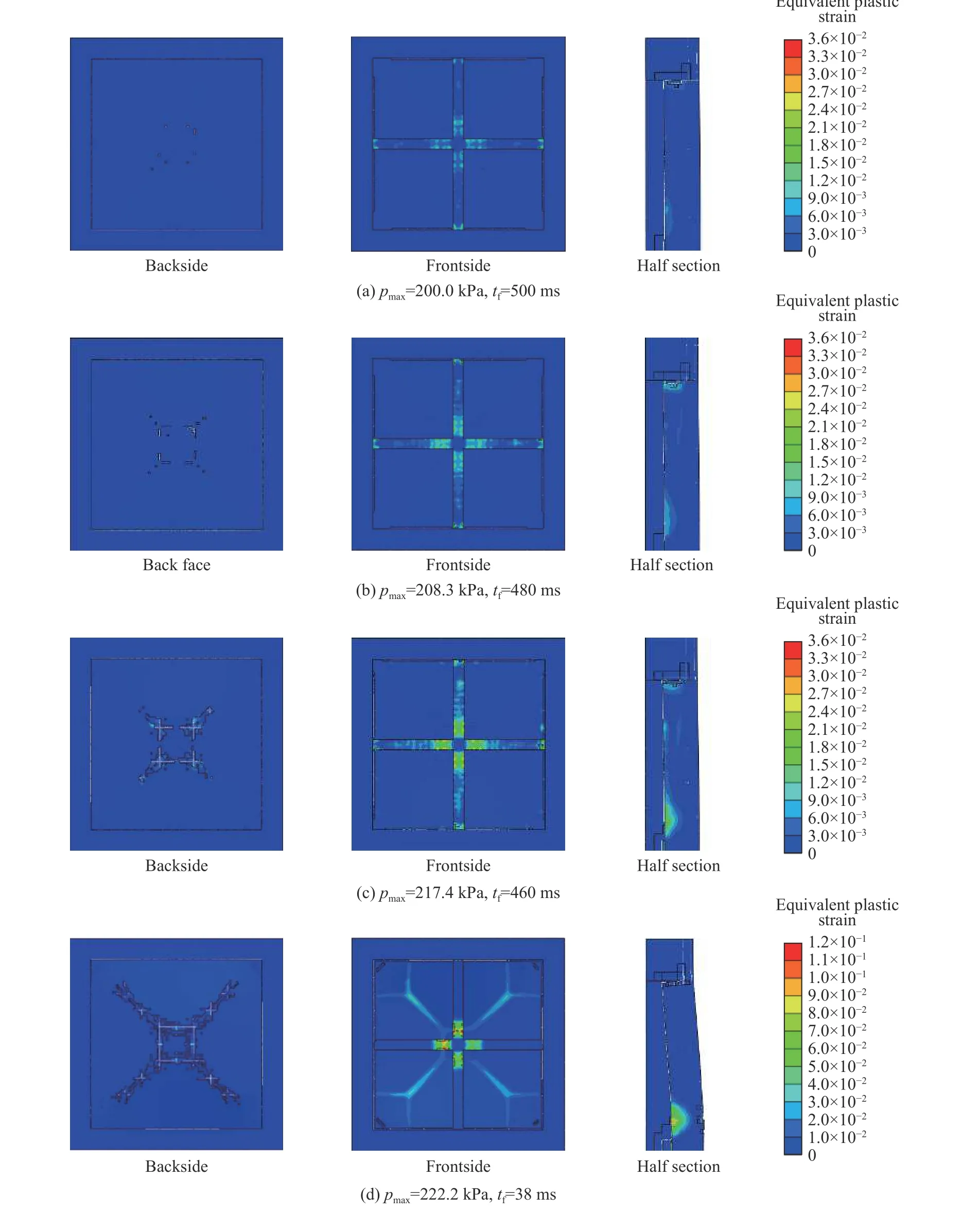
图13 不同工况下构件背爆面、迎爆面以及半剖面的破坏Fig. 13 Failure in the backsides, frontsides and half sections of the structures under different load conditions
在峰值为208.3 kPa 的简化爆炸荷载作用下,组合结构迎爆面与框支座连接处混凝土破坏程度继续增加,背爆面中心发生混凝土层裂剥落,部分钢筋裸露,剥落部分与板中心处底层钢筋分布十分接近,沿对角线向外延伸,十字梁部分未发生混凝土剥落,组合构件发生弯剪组合破坏,如图13(b)所示。
在峰值为217.4kPa 的简化爆炸荷载作用下,迎爆面组合结构与框支座的连接处、十字梁混凝土破坏区域扩大,此时组合构件破坏程度加重、混凝土剥落量增加、支座连接处钢筋裸露,背爆面中心部分混凝土破坏沿对角线发展且层裂加深,此时板底层钢筋裸露面积增加,组合构件整体呈现弯剪组合破坏,板与交叉梁丧失共同工作能力,如图13(c)所示。
在峰值为222.2 kPa 的简化爆炸荷载作用下,加载至38 ms 时,组合构件突然在支座连接处呈现混凝土冲切破坏,加载至450 ms 时,组合构件板部分混凝土背爆面崩塌破碎区域与迎爆面压碎区域贯穿,钢筋弯曲变形,梁部分在迎爆面中心交叉部分旁的混凝土呈现冲切破坏,在背爆面近交叉梁中心3/5 处均存在混凝土破坏剥落,残余混凝土厚度为30~40 mm,组合构件发生冲切破坏,丧失承载力,如图13(d)所示。
图14 为不同工况的背爆面中心点位移峰值对比图,图15 为不同工况的背爆面中心点位移曲线。由图14、图15 可以看出,相同冲量作用下,随着加载峰值的提高,组合构件背爆面中心点位移峰值增加。在峰值为200.0、208.3 和217.4 kPa 的简化爆炸冲击波加载作用下,组合构件背爆面中心点位移发展至最大位移值之前曲线斜率一致,达到最大值之后均呈现振动回弹下降趋势;而峰值为222.2 kPa 的简化爆炸冲击波加载作用下,组合构件突然毫无征兆地发生破坏并丧失承载力。随着长持时爆炸荷载峰值的提高,梁板组合结构从构件发生轻微弯曲破坏,过渡到支座处混凝土破坏、背爆面混凝土层裂剥落、钢筋弯曲裸露的弯剪联合破坏,最终发展成短时间内框支座处冲切破坏,背爆面板部分混凝土贯穿破坏、钢筋裸露并弯曲变形,此时交叉梁部分跨中附近混凝土破坏、钢筋弯曲变形,构件完全丧失承载力。

图14 不同工况下背爆面中心点的位移峰值Fig. 14 Displacement peaks of the central point of the backside under different load conditions
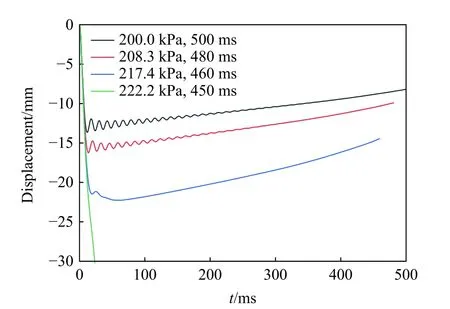
图15 不同工况下背爆面中心点的位移时程曲线Fig. 15 Displacement-time curves of the central point of the backside under different load conditions
3.2 破坏等级划分
为了进行长持时爆炸荷载作用下梁板组合构件毁伤的等级划分,结合实验和数值模拟对背爆面中心点处的位移曲线进行了测量和统计,统计结果如表3 所示。其中,构件2 的数值模拟使用实验波形加载曲线,构件3~11 的数值模拟使用三角形简化加载曲线。根据统计结果和结构的毁伤程度,以中心点处的位移挠跨比、组合构件的破坏表现作为划分标准,将不同工况下组合结构伤划分为轻度破坏、中度破坏、重度破坏和完全破坏。轻度破坏的表现形式是梁板组合结构的迎爆面支座处出现少量混凝土脱落,背爆面仅出现小裂纹,没有明显的混凝土破坏,挠跨比≤0.5%;中度破坏的表现为梁板组合构件迎爆面中心弯曲凹陷,支座连接处混凝土破坏加深,背爆面混凝土开始剥落,随加载峰值的增加,剥落沿板中心处底层钢筋布置发展,构件主要为弯曲破坏,挠跨比0.5%<≤1.0%;重度破坏的主要表现是组合构件支座处混凝土破坏,板背爆面混凝土沿对角线破坏剥落,钢筋变形并裸露,交叉梁背爆面混凝土中心四侧破坏,钢筋弯曲变形,组合构件总体呈现弯剪联合破坏,挠跨比1.0%<≤1.5%;完全破坏的破坏特征为组合构件突然发生破坏,板部分混凝土整体破坏贯穿、钢筋完全裸露变形,交叉梁背爆面中心外侧均有混凝土崩塌剥落现象,组合构件完全丧失承载能力,挠跨比>1.5%。
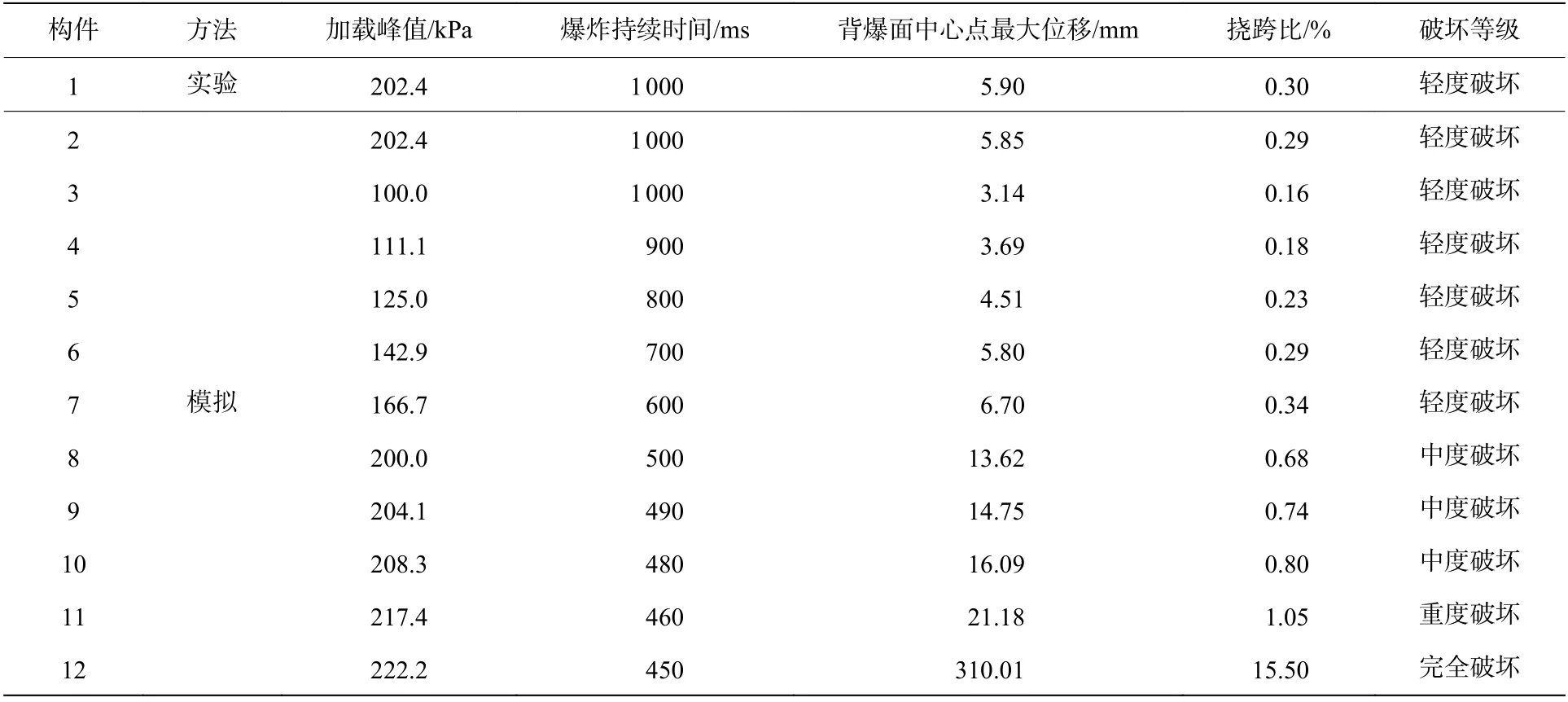
表3 相同冲量作用下梁板组合构件的破坏等级划分Table 3 Failure grade classification of beam-slab composite structures under the same impulse
4 结 论
设计并进行了长持时爆炸冲击波荷载作用下梁板组合结构的实验,结合有限元软件建立了数值模型,并将模拟结果与实验结果进行了比较,验证了模型的可行性。在此基础上,分析了长持时爆炸荷载加载强度对构件抗爆性能的影响,得出以下结论。
(1)本文中建立的数值模型可以对结构破坏的动态演变过程进行可视化再现,数值模拟计算结果与实验结果的毁伤相似度较高、背爆面中心点的位移峰值接近,证实了该数值模型及算法的有效性。
(2)相同冲量作用下,随着长持时爆炸荷载峰值的提高,梁板组合结构从整体轻微弯曲破坏,过渡到弯剪联合破坏,最终发展至短时间内构件冲切破坏;组合构件中,板部分破坏早于交叉梁部分,当板部分混凝土整体贯穿破坏时,组合构件丧失共同承载力。
(3)本次实验的钢筋混凝土梁板组合结构的破坏等级划分和相应的破坏模式为:挠跨比≤0.5%时,轻微破坏,构件能够正常使用;当0.5%<≤1.0% 时,中度破坏,稍微维修后可继续正常使用;当1.0%<≤1.5%时,重度破坏,较大维修后可继续使用;当>1.5%时,完全破坏,组合构件完全丧失承载能力。
应注意的是,本文中建立的破坏等级划分是依据本次实验的少量实验数据建立的,建立的判据仅适用于本次实验的钢筋混凝土梁板组合构件,对其他形式组合构件的毁伤判据需要在以后进一步研究。文中的数据可为钢筋混凝土梁板组合结构的抗爆研究与设计提供实验结果,也为后续的钢筋混凝土建筑物整体毁伤评估奠定基础。

