基于混合射线追踪的矿井电磁波分析方法
孙继平,张高敏
(中国矿业大学(北京) 机电与信息工程学院,北京 100083)
无线通信技术和装备在煤矿安全生产中发挥着重要作用,是煤矿智能化的关键技术和装备。电磁波在空间受限的矿井巷道内为多径传播,无线通信设备天线(以下简称天线)的安装位置和巷道内电磁波能量分布密切相关,发射天线在巷道内不同位置辐射出的电磁波具有不同的衰减规律。为保障巷道内车辆和行人正常通行、提高灾害事故发生后无线通信系统的可靠性,天线一般安装在顶板或巷帮附近,因此需要研究适用于收发天线位于顶板或巷帮附近时矿井电磁波的分析方法及电磁波传播特性,用来指导天线安装,优化天线位置,在无线通信设备的发射功率和接收灵敏度不变的前提下,提高无线传输距离、信号稳定性和可靠性。
射线追踪法把高频电磁波作为光波射线,计算出发射点和接收点之间的有效传播路径,并根据路径长度和反射点处的反射系数计算目标位置的电场强度,不需要大的计算机内存和算力就可以在较大的三维空间仿真电磁波传播,被广泛用于研究矿井受限空间内的电磁波传播特性。文献[7]在弯曲巷道内测量并用射线追踪法仿真了人体对无线通信信道的影响,研究了电磁波的多径色散,提出了一种基于弯曲巷道场景下广义路径损耗模型。文献[8]把半圆拱形顶面分割成多个满足射线追踪法中的镜像原理所需的有效反射截面并建立各截面的平面方程,研究了电磁波在半圆拱形巷道内的传播特性。文献[9]研究了壁面粗糙度对隧道无线电传播的影响,提出了一种统一的射线追踪和模态方法来模拟粗糙壁面隧道的电磁波传播,证明了射线追踪法与模态法在分析粗糙壁面隧道内远场电磁波特性时存在等价性。文献[10]用几何光学法模拟铁路隧道曲率、隧道壁的粗糙度,结合波模理论提出了一种射线波模混合方法研究在公路和铁路实际隧道中电磁波的传播特性。文献[12]使用几何光学模型和波模理论提出一种多模态模型研究电磁波在矿井巷道内的电磁波衰减,并将多模态模型与阴影衰落模型相结合,把多模态模型推广到房柱式采煤区。上述理论模型和测量试验研究重点是提高预测电磁波在巷道内传播损耗的精度,多把收发点设置在巷道横截面中心附近,较少考虑收发点靠近顶板或巷帮时电磁波的损耗。文献[5]测量了收发天线在煤矿巷道内同一高度不同水平位置的接收信号强度,分析了收发天线沿巷道水平方向上变化时接收信号强度的变化规律,但缺少理论分析。文献[13]在仿真矩形巷道内用多波模理论推导了发射天线的耦合效率和方向函数,仿真了发射天线在巷道横截面不同位置上和波模的耦合效率及其辐射场分布,但没有考虑收发天线之间的距离变化和波模耦合效率之间的关系。文献[14]中的一个场景测量了收发天线等高并固定在同一侧巷帮时接收信号强度和数据包接收速率之间的关系,此时最大有效通信距离小于收发天线位于巷道截面中心时的一半,缺少收发天线位置和电磁波传播特性之间的理论分析。
当前文献多数研究收发天线在巷道截面中心附近区域时电磁波传播特性,较少分析收发天线靠近顶板或巷帮附近时的电磁波传播特性。发射天线在巷道中不同位置激发出的电磁波信号能量分布不同,不同接收位置接收到的信号强度也不相同。用射线追踪法仿真收发天线同时靠近巷帮附近时,发现收发天线越靠近巷帮,接收信号能量越高,与电磁波传播理论及测量结果矛盾,表明传统射线追踪法不适合研究收发天线同时靠近巷帮附近时的电场波传播特性。提出了修正射线追踪模型,确立了收发天线在巷帮或巷帮与顶板交接线上时有效射线的判定方法和反射点的入射能量的计算方法,提高了传统射线法在收发天线靠近顶板或巷帮附近时预测接收信号强度的精度。在修正射线追踪模型和测量数据的基础上,提出混合射线追踪法,进一步扩大了射线追踪法研究矿井电磁波传播特性的适用范围。
1 射线追踪法
1.1 基本原理
基于几何光学理论的射线追踪法因计算简单精确度高被广泛用于研究矿井电磁波传播特性。该方法将发射天线辐射出的电磁波当作平面波,以光射线形式不断向外辐射能量,通过统计发射天线到接收天线的全部射线路径长度,计算出总的路径损耗和反射损耗,进而预测电磁波在巷道内的传播特性。图1用矩形巷道的俯视图说明射线追踪法基本原理。
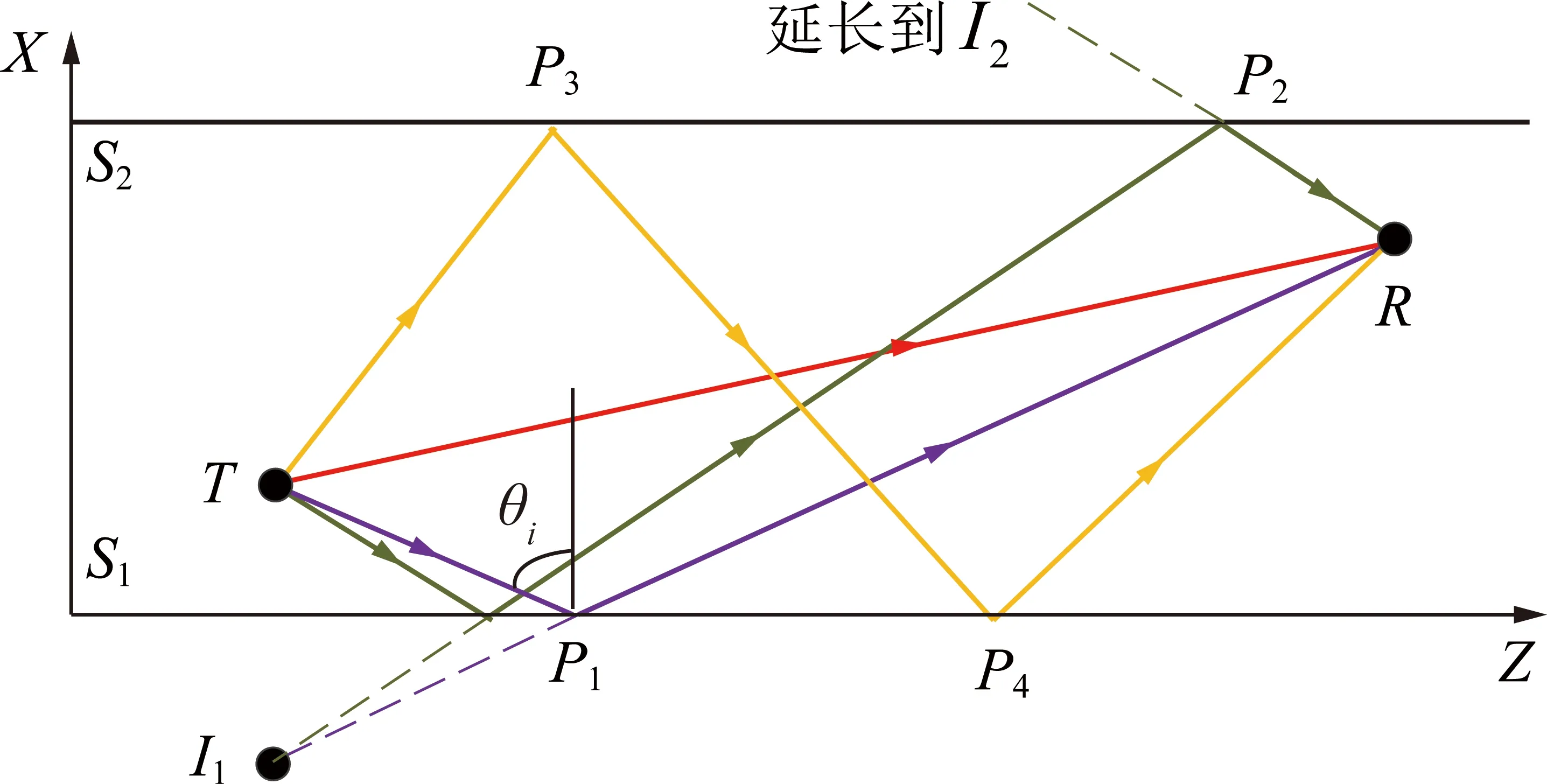
图1 射线追踪法原理Fig.1 Principle of the ray tracing
图1中,和分别为发射点和接收点,作发射点关于反射面的镜像点,连接和可得与反射面的交点,即反射面上的反射点,组成一条一次反射路径,组成一条二次反射路径;为射线入射到反射面的入射角;为发射点关于反射面的二次镜像点;和为二次入射射线在反射面上的反射点;为二次入射射线在反射面上的反射点。设入射点电场为,则接收点电场为
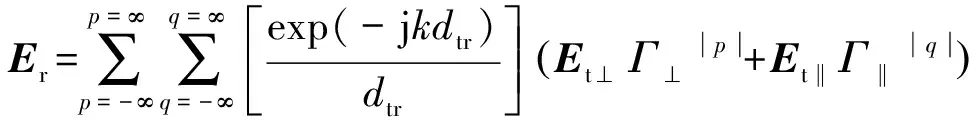
(1)
式中,j为虚数单位;为电磁波波数;和分别为垂直极化波和水平极化波的反射次数,镜像点位于轴负侧为负号,位于轴正侧时为正号;为发射点和接收点之间的距离;和为入射波电场矢量分解为垂直极化和水平极化的电场矢量;和为垂直极化波和水平极化波的反射系数。
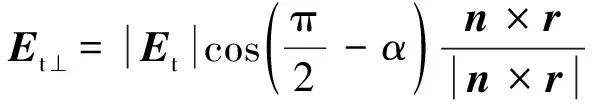
(2)

(3)
式中,为反射点所在平面法向量;为入射波方向矢量;为入射波电场矢量和反射面的夹角。
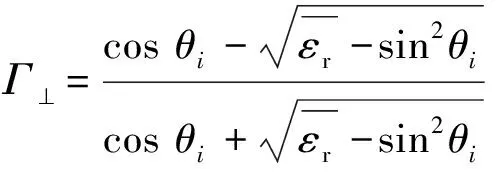
(4)
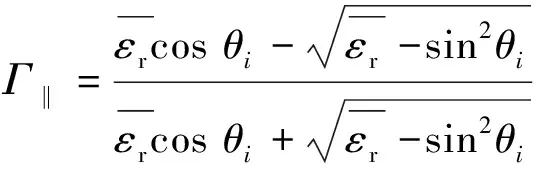
(5)
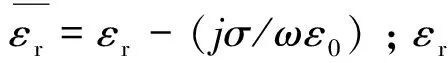
1.2 射线追踪法误差分析
用射线追踪法研究矿井电磁波传播特性时,若发射点和入射点在巷道截面中心及中心附近区域,此时发射点到4个壁面上各个反射点的入射角相差不大,且受巷道内物理环境因素影响较小,大量文献也证明该方法在巷道中心及其附近可以较为准确的预测巷道内电磁波传播特性。然而,当发射点和接收点都离开巷道截面中心,同时贴近巷道同一侧巷帮或同一侧顶板时,射线追踪法计算出的接收点电磁波能量和真实值之间的误差将会显著增大。下面在三维矩形巷道内用4个壁面的一次有效反射射线给予证明。
设矩形巷道宽为,高为,用,,,表示顶底板和巷帮,如图2所示。发射点和接收点在巷道内高度为2,沿巷道纵向收发点之间的距离为,到巷帮的初始距离都为。根据射线追踪法原理可知,经一次反射到达,在4个壁面的反射点分别为,,和,得到4条到的有效路径。为巷道横截面,4个一次反射点都在上,中心到和的距离都为2,各个反射点处对应的入射角分别为,,和,可得各入射角为
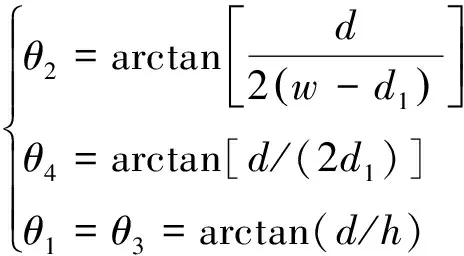
(6)
因为反射系数和入射角有关,可以对式(4)和(5)中的求导,得出反射系数随的变化率:
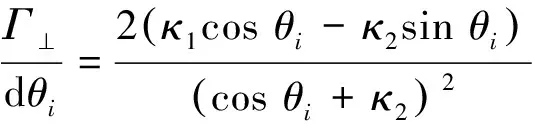
(7)

(8)
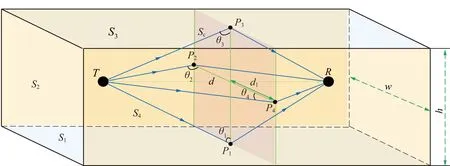
图2 射线追踪法一次反射路径Fig.2 One reflection path of the ray tracing
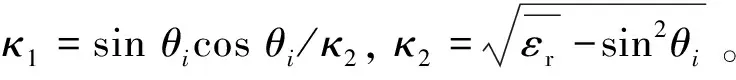
图3 反射系数变化率Fig.3 Gradient of reflection coeffficent
根据式(2)和(3)可知收发天线方向不变时,两者仅在水平方向移动,和的大小不变。根据式(6)可知到的距离不变时,和与收发天线到巷帮的距离有关,和与收发天线的高度有关。当收发天线在水平方向向巷帮同时移动Δ(Δ为收发天线在水平方向上向巷帮移动的一段距离),则和为
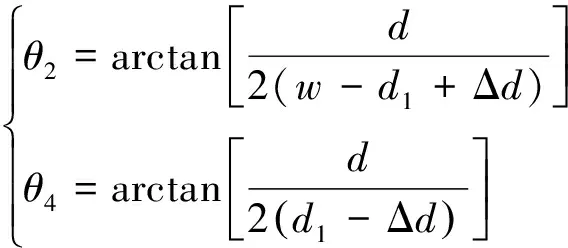
(9)
因此,当收发天线高度不变,水平方向变化引起接收点电场能量变化的根本原因是和发生变化。当Δ趋近于,即收发天线同时趋近于同一侧巷帮时,减小,增大并趋近于90°,<。而2种极化波反射系数的变化率和入射角成正比,所以引起反射系数的增大量大于引起的减小量,导致收发天线越靠近巷帮,接收信号电场强度越大。
在宽4.80 m、高3.40 m、长300 m的矩形巷道内,巷道壁相对介电常数为5,归一化发射点的初始发射能量,沿巷道水平方向间隔0.01 m采样,沿巷道纵向方向间隔1 m采样,收发点相距20,60,120,150,300 m水平采样点的相对接收信号强度以及1~300 m内在各水平采样点的平均相对接收信号强度仿真结果如图4所示。
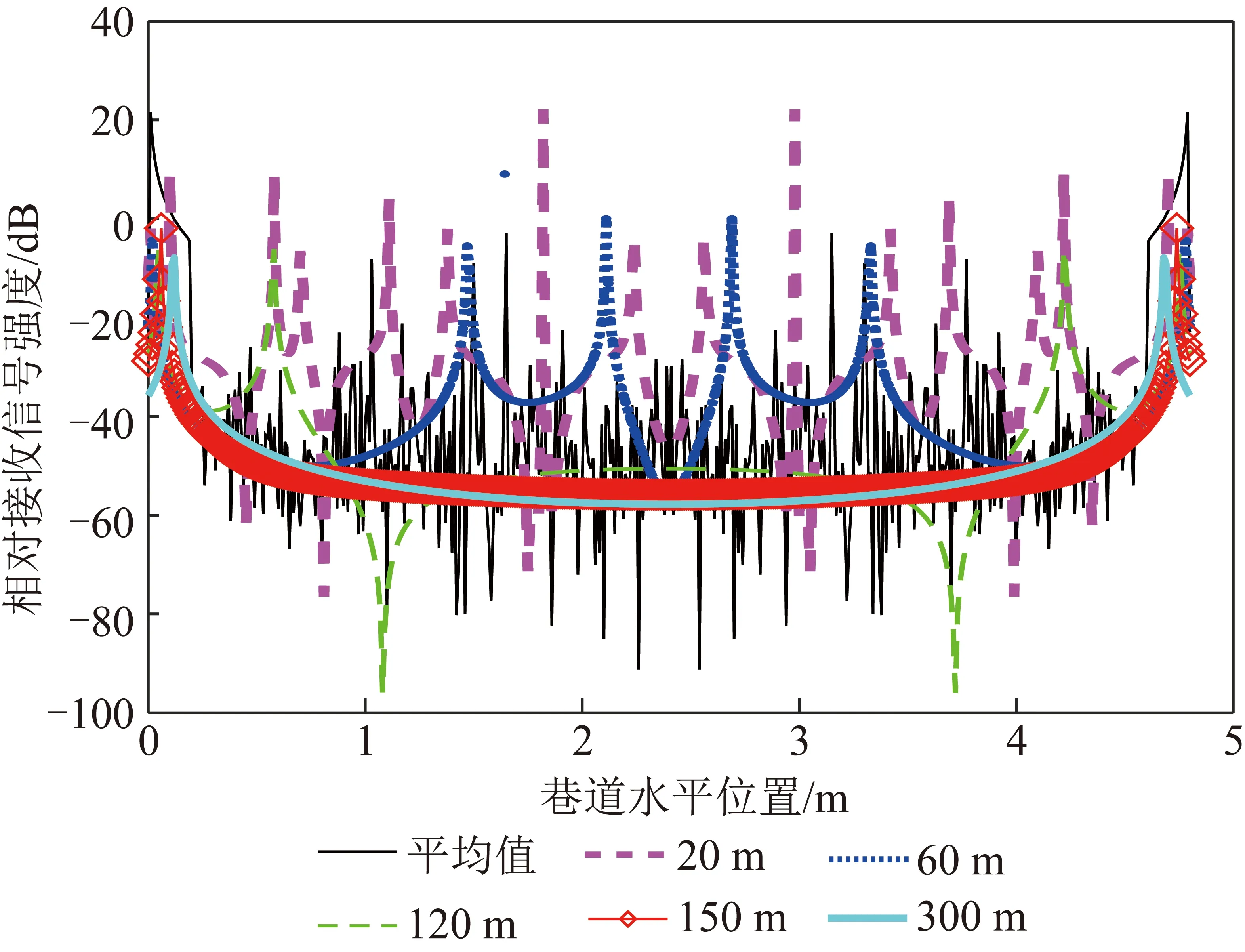
图4 收发点沿巷道水平方向的相对信号强度Fig.4 Relative signal strength of the transceiver point along the horizontal direction of tunnel
由仿真结果可知在实际环境中,收发天线之间距离较近时,接收信号强度沿巷道水平方向上呈周期变化,随着收发天线之间的距离增加,周期越来越大。根据1~300 m内在巷道水平方向上平均相对接收信号强度变化可知,收发天线位置越靠近巷帮,接收到的信号强度越高。进一步推理,射线追踪法可以计算出当发射天线和接收天线都在巷帮和顶板的夹角处接收到的电磁波信号强度最大,此时电磁波有效传输距离最远。显然该结论和波导理论与实际测量结果相矛盾,在收发天线都在巷帮附近时用传统射线追踪法预测的接收信号强度会有较大误差。
2 修正射线追踪模型
2.1 有效射线判定
传统射线追踪法没有考虑收发天线在巷帮附近时有效射线的判定,计算出的接收信号强度大于在巷道中心区域的接收信号强度。巷道内从发送点到接收点之间存在无穷多条反射路径,随着反射次数增加反射损耗也会快速增加,经过多次反射后到达接收点的有效射线对接收点处电场强度的贡献率较小,只需考虑发射点发出的经过1次反射、2次反射和3次反射后能够到达接收点的射线。
对于矩形巷道,理论上存在4条1次反射路径、12条2次反射路径、36条3次反射路径,但实际能够到达接收点的有效路径和发射点接收点的位置有关,特别是发射点或接收点位于顶板或巷帮交界上、发射点和接收点在同一顶板或巷帮时,需要计算反射点和收发点是否在同一平面,否则会把沿平面传播的反射路径作为有效反射路径,导致计算出收发点同时在巷帮附近的接收信号强度较大。
改进后的有效射线的判定方法考虑了收发点在巷道某一壁面或两壁面交线上的特殊位置情况,计算过程如下:
(1)首先判断发射点是否位于巷道四周某一平面(=1,2,3,4)内。若是则只需求关于其余3个面(=1,2,3,4且≠)的镜像点,否则分别求在4个面的镜像点。
(2)计算镜像点与接收点组成的矢量m同面的反射点1,若1同时位于2个平面的交线上或巷道顶底板及巷帮的实际有效区域内,则此次反射线路径无效,直接返回发射点开始计算下一条反射路径,否则计算镜像点关于下一平面的二级像点。
(3)从发射点经过面上的反射点到接收点的路径即为一条有效反射路径。
2.2 反射点入射能量修正
到达反射点的电磁波可以分解为垂直极化波和水平极化波,由式(1)可知,射线追踪法计算出的接收点电场强度和收发点之间的距离、入射角、垂直极化波和水平极化波的电场强度以及2种极化波各自的反射次数有关,并且每一个反射点都使用同一个电场强度,缺少分析每一个反射点处入射电场能量的变化情况,同样也没有考虑最后一个反射点到接收点之间只有传播损耗,不存在反射损耗的情况,在此予以修正。
以图1中二次反射路径为例,推导反射点入射电场能量的修正方法。
(1)发射点的初始电场作为入射电场分解为垂直极化电场和水平极化电场:即=+,到达反射点时电场为传播距离衰减后的值:
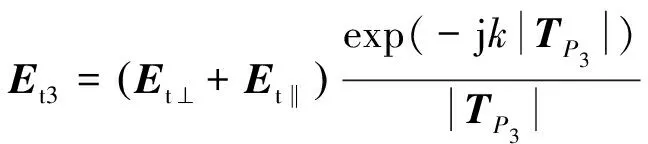
(10)
经过反射点后的反射电场为
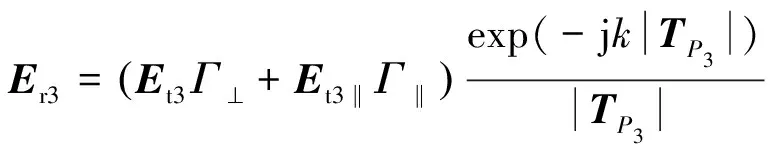
(11)
(2)到达反射点的电场为传播|3|距离衰减后的值:
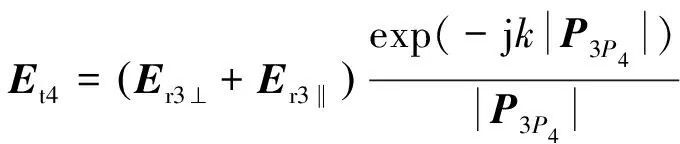
(12)
经过反射点后的反射电场为
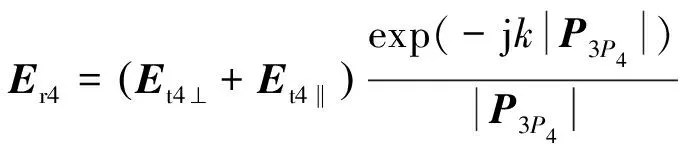
(13)
(3)到达接收点的电场为传播|4|距离衰减后的值:

(14)
从入射点直射到接收点的电场为
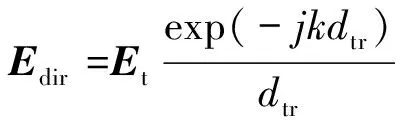
(15)
式中,为发射点到接收点之间直射射线路径长度。
修正后从发射点到接收点全部有效反射射线电场为
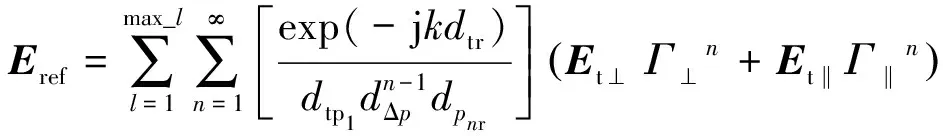
(16)
式中,为任意一条有效反射路径的最大反射次数;为有效反射路径数量;max_为最大有效反射路径数量;tp为任意一条路径中从发射点到第1个反射点之间的射线长度;Δ为2个反射点之间的射线长度;r为最后一个反射点到接收点之间的射线长度。
不考虑直射路径,只考虑反射路径,通过对比式(1)和式(16)也可以发现传统射线追踪法计算出的接收电场强度要大于修正射线追踪模型计算出的接收电场强度。对传统射线追踪法修正后,从发射点到接收点的全部有效射线包括直射路径和反射路径,故由直射电场能量(式(15))和反射电场总能量(式(16))可得修正射线追踪模型:
=+
(17)
传统射线追踪法和修正射线追踪模型的直射路径计算方法相同,主要修正了电磁波在反射路径中的计算方法。以宽度为4.80 m、高为3.70 m、长300 m的等效矩形巷道为研究对象,电磁波从发射点在4个巷道壁面上经过一次反射到达接收点,发射点和接收点沿巷道水平方向间隔0.01 m采样,沿巷道纵向从1~300 m间隔1 m采样,传统射线追踪法和修正射线追踪模型计算出巷道水平方向平均相对接收信号强度如图5所示。因为修正射线追踪模型考虑了到达每个反射点之前的路径损耗、入射能量,计算出的接收信号强度比传统射线追踪法计算出的结果波动要小,并且扩大了收发天线沿巷道水平方向上射线追踪法的适用范围,但是在收发点到巷帮的距离在0~0.30 m或4.50~4.80 m内,不管是传统射线追踪法和修正射线追踪法,收发天线越靠近巷帮,电磁波信号的相对接收信号强度越大。进一步表明射线追踪法适用于研究发射天线和接收天线位于巷道截面大部分区域内矿井电磁波的传播特性,不适合研究发射点和接收点同时靠近同一侧巷帮或顶板时矿井电磁波的传播特性。
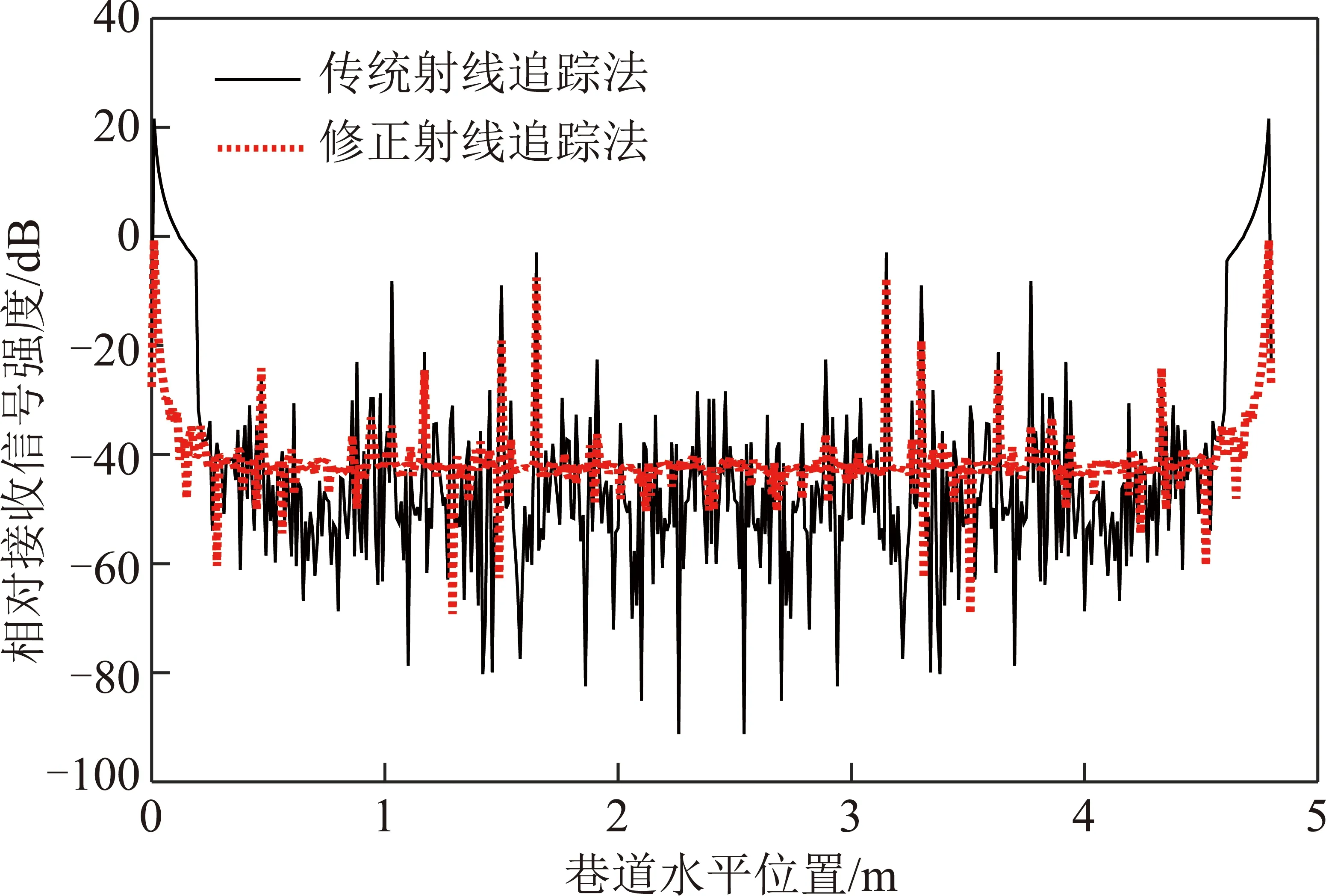
图5 巷道水平方向平均相对接收信号强度Fig.5 Average relative received signal strength in the horizontal direction of the tunnel
3 混合射线追踪模型
3.1 位置衰减系数
位置衰减系数表示发射点和接收点到巷帮或顶板的距离同电磁波场强的关系。水平位置衰减系数定义:发射点和接收点位于巷道截面内同一高度(相等),同时沿巷道截面水平()方向变化,计算在处实际测量电磁波信号功率值和射线追踪法计算出仿真值的差值,该差值经过拟合后得到的电磁波信号功率和水平位置之间的关系表达式。
在巷道截面竖直()方向上的竖直位置衰减系数定义和水平位置衰减系数相似。文献[4,9,12]研究了天线位置对巷道截面电磁波信号能量分布的影响,得出天线位置仅影响巷道截面电磁波信号能量分布,和电磁波沿巷道纵向传播衰减关系不大,但没有研究水平方向不同天线位置与电磁波信号强度之间的关系。为减少统计误差,实际用于计算位置衰减系数的测量值和仿真值为各纵向采样点的平均值。水平位置衰减系数的表达式为
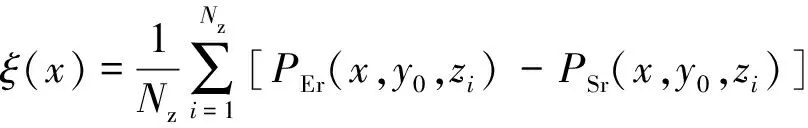
(18)
式中,为采样点的测量值;为采样点的仿真值;为天线已知高度;为集合中元素的个数,∈,为采样点沿巷道纵向坐标的集合。
水平位置衰减系数为包含接收点水平位置信息的电场的功率,将位置衰减系数和修正射线追踪法求得的接收点信号强度相加可得用分贝表示的水平方向混合射线追踪模型:
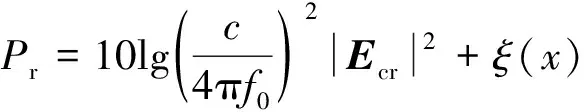
(19)
式中,为接收点的信号强度;为电磁波的载波频率;为修正射线追踪模型中的接收点信号的电场;为光速。
3.2 测量试验
测量环境为双马煤矿的辅运大巷。辅运大巷横截面为马蹄形,最宽处5.20 m,最高处4.00 m,整个巷道壁喷射混凝土,底板相对平整。巷道一侧中部有输水管道和通风管道,顶部有动力和通信电缆,为减少纵向导体对电磁波的影响,在巷道无纵向导体的一侧完成天线位置测量,测量设备和巷道环境如图6所示。

图6 测量设备和巷道环境Fig.6 Measuring equipment and the tunnel environment
测量时发射和接收天线都采用1 dBi的全向偶极子垂直极化天线,设备发射功率1 W,发射和接收天线等高1.70 m,载波频率为580 MHz ,收发天线在巷道截面中心最大通信距离为530 m,紧贴巷帮时最大通信距离为150 m。由于巷道内存在大量反射路径,并且在发射点近场还存在多波模相互干扰,需要在收发天线距离较近时增加采样密度。距发射天线较远时将呈现波导效应,信号强度变化趋于平缓,采样点可以相对稀疏。
根据对现有矿井电磁波理论和多次测量结果的分析,沿巷道纵向到发射天线分别为1,2,4,8,16,30,50,80,120,150 m处作为纵向采样点。同样发射天线和接收天线在水平位置靠近巷帮时电场变化激烈,远离巷帮时电场变化相对平缓,在发射和接收设备天线同时到巷帮的距离为0,0.01,0.04,0.10,0.30,0.60,1.20和2.40 m处采样。
采样时发射设备天线保持静止状态,接收设备天线从纵向采样起始位置依次移动到最后一个采样点,信号稳定后在每个测量点测20次取平均值作为该采样点的最终接收信号强度。
3.3 混合射线追踪模型推导
单纯的理论模型受巷道内动力和通信电缆、压风管、水管、铁轨、架空线等纵向导体、巷道壁面粗糙度等影响较大,会增加理论模型和测量数据之间的误差,建立和实际巷道近似匹配的数学模型复杂度高,几乎无法实现。实际巷道沿纵向存在一定的弯曲度,并且巷帮上固定有指示牌等障碍物,若收发天线靠近巷帮,两天线之间不存在有效直射路径,在仿真建模时无法模拟真实巷道场景。因此,在相同巷道参数下,用仿真值和测量值计算出收发天线在巷道水平方向或竖直方向上的位置衰减系数,将射线追踪理论和测量试验相结合,统计收发天线在巷帮附近时的衰减规律,推导出理论和试验相结合的混合射线追踪模型可以扩大射线追踪法研究矿井电磁波的适用范围,提高预测精度。
测量环境为马蹄形巷道,可以通过面积等效为矩形巷道,本次测量的马蹄形巷道横截面如图7所示。用等效面积方法可以把该巷道等价为宽4.80 m、高3.40 m的矩形巷道,巷道的竖直和水平壁面的相对介电常数为5。
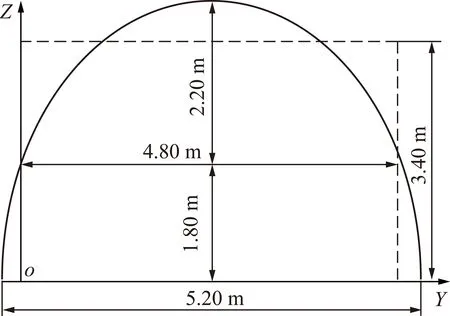
图7 巷道等效参数Fig.7 Equivalent parameters of the tunnel
表1中列出发射和接收天线在巷道内各水平采样点沿纵向1~150 m内测量的电场强度和基于修正射线追踪模型得到的相同采样点仿真值之间的差值。

表1 采样点信号强度测量值和仿真值的差值Table 1 Difference between the measured and theoretical value of signal power at sampling points
根据表1中的收发天线在不同位置处接收信号功率实测值和仿真值之间的差值,使用线性回归来计算水平位置衰减系数。最小二乘法是线性回归方法中的一种数据拟合优化方法,根据测量值和预测值之间的最小误差计算出最佳匹配函数,满足预测数据和实测数据之间误差的平方和最小,因此本文使用最小二乘法多项式拟合收发天线水平位置和接收信号强度之间的线性方程。使用最小二乘法求解位置衰减系数和水平位置之间的函数关系为

(20)
其中,为待求多项式的系数;为多项式的阶数;为收发天线到同一侧巷帮的距离。对式(20)向量化得
=
(21)
=[…]

=[…]
式中,为采样点的个数;为第个采样点的接收信号强度。
用最小二乘法求解可得
=()
(22)
拟合次数越高,拟合结果越精确,但公式复杂度越高,并且样本数据的微小变动都会导致公式剧烈变化,通过多次试验确定拟合次数为3,此时,确定系数()为0.967,可以满足实际需求。最终得到的水平位置衰减系数(dB)为
()=1437-5914+708-3049
(23)
图8给出了收发天线从紧贴巷帮水平移动到巷道中心位置时的水平位置衰减系数变化趋势。收发天线在巷道截面中心(2.40 m)和1/8(0.60 m)的水平范围内,位置衰减系数平均为6.8 dB,天线水平位置变化对信号功率影响不大。当天线到巷帮距离为0.20 m时位置衰减系数约为20 dB,到巷帮距离为0.10 m时该系数为26 dB,到巷帮距离为0.01 m时该系数为30 dB,对应0.20 m到0.10 m和0.10 m到0.01 m的位置衰减系数变化率分别为60 dB/m和45 dB/m。分析表明收发天线在巷道中心区域电磁波信号强度变化平缓,靠近巷帮时电磁波能量衰减迅速增大,电磁波在这2个区域的衰减规律极为不同。
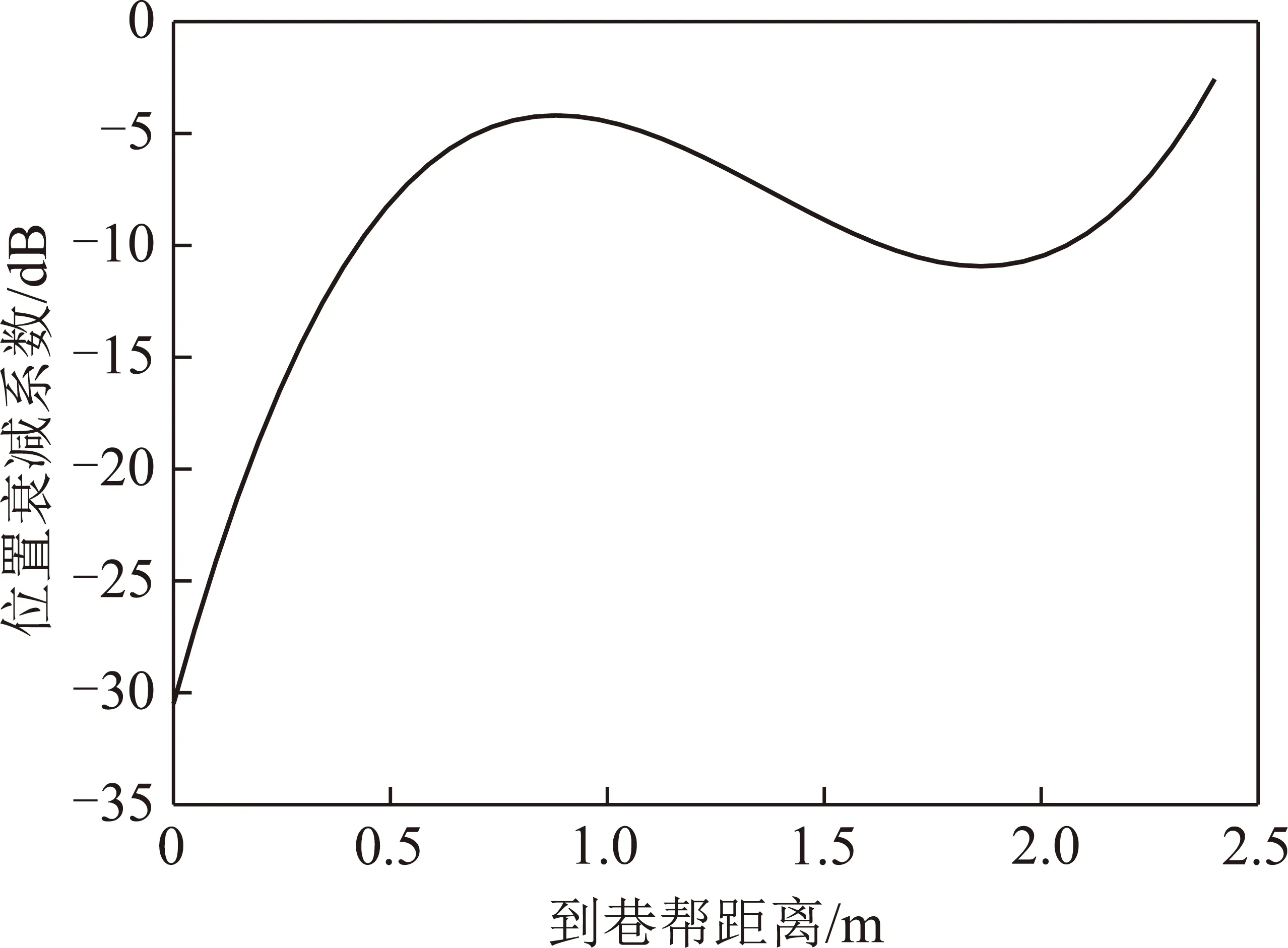
图8 水平位置衰减系数变化趋势Fig.8 Variation trend of the horizontal position attenuation coefficient
把包含收发天线水平位置和电磁波衰减特性的位置衰减系数代入式(19)可得完整的混合射线追踪法的矿井电磁波传播模型:
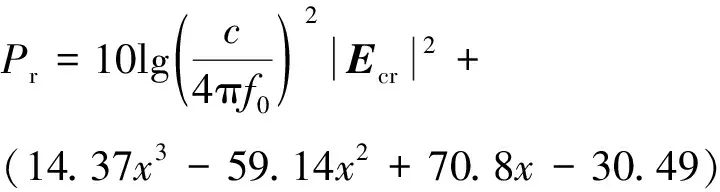
(24)
4 结果分析
根据第3节混合射线追踪模型中的巷道参数,传统射线追踪法、修正射线追踪模型、混合射线追踪模型经过3次反射后的仿真结果和矿井下实际测量结果如图9所示。
收发天线位于巷道水平中心2.40 m以及1.20 m处,传统射线追踪法的仿真值和实际测量值在沿巷道纵向1~150 m的范围内平均误差都在10 dB以内,此区域约为巷道宽的1/4。相同误差条件下,修正射线追踪模型能够计算出收发天线同时到巷帮0.60 m时电磁波的功率,相比传统射线追踪法在水平方向适用范围提高了25%。收发天线离巷帮越近,2种方法的仿真值和测量值之间的差值越大,在0~0.30 m范围2种射线追踪法的仿真值结果趋于一致,但平均高于测量值25 dB。对于混合射线追踪模型,在相同仿真条件下收发天线在巷道中心和到巷帮1.20 m处的仿真值和测量值误差增大了2 dB,收发天线距巷帮0.10 m时,由原来的21 dB变为2 dB;收发天线距巷帮0.04 m时,由原来的26 dB变为1 dB;收发天线紧贴巷帮时,由原来的33 dB变为4 dB。在收发天线靠近巷帮0.01 m和0 m的极限条件下,混合射线追踪模型比传统射线追踪法和修正射线追踪模型的预测精度分别提高了8.5倍和7.3倍。混合射线追踪模型和测量值在巷道截面内各水平采样点的平均误差均小于5 dB,不管收发天线位于巷道中心还是巷帮附近,仿真值和测量值都能较好的匹配。

图9 3种射线追踪模型仿真和测量结果Fig.9 Result of three ray tracing simulation and measurement
5 结 论
(1)射线追踪法可用于研究收发天线在巷道截面中心附近时矿井电磁波的传播特性,当收发天线同时到同一侧巷帮的距离小于1/4倍巷道宽度时,仿真误差逐渐增大,且与收发天线到巷帮的距离成反比。从理论上证明了射线追踪法不适于研究收发天线同时靠近同一侧巷帮时矿井电磁波的传播特性。
(2)在射线追踪法的基础上,提出修正射线追踪模型,改进了收发天线位于巷帮上或巷帮与顶板边界上时有效反射路径的判定方法和优化各反射点处入射电场强度与接收电场强度的计算方法,在巷道截面中心区域比传统射线追踪法提高了25%的适用范围,但当收发天线到巷帮距离小于0.60 m时,和测量值相比误差依然较大。
(3)提出位置衰减系数,根据测量值和修正射线追踪模型的仿真值,推导出巷道水平位置衰减系数,得出收发天线在巷道中心区域电磁波信号强度变化平缓,靠近巷帮时电磁波能量衰减迅速增大。
(4)在修正射线追踪模型和位置衰减系数的基础上,提出了混合射线追踪模型,该模型在整个巷道水平范围内仿真值和测量值之间的纵向平均误差均小于5 dB,进一步扩大了射线追踪法的适用范围。

