考虑分布式光伏与储能联合的区域电网电压稳定性控制方法
孙永辉, 赵树野, 张秀路, 韩永强, 张海瑞
(1.国网内蒙古东部电力有限公司经济技术研究院, 内蒙古 呼和浩特 010010; 2.沈阳工业大学, 辽宁 沈阳110870)
0 引言
大量分布式电源及储能等分布式电源接入区域电网,对系统电压稳定性控制提出挑战。 在传统配电系统运行中,电力潮流大多是从高压侧流向低压侧的单向潮流。 分布式储能的接入使得储能系统中产生了双向潮流,从而对传统的电压调节造成一定干扰[1]~[3]。 在可再生能源并网过程中,光伏电站出力的波动性和不确定性增加了区域电网电压的波动性,对区域电网的电压稳定性造成了一定的冲击。
为提高区域电网电压稳定性,国内外专家对分布式储能进行了大量研究。 文献[4]提出了在分布式光储系统中,基于储能单元控制的一种分布式储能控制方法。 通过对分布式储能的荷电状态分析, 采用合理的充放电顺序控制蓄电池充放电,实现区域电网中分布式储能的能量平衡。 文献[5]提出了一种基于信息快速提取的分布式控制方案,其操作过程中信息传输量较少,不需要高带宽通信系统。 文献[6]提出了一种基于电力共享单元的优化控制方法,实现混合微电网结构中的电能传输优化管理。 文献[7]基于下垂控制的电压频率控制方法, 使分布式电源及分布式储能出力平衡达到较高要求。 文献[8]提出了一种改进的下垂控制策略,通过设计合理的虚拟阻抗,分析线路阻抗对电压的影响, 将分布式储能及分布式电源的出力电压恢复到额定值。 以上研究主要针对的是光伏电站与分布式储能并网逆变器控制,而对于区域型多能源系统的光储协调优化控制研究较少。
本文通过确定分布式储能与光伏电站的协调配合机理,判断分布式储能的荷电状态;基于可再生能源出力不确定性, 提出了一种分布式储能与光伏电站协调运行方法, 并建立基于Markov 链储能的协调控制模型。 该方法可平抑光伏电站出力的不确定性, 提升区域电网电压的稳定性。
1 光储系统电压模型
1.1 分布式光储系统节点电压模型
随着光伏发电并网容量的不断增加,区域电网电压稳定性受到的不确定性冲击也随之增加[9]~[11]。 为解决光伏电站的出力波动性及不确定性对区域电网电压造成的冲击问题,本文针对分布式光伏与储能联合区域电网电压的控制方法进行研究。 分布式光伏与储能联合系统如图1所示。

图1 分布式光储联合系统Fig.1 Distributed energy storage access system diagram
为了提升光储系统的电压稳定性水平,在图1 所示区域光储联合系统中的节点j 处配置一定容量的分布式储能系统, 分别对节点j 处投入或未投入储能的电压进行分析。 为有效分析各节点处的电压值,在区域系统中没有配置分布式储能时,相邻节点处的电压关系为

式中:Plj为区域电网中节点j 处负荷消耗的有功功率;Qlj为区域电网中节点j 处负荷消耗的无功功率;Pcsj为区域电网中节点j 处光储系统发出的额定有功功率;Qcsj为区域电网中节点j 处光储系统发出的额定无功功率。
1.2 基于分布式储能的电网电压稳定模型
在分布式储能系统中, 当系统无分布式光伏储能接入时,系统受不确定性影响因素较少,其中各节 点的电 压满足[12]~[14]:
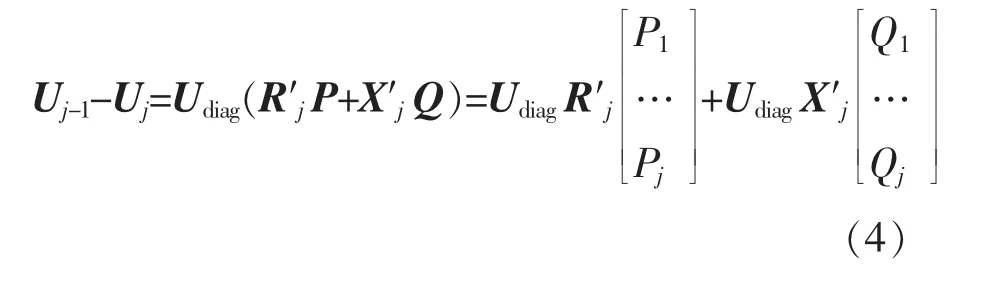
式中:Uj为系统中各个节点处电压有效值向量,Uj-1=[U0,…,Uj-1]T,Uj=[U0,…,Uj-1,Uj]T,Uj-1,Uj为区域系统中相邻两线路的节点电压有效值;U 为区域电网中所有相邻节点间的电阻矩阵,U=[1/Uj,…,1/Uj-1,1/Uj]T;R 为区域电网中所有相邻节点间的电阻矩阵,R=[R1,…,Rj-1,Rj]T;Xj为区域电网中所有相邻节点的电抗矩阵,Xj=[X1, …,Xj-1,Xj]T;Udiag为矩阵U 中的对角矩阵;R′j为矩阵Rj中的对角矩阵;X′j为矩阵Xj的对角矩阵;P 为区域电力系统中各节点所需的有功功率列向量,P=[P1,…,Pj-1,Pj]T;Q 为区域电力系统中各节点所需的无功功率列向量,Q=[Q1,…,Qj-1,Qj]T。
分布式储能装置充电时, 与电网内负荷具有相同的有功无功需求特性。 当分布式储能装置放电时,具有与光伏电站相似的输出特性。充放电过程中系统的潮流方向相反。 区域电网的各节点电压方程为
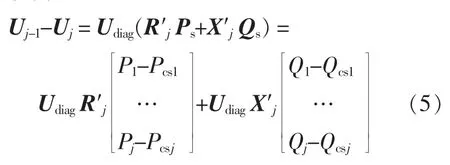
式中:Pcsj为区域电网中节点j 处分布式储能装置输出的有功功率;Qcsj为区域电网中节点j 处分布式储能装置的无功输出功率;Ps为区域电网中所有分布式储能装置输出有功功率的列向量;Qs为区域电网中所有分布式储能装置输出无功功率的列向量。
储能装置对电网电压稳定的支撑作用表示为
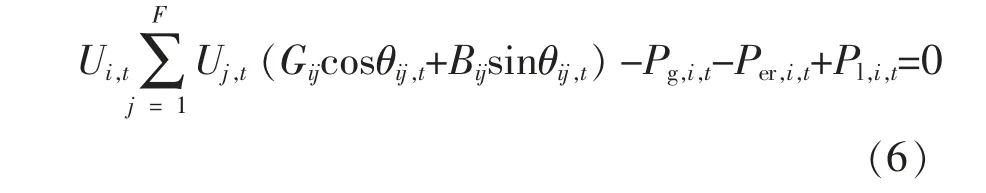
式中: 下标g,er,l 分别表示在复合储能系统中同步发电机的输出功率、储能交换功率和负荷功率;Ui,t,Uj,t分 别 为t 时 段 节 点i,j 处 的 节 点 电 压;Gij为节点i,j 间的线路电导;Bij为节点i,j 间的线路电纳;θij,t为t 时段节点i,j 处电压的相角差。
1.3 光储协调控制模型
为解决区域电网中光伏出力波动导致系统产生的电压波动问题,采用基于Markov 链储能模型对光伏储能系统充放电循环进行建模。 首先计算光伏储能系统为电网负载供电的概率, 进而评估使光伏发电达到可用性水平的最佳储能规模。
设S 为所有分布式光伏源的集合, 若Xi为第i 个PV 源提供的功率, 则PV 源提供的总功率Xr为

式中:L 为区域电网中系统的负荷及所需储能电池功率的总和。
光伏电站的发电可用性应大于所需负载的可用性。当光伏组件是唯一的发电源设备时,如果没有储能装置的参与, 就无法满足区域电网电能的可用性。
使用Markov 链模型将可用性和存储容量进行关联,建立如图2 所示的模型。
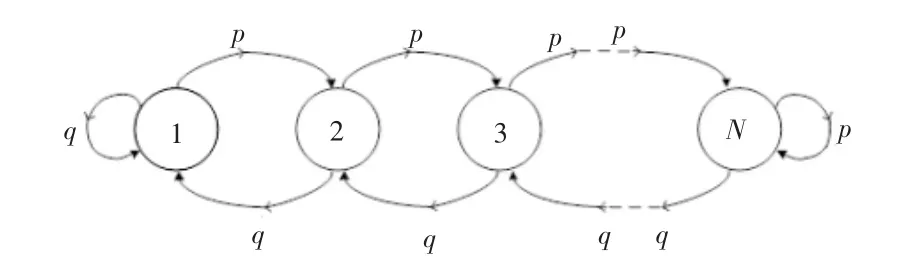
图2 基于Markov 链的电池状态转换图Fig.2 Markov-chain-based battery state transition
该模型仅考虑相邻状态间单位时间内的电能转换,每个数字代表一种荷电状态(SOC):1 表示储能装置处于完全放电状态,N 表示储能装置处于完全充电状态。 此模型表示在负荷为固定值的情况下,仅考虑相邻状态之间的转换,假定L 为常数,随机变量Xr取值只要两个,这并不符合实际。 因此,对此模型进行了拓展,允许在一个有限集合中取值(Xr-L)。
本文所提出的改进Markov 链模型如图3 所示。

图3 改进的Markov 链模型图Fig.3 Improved Markov chain model diagram
该模型在原有模型的基础上考虑了多种可能的状态变化,更符合电池的充放电特性。特别是对电池状态转换进行了建模,在每个时间步中,每个状态中有M 个转换步。 k11和kNN分别表示在下一时间步保持状态1 和N 的概率。 状态之间的转移概率用pi表示,其中i 表示相对于单位功率Δ,即单位时间内在电池中存储或获取的功率。例如:p1是向相邻状态的过渡, 单位时间内存储到蓄电池的功率为Δ;p-1表示向相邻状态的过渡, 单位时间内从蓄电池中获取的功率为Δ。此外,(Xr-L)的状态扩展为

式中:Xt为t 时段的能级;Xt+1为1 s 后的能级;Dt为1 s 内向蓄电池存储或从蓄电池获取的能量,

式中:π 服从正态分布。
极限概率为每个状态结束时的预期概率。 极限概率已知后,失负荷概率(LOLP)即电池处于某荷电状态时,在Markov 链中电池过渡到完全放电状态, 无法满足i 个Δ 单位功率不足的概率。 用πE表示光伏储能系统不能满足负载的概率,可用式(19)确定特定储能容量的LOLP。
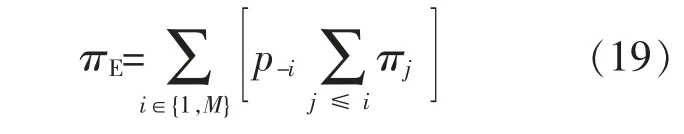
2 储能优化模型
2.1 目标函数
在区域电网的分布式光储系统优化控制中,以区域电网电压波动最小为优化目标, 其目标函数可表示为

2.2 约束条件
在光储联合的区域电网中,系统任意节点、任意时刻的有功、无功满足以下约束方程[14]~[18]:


2.3 基于粒子群的光储协调优化方法
为实现分布式光储的快速协调控制, 本文采用基于竞争机制的粒子群优化控制算法。 通过采用粒子群优化控制快速实现计算结果的收敛,更好地保证算法结果的分布性, 进一步提升粒子群优化的计算速度以及优化位置的更新计算。 所建立的模型为
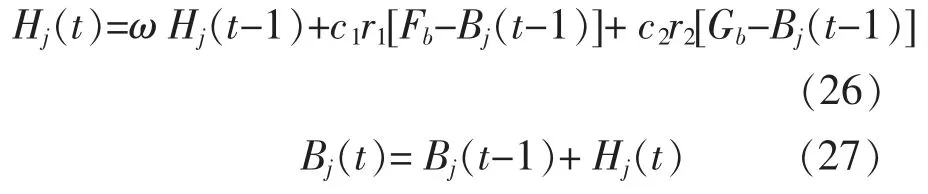
式中:Hj为粒子群优化算法中第j 个粒子的搜索速度;c1为搜索过程中积累的经验;c2为工程计算的经验系数;Fb为粒子群优化计算历史过程中的最佳位置;r1,r2为0~1 的随机常数;Bj为当前计算步时第j 个粒子的位置;ω 为粒子群计算的惯性系数;Gb为计算过程中粒子j 在种群的历史最佳位置。
基于粒子群的储能协调优化运行控制策略如图4 所示。

图4 粒子群储能协调控制框图Fig.4 Block diagram of particle swarm energy storage coordination control
3 仿真验证
图5 为所搭建的区域电网图。

图5 仿真系统图Fig.5 Simulation system diagram
图5 显示了分布式储能及分布式电源数量和位置。采用搭建的系统对所提方法进行仿真分析,系统中各参数列于表1。

表1 系统参数Table 1 System parameters
在分布式光伏出力发生波动时, 为保证系统电压的稳定, 通过优化控制得到不同节点处的分布式储能的投入状态(图6)。 根据负载的变化,4个节点的储能装置在不同时间段内进行调整。
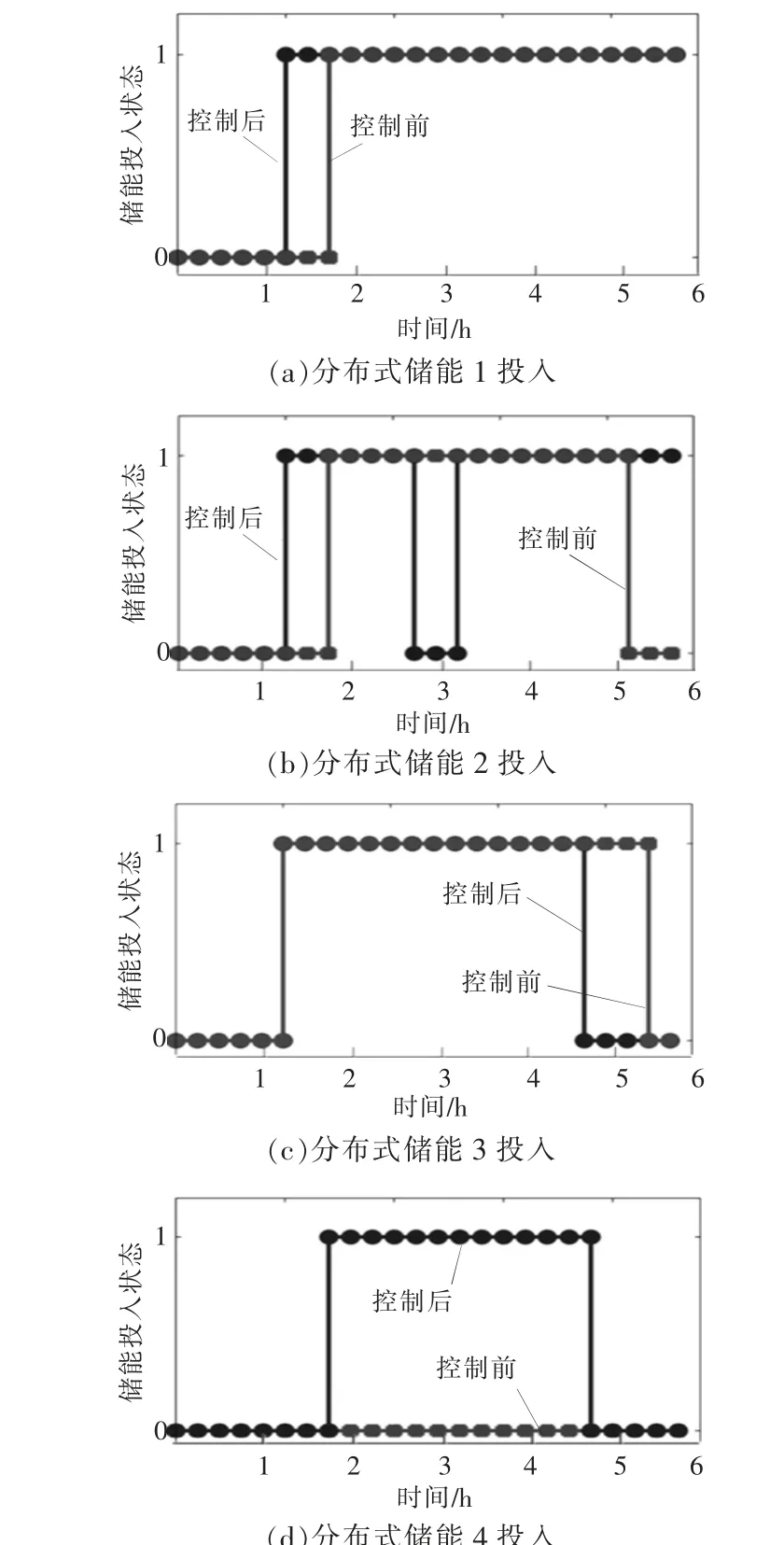
图6 分布式储能投入状态Fig.6 Distributed energy storage investment status
分布式电源出力如图7 所示。 由图7 可知,在第2 分钟时,分布式电源出力突然出现大幅度下降,为保证区域电网供电的可靠性,投入了分布式储能。

图7 分布式电源出力Fig.7 Distributed power output
图8 为优化控制前后,区域电网不同节点母线处的电压波形仿真结果。

图8 不同节点电压波动曲线Fig.8 Voltage fluctuation curve of different nodes
由图7 可以看出, 在可再生能源发生出力波动或者出现故障后,伴随可再生能源出力的降低,母线处的电压幅值跌落。通过优化控制,合理地安排储能装置的充放能时间, 区域电网母线处的电压得到明显改善,区域电网电压稳定性显著提高。仿真结果还显示, 在系统无功出现较大缺额情况下,当电压突然跌落时,系统迅速提升电压,维持电网在额定电压下运行。
4 结论
通过分析区域电网中分布式储能的运行模式及蓄电池的充放能特性, 在所建立的光储协调控制模型的基础上, 有效地实现了分布式储能与光伏出力的协调配合。
在以系统电压波动最小为优化目标的控制算法下,考虑分布式储能的充放电性能约束条件,通过粒子群优化算法计算, 可实现光伏与储能充放能的合理配合。
通过对典型分布式光储联合系统的仿真、分析和验证表明, 投切相应的电池储能可有效缓解系统的电能冲击。 采用本文所提出的方法能够提升区域电网的电压稳定性水平。

