三峡库区紫色砂岩不同发育程度土壤入渗特征及其影响因素
张轩铭,戴翠婷,李朝霞,周怡雯,王天巍,李 豪
(1.华中农业大学水土保持研究中心,武汉 430070;2.武汉蓝天绿野咨询设计有限公司,武汉 430021)
土壤入渗是指降水从地表渗入土壤形成土壤水分的过程,作为水文循环中的重要一环,入渗是降水等地表水转化为土壤水的唯一途径,土壤入渗能力深刻影响着降水的再分配过程,对降水的有效储存与转化利用至关重要。有研究证实土壤入渗主要受土壤性质的影响,而土壤性质与土壤发生发育过程密不可分。
土壤发育是指从岩石的风化产物或堆积物经受成土因素作用开始,经过物质与能量的转化和迁移,并使土体构造发生变化,形成目前状态下土壤的过程。母质在不同环境条件的交互作用下形成不同发育程度的土壤。土壤发育程度的差异不仅导致明显不同的土壤剖面层次结构,土层间性质也具有明显的变异。Torrent等研究认为,成土作用影响土壤的颗粒粒径分布,土壤中砂粒含量与黏粒含量分别随土壤发育程度的增加而减少和增多,而且随成土时间增长,土壤深层的黏粒含量逐渐增加。有研究表明,土壤层次间容重、质地、孔隙度等的差异影响入渗过程,非均质的土壤剖面层次水分运动明显不同于均质土壤,主要表现为非均质土在土壤分层处存在毛管障碍,降低土壤入渗速率。吴奇凡等认为,土壤剖面层次结构上粗细质地土层的排列顺序导致土层间土壤水力参数的不同,进而影响土壤的入渗特征,细质土的分布位置决定整个土体的土壤饱和导水率大小;Schwen等研究发现,剖面土壤水力特性垂向变化明显,随着土层深度的加深,土壤导水率逐渐下降,且导水率的变化与土壤结构密切相关。因此,本研究着眼于不同发育程度土壤的入渗特征以及探究其入渗差异的关键影响因素。
紫色砂岩广泛分布于三峡库区及其周边的丘陵和山地区域,具有疏松易崩解的特征,在亚热带湿润气候条件下碎裂成碎石,进入土壤后在相对较短时间内风化成土。受到母质特性和不同地形下的侵蚀堆积过程的影响,发育程度较低的土壤土层薄、土壤分层不明显,表土层向下即过渡到母质层,发育程度较高的土壤具有明显的层次结构,且土层间土壤性质差异明显。不同的剖面结构使土壤入渗、产汇流、土壤侵蚀等过程受土壤发育程度影响显著,因此研究三峡库区紫色砂岩不同发育程度土壤入渗性质对该区域水分运移规律和土壤侵蚀防治具有重要意义。
1 材料与方法
1.1 研究区概况
本试验研究区位于三峡库区秭归县王家桥小流域(110°40′—110°47′E,31°05′—31°15′N)。王家桥小流域属长江二级支流,流域总面积为16.7 km,海拔最高1 180 m,最低184 m。流域属于北亚热带湿润季风气候,气候温和、四季分明、雨热同期。多年平均降水量为1 192 mm,雨量分布不均,降水集中在4—9月。流域属于典型的山区小流域,地形切割强烈,形成山高坡陡的地貌特征。流域出露中生界侏罗系蓬莱镇组地层,成土母质以紫色砂岩为主。根据前期土壤调查,由土壤系统分类确定研究区内紫色砂岩发育的主要土壤类型包括紫色正常新成土、紫色湿润雏形土和钙质湿润淋溶土。
1.2 样品采集
前期在研究区挖掘土壤剖面并进行土壤调查,选取流域内典型的3种不同发育程度土壤类型,由低到高依次为S1(新成土)、S2(雏形土)、和S3(淋溶土),综合考虑植被覆盖度、地形状况等因素,在保证这些条件基本一致的条件下,每种土壤类型设立林地、果园、耕地3种不同土地利用的样地用来进行原位圆盘入渗试验,再根据各种发育程度最大土壤厚度分层取环刀样品和散土样品来测定土壤性质,S1(新成土)取0—10 cm土壤样品;S2(雏形土)取0—10,10—20,20—30 cm土壤样品;S3(淋溶土)取0—10,10—20,20—30,30—40 cm土壤样品。样地土壤基本信息见表1。

表1 样地基本概况
1.3 试验方法
试验于2020年9—11月进行,使用圆盘入渗仪原位测定样地土壤入渗率。圆盘入渗仪的储水管高100 cm,直径为3.7 cm,入渗底盘直径为12 cm。试验前去除样点表面的枯枝落叶等杂物,整理出足够的平整地面,在环内铺满3 mm厚的细沙并用钢尺刮平,然后将入渗仪充满水,并检查气密性,随后赶出气泡。在土壤入渗试验过程中,前10 min每隔30 s记录1次入渗量,10~40 min每隔5 min记录1次,40~90 min每隔10 min记录1次。计算出初始入渗率、平均入渗率、稳定入渗率、饱和导水率作为入渗指标。其中初始入渗率=最初入渗时段内渗透量/入渗时间,本试验取前3 min的平均入渗率作为初始入渗率;平均入渗率=达到稳渗时的渗透总量/达到稳渗所用时间;稳定入渗速率为单位时间内的渗透量趋于稳定时的渗透速率。采用吸管法测定土壤颗粒组成、环刀法测定土壤容重、总孔隙度、毛管孔隙度等指标,重铬酸钾—外加热法测定土壤有机质含量。
1.4 数据处理与模型选取
采用SPSS 25.0软件进行数据分析,Origin 2020软件进行土壤入渗过程模拟与制图。对入渗过程进行定量描述与模拟的模型迄今还未得到统一和普遍适用,因植被、土壤类型存在差异,不同区域适宜的拟合模型也不尽相同;而合适的土壤入渗模型则是对地区水文过程模拟的重要手段。本文使用3个目前主流的土壤入渗模型用于入渗过程模拟:
(1)Kostiakov模型:
()=-
(1)
式中:()为土壤入渗率(mm/min);为入渗时间(min);、为拟合参数。
(2)Philip模型:
()=05-05+
(2)
式中:、为与入渗有关的经验系数。
(3)Horton模型:
()=+(-)e-
(3)
式中:为初始入渗率(mm/min);为稳定入渗率(mm/min);为试验求得的经验参数。
2 结果与分析
2.1 不同发育程度土壤基本理化性质
不同发育程度土壤理化性质见表2。不同发育程度的土壤土层间理化性质指标均具有一定的差异。土壤容重随土层深度的增加而增加,20—40 cm的2个土层显著大于0—20 cm的2个土层(<0.05);土壤总孔隙度随土层深度的增加而减小,且0—20 cm的2个土层与20—30,30—40 cm土层之间具有显著差异(<0.05);土壤毛管孔隙度随土层深度的增加而逐层减小,但不具有显著差异(>0.05);土壤通气孔隙度随土层深度的增加而逐层减小,30—40 cm土层显著小于0—30 cm的3个土层(<0.05);土壤砂粒含量随土壤发育程度的增加而显著减小,即S3

表2 典型土地利用不同发育程度土壤理化性质
2.2 不同发育程度土壤入渗特征
从图1可以看出,不同发育程度的土壤入渗指标大小均具有一定差异。其中S1、S2、S3初始入渗率平均值分别为5.56,4.94,3.09 mm/min,稳定入渗率分别为1.99,1.81,1.74 mm/min,平均入渗率分别为3.91,3.60,2.57 mm/min,饱和导水率分别为2.23,1.93,1.80 mm/min。林地、耕地、果园均呈现明显的随发育程度增加土壤入渗率减小的趋势,即S1>S2>S3。

图1 不同发育程度土壤入渗特征
土壤入渗速率随时间变化过程见图2。不同发育程度土壤入渗过程有较大差异,但均表现出初始入渗率>平均入渗率>稳定入渗率的趋势,入渗开始初期入渗速率较高,而后随着时间推移逐渐降低,最终稳定于定值,即达到稳定入渗阶段。S1在整个试验过程中的入渗速率整体明显大于S2和S3,而S3的入渗速率则明显小于S1和S2。
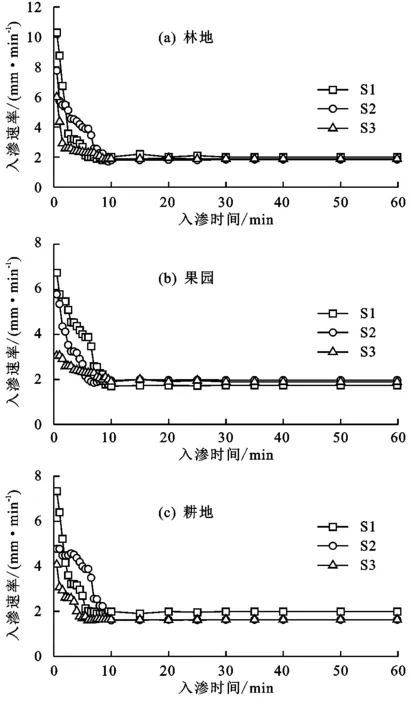
图2 不同发育程度土壤入渗过程
2.3 入渗特征影响因素
土壤入渗状况受到土壤容重、土壤孔隙度、土壤质地、有机质含量、土壤结构等性质的影响。因此,对土壤入渗特征与影响土壤入渗的影响因素进行相关分析。从表3可以看出,初始入渗率与容重、总孔隙度、通气孔隙度、黏粒含量之间呈极显著相关关系,稳定入渗率仅与有机质含量极显著相关(<0.01);平均入渗率与总孔隙度、通气孔隙度、土壤容重、黏粒含量、砂粒含量之间呈极显著相关(<0.01);饱和导水率与总孔隙度、土壤容重之间呈极显著相关,与毛管孔隙度呈显著相关(<0.05)。
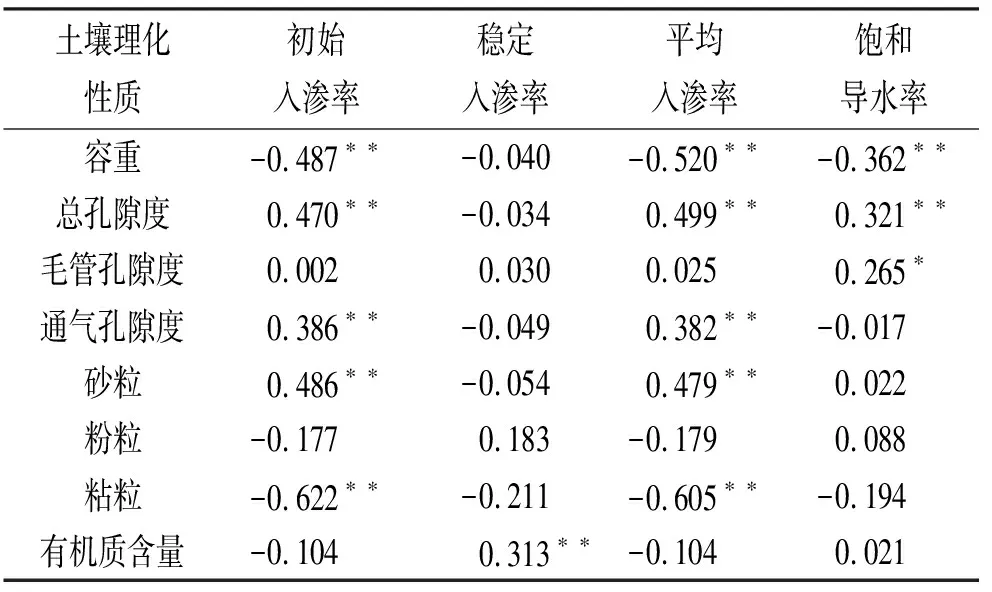
表3 土壤入渗特征与理化性质间的相关关系
采用冗余分析(RDA)研究土壤入渗速率与土壤理化性质之间的关系,将土壤理化性质作为解释变量,土壤入渗速率作为响应变量进行分析,可通过其夹角大小来确定变量间的相关性,夹角越小,相关性越强,当夹角<90°时,解释变量与响应变量呈正相关;当夹角>90°时,解释变量与响应变量呈负相关。可以通过将1个变量与在其他变量的箭头投影来读出其近似相关性。土壤理化性质对土壤入渗特征值在第1排序轴(RDA1)的解释量为48.29%,在第2排序轴(RDA2)的解释量为41.73%,即前2轴对土壤入渗速率的累计解释值为90.03%,累计解释拟合方差值为97.80%,表明前2轴能较好地解释土壤理化性质与土壤入渗速率的关系。其中RDA1可以较好地解释初始入渗率、稳定入渗率的变化,其主要影响因素包括总孔隙度、砂粒含量、黏粒含量、容重和通气孔隙度;RDA2可以较好地解释稳定入渗率、饱和导水率的变化,其主要影响因素包括毛管孔隙度、粉粒含量、有机质含量、容重和通气孔隙度(图3)。
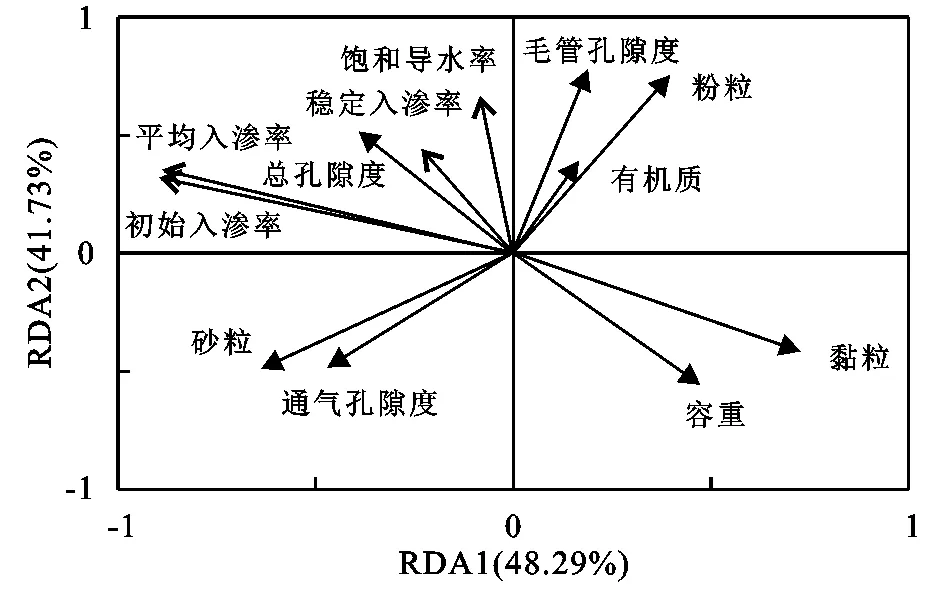
注:实心箭头为解释变量;空心箭头为响应变量。
2.4 入渗模型拟合效果
为进一步探究经典入渗模型对不同发育程度土壤入渗的适用性,使用3种经典入渗模型对入渗过程进行拟合,拟合结果见表4。Kostiakov入渗模型中,为经验入渗常数,即第1个单位时段内的平均入渗速率,可用来表征初始入渗率的大小;值的大小可以表明入渗速率随时间减小的速度,值越大,则入渗速率随时间减小的速度越快。由表4可知,Kostiakov方程拟合的参数值从小到大依次为S3 表4 不同发育程度土壤入渗过程模拟结果 对入渗过程的拟合效果可以用回归方程的决定系数()表示,其值越大,拟合效果越好。Kostiakov模型、Philip模型、Horton模型对土壤入渗过程拟合决定系数均值分别为0.858,0.832,0.942,说明3种模型均能较好地拟合入渗过程,且Horton模型(为0.830~0.986)对各入渗过程的拟合效果均为最优。而Kostiakov(为0.619~0.950)模型和Philip(为0.486~0.962)模型拟合效果次之,二者相比,Philip模型对S1发育程度的土壤入渗效果优于Kostiakov模型,而对S2和S3土壤入渗过程模拟效果各有优劣。 3种发育程度土壤入渗率均呈现随土壤发育程度增加而减小的趋势。S2、S3初始入渗率较S1分别减小11.47%,41.60%,平均入渗率分别减小12.42%,9.08%,稳定入渗率分别减小3.48%,32.88%,饱和导水率分别减小10.63%,16.95%。同样有研究发现,发育程度最高的土壤具有最低的饱和导水率,这可能由于产生分层的土壤相比均质土壤明显降低下渗速率。在本研究中,S1因不具有明显的土壤分层可被视为均质土体,而S3具有明显的土壤层次,且20—40 cm的2个土层与0—20 cm的2个土层间容重、总孔隙度、通气孔隙度、砂粒含量、黏粒含量均具有显著差异,故对入渗过程形成阻滞效应。由表3和图2可知,土壤入渗率与黏粒含量呈极显著负相关关系,与砂粒含量呈极显著正相关关系,与已有研究结果相似。Zaibon等研究认为,黏粒含量随着土层深度的增加而增加,而黏粒含量高的土层土壤质地较细,通常具有较少的大孔隙,因此土壤深层入渗速率迅速下降。S3的土壤入渗率明显低于S1和S2,可能是由于较高发育程度的土壤通过增加深层细颗粒占比而导致土壤入渗速率降低。由相关分析可知,土壤入渗率和土壤容重呈极显著负相关关系,与总孔隙度和通气孔隙度呈极显著正相关关系。土壤容重是土壤紧实度与孔隙度的间接反映,土壤入渗是水分在土体孔隙内流动并且不断深入的过程,所以容重和孔隙度对土壤入渗产生较大的影响。已有研究表明,低发育程度的土壤具有较高的孔隙度和较低的容重。综上所述,本研究中发育程度较低的土壤可视为近似均质土,且颗粒较粗,孔隙较大,导致容重偏小,土壤入渗速率和饱和导水率较大;而发育程度较高的土壤具有明显的土壤分层,且深层土壤颗粒较细,容重偏大,孔隙较小,不利于土壤水分下渗。 Kostiakov模型、Philip模型、Horton模型均能拟合不同发育程度土壤入渗过程,其中Horton模型拟合效果最优,其次为Kostiakov模型,而Philip模型拟合效果不够理想。Horton模型虽是纯经验公式,但能描述长时间的入渗特征,且模型参数具有物理意义,是模拟本研究入渗过程的最优模型;Kostiakov模型假设初始入渗速率无限大,当时间无限延长时,入渗速率趋近于0,本试验中在达到稳定入渗后入渗率趋于定值,因此拟合效果不够理想;Philip模型是在半无限均质土壤有积水条件下求得,只适用于均质土壤一维垂直入渗的情况,仅对近似均质土的S1拟合效果较好,且在原位自然土壤下三维入渗应用有一定局限性。相比较而言,Horton模型对紫色砂岩不同发育程度土壤入渗过程拟合效果最优,适用性最强。 (1)不同发育程度土壤入渗速率随发育程度的增高而减小,初始入渗率、平均入渗率、稳定入渗率、饱和导水率均表现为S1(新成土)>S2(雏形土)>S3(淋溶土)。 (2)不同发育程度土壤因土壤性质差异对土壤入渗具有显著影响,初始入渗率、平均入渗率、稳定入渗率、饱和导水率与总孔隙度、毛管孔隙度、通气孔隙度、砂粒含量呈正相关关系,与容重、黏粒含量、有机质含量呈负相关关系。 (3)Kostiakov模型、Philip模型、Horton模型均能拟合不同发育程度土壤入渗过程,决定系数由大到小依次为Horton模型>Kostiakov模型>Philip模型。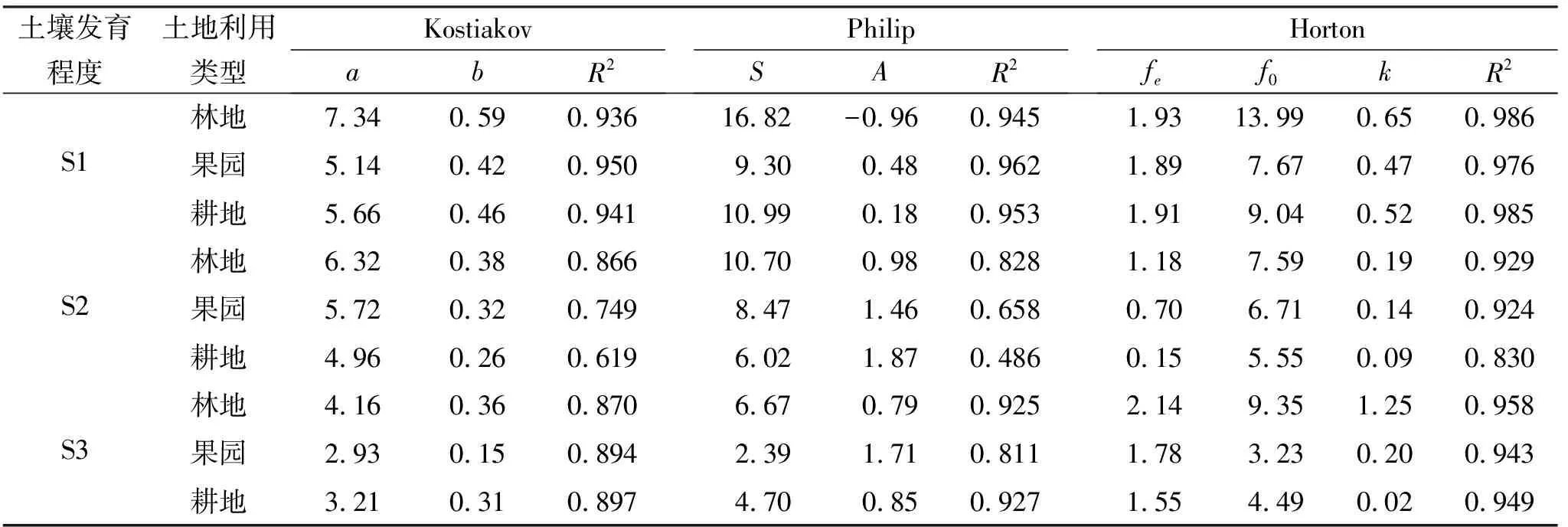
3 讨 论
4 结 论

