基于特征提取极限学习的卧姿压力图像识别

袁先启，蒋永翔，夏红超

（天津职业技术师范大学机器人及智能装备研究院，天津 300222）

人的一生中有1/3 时间在睡眠中度过，睡眠质量直接影响人的身体健康。卧姿作为评判睡眠质量和预防突发疾病的指标之一，其识别一直都是学者研究的热门课题。日常的卧姿主要包括仰卧、俯卧、左侧卧和右侧卧4 种。Baranowski 等[1]提出卧姿对睡眠呼吸障碍有着重要的影响。这4 种卧姿的识别不仅可以辅助诊断心血管病、肥胖症、糖尿病等疾病[2]，还可为评价睡眠质量和诊断睡眠呼吸障碍提供依据[3]。目前，人体姿态识别研究方法主要分为4 种：①肌信号提取肌电信号[4]和肌音信号[5]的方法[A1]。采用支持向量机对肌信号中的时域、频域等特征进行分析，识别人体姿态特征，由于这种识别方法无法实现精细动作的识别，因此分类精度有待提高。②计算机视觉采集的方法，包括3D 相机[6]和视频记录等[A2]。利用3D 相机对人体动作进行记录，再利用隐马尔科夫模型（HMM）[7]对人体动作等进行建模和识别，这种方法只有在训练集较少的情况下才能展示出很好的效果，对大规模的数据集训练易出现过度拟合。③可穿戴传感器采集法。主要包括加速度计和陀螺仪传感器等[8-9]，通过传感器采集人体信号，提取相应的特征值，运用随机深林法、支持向量机算法、K-最近邻的方法进行特征识别[10]，最终实现人体姿态识别，这种具有侵入性穿戴式的传感器极易给人们造成不舒适。④压力传感器图像采集法。利用压力传感器进行人体压力图像的采集，通过图像分析对人体卧姿进行识别。耿读艳等[11]通过压电薄膜传感器采集心冲击（BCG）信号，并进行局部特征提取，利用支持向量机实现卧姿识别。该方法由于BCG 波形受到个体差异和环境的影响，支持向量机算法出现了极大的误差。根据以上方法，本文提出利用压力传感器采集人体背部压力图像的方法，通过极限学习算法识别卧姿，实现疾病的诊断。

1 极限学习模式（ELM）算法

ELM 是以神经网络为单隐藏分层学习方法的重要工具，在ELM 中输入层的权重随机分配计算[12]，极限学习算法的结构模型如图1 所示。

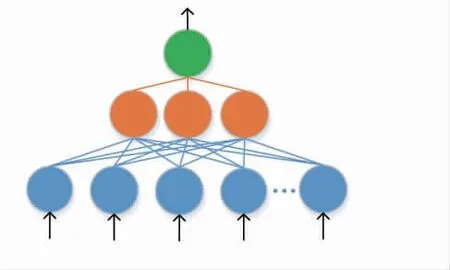
图1 极限学习算法的结构模型

本研究ELM 借助神经网络，具有较快的学习能力。ELM 选择隐藏权重神经元，与一些经典算法相比，模型结构选择的总体计算时间及实际训练时间较短[13]。ELM 具有很高的性能且对分类精度隐藏层起始参数（链接权重、偏移值、节点等）影响很大[14]。

结合图1 极限学习模型，人工神经网络的输出ELM数学模型可描述为

式中：n 为训练样本；x1…n为输入向量；y1…n为输出向量；β1…m为输出层权重；w1…n，1…m为输入层和输入层之间的权重隐藏层；b1…m为阈值函数；输出函数g（*）为激活功能。

对于给定的输入输出样本，利用隐藏层输出矩阵H 和隐藏层输出层权重b，ELM 计算输出

H 为ELM 隐藏层的输出矩阵，H 的第i 列是第i个隐藏节点的输出。在ELM 中，可以根据训练集隐藏层输入层权重和隐藏层输出层权重的随机参数（wi，bi）得到H。ELM 的输出重量β 计算式为

式中：H*为矩阵H 的广义逆矩阵。

n 个训练样本，x1，x2，…，xi为训练集，i ＝1，…，n，隐层输出函数g（*），隐藏节点的数目n 作为输入。ELM算法步骤：①随机分配输入权重w 和输出权重B，w=[w1，w2，…，wn]，B = [b1，b2，…，bn]；②计算隐层输出矩阵H；③计算输出重量β，β=H*×y。

2 人体压力特征提取实验

2.1 实验要求及设备安装

选取80 名健康实验者（男性和女性各40 名）参与实验。实验者年龄为20～27 岁，身高为160～180 cm，体重为45～80 kg。所有实验者参与实验过程中需穿着单薄上衣，以免衣物过厚对采集的压力信息造成干扰。

本次实验使用日本东海橡胶公司生产的SR 智能压力传感气垫，简称SR 传感器。SR 传感器由16×16 个压力传感器阵列组成，测量面积为450 mm×450 mm。SR压力传感器阵列是电极与布线共同印刷成型的，使用USB 与采集系统接口相连，实验者躺在测定区域测定背部的压力分布。测定结果在上位机上显示分布压力图像和压力数值。压力传感器的安装方式如图2 所示。

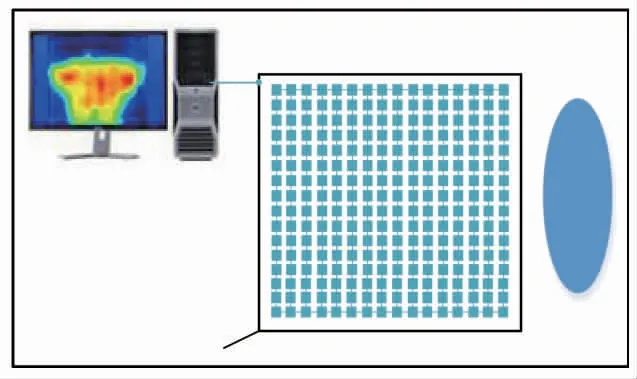
图2 压力传感器安装示意图

2.2 数据采集

为了训练更多特征参数，提高极限学习算法的稳定性，需要采集每位实验者的4 种卧姿，一种卧姿需要重复采集4 张压力图片，80 位实验者共采集1 280张图片。为避免实验者对实验环境与卧姿不适应而造成的干扰，要求实验者每次躺下平静30 s 后再开始采集信息，信息采集数据传输至上位机并显示，记录压力分布。

3 极限学习卧姿的识别

3.1 典型卧姿选择及卧姿图像采集

选择4 种卧姿作为本次研究的主要模型，如图3所示。这4 种卧姿是人们在卧床过程中的常见姿势，也是影响睡眠舒适度的重要姿态[15]。卧姿作为评估人体睡眠质量的关键因变量，是睡眠质量评价的主要方法[16]。以实验者1 为例，用50×50 的压力传感器阵列采集了4 种卧姿的背部压力图。

图3 4 种卧姿

3.2 压力图像特征提取和处理

首先采用Matlab 软件将采集到的背部压力图像进行灰度二值化处理、边缘算子提取等操作，最终得到周长、面积等几何特征。几何特征提取流程如图4 所示。

图4 几何特征提取流程

对压力图像进行中值滤波降噪、灰度处理，将灰度图像转换成二值图像，再用Canny 算子对二值图像进行边缘轮廓的提取，Canny 算子的阈值为200，得到边缘轮廓图像，通过提取边缘轮廓，可以清晰地看出压力图像的外部边缘轮廓，根据图像的最外层边缘，提取最小包围矩形，提取后的最小包围矩如图5所示。

图5 最小包围矩

3.3 特征参数选取和计算

从压力分布图像中提取3 类16 个特征参数：最小包围矩形计算的几何特征参数包括周长、面积、Hu1-Hu7；提取40 名男性实验者的压力分布最小包围矩，求取最小包围矩的周长和面积平均值，去掉周长和面积平均值的最大和最小值，从剩余的数据中更能体现出卧姿数据的真实性，包围矩形周长分布曲线和面积分布曲线分别如图6 和图7 所示。

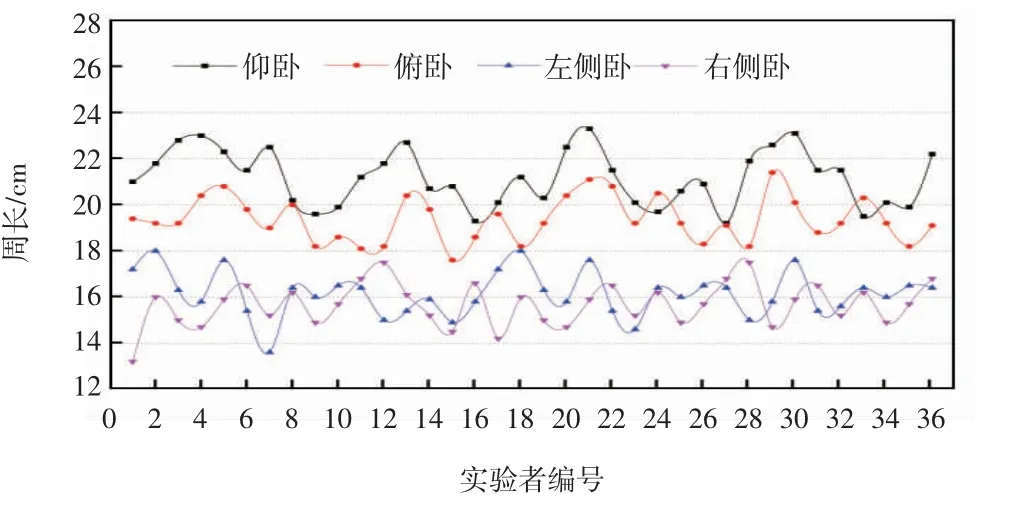
图6 包围矩形周长分布曲线

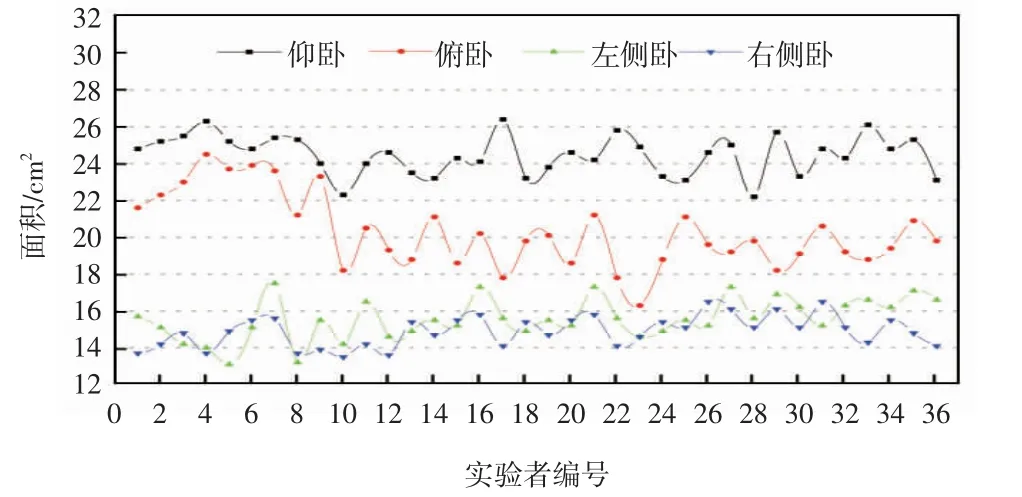
图7 包围矩形面积分布曲线

从图6 和图7 可以看出，在包围矩的周长和面积分布曲线中，同一人的仰卧和俯卧包围矩的周长和面积均大于侧卧的周长和面积。

Hu 矩是利用二阶和三阶中心距提取图像的位置、大小等特征构造出7 个不变矩，其具有识别稳定，缩放、平移、旋转不变等优点[17]。Hu 矩图如图8 所示。

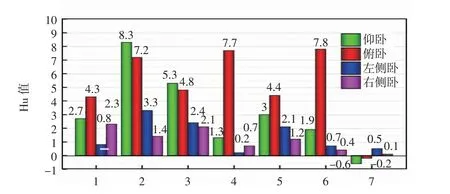
图8 Hu 矩图

从Hu 矩的几何特征参数可以看出，仰卧俯卧的Hu1-Hu6 均大于侧卧的Hu1-Hu6，仰卧俯卧的Hu7均为负，侧卧的Hu7 均为正。俯卧的Hu 矩值相对较高，虽然仰卧俯卧的Hu 值与侧卧的区分比较明显，但是仰卧和俯卧的Hu 值区分比较模糊，左侧卧和右侧卧同样难以区分。

本实验采集80 人的压力分布图和压力值，用采集的压力值计算压力平均值、压力标准差，再用采集的压力分布图计算图片信息熵平均值、熵标准差，最后把压力平均值、压力标准差、压力图熵平均值和熵标准差分别取均值，压力信息能量特征图如图9所示。

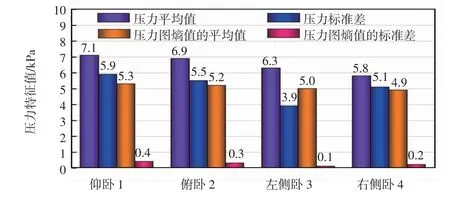
图9 压力信息能量特征图

根据压力信息能量特征图的显示，做出如下分析。

（1）仰卧、俯卧状态下的压力平均值和压力标准差均大于侧卧的平均值和标准差，仰卧的压力平均值和压力标准差最大，左侧卧的压力平均值和压力标准差最小。

（2）仰卧、俯卧的压力图熵平均值和压力图熵标准差均大于侧卧图熵平均值和图熵标准差。

（3）仰卧、俯卧的压力图熵平均值和左侧卧、右侧卧的压力图熵标准差均难以区分。

由于传感器测量得到不同卧姿压力云图，通过提取压力图中RGB 颜色均值进行特征分析，RGB 均值如表1 所示。

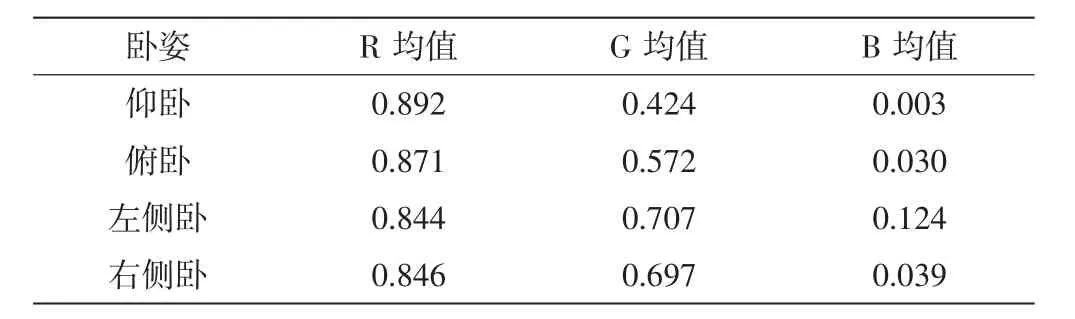
表1 颜色特征值的提取

通过RGB 颜色特征值的提取可知，仰卧俯卧状态下的R 均值大于侧卧的均值，由于均值相差不大，并不能有效地对卧姿进行评判，因此需要对数据进行整合分析。获得16 个特征参数后，采用式（6）对数据进行归一化处理

式中：Qi为上述16 个特征参数；Qi*为归一化特征值。

通过对数据归一化融合处理，引入极限学习算法对卧姿进行识别。其中，验证极限学习算法对卧姿识别的有效性和数据归一化处理均是在Matlab 软件中实现。

4 基于极限学习的卧姿识别精度评估

为了评估ELM 的准确性，选择训练样本大小和隐藏节点对4 种卧姿进行监测。选取了80 名实验者，对4 种卧姿每人各选取4 组数据，共获得1 280 组数据。通过上文特征参数的提取与分析，对16 个参数特征进行训练，以sig 为激活函数，随机抽取80、160、240、320 个样本测试集。同时，将隐藏节点数从10 个增加到100 个，每10 个节点增加1 个。不同样本大小和隐藏节点的ELM结果如图10所示。

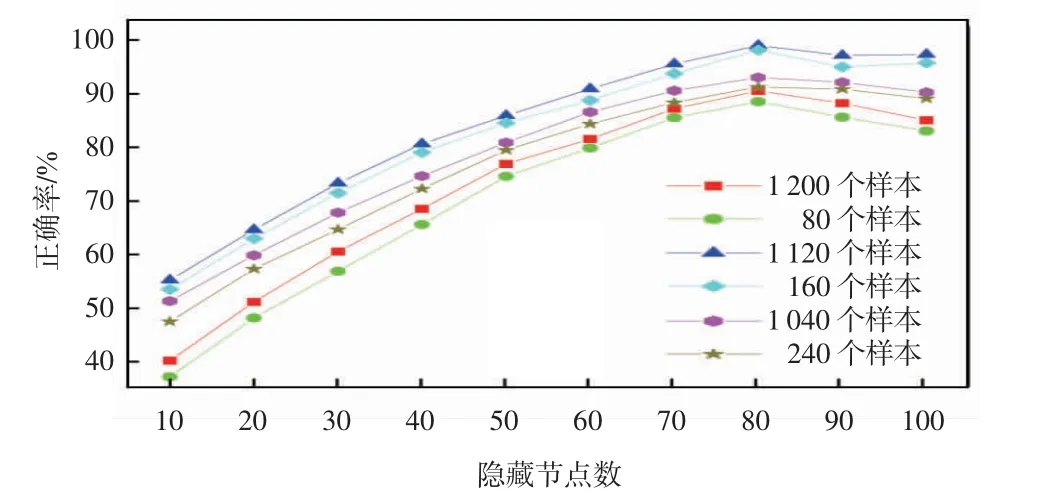
图10 不同样本大小和隐藏节点的ELM 结果

随着隐藏节点从10 增加到80 时，训练集正确率迅速增加。当隐藏节点在80～100 范围内时，训练集虽显示出相当高的精度，但是正确率均呈下降趋势。由不同样本测试集可知，样本训练数量从960 个增加到1 120 个时，其训练集正确率迅速增加。样本训练数量从1 120 个增加到1 200 个时，正确率开始下降。在固定的1 120 个样本训练集中隐藏节点大小为80 更为合理，因为该选择同时考虑了计算的精度和速度。

在选取隐藏节点为80 的情况下，分别选取4 种卧姿的40 组特征数据作为卧姿识别的测试集，160 个测试样本预测图如图11 所示。

这4 种卧姿在模拟训练时已标注，1 为仰卧，2 为俯卧，3 为左侧卧，4 为右侧卧。利用3 类特征值16 个特征参数建立预测模型。模拟结果显示，4 种卧姿识别精度达到了98.75%。因此，通过极限学习算法识别卧姿的方法满足了分类精度要求。

5 结 语

卧姿识别是评判不同疾病群体卧床时采用不当卧姿带来身体压迫导致疾病发生的重要依据。本文通过选用SR 柔性压力气垫对不同卧姿的实验者进行了背部压力图像采集，对采集到的压力图像进行灰度二值化、最小包围矩形的处理，处理后提取灰度图像的几何特征参数（周长和面积），提取压力值和压力图的能量特征参数、颜色特征参数。采用极限学习算法对16 种特征参数进行训练，识别了4 种常见卧姿，卧姿识别的正确率达到98.75%。相比传统单一的提取特征值识别卧姿，该方法综合考虑了全局和局部特征参数的提取，有效地提高了卧姿识别的精度，为无束缚睡眠监测和疾病的预防提供了依据。