《皇极历》外行星算法及精度分析
辛佳岱 唐 泉
(西北大学科学史高等研究院,西安 710127)
自西汉《太初历》起,行星理论就是历法的重要内容。隋代之前的历法家根据行星和太阳的平运动来推算行星的见、伏等特征天象发生的时刻及其位置。公元560年前后,张子信发现太阳与行星运动不均匀现象之后,历法家不断探索行星不均匀运动修正算法,以达到提高行星位置计算精度的目的。刘焯的《皇极历》(600)是现存中国第一部设计算法修正太阳与行星不均匀运动的历法,并且影响了隋代及初唐历法中步五星术算法的编制,如张胄玄《大业历》(607)、傅仁均《戊寅元历》(619)和李淳风《麟德历》(665)等三部历法都沿袭了《皇极历》中五星入气加减差算法,以修正行星不均匀运动。僧一行在《大衍历》(724)中,将《皇极历》等历法中的五星入气加减差发展为五星爻象历,基本奠定了中国古代行星不均匀运动修正算法的框架,这个算法在楚衍和宋行古等人编制的《崇天历》(1023)中逐渐趋于成熟,此后一直到元代《授时历》和明代《大统历》,几乎未发生实质性变化。
现有研究涉及行星运动的理论模型[1,2]、隋代及初唐历法中的“五星入气加减差”算法及其精度[3—6]、行星理论中一些重要算法和天文数表[7—10],以及中印行星理论比较研究[11,12]等方面内容。关于行星计算精度的研究主要集中于宋元历法[13—17],对明代《大统历》和《回回历法》也有相关考察[18],而对宋代之前诸历的行星精度较少涉及[19,20]。这对我们全面评价中国古代行星计算精度造成了很大困难。
在中国古代行星理论发展史上,隋代刘焯所制《皇极历》占据着重要地位,故本文以《皇极历》行星算法为研究对象,在对算法术文全面解读的基础上,利用Python语言模拟其算法并讨论行星视位置计算精度,试图回答如下问题:张子信发现太阳视运动与行星公转不均匀现象后,《皇极历》是如何将这些天文发现融入行星运动理论中的?《皇极历》推算行星视位置的误差如何?
1 《皇极历》五星推步思路
《皇极历》记载了五星的天文常数、入气加减差、动态描述和五个推步算法([21],页1963—1970),其行星理论的核心目标是推算行星自始见至始伏期间每日的黄道宿度。隋代历法中通常不考虑行星伏行段的运行情况,这是因为伏行段的行星位置不易观测,无法准确给出其运动状态,当时历法中有“伏不书度”或“伏不注度”等记载([21],页1847、1919)。此外,隋代历法家对内行星运动规律掌握还不够好,如《皇极历》中水星的“入气加减差”仅给出一些经验观测的描述性言语概述,没有量化数据,无法计算任意时刻内行星的位置[3]。故本文的讨论仅限于外行星,不涉及内行星。
外行星包含五个天文常数。以土星为例,依次是土数、伏半平、复日及余、残日及余和见去日。土数(H)意为土星的会合周期,单位为“分”;以“气日法”(A=46644)除之得复日及余(h),即将其换算为以日为单位的会合周期;伏半平(F)意为土星伏行时间的一半,单位为“分”;残日及余是土星会合周期与回归年日数之差。见去日则是晨始见时刻土星与太阳的角距(1)《皇极历》记载木星见去日为14度,火星为16度,土星为16.5度。。
五个推步算法即“推星平见术”“求常见日”“求定见日”“求星见所在度”和“求次日”。其中,求常见日涉及修正行星不均匀运动的五星“入气加减差”;求次日需要借助行星自晨始见至夕始伏的动态描述(五星动态表)。这五个算法是为了计算行星特征天象发生时刻和任意时刻的行星位置而设计。具体而言,前三个算法推算行星晨始见发生的时刻,后两个算法推算在一个会合周期内行星自始见至始伏的每日位置。下面对各个算法的名称、目的及其算法思路进行释读。
(1)推星平见术。按照太阳和行星的平运动推算行星平见时刻与其前一个冬至时刻之间的时距。
据术文,假设Nn为上元时刻距某一年的积年数,t为回归年的日数,h为行星会合周期的日数,f为行星伏行一半的日数,则以会合周期推算行星平见时刻与其前一个冬至时刻的时距γ0,由下式得到:
tNn-f≡h-γ0(modh)
(1)
《皇极历》定义上元O点起于五星与太阳同度的合时刻,而该算法计算平见时刻距离其前一个冬至时刻的时距γ0。因此,从上元至所求年冬至时刻的积日数及余tNn中,减去行星伏行时间一半的日数f,余为A0P,即将起算点从上元行星的合时刻O点推后到上元之后的行星始见时刻A0点。再从A0P中减去整数倍的行星会合周期日数h,不足部分为AnP,以行星会合周期AnAn+1减之,所得为PAn+1,即术文所求γ0。如图1所示。

图1 《皇极历》行星平见时刻与所求年天正冬至时刻的时距
(2)求常见日。考虑行星中心差,对平见时刻进行修正,得到修正后的行星常见时刻距离其前一个冬至时刻的时距。
如图2,根据公式(1)推算出行星平见时刻与其前一个冬至时刻的时距γ0,该算法求经行星中心差修正后的行星常见时刻距离其前一个冬至时刻的时距γ1,由下式得到:
(2)

图2 《皇极历》行星常见时刻与所求年天正冬至时刻的时距
平见时刻与常见时刻之间的修正值Δm,其数值及符号取决于行星平见时刻所入节气。换言之,由于修正行星中心差的结果取决于“平见”所值节气,故称为“入气加减差”算法。
在隋代及初唐的一些历法中,“入气加减差”是为了修正行星中心差对五星始见时刻的影响而设计的算法。虽然五星“入气加减差”算法带有一定的经验色彩,但对于外行星运动不均匀性的改正是有效的、科学的[3]。《皇极历》木星和土星的“入气加减差”算法前人已解释清楚[3—6],火星的“入气加减差”术文记载如下:
平见,在雨水前,以十九乘去大寒日;清明前,又十八乘去雨水日,增雨水所乘者;夏至后,以十六乘去处暑日;小满后,又十五日;寒露前,以十八乘去白露日;小雪前,又十七乘去寒露所乘者(2)严敦杰承担校勘《隋书·律历志》工作时,在《皇极历》术文后的“校勘记”[二三]指出:“又十七乘去寒露所乘者 当作[又十七乘去寒露日,增寒露所乘者]。”参见参考文献[21],第1973页。;大雪后,二十九乘去大寒日,为减,小雪至大雪减二十五日。([21],页1964)
经分析,这段文字应该存有脱讹,陈美东也指出这一点(3)陈美东的校勘是:“……清明前,又十八乘去雨水日,增雨水所乘者;[清明至夏至加二十七日;]夏至后,以十六乘去处暑日;(小满)[处暑]后,又(十五日)[二十八乘去白露日。减处暑所乘者];寒露前,……”参见参考文献[3]。,然而笔者按照校勘改动最少原则,对术文校勘如下:
平见,在雨水前,以十九乘去大寒日;清明前,又十八乘去雨水日,增雨水所乘者;[清明至小满加二十七日;]夏至后,以十六乘去处暑日;小满后,又十五[乘去夏至]日;寒露前,以十八乘去白露日;小雪前,又十七乘去寒露日,增寒露所乘者;大雪后,二十九乘去大寒日,为减,小雪至大雪减二十五日。
上述文字表明,若依据火星会合周期推算的始见时刻“平见”所入节气不同,则火星运动不均匀性影响的改正值就会改变。火星随着“平见”所入节气而引起时间提前或是滞后的改正曲线,如图3所示。

图3 《皇极历》火星“平见日”至“常见日”的改正值曲线
图3中横坐标为黄经值,春分对应黄经0°,每经过一气黄经值的改变量为15°,据此可换算到其余对应的节气。纵坐标为时间改正值,以“日”为单位,正值表示经修正行星不均匀运动得到的“常见日”较“平见日”滞后(如图2中的B″点),负值则表示提前(如图2中的B′点)。
(3)求定见日。考虑太阳中心差,对常见时刻进行修正,得到修正后的行星定见时刻距离其前一个冬至时刻的时距。
与“求常见日”类似,此处要对γ1进行太阳中心差修正,求修正后的行星定见时刻距离其前一个冬至时刻的时距γ2,由下式得到:
(3)
常见时刻与定见时刻之间的修正值为太阳中心差Cs,该算法在《皇极历》步日躔术中记载([21],页1937—1939)。其中,“先后数”即太阳中心差,以“先后数”除以“转法”(52)得到真太阳与平太阳的行度之差。日躔表中罗列二十四气各气初始时刻的太阳先后数,刘焯设计了等间距二次内插算法以求每日先后数([22],页152—155)。
(4)求星见所在度。由于外行星运行速度较太阳慢,故以定见时刻太阳的位置减去“见去日”,即可得到定见时刻行星的位置。
术文中记载定见时刻太阳位置的方法是:计算行星定见时刻所在晨前夜半的太阳位置,再加上定见日余对应的太阳行度即可([21],页1969—1970)。为了便于利用Python语言模拟其算法,此处以一种等价方法替换。根据《皇极历》步月离中的“推日度术”([21],页1950—1951),计算所求年冬至时刻的太阳位置,再由公式(3)得到行星定见时刻距离所求年冬至时刻的时距γ2以步日躔中的太阳中心差算法推算出在γ2内太阳运行的度数,即可得到定见时刻的太阳位置。
以土星定见时刻的位置为例,若令λ0为太阳在所求年冬至时刻的黄道宿度,d为在γ2内太阳的实际运行度数,并且根据土星“见去日”常数得知定见时刻土星落后太阳16.5度。故土星定见时刻的黄道宿度λ土,由下式得到:
λ土=λ0+d-16.5
(4)
(5)求次日。计算行星在任意一日的位置。由公式(4)推算出行星定见时刻的位置,在此基础上累加行星各日行度,即可得到行星定见之后至始伏期间每一日的位置。
《皇极历》记载了行星在一个会合周期中自始见至始伏的逐日行度。根据土星的动态描述([21],页1966),罗列出土星自晨始见至夕始伏的运动状态,如表1所示。

表1 土星动态表
由表1可见,土星运动状态划分为五个段目:前顺行、前留、逆行、后留和后顺行(4)前顺行段目以土星晨始见为起点,后顺行段目以土星夕始伏为结束。《皇极历》术文中并未出现“前顺行、前留”等这些名称,是我们为了方便描述,依据唐代历法五星动态表中的名称,结合《皇极历》土星动态描述给出相应段目的名称。,并未给出伏行段目行星的动态描述,仅以“伏半平”和“见去日”两常数笼统刻画行星伏行的时间和度数。木星的运行状态与土星类似,相对容易理解。
《皇极历》中火星的运动划分为七个段目:前疾、前迟、前留、逆行、后留、后迟和后疾。火星在前疾与后疾段目的动态描述与以往历法大有不同,表现为这两段目的火星运动状态并非直接给出,而是要先判断火星前疾和后疾初日距离其前一个冬至的日数,以此推算火星在该段目上的运行时间(日率)和度数(度率)等([21],页1964—1965)。这种处理方式与印度6世纪中叶《五大历书汇编》(Pacasiddhāntikā)中的《宝莉莎历数书》(Paulia)将火星动态表与行星的黄经相联系的设计方案非常类似[23]。
火星在前疾与后疾两段目动态描述首先根据火星晨始见时刻或后疾初始时刻所值节气,对应算出火星在前疾段或后疾段的日率和度率,之后在某些节气上,还要对日率和度率进行二次修正。其中,对某些节气的日率、度率二次修正时,有“半度之行”的说法,如术文言“白露至寒露,初日行半度,四十日行二十度”([21],页1964)。以往学者的理解是火星晨见初日运动速度均为半度(5)张培瑜等学者认为白露至寒露时,火星晨见初日运动速度均为半度,见参考文献[24]。刘洪涛认为火星在白露至寒露间初见的平均速度是日行半度,见后匀速行40日移20度,见参考文献[25]。王应伟认为术文疑有脱字或脱句,见参考文献[26]。。唐泉依据初唐《戊寅元历》《麟德历》中对火星前疾段目的修正法则时的论述,认为此处“半度之行”,并非火星晨始见在白露至寒露这个时段内,其初日视行速为0.5度/日,而是若在这个时段内要对原有日率和度率进行二次修正,即日率减去40日,度率减去20度[19]。
中国传统历法家计算行星位置的基本思路在《皇极历》中已雏形初现。概言之,其五星推步的思路是:首先,依据行星会合周期推算平见日;其次,以行星中心差修正平见日,得到常见日,再以太阳中心差对常见日加以修正,得到定见日;再次,推算定见时刻的行星位置;最后,在此基础上再累加五星动态表中的每日行度,得到行星的每日位置。
2 《皇极历》行星算法的计算机模拟与算例
为了加深对《皇极历》五星推步算法的理解,此处以公元600年冬至之后的土星在一个会合周期内自晨始见至夕始伏每日夜半的极黄经推算过程为例,给出计算实例。
《皇极历》中与土星位置相关的基本天文常数包含:上元距开皇二十年(600)积年数为N600=1008837年(6)此处的积年数包含所求年,历法中通常称为“算上”。。岁数T=17036466.5,土数H=17635594,伏半平F=864995,它们均以气日法A=46644为分母,由此得到:
(5)
参照上一节《皇极历》计算行星位置的基本思路,为了得到土星每日夜半的历取黄经值,根据五星推步算法过程将其分为五个步骤执行。具体如下:
第1步:求公元600年冬至时刻距离后一个土星平见时刻的时距γ0。
依据“推星平见术”,将上元积年N600、回归年t、土星会合周期h等常数代入公式(1),即
由此得到γ0约是338.2460日。
第2步:求公元600年冬至时刻距离后一个土星常见时刻的时距γ1。
依据“求常见日”,可知平见与常见时刻之间的修正值取决于行星平见时刻所入节气。《皇极历》平气日数约为15.2185日,由第1步所得γ0推算土星平见时刻入于冬至后的第22气,即入于小雪后约第3.4385日。按照土星入气加减差修正并代入公式(2),即
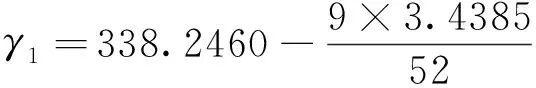
由此得到γ1约是337.6508日。
第3步:求公元600年冬至时刻距离后一个土星定见时刻的时距γ2,以及定见日期。
依据“求定见日”,可知常见与定见时刻之间的修正值取决于行星常见时刻所入节气。土星常见时刻入冬至后第22气约第6.7417日,根据步日躔术,计算出由于太阳运动不均匀性而修正土星常见时刻的数值约是0.7765日。因此,结合公式(3),即
γ2=337.6508+0.7765(日)。
由此得到γ2约是338.4274日。
推算土星定见日期,需要得知公元600年历取冬至时刻的日期。依据“推气术”算法([21],页1936—1937),以如下公式求得历取冬至时刻:
tN600≡r(mod 60)
(6)
代入常数,得到冬至大小余r:
《皇极历》的上元起于甲子日,由上式得到冬至大余为29,可知公元600年历取冬至日的日名为“癸巳”。这一年理论冬至时刻是600年12月18日21时36分,日名也是“癸巳”[27],将“21时36分”化为以日为单位是0.9日。由日名可知恰与历取冬至在同一日,这一日的儒略日序号是1940560。上式算得历取冬至不足一日的小余为0.8118日。因此,这一年的历取冬至时刻是600年12月18日19时29分。
γ2不足整日数的部分为0.4274日,它与历取冬至小余0.8118日两者之和大于1日,则土星定见时刻与其前一个冬至所在日夜半的时距约是339.2391日。由此推算出土星定见日期是601年11月22日。
第4步:求公元600年冬至时刻之后的土星定见所在日夜半的黄经。
(1)求公元600年历取冬至时刻的太阳黄经
方法是在理论冬至时刻的太阳黄经270°的基础上,增减在历取与理论冬至时刻差期间太阳运行的度数。《皇极历》依据日行盈缩将回归年以“二分”为界分为两部分,“秋分后春分前为盈汎,春分后秋分前为亏总”([21],页1936)。据术文得知冬至每气日数是:

根据步日躔术,得到冬至这一日太阳的中心差值为:

因此,公元600年历取冬至时刻的太阳黄经是:

(2)求公元600年冬至时刻之后的土星定见时刻的黄经
依据“求星见所在度”,得知关键步骤是求太阳在γ2内实际运行度数d。定见时刻入冬至后第22气约第7.5183日,根据步日躔术,得到在γ2内太阳实行度与平行度之差约为0.7518度。由于太阳平行度为每日1度,所以太阳从冬至时刻至定见时刻运行的度数为:
d=γ2-0.7518=338.4274-0.7518=337.6755(度)。
将其结果代入公式(4),即
由此得知土星定见时刻的黄经是226.4620°。
(3)求公元600年冬至时刻之后的土星定见所在日夜半的黄经

(7)
根据第3步所得土星定见时刻与其前一个冬至所在日夜半时距约是339.2391日,可知土星定见小余r′约为0.2391日,且由表1得到土星的初日速度v0为4364/46644(度/日)。将其代入(7)式得到:
由此得知土星定见所在日夜半的黄经是226.4400°。
第5步:求公元600年冬至时刻之后的土星定见所在日至夕始伏每日夜半的黄经。
在第4步计算结果基础上,累加表1土星动态表中的自晨始见至夕始伏土星的每日行度,得到定见之后每一日夜半的土星黄经值,其结果如下文表2中的“历取黄经”一栏所示。
3 《皇极历》外行星计算精度及分析
3.1 《皇极历》外行星位置计算精度结果
上一节中我们以土星为例,利用《皇极历》五星推步方法已得到公元600年冬至之后的土星一个会合周期自晨始见至夕始伏每日夜半的历取极黄经,所以将其与理论黄经求差值的做法(历取黄经-理论黄经),即可算得土星这个周期的黄经绝对误差(8)行星视位置的极黄经和真黄经的确有一些差别,但由于外行星运行轨道与黄道的夹角较小,因此这两者的差别就非常小,且与行星理论的系统误差比较,外行星的这些误差目前可以暂时忽略。参见参考文献[1]。。
土星的理论黄经结果可以通过天文软件Skymap提取并计算得出,宁晓玉的研究表明Skymap软件满足古天文研究数据的精确度和稳定性,是准确可靠的天文软件[28]。所提取的理论数据是土星自601年11月22日定见之后341日的每日夜半时刻赤经和赤纬值,需要将其换算到对应的黄经值,其结果如表2中的“理论黄经”一栏所示。

表2 《皇极历》以601年11月22日为土星定见的会合周期晨始见至夕始伏位置精度
上一节已得到公元600年冬至之后的土星定见日期是601年11月22日,其儒略日序号数是1940899。这里限于篇幅仅给出该会合周期自晨始见至夕始伏每间隔20日的土星黄经数值。将《皇极历》五星推步算法得到的历取黄经与理论黄经求差值,以推算土星这个周期的黄经绝对误差,如表2所示。
根据表2最后一栏“黄经误差”,以每日结果绘制土星黄经绝对误差散点图,如图4所示。经统计分析,土星数据量有341个,黄经误差绝对值的平均值为1.46°,误差绝对值的最大值为2.51°。

图4 601年11月22日定见至始伏土星黄经绝对误差散点图
以同样方式分别计算出木星开皇二十年冬至后定见发生于601年6月2日,火星定见发生于601年11月29日。分别绘制出木星和火星在这个会合周期内自晨始见至夕始伏期间的黄经绝对误差散点图,如图5和图6所示。

图5 601年6月2日定见至始伏木星黄经绝对误差散点图
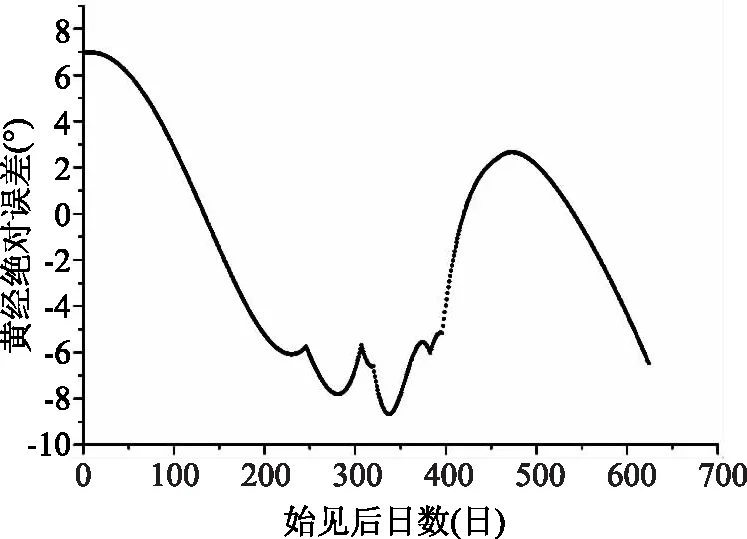
图6 601年11月29日定见至始伏火星黄经绝对误差散点图
经统计,木星数据量有363个,黄经误差绝对值的平均值为1.83°,误差绝对值的最大值为3.12°;火星数据量有624个,黄经误差绝对值的平均值为4.21°,误差绝对值的最大值为8.67°。
为了更深入全面探讨《皇极历》外行星计算精度,接下来将推算《皇极历》制成之后约30年长时段内木星、火星和土星在每日夜半的黄经,并将其与行星理论黄经比较,以得到绝对误差结果。对于木星,计算了开皇二十年冬至后的28个完整会合周期自晨始见至夕始伏的每日夜半位置,数据量为10165个;对于火星,计算了15个完整会合周期的每日夜半位置,数据量为9204个;对于土星,计算了29个完整会合周期的每日夜半位置,数据量为10231个。
根据计算结果分别绘制出木星、火星和土星的黄经绝对误差散点图,如图7—9所示。图中的纵坐标表示行星黄经绝对误差,单位为“°”;横坐标表示从公元600年冬至之后外行星首次定见所在日的夜半起算的日数,单位为“日”。图7中的横坐标始于601年6月2日夜半,图8始于601年11月29日夜半,图9始于601年11月22日夜半。

图7 《皇极历》木星黄经绝对误差散点图

图8 《皇极历》火星黄经绝对误差散点图

图9 《皇极历》土星黄经绝对误差散点图
从图7—9可以看出,外行星的黄经绝对误差在约30年内呈现出周期性的变化。然而,在此之中火星有两个会合周期的误差比较反常。通过查验,这两个周期的晨始见分别处于白露、秋分两气,处于这两气的修正方案是“白露至寒露,初日行半度,四十日行二十度”。已在第1章中论述火星动态描述时,指出此处“半度之行”是对火星晨始见位于“白露至寒露”段内的二次修正,日率减去40日,度率减去20度。若不考虑术文中的“初日行半度”的修正,可绘制出火星黄经绝对误差散点图,如图10所示。

图10 《皇极历》火星黄经绝对误差散点图(不修正“初日行半度”)
如图10,若不考虑火星晨始见位于“白露至寒露”段内“初日行半度”的修正,这两个反常周期(图8)的误差会大幅度减小,且与前后会合周期的误差衔接度更好。
因此,根据以上分析,《皇极历》外行星计算精度可由表3中的相关数据反映。
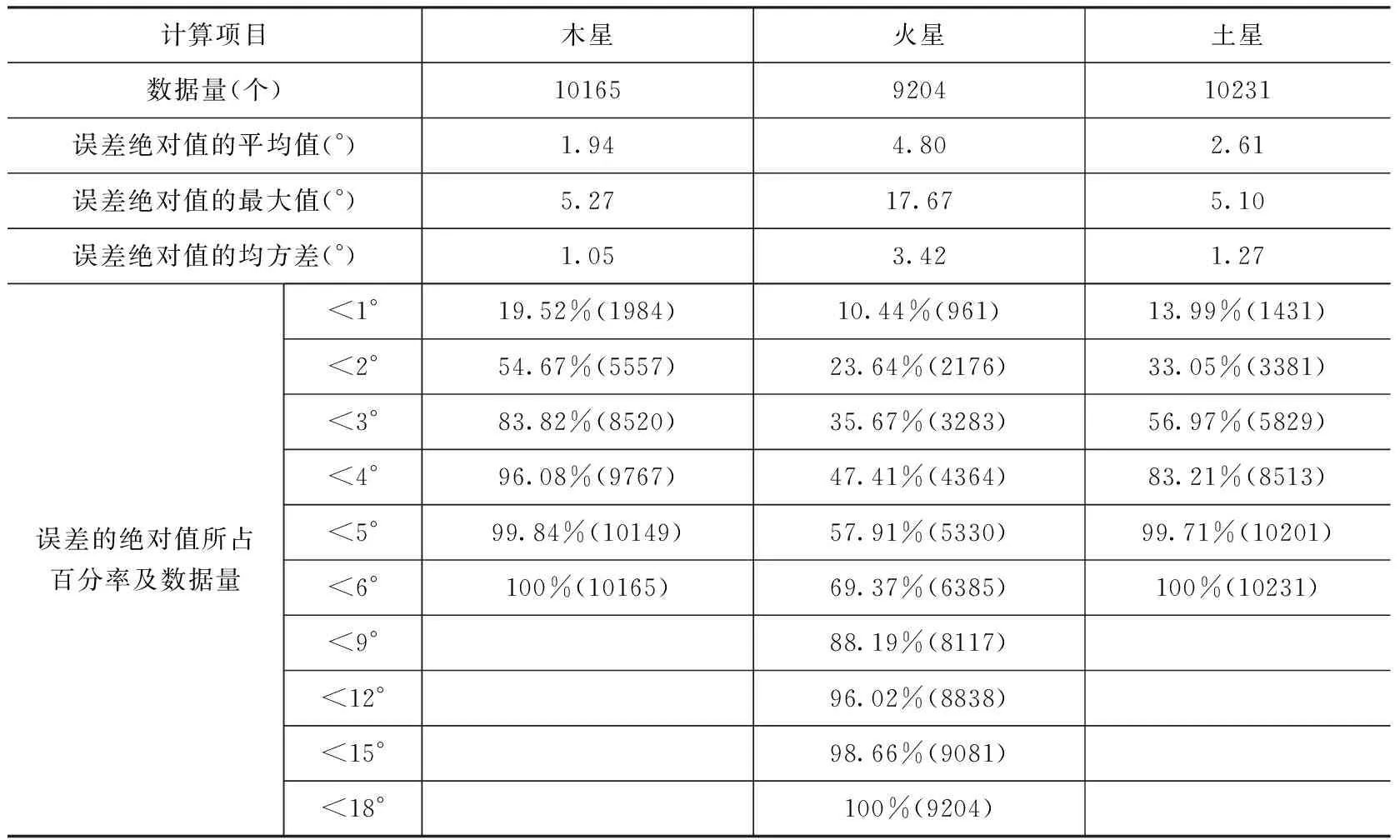
表3 《皇极历》601—630年外行星计算精度(9)表3中火星计算精度结果均为不考虑“初日行半度”情况下所得。
印度天文学著作《五大历书汇编》成书于6世纪中叶,其中的《宝莉莎历数书》与中国传统历法处理行星运动的方式相同,即以代数方法计算行星的位置。唐泉对《宝莉莎历数书》中的行星运动作了深入研究并给出外行星及金星的计算精度[11],外行星计算精度数据摘录于表4。通过比较,《皇极历》中推算外行星黄经误差精度相比《宝莉莎历数书》要稍微高一些。

表4 《宝莉莎历数书》行星计算精度
3.2 影响《皇极历》外行星位置精度的原因分析
根据上述对《皇极历》行星推步算法的解读分析,不难看出,定见时刻被视为行星在一个会合周期上的关节点,再由太阳位置及见去日推算行星定见时刻的位置,最后以行星每日的行度累加,即可得到行星任意一日的位置。可见,行星定见时刻的推算,以及行星在一个会合周期内自晨始见至夕始伏的每日行度都有可能影响到《皇极历》外行星位置计算精度。接下来,从这两方面展开探讨。
一方面,有必要对行星在约30年时段内每次定见时刻的精度进行分析。依据《皇极历》行星推步算法得到开皇二十年冬至后约30年内木星、火星和土星各完整会合周期的历取定见日期,以及由中国黄道星空天文软件所得理论定见日期(10)“中国黄道星空”是刘次沅专门为研究中国古代天象记录而开发的一款天文软件,它可以计算并演示日、月、五星在黄道天区的位置和运动。此处的“理论定见日期”就是通过《皇极历》所给外行星“见去日”常数,进而借助该软件推算这一天象发生的日期。,如表5所示。

表5 《皇极历》601—630年木星、火星和土星定见日期
表5中结果表明木星历取定见日期与理论定见日期的最大误差是6日,平均误差约为2日;火星的最大误差是41日,平均误差约为21日;土星的最大误差是5日,平均误差约为3日。可见,《皇极历》推算外行星定见时刻的计算误差中火星最大,木星和土星基本相当。
另一方面,我们对外行星在一个会合周期内自晨始见至夕始伏的速度进行分析。根据表2的计算结果,可绘制以600年11月22日为土星定见的一个会合周期内的理论速度与历取速度,即呈现出开皇二十年冬至之后土星在一个会合周期内的运动状态。如图11所示。

图11 土星理论速度与历取速度图示
《皇极历》中的土星在一个周期内的运动状态被分为前顺行、前留、逆行、后留和后顺行这五个段目,且顺行与逆行的历取速度均以匀速运动给出,如图11所示。对比理论速度曲线可以看出,土星的理论速度实际在每时每刻都是改变的。历取速度划分的段目较少,很难达到与理论速度较好拟合。此外,历取速度在前留、后留这两段目各占39日,而实际理论速度中“留”却仅是存有一瞬间的状态。因此,《皇极历》对土星一个周期内各段目的运行状态描述也是影响土星计算精度误差的一个重要因素。
以同样的方式,绘制出开皇二十年冬至之后木星和火星在一个会合周期内的理论速度与历取速度,如图12和图13所示。
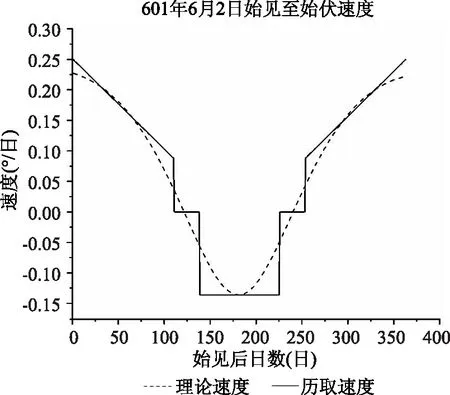
图12 木星理论速度与历取速度图示

图13 火星理论速度与历取速度图示
值得注意的是,与木星和土星不同,图13中所呈现的火星在一个会合周期内的理论速度与历取速度并不对称,换言之,其晨始见的速度与该会合周期夕始伏的速度不相等。从理论速度曲线上同样反映出这一现象,且历取速度与之拟合较好。如图14所示,我们给出更大的时间范围内速度拟合曲线,即约公元600—630年火星15个会合周期内晨始见至夕始伏期间运行理论速度与历取速度图示。
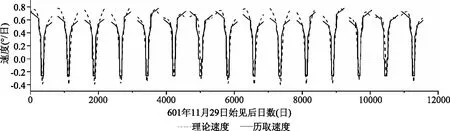
图14 《皇极历》火星公元601年11月29日夜半后每日理论速度与历取速度图示
《皇极历》的火星历取速度之所以能达到这样好的效果,其原因在于它设计火星前疾段和后疾段运动状态时的巧妙算法,以一个会合周期中前疾初日与后疾初日所值节气,来分别规定火星在这两个段目运行的日率和度率。
4 结论
本文通过对《皇极历》外行星入气加减差、动态描述及五星推步算法构建思路的解读,并结合上述分析讨论,得出下面几点结论:
(1)根据表3中的数据,得知对《皇极历》外行星而言,木星和土星黄经误差绝对值的最大值分别是5.27°和5.10°,误差绝对值的平均值分别是1.94°和2.61°。这表明《皇极历》中木星和土星的计算精度大体相当,而火星黄经计算误差要比木星和土星大得多。火星黄经误差绝对值的最大值是17.67°,约是木星和土星黄经最大误差的3倍还要多,误差绝对值的平均值也达到4.80°。此外,通过对外行星约30年中的每个定见日期的误差分析,如表5,同样得到火星的定见日期误差最大,木星和土星误差相当且较火星小很多。这是因为火星在三个外行星中,它的轨道偏心率最大、周期长、速度快,因而火星的计算相对木星和土星要更困难一些。
(2)《皇极历》讨论火星“前疾”段的日率和度率时,附加修正法则所提到的“半度之行”,这一项修正对火星黄经计算精度的提高似乎没有发挥正面作用,如图8和图10所示。引入“半度之行”修正的火星黄经误差绝对值的最大值高达31.49°,误差绝对值的平均值是6.65°;而未考虑“半度之行”修正的火星黄经误差绝对值的最大值是17.67°,误差绝对值的平均值是4.80°。可看出从精度方面考察,这个算法显得多余。但是从初唐《戊寅元历》《麟德历》这两部历法对“半度之行”的论述分析而言,其涵义就是对原有日率和度率的二次修正,理解上无误。因而关于“半度之行”的合理性问题还需要作进一步探讨。
(3)《皇极历》外行星黄经绝对误差散点图呈现周期性变化的规律,与其公转周期基本吻合,如图7—10所示。文章中所讨论自公元600年冬至之后首次始见的当日夜半起算约12000日时间段内,大约包含了2.7个木星公转周期、1.1个土星公转周期、17.5个火星公转周期。木星和土星黄经绝对误差的变化规律与它们的公转周期比较吻合,而火星由于其公转周期较短,其黄经绝对误差变化不太容易与公转周期对应。然而,火星呈现出七个会合周期循环规律性的波动趋势,这与火星的大冲周期更为匹配。
(4)由于目前隋代之前的历法行星计算精度的研究甚少,本人所在项目组的其他成员提供了一些未发表的魏晋南北朝时期历法中外行星误差计算精度的初步结果,得知这时期木星和土星的黄经误差绝对值的最大值达到十几二十多度,火星更是有高达四五十度的误差。可见,《皇极历》在引入太阳和行星不均匀运动修正算法之后,确实在很大程度上改善了其行星计算水平。虽然隋代及唐初时期历法中的“入气加减差”和“五星动态表”均属于基于经验性观测的数值算法系统,但是这项研究也进一步表明古代历法家在探索行星运动理论、设计数值算法逐渐逼近真值的过程中,不懈努力的精神是值得肯定和学习的。
致 谢感谢两位匿名审稿专家提出宝贵的修改建议。论文写作过程中还得到了北京天文馆古观象台杨帆老师提供的材料和帮助,在此表示衷心感谢!

