河南地区降水量和云量与地面太阳短波辐射的关系

李张群 肖子牛 丁煌 崔方

1 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点室验室，北京 100029

2 中国科学院大学地球与行星科学学院，北京 100049

3 中国电力科学研究院有限公司，南京 210003

1 引言

太阳辐射是地球表层能量的主要来源，太阳能因其绿色环保的特点，被认为是未来发展中具有潜力的可再生能源。随着人类社会经济的发展，化石能源燃烧释放的大量CO2造成全球气候变化已经成为不争的事实。光伏发电具有资源分布广泛和安全清洁等优势，为积极应对气候变化，光伏发电产业的发展越来越受到重视，开发利用太阳能被认为是解决能源危机与气候问题的有效途径之一（UNDP, 2000; 王 峥 和 任 毅, 2010; Creutzig et al.,2017）。近十年来，中国的光伏发电产业迅猛发展，2010 年我国太阳能光伏装机容量还不足1 GW（1 GW=109W），而2017 年底就已达到130 GW。未来我国太阳能面板的光伏装机容量还将进一步大幅增长，到2050 年，风能和太阳能将成为中国新能源系统的绝对主力（郑磊和陈醒, 2018）。由于光伏系统的发电量首先取决于可利用的太阳辐射量，即到达地表的太阳辐射，所以太阳辐射量的研究越来越受到重视（贾东于等, 2020）。

我国河南省位于（31°23′N～36°22′N，110°21′E～116°39′E）之间。河南省太阳能总辐射量和年平均日照时间处于国内中等水平，比我国青藏高原和西北等地低，但比四川、贵州等地高得多。河南省所处的中纬度地区天气复杂多变，到达地面的太阳短波辐射受到降水、云量、湿度等气象要素的影响，使光伏发电输出具有明显的日、季节变化以及不连续性和不确定性（崔洋等, 2013）。近年来，河南地区太阳能光伏可再生能源的开发有了很大发展，对光伏发电量的预报日益成为光伏企业的基础需求。目前，全国太阳辐射观测站点少，对太阳辐射的研究分析比较缺乏，业务发展较慢（代倩等, 2011）。虽然云量、降水等气象要素的变化会对到达地面的太阳短波辐射产生很大的影响，但目前太阳辐射预报主要还是天文周期的变化评估，基本没有考虑气象要素的影响。而中国的天气预报系统已比较完善，各地都能方便及时地获得天气预报产品。因此，分析气象要素对光伏的影响，建立气象要素与地面太阳短波辐射的关系模型，可以帮助光伏企业方便地通过气象要素的预报来获取光伏发电量的变化信息。

虽然已有研究结合历史发电量数据和气象数据分析了影响光伏发电量的各项因素（陈昌松等,2009），但是对光伏发电量与气象因素之间的相关性没有进一步研究。代倩等（2011）通过光伏发电量与气象因子之间的相关性分析，提出采用气温、湿度等气象因子组合代替太阳辐照度，建立无辐照度发电量短期预报模型。但事实上，太阳辐照度受云 量 的 影 响 最 大（Kern et al., 1989; Ehnberg and Bollen, 2005），低云量是影响地面接收太阳辐射的关键参数（Stjern et al., 2009; 郑志远等, 2014; 马丹阳等, 2020；蒋俊霞等, 2020）。此外，Chiacchio and Vitolo（2012）的研究发现云量对欧洲地区地面太阳短波辐射的影响存在明显的季节差异和区域差异。我国地气系统短波辐射云强迫及其敏感性系数与总云量也有较好的关系，且季节变化明显，说明短波辐射云强迫的地理分布与总云量有很好的匹配关系（刘艳等, 2000）。Wan et al.（2021）分析了新疆云量和太阳能资源分布的相关关系，指出新疆夏季太阳辐射主要受云量的影响，而冬季还受气溶胶等其他因素的影响。此外，水汽是大气中最活跃的组分，其对太阳辐射有吸收作用（申彦波等,2008）。并且，相对于温度、相对湿度和气压，水汽对太阳辐射更为敏感（刘严萍, 2020）。降水量是天气预报系统中可预报性较强的气象要素，降水会直接影响大气中的水汽含量，从而对地面太阳短波辐射产生影响。因此，本文将分析河南省有云日总云量（Total Cloud Cover, TCC）和有降水日总降水量（Total PREcipitation, TPRE）对地面太阳短波辐射（Surface Solar Radiation Downwards, SSRD）的影响，通过建立总降水量和总云量与地面太阳短波辐射之间的关系模型，对太阳短波辐射进行拟合，为光伏发电日变化的评估预报提供参考。

2 资料和方法

2.1 资料

本文采用欧洲中期天气预报中心（ECMWF）提供的ERA5 再分析资料，资料起始时间为1979年（2020 年已发布将时间范围提前至1950 年的初步版本），并持续更新至实时5 d 以内。其空间分辨率为31 km（约为0.28°），时间分辨率为逐小时。本文使用了2009～2020 年时间段的再分析数据，水平方向上已插值为0.25°（纬度）×0.25°（经度）的规则网格（Hersbach et al., 2020），变量包括SSRD、TCC 和TPRE。本研究关注河南省总云量和总降水量与地面太阳辐射的日间关系，因此首先计算了原始资料的逐日平均。文中春季为3～5 月，夏季为6～8 月，秋季为9～11 月，冬季为12 月到次年2 月。

为了验证ERA5 再分析资料在河南省的可信度，本文采用国家气象信息中心提供的中国地面台站观测资料日值数据集V3.0（http://data.cma.cn/[2019-04-12]）对2009 年5 月和10 月河南省平津观测站（34.83°N，112.43°E）ERA5 再分析资料的SSRD与观测资料中辐射的逐日演变进行对比分析，并计算两者相关系数，结果显示ERA5 再分析资料中SSRD 的变化与量级都与观测资料非常一致，2009年5 月和10 月再分析资料与观测资料的相关系数分别为0.86 和0.78，均通过置信水平为99.9%的显著性检验，说明ERA5 再分析资料与观测资料的SSRD 具有一致性。并且，已有对中国地区ERA5降水资料与气象站观测降水资料的对比分析指出虽然ERA5 降水与观测资料之间存在偏差，但能较好地反映观测降水时空演变的总体特征，总体而言两种降水数据的线性相关程度较好（Hu and Yuan,2020; 孙赫等, 2020; 张佳鹏等, 2021）。因此，本文认为使用ERA5 再分析资料描述河南省2009～2020 年总降水量的变化是可信的。

2.2 方法

拟合分析是气象、气候统计分析中常用的一种方法，用于提取两个或多个变量间的相互关系，用一条直线代替样本点，以达到预测的作用。由于气候因子间多近似线性关系，因此，本文使用一元线性拟合和二元线性拟合来探讨TPRE 和TCC 与SSRD 的关系（黄嘉佑, 2004）。以一元线性拟合为例，两个相关的变量X（x1，x2，...，xn）和Y（y1，y2，...，yn）由如下的拟合方程来表达：

其中，a和b为拟合系数，使用最小二乘法对拟合系数进行估计，拟合系数a、b可以直接表示为

n表示变量X和 变量Y的样本数量，x和y分别表示变量X和变量Y的算术平均值。

两个变量X1（x11，x12，...，x1n）和X2（x21，x22，...，x2n）和另一个相关变量Y（y1，y2，...，yn）之间的拟合关系由如下的二元线性拟合方程来表示：

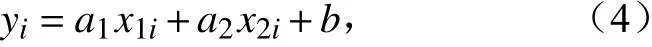
其中，a1、a2和b为拟合系数，类似公式（2）和公式（3），同样使用最小二乘法对拟合系数进行估计。

3 不同季节总降水量和地面太阳短波辐射的关系

图1为2009～2018 年河南省四季的有降水日总降水量（TPRE）和地面太阳短波辐射（SSRD）的空间相关关系。4 个季节SSRD 和TPRE 均为显著的负相关关系，相关系数通过置信水平为99%的显著性检验，但相同区域不同季节的相关程度不尽相同。其中，SSRD 和TPRE 夏季的整体空间相关最好（图1b），冬季次之（图1d），春季和秋季相对夏季和冬季相关较弱（图1a、1c）。从相关系数的空间分布来看，河南省各个季节SSRD和TPRE 相关系数的大小均为西南部较大，向东北逐渐减小。由于河南省西部海拔高于其东北部，西部山区降水主要受季风环流和高大山地地形的综合作用，易发生局部短时强降水，而东部平原地区主要受季风环流影响，东西部降水差异较为明显（沈秉璐, 2019）。并且，河南省东部城市集群比西部更多，建筑面积增加会导致气溶胶光学厚度显著增加（段彦博等, 2017），而西部山区植被覆盖度较高，植物的滞尘效应在一定程度上有助于缓解气溶胶的污染且人为气溶胶颗粒物较少，抑制了气溶胶光学厚度的上升（何沐全等, 2017; 张磊等, 2017）。东部的SSRD 可能受更多其他因素（例如，城市化引起的气溶胶、浮尘等）的影响。因此，不同季节TPRE 与SSRD 的相关系数自西南向东北递减的空间分布特征可能与河南省内地形差异引起东西部降水不同以及城市集群的空间分布造成河南省东西部气溶胶光学厚度的不同有关。

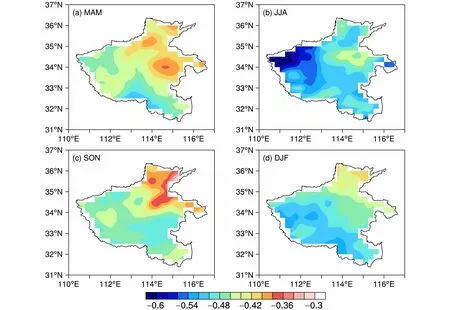
图1 河南省2009～2018 年（a）春季（MAM）、（b）夏季（JJA）、（c）秋季（SON）、（d）冬季（DJF）逐日总降水量（TPRE）和地面接收的向下短波辐射（SSRD）的空间相关系数（均通过99%的信度检验）Fig. 1 Correlation between the daily Solar Shortwave Radiation Downwards (SSRD) and Total PREcipitation (TPRE) in Henan Province in (a) spring(March-May, MAM), (b) summer (June-August, JJA), (c) autumn (September-November, SON), and (d) winter (December-February, DJF) from 2009 to 2018 (all passed the 99% confidence level)

在分析河南地区SSRD 和TPRE 之间的线性拟合关系时，由于TPRE 具有较强的偏态分布特征，因此，将TPRE 取对数与SSRD 进行拟合。河南省不同季节日平均的SSRD 和TPRE 对数之间的散点图表明，4 个季节SSRD 和TPRE 的对数均显著负相关，相关系数都通过置信水平为99.9%的显著性检验（图2）。从拟合优度R2可以看出，夏季SSRD 和TPRE 对数的拟合关系最好，拟合优度为0.467（图2b），是四季中两者拟合优度最大的季节。春季次之，拟合优度为0.363；秋季拟合优度最弱。从4 个季节的拟合结果来看，夏季SSRD受TPRE 的影响最大，其他3 个季节SSRD 与TPRE 的关系也非常密切，TPRE 对SSRD 的预测有一定的参考价值。

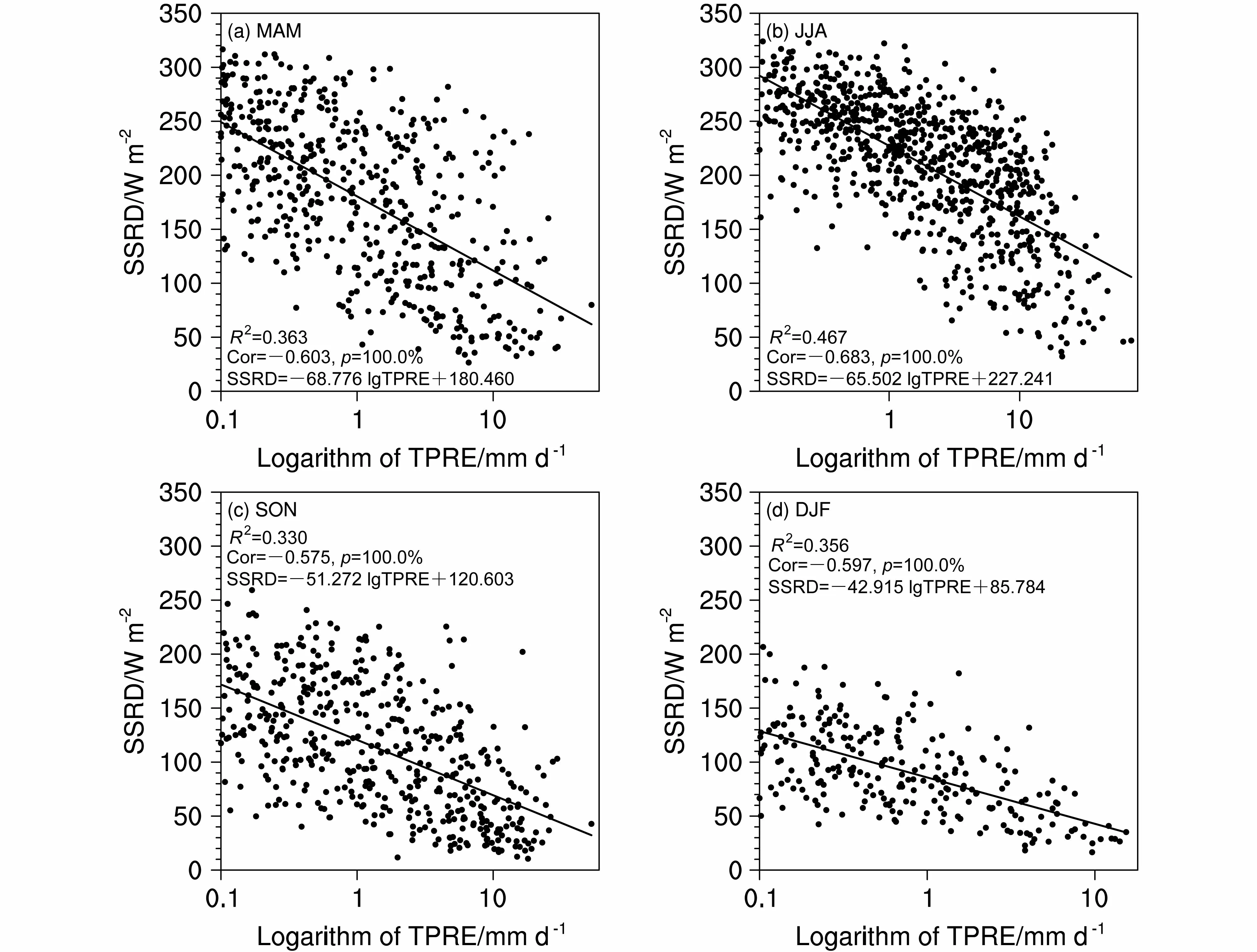
图2 河南省2009～2018 年（a）春季、（b）夏季、（c）秋季、（d）冬季有降水日TPRE 的对数和SSRD 之间的散点图。黑色实线表示两者之间的线性拟合，并给出了拟合方程、拟合优度R2、相关系数（Cor）和相关系数显著性检验的置信水平（p）Fig. 2 Scatterplots of the logarithm of TPRE against SSRD in Henan Province in (a) MAM, (b) JJA, (c) SON, and (d) DJF from 2009 to 2018. The solid black line shows the linear fitting between the logarithm of TPRE and SSRD. The linear fitting equation, R2, correlation coefficient, as well as the confidence level of the significant test are shown

4 不同季节总云量和地面太阳短波辐射的关系

为了分析总云量和地面太阳短波辐射的关系，图3 展示了2009～2018 年河南省春夏秋冬有云日TCC 和SSRD 之间的空间相关。从图中可以看到，各季节日平均SSRD 和TCC 显著负相关，相关系数均通过置信水平为99%的显著性检验，但相关性强弱的空间分布不尽相同。其中，秋季两者的空间相关最为密切（图3c），春季次之（图3a），冬季最小（图3d）。各季节相关系数大小的空间分布差异体现为：春季河南省SSRD 和TCC 相关系数大小的空间分布西南较大，东北相对较小（图3a），夏季相关系数从西到东减小（图3b），秋季和冬季SSRD 和TCC 的相关系数均为南部较大，北部相对较小（图3c、3d）。由于纬度的高低直接影响太阳辐射的大小，一般纬度越低，辐射越强（朱乾根等, 2007），这可能造成TCC 与SSRD 的空间关系存在南北差异。此外，夏季降水最丰富，SSRD 受河南省内降水东西部差异的影响可能比其他季节更大，因此夏季TCC 与SSRD 的相关关系存在东西差异。

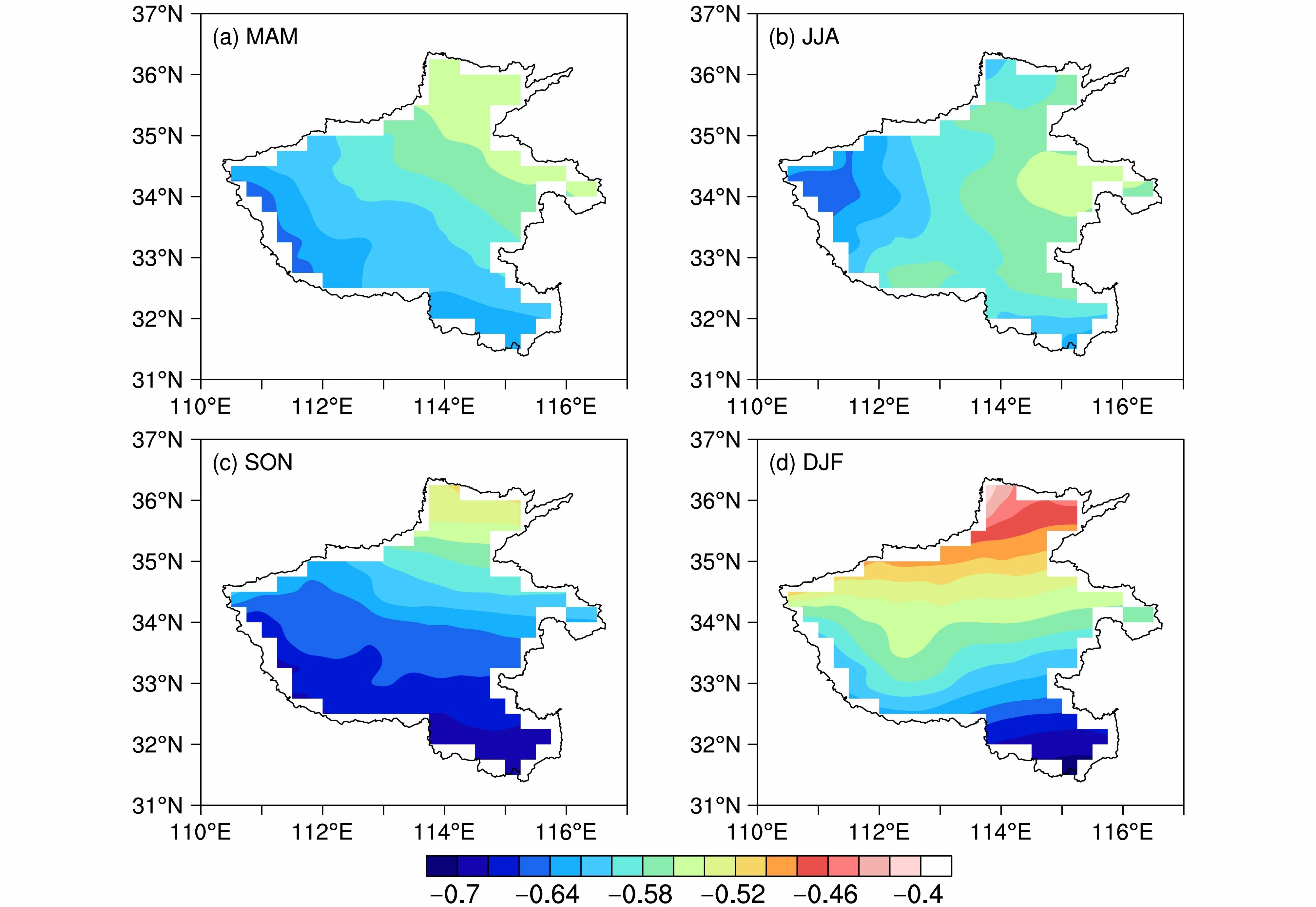
图3 同图1，但为逐日TCC 和SSRD 的空间相关系数Fig. 3 Same as Fig. 1, but for correlation between the daily SSRD and total cloud cover (TCC)

图4为河南省春夏秋冬分别的日平均SSRD 和有云日TCC 之间的散点图，用来分析SSRD 与TCC 的线性拟合关系。从图中可以看到，不同季节的拟合关系存在差异，其中，秋季SSRD 和TCC 的拟合关系最好，两者的拟合优度为0.439。总体上，河南省春夏秋冬SSRD 与TCC 都有较好的对应关系，春季两者的拟合优度为0.402，夏季拟合优度是0.382，冬季0.363。河南省4 个季节逐日SSRD 与TCC 均呈显著负相关关系，相关系数通过置信水平为99.9%的显著性检验。以上分析结果有助于建立基于通常天气预报的光伏发电资源的预报指标，这与Wan et al.（2021）的结论一致，利用云量对辐射进行校正和预报，有助于提高太阳能发电的预报精度。

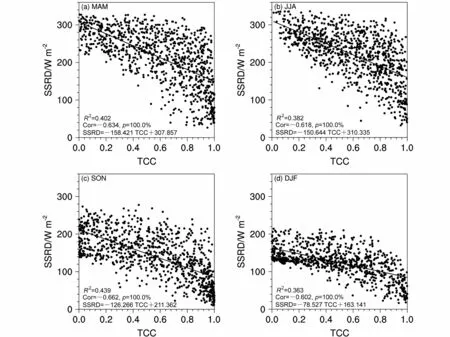
图4 同图2，但为有云日的TCC 和SSRD 之间的散点图Fig. 4 Same as Fig. 2, but for scatterplots of the TCC against SSRD

5 地面太阳短波辐射与总降水量和总云量的关系模型

由以上分析可知，河南省的TPRE 和TCC 都分别对SSRD 有显著的影响，但不同季节存在一定差异。对河南省2009～2018 年季节平均的TPRE、TCC 和SSRD 的空间分布特征进行分析，发现春季、夏季和冬季TPRE 从河南省东南向西北逐渐递减，秋季从西南到东北逐渐递减。春季、夏季和秋季TCC 从河南省西南向东北逐渐减小，冬季TCC从东南向西北逐渐减小。而春季和夏季河南省北部SSRD 最大，向南逐渐减小；秋季，河南省东北部SSRD 最大，向西南减小；冬季，河南省西北部SSRD 最大，向东南方向逐渐减小（图略）。由此可见，各季节河南省SSRD 的空间分布特征并不与TPRE 或者TCC 的空间分布特征完全对应，说明SSRD 并不是受单一气象要素影响的，采用TPRE 和TCC 两个气象要素来拟合SSRD 可能会有更好的效果。因此，接下来使用二元线性回归模型对各季节SSRD 分别进行拟合，基于公式（4），使用最小二乘法计算出各回归系数，构建出春季、夏季、秋季和冬季分别基于河南省TPRE 和TCC对SSRD 进行拟合的二元线性回归模型，其中SSRD*为重建的地面太阳短波辐射。

为了验证本文构建的二元线性回归模型，对2019 年的SSRD 进行回归，2019 年春夏秋冬逐日变化的TPRE 和TCC 分别作为输入，计算出4 个季节的SSRD*，再分别使用3 个统计评价指标对SSRD*和ERA5 资料中实际的SSRD 进行比较，统计指标分别为均方根误差（RMSE）、平均绝对误差（MAE）和相关系数。如图5 所示，二元回归模型对2019 年春夏秋冬的SSRD 都分别有较强的拟合能力，各季节SSRD*和实际的SSRD 均有显著的正相关关系，且相关系数较大，通过置信水平为99.9%的显著性检验：春季两者相关系数为0.450，夏季为0.670，秋季为0.695，冬季为0.606。从拟合优度R2的数值上来看，秋季拟合最优（R2=0.483， 图5c），夏季次之（R2=0.450，图5b）。从春季到秋季，SSRD*的MAE 随季节减小，春季到夏季RMSE 也减小，而相关系数在增加，这说明春季到秋季，河南省有云日TCC 和有降水日TPRE 对SSRD 的拟合优度增加。由于本文讨论有降水日的情况，资料中夏季与秋季相比，夏季有降水日更多，因此实际参与计算的样本量夏季比秋季多，从散点沿拟合线分布的密集程度来看，夏季拟合同样很好，SSRD*和实际SSRD 的偏差较小。可以看出，不同季节虽然样本数量有差异，但是显著的正相关关系都存在，且拟合优度都较优，证明同时考虑TPRE 和TCC 构建的二元线性回归模型对河南省SSRD 有比较强的拟合能力。

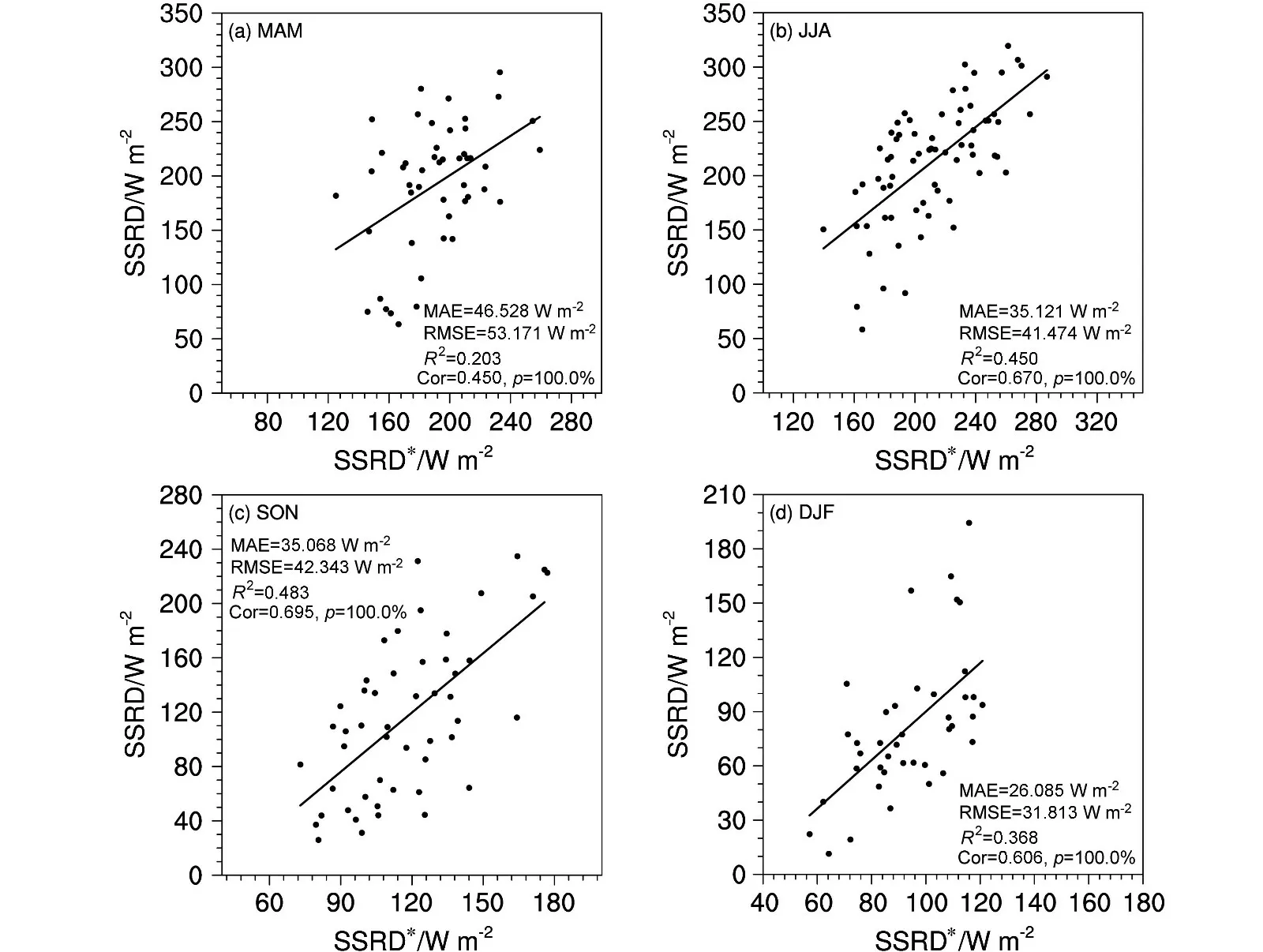
图5 2019 年（a）春季、（b）夏季、（c）秋季、（d）冬季基于TPRE 和TCC 回归得到的SSRD*与实际SSRD 的散点图。黑色实线表示两者之间的线性拟合，并给出了SSRD*与实际SSRD 的拟合优度R2、相关系数（Cor）、相关系数显著性检验的置信水平（p）、均方根误差（RMSE）和平均绝对误差（MAE）Fig. 5 Scatterplots of the SSRD* against the actual SSRD in (a) MAM, (b) JJA, (c) SON, and (d) DJF of 2019. The solid black line shows the linear fitting between the SSRD* and actual SSRD. The R2, correlation coefficient as well as the significance test’s confidence level, root-mean-square error,and mean absolute deviation, that between the SSRD* and actual SSRD are also shown

6 总结与讨论

通过对河南省2009～2018 年不同季节日平均地面太阳短波辐射（SSRD）与有降水日总降水量（TPRE）和有云日总云量（TCC）分别的相关关系进行分析，并进一步基于TPRE 和TCC 对河南省SSRD 进行拟合，得出以下结论：

（1）河南省逐日平均SSRD 分别与TPRE 和TCC 均为显著负相关关系，但不同季节其相关关系的显著性不同。SSRD 与TPRE 和TCC 相关系数的空间分布在各季节不尽相同。

（2）河南省SSRD 分别和TPRE 的对数、TCC之间均有较好的拟合关系，其中，夏季SSRD 和TPRE 的对数的拟合关系最好，秋季SSRD 和TCC 的拟合优度最优。

（3）基于不同季节的TPRE 和TCC 构建的二元线性回归模型对SSRD 有较好的重建效果，该结果有助于建立基于通常天气预报的光伏发电资源的预报指标。

本文的结论可以帮助了解河南省太阳短波辐射与常见气象要素总降水量和总云量之间的关联，这对于光伏发电资源的预报具有重要意义。但本文主要是基于统计分析的结果，并且主要分析了总降水量与总云量和河南省太阳短波辐射的关系，而浮尘、气溶胶等也是影响局地太阳短波辐射的一个重要因素（陈勇等, 2009; 王娜等, 2013），其与太阳短波辐射的关系有待在今后的工作中进一步研究讨论。