洪涝灾害下配电网三维韧性指标评估体系

田 甜，张 骏，叶 樊，刘 超，黎 涛，陶安琪，王 健，杨龙杰，王强钢

(1.国网重庆电力设计院有限责任公司，重庆 404100；2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044)

1 引言

近年来，由山体滑坡、洪涝等自然灾害引起的配电网大规模停电事故逐渐增多，暴露了配电网对低概率、高风险极端事件准备不足、应对能力差的弱点。为提高配电网应对极端灾害的抵抗能力和恢复能力，配电网“韧性”的概念被提出并拓展成为一个新的研究领域[1]。韧性被定义为防御和适应不断变化条件的能力，及承受和中断中快速恢复的能力[2]，评估配电网韧性有助于预防、减少故障损失，帮助配电网迅速恢复到安全运行状态。

目前，国内外针对极端灾害下配电网韧性评估体系已展开广泛研究。文献[3-7]基于台风等极端天气对元件故障率的影响，以配电网负荷缺失面积反映配电网韧性，考虑系统恢复正常时间和灾害过程中故障损失大小，从时间维度实现极端天气下配电网韧性评估。但上述研究未从环境、技术等多维度对配电网韧性进行全面评估。文献[8]基于负荷重要性分级情况，提出一种新的配电网韧性定量评估方法，从经济、社会等维度出发评估配电网灾后恢复能力，但未考虑灾害前期、中期、后期配电网动态变化。文献[9]基于敏感负荷耐受力提出配电网运行韧性评价体系，为电压暂降治理方案评价提供参考，但分布式能源接入、系统自动化水平、极端天气等实际情况未被纳入考虑。文献[10-15]建立了配电网韧性评价体系，将区间层次法与模糊综合评价法相结合，得出最终评价结果，但评价体系中都没有针对极端天气的相关指标，无法应用于自然灾害下配电网韧性评估。截至目前，关注洪涝灾害下配电网韧性评估方法的研究较少。文献[16]提出计及连续风暴和洪水深度不确定性的洪涝灾害下配电网评估指标，指标包含元件脆弱性、可削减负荷等灾前评估状态，但该文献未综合考虑灾中、灾后配电网运行状态进行评估。

针对上述问题，本文建立针对洪涝灾害下配电韧性评估的三维指标体系：①根据洪涝灾害的发展特征及配电网相关特性，提出了三维韧性评估指标体系，从状态、时间、架构三维度实现对配电网韧性的全方位评估；②建立了包括单个节点设备故障率在内的针对洪涝灾害的配电网韧性指标模型，以刻画洪涝灾害下配电网的动态特性；③通过层次分析法对韧性指标评估权重，结合模糊隶属度函数为指标进行评分，实现配电网综合韧性指标求取。本文所提出的评估体系应用于重庆市渝北某农区配电网系统，通过算例分析可以证实该评估体系能够全面、有效反映洪涝灾害下配电网运行状态和抗灾能力，为配电网优化配置和运行提供参考意见和建议。

2 三维韧性评估指标体系构建

评估配电网韧性指标有助于电力系统运维人员精准预测、应对洪涝灾害造成的配电网故障，为关键负荷提供充足可靠电力供应并快速恢复配电网正常供电。以往研究主要关注洪涝灾害的时间维度，难以全面体现配电网韧性评估在规划、调度、监测中的应用功能，也无法准确表现受灾过程中配电网参数动态变化，为制定有效的配电网韧性提升措施造成阻碍。为解决上述问题，本文提出一种针对洪涝灾害下配电的三维韧性评估指标体系(图1)，从状态、架构、时间三个维度拓展指标体系功能效用。

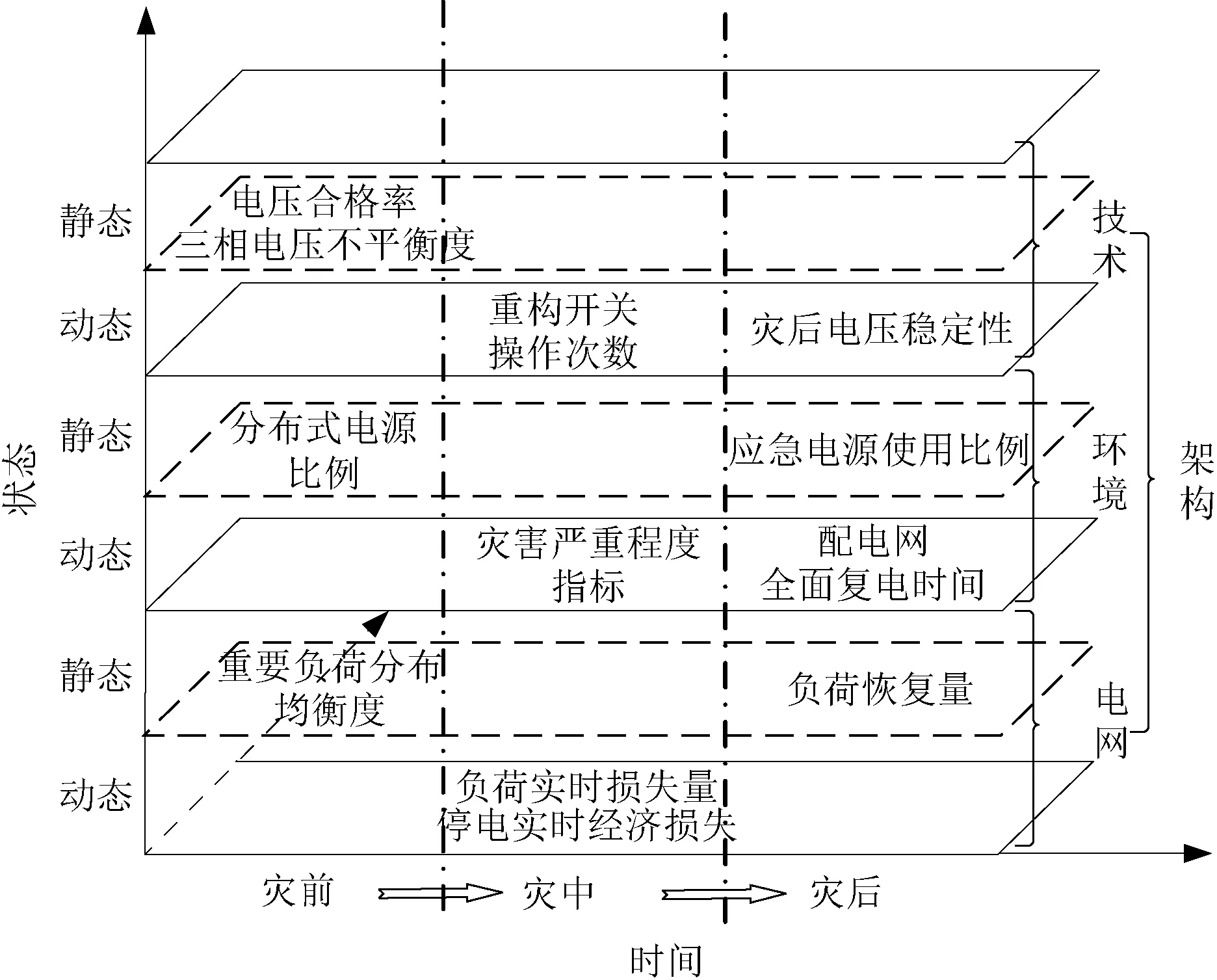
图1 三维韧性评估指标体系示意图

2.1 状态维度

本文指标体系考虑静态、动态两个状态维度。静态指标主要描述灾前配电网运行状态是否健康，柔性负荷、应急电源及无功补偿装置比例是否合理，配电网拓扑结构能否改善；灾后供电恢复是否及时，负荷恢复供电量是否满足需求等。动态指标则聚焦于配电网在洪涝灾害中期发生的实时变化，包括单个节点设备故障率随时间变化、重要负荷损失平均速度等。通过动态与静态指标结合，该体系既可以评估配电网规划与建设，实现配电网韧性横向比较；又可以指导配电网实时调度与恢复决策，分析灾害下电网的实时韧性水平波动，实现配电网纵向比较。

2.2 时间维度

洪涝灾害发生的不同阶段里，配电网韧性水平都会有所不同，一般考虑洪涝灾害前期、中期、后期三个时期。

灾前指标主要用于评估洪涝灾害尚未发生时配电网应对、预防能力，从而为相关部门进行灾害预警和紧急筹措提供参考，这类指标包括能源互联度、分布式电源比例、重要负荷分布均衡度、三相电压不平衡度等。

灾中指标用于反映配电网在洪涝灾害影响下运行实时状态变化，从而为相关部门进行紧急调度提供有效参考，包括负荷实时损失量、灾害严重程度指标、重要负荷损失平均速度等。

灾后指标主要用于评估洪涝灾害过后配电网供电恢复能力及效率，为相关部门制定恢复策略提供参考，包括恢复供电应急电源配置情况、供电恢复方式选择情况、负荷开始恢复响应时间等。

2.3 架构维度

本文的指标体系架构维度主要考虑电网、环境、技术三个方面。

电网维度指标表征的是配电网应对洪涝灾害时自身性能特征，主要包含配电网拓扑结构变化、设备运行情况及负荷分布状况相关评价指标。

环境类指标主要表征洪涝灾害对配电网韧性的影响及新能源发电受环境因素的影响，一般来说洪涝灾害越严重，配电网抵抗外界干扰的能力也就越弱；新能源比例越高，受外部环境影响产生的出力波动也越大，该类指标主要包含洪涝灾害对供电设备的影响及新能源接入的比例。

技术类指标表征配电网未受灾时基础运行状况、可配置应急供电设备数量和可调度恢复供电资源比例，包括应急调度、资源配置、故障分析等。

通过架构维度三类的综合考虑，既可以实现鉴别洪涝灾害影响，为灾害预测提供参考；又能够鉴别电网内部因素，为配电网规划调度、资源优化配置、电力恢复策略制定提供有效指导。

3 配电网韧性指标建模

为便于对韧性指标进行模糊评分，且遵循系统性、一致性、可比性、可测性、独立性原则，本文提出12个涵盖状态、时间、架构维度的归一化评价指标。

3.1 灾前指标

(1)电压合格率：电压合格率表征电力系统在正常运行方式下年度供电电压水平[13]。

(1)

式中，t1为电压越限监测点的电压越限时间；n1为监测点个数。

(2)三相电压不平衡度：三相电压不平衡度是表征三相电压正序、负序、零序分量的指标，体现配电网是否安全运行[13]。

(2)

(3)

式中，FU2、FU0分别为负序、零序电压不平衡度；U1、U2、U0分别为三相电压正序、负序、零序分量均方根值。

(3)分布式电源比例：分布式电源包括风电、光电、生物质能等新能源发电技术，也包括微型燃气轮机在内的应急电源设备，其比例可影响洪涝灾害中期、后期电能调度和应急供电问题[13]。

(4)

式中，SDG为分布式电源容量；S为配电网供电电源总容量。

(4)重要负荷分布均衡度：重要负荷均衡度反映不同配电网负荷分布是否均匀，负荷分布越均衡，重要负荷受灾害影响断电的可能性越小，可靠性越高。

(5)

式中，Ravr为所有馈线负荷率均值；Ri为i馈线上负荷率；n为馈线数目。

3.2 灾中指标

(1)重构开关操作次数：表征洪涝灾害发生时应急控制改变线路拓扑操作开关的次数[17]。

(6)

式中，N为配电网中可操作的开关总数；sj,t为开关j在第t时段0、1变量(0为断开，1为闭合)。

(2)灾害严重程度指标：表征洪涝灾害下单个节点设备故障率与暴雨量关联。

(7)

式中，Q为降雨总量；qp为设备防御等级；ni为设备数量；Qt为t时间降雨量；qs为设备最大耐雨等级；C0为拟合系数，计算如下：

(8)

(3)负荷实时损失量：负荷实时损失量表征洪涝灾害不同时间段负荷断电功率占总负荷功率需求比例[18]。

(9)

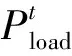
(4)系统停电造成的实时经济损失：表征洪涝灾害中各时段停电造成的经济损失占配电网总损失的比值。

(10)

式中，closs为单位功率负荷损失成本；ctotal为配电网t时间总经济损失。

3.3 灾后指标

(1)灾后电压稳定性：表征洪涝灾害后配电网电压波动情况。

(11)

式中，Vi,t为节点i在不同时间t的电压值；Vn为配电网额定电压值。

(2)应急电源使用比例：表征应急电源配置容量用于灾后供电的比例，比例越高，应急电源利用率越高。

(12)

式中，PDG,iDG、QDG,iDG分别为分布式电源有功、无功出力。

(3)负荷恢复量：表征灾后负荷恢复总功率占负荷需求比例[18]。

(13)

式中，Pre-load为灾后负荷恢复有功功率。

(4)配电网全面复电时间：表征为从洪涝灾害过境期间配电网开始出现负荷失电起，至全部负荷恢复供电所需要的时间，反映了配电网恢复速度。

(14)

式中，tr为全部负荷恢复供电所需时间；t0为配电网开始出现负荷失电时间。

4 基于模糊层次分析法和模糊隶属度函数的指标体系评估

本文提出的三维配电网韧性综合指标评估流程如图2所示。首先结合气象数据及配电网参数，由第3节韧性指标模型得到指标具体数值，而后通过模糊层次分析法(Fuzzy Analytic Hierarchy Process,FAHP)和模糊隶属度函数得到指标权重及隶属区间，进而获得综合指标评估结果。

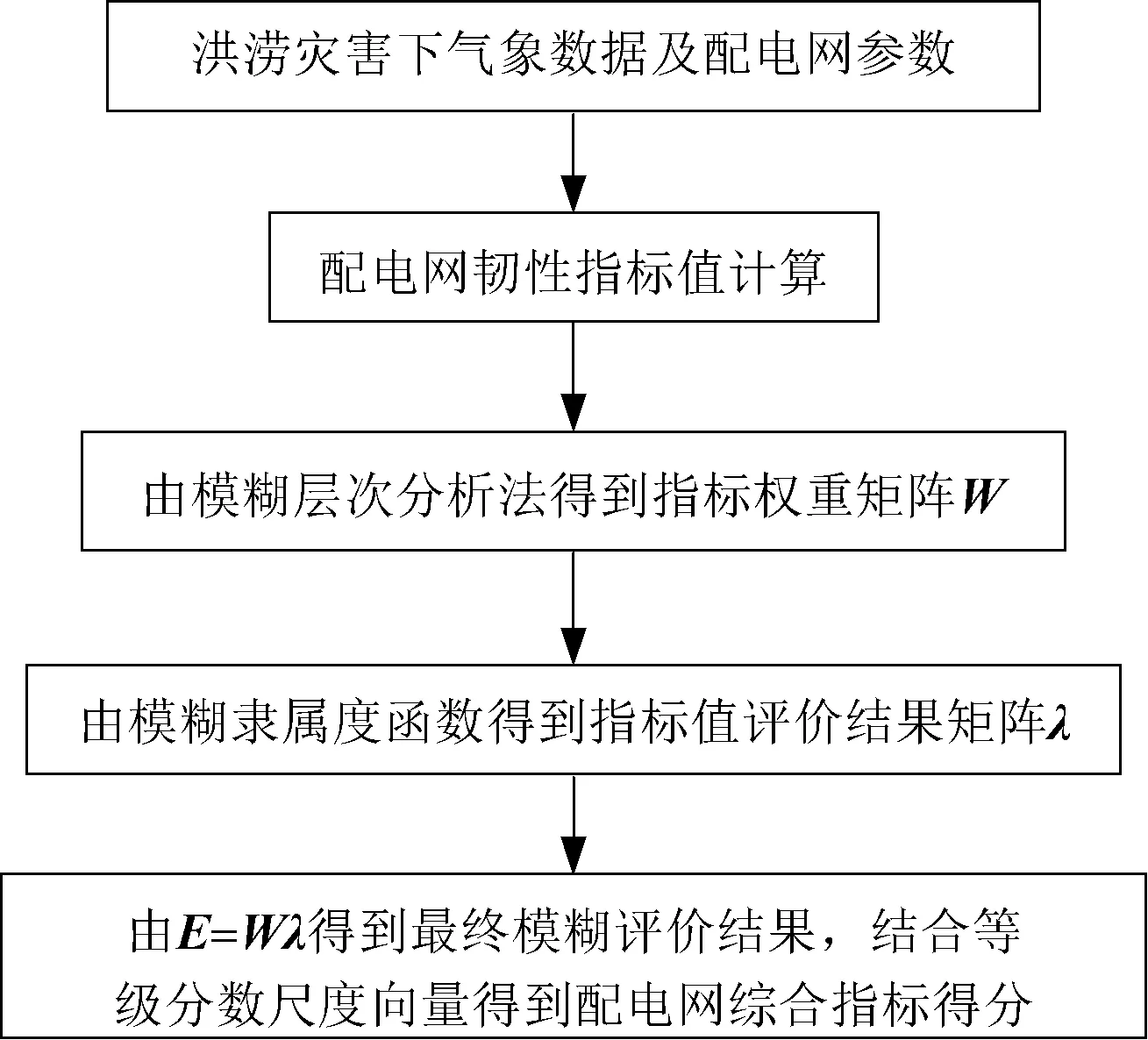
图2 三维韧性指标评估流程图

4.1 模糊层次分析法评估配电网受灾韧性

层次分析法(Analytic Hierarchy Process，AHP)是指将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法[19]。根据层次分析计算综合评估指标的框架示例如图3所示。

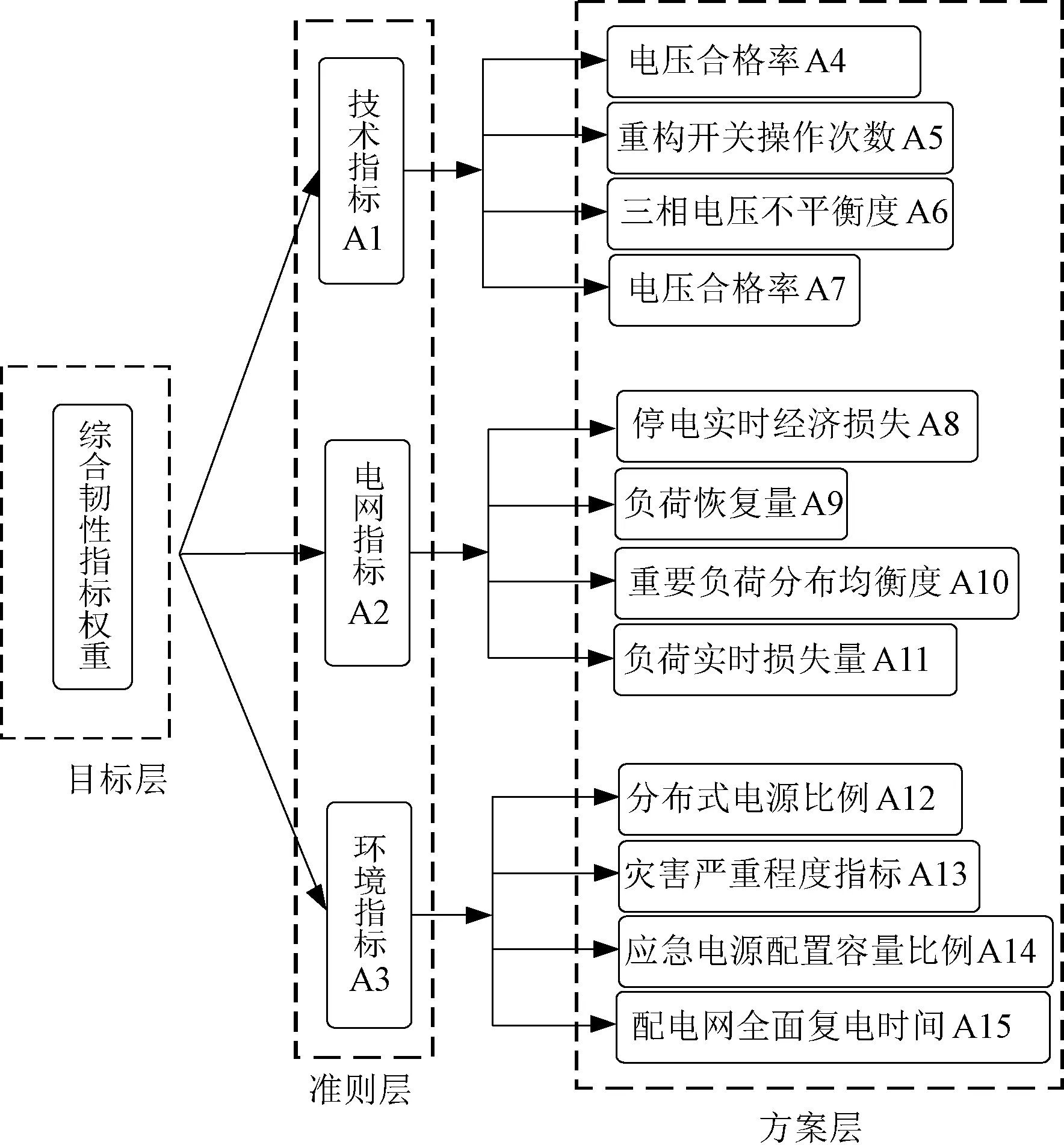
图3 模糊层次分析法示意图

由于传统AHP在维数较大时判断矩阵一致性非常繁琐，且一致性标准缺乏科学依据，也无法反映成对比较结果的不确定性，因此本文采用更有科学性和适用性的模糊AHP评价矩阵。模糊层次分析法的首要任务是确定同一层次中每对因素的相对重要性，利用三角模糊数，通过两两成对比较，构造模糊评价矩阵X=(xij)ζ×ξ。评价矩阵需满足如下性质：

(15)

xij=(lij,mij,uij)

(16)

其中

式中，mij为三角模糊判断最有可能值；lij和uij分别为下限值和上限值，表示模糊程度和比较尺度，uij-lij越大，模糊程度越大；uij和lij的值偏大，代表元素i相较元素j强烈偏极端重要，反之则元素i相较元素j强烈偏较强重要[20]。而后通过基于对数模糊偏好规划的模糊层次分析法排序，将模糊成对比较矩阵的优先级表示为对数非线性规划，并从模糊成对比较矩阵中导出清晰的权重[21]。

4.2 层次单排序及一致性检验

由于X的最大特征根λij是否连续依赖于xij，且受检验层的子目标数越多，X的不一致性越严重，引起的判断误差越大。理论上如果X是完全一致的判断矩阵，其绝对值最大的特征值应等于该矩阵维数，且xijxjk=xik,1≤i,j,k≤n。但在工程实际中所构造的对比矩阵难以同时满足上述众多等式，因而本文对一致性的要求为X绝对值最大的特征值和该矩阵维数相差不大，得到一致性指标CI为：

(17)

式中，m为受检验层次的子目标数；λmax为X的最大特征根。

为衡量CI大小，引入平均随机一致性指标RI：

(18)

式中，CI1,CI2,…,CI500为随机构造500个判断矩阵得到的一致性指标。而后可得一致性比例：

(19)

当CR<0.1时，认为判断矩阵的一致性是可以接受的，否则应对判断矩阵作适当修正[20]。

4.3 韧性指标模糊隶属度评分

对各指标而言，传统的二维评价(“好”与“坏”)过于简化，难以准确量化配电网韧性水平。因此本文采用模糊隶属度函数确定评估体系中单项指标评分。若梯形模糊数可表示为A=[a1,a2,a3,a4；1]，三角形模糊数可表示为B=[b1,b2,b3；1]，则梯形模糊数隶属度函数为[22]：

(20)

三角形模糊数隶属度函数可表示为[20]：

(21)

将专家打分的评分区间分为五个等级，分别为：非常好、比较好、一般、比较差、非常差，各等级对应分数见表1。隶属度函数如图4所示。

表1 等级分数区间

图4 隶属度函数示意图

结合4.1节模糊层次分析法得到的加权因子矩阵，可以得到最终的模糊评价结果矩阵E为：

E=Wλ

(22)

式中，W为归一化子指标加权因子矩阵；λ为隶属度关系矩阵。

5 算例分析

本节在Matlab R2016a平台上，选择重庆市渝北石船供电所10 kV小竹线配电网某次洪涝灾害前后电网数据作为算例对所提出的评估体系进行验证。该农区配电网靠近两江中心，含两江大道施工变箱、石船场镇、渝石中学、重桥村、小湾站、石船铸造厂等配电线路，易受洪涝灾害影响导致大面积停电事故，需要通过韧性评估找到现阶段规划运行中存在的问题。经过电网、市政多名专家对各项指标重要程度的讨论与分析，可得到表2～表5所示的指标成对比较矩阵(A1～A15分别对应层次分析法中各个指标，参见图3)。相较传统层次分析法单一比较矩阵而言，本文所使用的模糊层次分析法比较矩阵更能体现多名专家模糊判断的本质和决策思维的不确定性，更加科学、合理。

表2 准则层成对比较矩阵

表3 技术方案层成对比较矩阵

表4 电网方案层成对比较矩阵

表5 环境方案层成对比较矩阵

进而通过Matlab仿真可得指标权重值见表6。

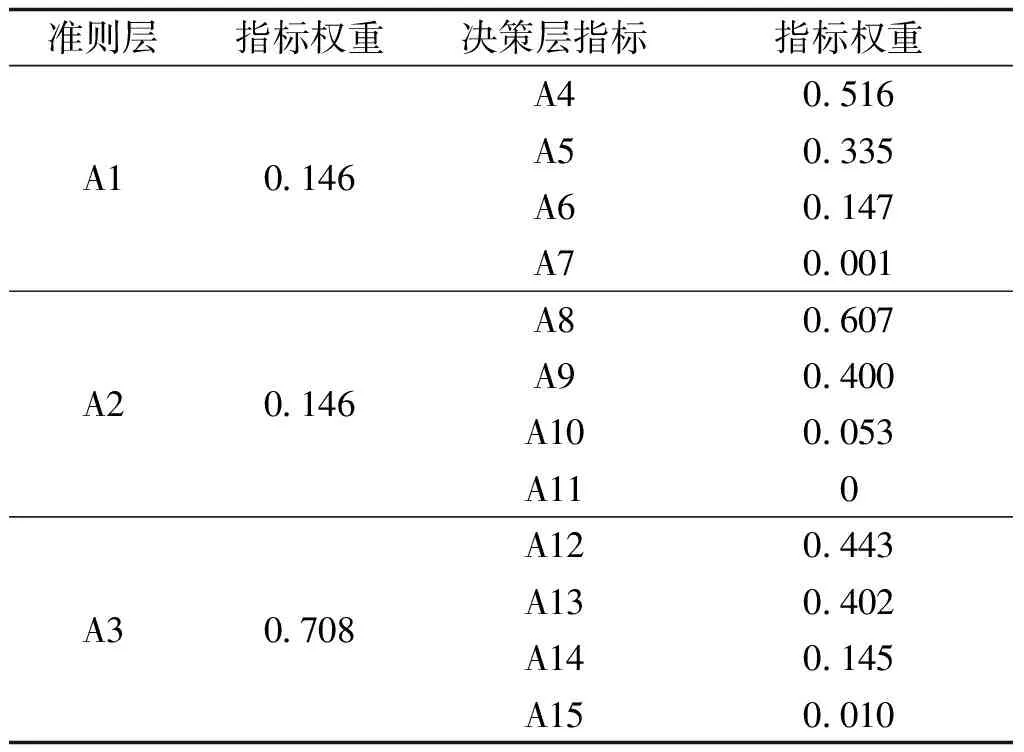
表6 指标权重值

由表6可以看出，决策层指标权重为：

(23)

式中，W1,W2,W3分别为包含电网、技术、环境架构下三项子指标的权重向量。

准则层指标权重W′为：

W′=(0.146,0.146,0.708)

(24)

对成对比较矩阵进行一致性校验：

(25)

可见专家提出的成对比较矩阵能够通过一致性校验。

本文采集重庆市渝北某农区辖区内配电网2020年某次洪涝灾害前后电网数据，按照第3节中提出的灾前、灾中、灾后指标计算方法，得到各决策层指标数值和通过隶属度函数计算的模糊指标评价结果见表7。

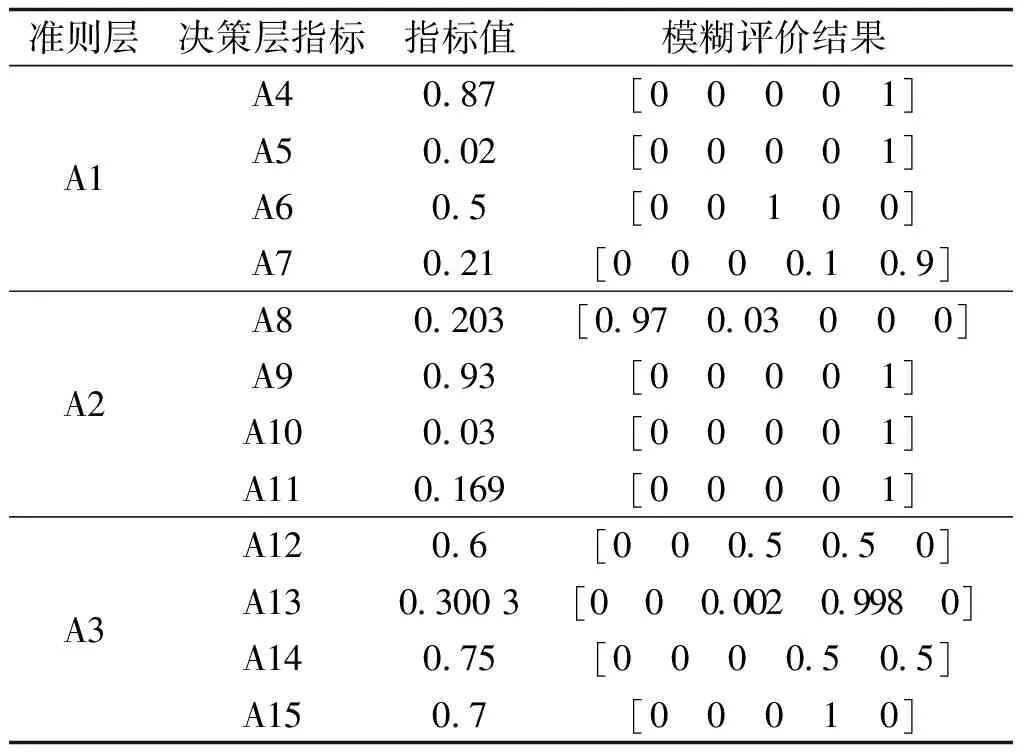
表7 指标值及模糊评价结果

由表7可以看出，韧性指标模糊隶属度评分矩阵为：

(26)

(27)

(28)

式中，λ1，λ2，λ3分别为包含电网、技术、环境架构下四项子指标的模糊评价隶属度矩阵。矩阵每行都是模糊评价结果，对于确定指标数据，模糊评价结果不是一个确定值，而是隶属于两个或多个评分区间。例如分布式电源比例(A12)评价结果为[0 0 0.5 0.5 0]，表示该结果50%隶属于“一般”，50%隶属于“比较好”，进而每行数据都可以被计算为来自不同专家的多次评估或不同时间收集的监测数据的平均结果。通过分析隶属度矩阵可知，得分最差的指标为重要负荷分布均衡度(A8)，说明渝北某农区负荷分布并不均衡，发生洪涝灾害很可能导致重要负荷供电需求无法被满足。但由于重要负荷可通过分布式电源(如微型燃气轮机)、电力弹簧、储能等元件实现恢复供电，因而该指标权重不高，不会对配电网韧性评分有太大影响。

除此之外，结合表6、表7可以分析得到，重构开关操作次数指标(A6)权重占比较大，但评分较差。这是由于在一定范围内增加开关切换次数可以优化重构方案、降低网络损耗，但一味切换开关可能导致人工费、设备损耗以及断电损失高于降低网损的收益，即现阶段渝北某农区重构开关操作次数存在冗余情况。灾害严重程度(A13)及分布式电源比例(A12)两项指标评分也处在“比较好～一般”区间，说明渝北某农区经受洪涝灾害影响后设备故障率和分布式电源配置还有进一步优化的空间。

由4.3节可知，决策层最终模糊评价矩阵为：

(29)

准则层最终模糊评价矩阵为：

(30)

根据表1，可以生成等级分数尺度向量(本文取等级分数区间中间值)为：

M=[1 3.5 5.5 7.5 9.5]

(31)

由此可得配电网综合韧性评价结果为：

R=E′MT=7.040

(32)

该结果属于评价区间“比较好”，经算例分析可知配电台区可通过优化重构开关操作次数和安装分布式应急电源提高韧性指标评分，进而提高防御、适应洪涝灾害和快速恢复供电能力。

6 结论

本文提出了一种包含状态、时间、架构三维度的实用型配电网韧性评估指标体系，体系中涵盖包括灾害严重程度在内的12项针对洪涝灾害下配电网的指标数学模型，可实现洪涝灾害下对配电网安全性、可靠性、灵活性、经济性、适应性进行综合、全面评估。通过模糊层次分析法计算指标权重矩阵，体现指标数据间内在联系的同时反映对比关系模糊程度。同时通过模糊隶属度函数评价各指标数值隶属的等级区间，辨识配电网规划调度的薄弱环节，进而得到配电网综合韧性评价结果。通过在实际配电网中的应用分析可以看出，本文所提出的评估指标体系能有效反映洪涝灾害下配电网重要负荷分布均衡度、分布式电源配置、重构开关操作等方面的缺陷，为提高配电网预防、应对、适应自然灾害提供理论支持。