一种适应新型电力系统的加速型工程最速比例-积分控制器

李军，黄卫剑，陈锦攀，谢洪途，王朋，朱亚清，潘凤萍，李德波

(1. 广东电网有限责任公司电力科学研究院，广东 广州 510080；2. 南方电网电力科技股份有限公司，广东 广州 510080；3. 中山大学 电子与通信工程学院，广东 广州 510275；4.南方电网数字电网研究院有限公司，广东 广州 510623)

基础工业如电力工业[1]等历来是各种控制技术应用的重地，基础工业是关系国计民生和国家战略的基础支柱产业，其发展水平直接决定了一个国家的技术水平和经济发展水平。工业控制技术(如基础工业过程控技术)代表了基本的工业生产工具，直接决定了工业生产力水平。

1788年，瓦特借助离心调速器[2]实现了蒸汽机转速控制，对18世纪以蒸汽机为代表的第一次工业革命起到了巨大的推动作用。离心调速器实现了一种比例作用的反馈控制即瓦特原理[3]，代表了第一代基础工业过程控制技术[4]，离心调速器明显的问题是存在系统稳态误差[5]。

从19世纪末到20世纪上半叶，电机工程[6]的发展开启了第二次工业革命，对控制提出了较高的要求。1936年考仑德(A. Callender)和斯蒂文森(A. Stevenson)发明出比例-积分-微分(proportional-integral-derivative，PID)控制器[7-13]，代表了第二代基础工业过程控制技术[4]。PID控制的结构简单、鲁棒性能[14]良好，适用于大多数的工业过程控制[15]，在包括火电机组[16]在内的工业过程控制领域得到广泛应用，推动形成了巨大的工业生产力。

PID在工业控制工程应用上是成熟的，在理论提炼上是完善的，PID理论的完善对整个控制科学的推动作用极其巨大，多年来并没有出现第二个像PID这样的控制。但是这并不代表PID控制已经能够很好地满足工业过程控制的需求，研究人员认为PID控制存在动态控制精度不高的问题。长期以来，围绕着改进或提高PID控制性能的各种研究一直没有间断，如非线性PID控制[7]、自适应PID控制[8]、基于非线性滤波的PID控制[9]、最优PID控制[10]、基于输出补偿的PID控制[11]、基于高效滤波的PID控制[12]、自耦PID控制[13]等。2002年, 陈翰馥[17]指出：“我国的传统工业要改造，大量使用的PID控制器，需要用精度高、适用性更强的控制器来取代”，但是20多年过去了，取代PID控制器的愿望并没有实现。钱积新[18]指出：“实际上，在工业过程中面对复杂多变的生产过程，对控制系统的各种要求除了PID算法尚被基本认可外，其他的算法都很难长期、有效地得到应用”。

从观测角度来看，PID中的P作用(proportional)、I作用(integral)、D作用(derivative)代表了反馈控制中的3个基本观测机制，具体来说是P作用的当前观测机制、I作用的常值观测[4]机制、D作用的超前观测机制。从构造I作用、D作用的方法看，二者(常规微分器)基于一阶惯性滤波器(first order inertial filter，FOIF)[19]构造，FOIF属于一种典型的指数型跟踪律，因此二者代表的是指数型常值观测机制、指数型超前观测机制，PID控制代表了一种指数型控制机制。

在工业过程控制领域，不可能一直停留在PID控制，需要产生出能够超越现有PID控制的新型基础控制技术(new foundation control technology，NFCT)，但是实现超越PID控制的NFCT的过程漫长且艰难。在控制科学发展过程中，随着一些本质问题的揭示，必然能够实现超越PID控制的NFCT。

国家的重大需求是原始创新的根本动力，随着我国碳达峰、碳中和能源目标的提出，以风力发电、太阳能光伏发电为代表的新型绿色能源得到迅猛发展，电网亟需快速增加深度调峰、快速调频能力，这是新型电力系统的基本特点和标志。在新型电力系统背景下，以燃煤火力发电为代表的传统电力工业形势严峻，从现有火电机组重要过程控制回路实现深度调峰快速调频性能的角度，PID控制难以再适应，由此催生出满足此种需要的NFCT。

2018年，文献[19] 揭示PID控制的一种本质缺陷：常规积分(conventional integrator，CI)作用跟踪常值扰动效率不高。通俗地理解是：在控制理论的研究中存在一个看不见的问题，即长期以来对控制结构的研究并没有改变指数型控制机制，这就解释了为何多年来并没有出现第二个像PID这样的控制。2018年，广东电网有限责任公司的科研团队发明出一种基于工程最速跟踪滤波器(engineering fastest tracking filter，EFTF)[4]的工程最速控制器(engineering fastest controller，EFC)[4], EFC是工程最速比例-积分(engineering fastest proportional- integral，EFPI)控制器与工程最速超前观测器(engineering fastest leading observer，EFLO)的串级结构，EFC代表了一种显著区别于PID控制的NFCT，即第三代基础工业过程控制技术[4]，显著提高了反馈控制性能，彻底摆脱了模型束缚，适应目前新型绿色能源快速发展的客观需要。文献[4]指出：“以EFC为核心开发出的火电机组辅助调频外挂控制系统，在广东省主力火电机组得到快速普及，仅在2020年1月—2021年6月期间,就已经应用于38台火电机组(总计容量为25 600 MW)的辅助调频外挂控制系统商业合同项目”。

文献[4]给出了EFC与最优PI(optimal proportional-integral，OPI)、最优PID(optimal PID，OPIP)在难控制过程控制性能的对比结果，结果显示，相对OPI、OPID，EFC显著提高了调节性能，其中EFC的外扰抑制性能分别提高了78.6%、43.7%。但是在火电机组的许多控制回路中，采用了比例-积分(proportional-integral，PI)控制，主要原因是PI参数整定相对简单。同理，为了满足火电机组多种控制回路的需求，需要单独运用EFPI控制器，但是在实践中发现EFPI的性能相对不足够。从发展EFC的角度来看，需要针对EFPI存在的问题进行改进。研究人员在EFTF的基础上发明出了一种加速型工程最速跟踪滤波器(acceleration engineering fastest tracking filter，AEFTF)，采用AEFTF构造出一种加速型工程最速比例-积分(acceleration engineering fastest proportional-integral，AEFPI)控制器，较好解决了EFPI存在的问题，目前AEFPI已经进入到商业应用。AEFPI是EFC的继续深入发展，二者代表了一种已经进入到大规模商业应用的工业过程控制技术。

从控制学界的角度，能够运用于工业过程控制的控制技术可能远不止PID控制，例如模型预测控制(model predictive control, MPC)[20]、动态矩阵控制(dynamic matrix control, DMC)[21]、广义预测控制(generalized predictive control, GPC)[22]、状态反馈控制(state feedback control, SFC)控制[23]、Smith预估控制[24]、内模控制(internal model controller, IMC)[25]、自适应鲁棒控制[26]、H∞鲁棒控制[27]、滑模控制[28]等，应该说，这些控制技术在许多领域获得了成功应用，黄德先等[29]指出:“模型预测控制可以说是目前现代控制理论在过程控制中应用最成功的控制方法”。

需要指出的是, “成功应用”与“商业应用”是2个概念：“成功应用”仅是表明一种控制技术已经能够进入工程应用；“商业应用”则表明一种控制技术已经成熟，已经能够为应用企业带来商业利润了，例如PID控制代表的是一种成熟的基础性工业过程控制技术。研究人员认为，取得“成功应用”的控制技术有很多种，但是从推动工业生产力的角度来说，大量PID控制之外的控制技术并没有推动形成大规模的工业生产力或者进入到大规模的商业应用。一种控制技术能否进入到商业应用是由多种综合因素决定的。

EFC反映出在工业过程控制实际中，已经完成了从指数型控制机制到工程最速型控制机制的过渡，AEFPI是工程最速型控制机制的最新发展。

本文中函数、参数、变量的表达具有唯一性，可相互引用。出于表述简洁性的需要，如文中无特别说明，时间、时间常数单位为s，加速度单位为s-2，比例、增益、阶次的量纲为一。

1 加速型最速跟踪滤波器

2021年，李军[30]发明出一种加速型最速跟踪滤波器(acceleration fastest tracking filter，AFTF)，具有恒定的输出加速度。

AFTF的传递函数

(1)

式中：TT为AFTF的跟踪时间常数；s为拉普拉斯算子。

输入单位阶跃，AFTF输出为：

(2)

式中：PAFTF(t)为AFTF在阶跃输入的过程输出；aPV为AFTF输出的加速度。

令TT=100 s，得到AFTF单位阶跃输入的过程输出，如图1所示。

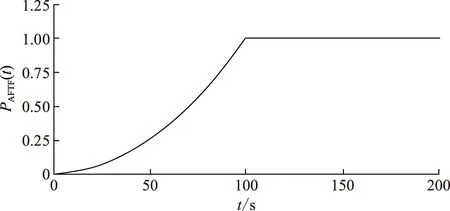
图1 AFTF的过程输出特性示意图Fig.1 The diagram of process output characteristic of AFTF

在数字控制系统〔如分散控制系统(distributed control system，DCS)[31]〕实现AFTF主要存在输入与输出的稳态误差问题，即对一个过程进行AFTF滤波，在过程进入稳态后，AFTF的输出与输入存在稳态误差。数字控制系统存在数字量化误差，AFTF由纯滞后环节构造，纯滞后环节的输入为实时数据，纯滞后环节的输出为历史数据。在DCS中，出于减小内存的需要，实时数据与历史数据的数字量化误差不相同，因此存在实时数据与历史数据的稳态误差，采用AFTF构造的加速型最速积分器(acceleration fastest integrator，AFI)存在稳态误差的累积问题。

2 加速型工程最速跟踪滤波器

针对AFTF的输出与输入的稳态误差问题，需要对AFTF进行工程化改造，所谓FTF工程化改造，即近似FTF的工程方法。

首先采用串级纯滞后环节近似AFTF，得到近似AFTF(approximations AFTF，AAFTF)，即

(3)

式中：fAAFTF(s)为AAFTF的传递函数；n为纯滞后环节串联阶数。n越大，AAFTF与AFTF的近似度越高，其中在n=16、TT=100 s时，得到AAFTF单位阶跃输入的过程输出PAAFTF(t)，如图2所示。

图2 AAFTF的过程输出特性示意图Fig.2 The diagram of process output characteristic of AAFTF

工程上经常用FOIF近似纯滞后环节[32]，采用FOIF替换AAFTF中纯滞后环节，得到加速型工程最速跟踪滤波器(acceleration engineering fastest tracking filter，AEFTF)的传递函数

(4)

其中在n=16、TT=100 s时，得到AEFTF在单位阶跃输入的过程输出PAEFTF(t)，如图3所示。

图3 AEFTF的过程输出特性示意图Fig.3 The diagram of process output characteristic of AEFTF

n越大，AEFTF与AFTF的近似度越高，在工程上，取n=16已经足够了。本文中如无特别说明，默认n=16。

3 加速型工程最速积分器

AEFTF是构造加速型工程最速积分器(acceleration engineering fastest integrator，AEFI)的基础，在了解AEFI之前，首先需要了解构造CI的方法，采用FOIF构造CI，如图4所示。

图4 CI示意图Fig.4 The diagram of CI

CI表达式为

(5)

式中fCI(s)、TFOIF、TI分别为CI的传递函数、FOIF惯性时间常数、CI积分时间常数，TI=TFOIF。

同理，采用AEFTF构造AEFI，如图5所示。

图5 AEFI示意图Fig.5 The diagram of AEFI

在数字控制系统中，AEFTF的输入与输出为实时数据，不存在稳态误差的问题，因此采用AEFTF构造AEFI，解决了累积误差的问题。

AEFI表达为

(6)

式中：fAEFI(s)为AEFI的传递函数；TAEFI为AEFI的时间常数。

当n=16、s趋于∞或s趋于0时，fAEFI(s)分别简化为：

(7)

根据式(7)，令TAEFI=TI，将AEFI与CI进行对比：当s趋于∞，AEFI的增益是CI的0.117 6倍；当s趋于0，则AEFI的增益是CI的1.454 5倍。这是AEFI积分作用效率显著高于CI的数学依据，积分作用效率代表了一种对常值观测的性能。

令TI=TAEFI=100 s、n=16，输入单位阶跃，得到的AEFI的过程输出PAEFI(t)、CI的过程输出PCI(t)，如图6所示。很显然，AEFI的积分作用效率显著高于CI。

图6 AEFI、CI单位阶跃输出特性Fig.6 The diagram of unit step output characteristic of AEFI and CI

4 加速型工程最速比例-积分控制器与参数整定

EFPI基于EFTF构造，在EFPI基础上，用AEFTF替换EFTF，得到AEFPI。

EFPI表达为：

(8)

式中：fEFPI(s)、KEFPI分别为EFPI的传递函数、串级比例增益；fEFI(s)、TEFI分别为工程最速积分器(engineering fastest integrator， EFI)的传递函数、积分时间常数；fEFTF(s)、TEFTF分别为EFTF的传递函数、时间常数。

AEFPI结构如图7所示。

图7 AEFPI示意图Fig.7 The diagram of AEFPI

AEFPI的传递函数

fAEFPI(s)=KAEFPI(1+fAEFI(s)).

(9)

式中KAEFPI为串级比例控制增益。

AEFPI参数整定是一个重要的问题，建立过程的模型(建模)有利于AEFPI参数整定。从工程的角度，建模不是为了获取过程的准确模型，而是为了方便控制器参数整定，并且能够避开复杂繁琐的数学解析的中间过程。AEFPI参数整定基于一种ZM模型(Ziegler-Nichols model，ZNM)[4]，ZNM代表了一种直观的工程模型。

ZNM的传递函数

(10)

式中KZN、τZN、TZN分别为增益、纯滞后时间常数、时间常数。

对于有自平衡能力的过程，AEFPI、EFPI参数与ZNM的关系为：

(11)

式(11)给出的AEFPI参数整定方法完全避开了复杂繁琐的数学解析中间过程，但是依据式(11)得到的AEFPI参数并不代表AEFPI的性能已经最高，在控制实际中，对AEFPI参数进行适当调整也是可能的。

AEFI的手动跟踪是一个重要问题，在手动状态下，AEFI输出跟踪手动状态的当前输出减去AEFI的当前输入。

5 仿真实验

仿真控制系统为图8所示。

图8 控制系统示意图Fig.8 The diagram of control system

图8中，BBP为黑箱过程(black box process，BBP)，EDCM为外扰耦合模型(external disturbance coupling model)，RF为斜坡函数(ramp function)，控制器可为AEFPI、EFPI、PI等。BBP为典型的难控过程。

出于对比需要，继续沿用文献[4]给出的BBP、EDCM、RF、OPI参数。其中RF速率为10-3s-1，RF长度为1 800 s。

文献[4]给出的BBP、EDCM为：

(12)

式中fBBP(s)、fEDCM(s)分别为BBP、EDCM的传递函数。

PI的传递函数

(13)

式中KP为PI的比例增益。

文献[4]给出的OPI参数为：KP=0.69、TI=366 s。所谓OPI参数，即在一定的相位稳定裕度的条件下，求取PI最小的TI值，代表对常值的观测性能最高。求取OPI参数存在复杂繁琐的数学解析中间过程。

根据给出的BBP参数，建立BBP的ZNM，如图9所示，图9中PBBP(t)、PZNM(t)分别为BBP、ZNM在单位阶跃输入的过程输出。

根据图9，得到KZN=1、τZN=226 s、TZN=276 s，进一步得到

图9 ZNM过程输出特性Fig.9 The diagram of process output characteristic of ZNM

(14)

依据式(11)，得到EFPI参数为KEFPI=1、TEFI=502 s，得到A组AEFPI参数为KAEFPI=1、TAEFI=502 s。出于对比需要，设置B组AEFPI参数为KAEFPI=1.25，TAEFI=502 s。

令过程给定为1、外扰为0，得到EFPI、AEFPI、OPI的仿真实验结果，如图10所示，图中POPI(t)、PEFPI(t)、PAEFPI(t)分别为OPI控制BBP、EFPI控制BBP、AEFPI控制BBP的过程输出。

图10 AEFPI、EFPI、OPI控制特性对比结果Fig.10 The diagram of contrast results of AEFPI and EFPI、OPI control characteristics

根据图10，得到AEFPI、EFPI、OPI控制的主要性能指标，见表1。

表1 AEFPI、EFPI、OPI控制的主要性能指标Tab.1 Main performance Index of control of AEFPI and EFPI and OPI

调节时间是指过程进入到小于5%偏差的时间，相对于OPI，AEFPI显著提高了调节性能，EFPI的调节性能相对不高。

令过程给定为0、外扰为RF，得到AEFPI、EFPI、OPI的仿真实验结果，如图11所示。

根据图11，得到AEFPI、EFPI、OPI控制的外扰抑制主要性能指标，见表2。

图11 AEFPI、EFPI、OPI外扰抑制特性对比结果Fig.11 The diagram of contrast results of AEFPI and EFPI and OPI disturbance rejection characteristic

表2 AEFPI、EFPI、OPI外扰抑制的主要性能指标Tab.2 Main performance Index of disturbance rejection of AEFPI and EFPI and OPI

用抑制RF最大偏差衡量AEFPI、EFPI、OPI的外扰抑制性能，相对OPI，AEFPI(A组参数)的外扰抑制性能提高了10.1%, AEFPI(B组参数)的外扰抑制性能提高了23.5%，EFPI的外扰抑制性能提高了14.6%。在火电机组过程控制，能够将外扰抑制性能提高10%，已经是效果明显。

综合来看，相对AEFPI，EFPI的调节性能、外扰抑制性能不高。

6 工程应用

2022年2月期间，将EFC应用于某电厂2号1 000 MW超临界火电机组的二级过热蒸汽温度控制回路，并且与PI控制进行对比，其中A侧二级过热蒸汽温度控制系统采用AEFPI控制，B侧二级过热蒸汽温度控制系统采用PI控制，得到的对比结果如图12所示。

图12 AEFPI与PI控制特性的对比结果Fig.12 The diagram of contrast results of AEFPI and PI control characteristics

由图12可知，在给出过程趋势变化范围，A侧二级过热蒸汽温度波动范围为593～603 ℃，B侧二级过热蒸汽温度波动范围为589～606 ℃，很明显，相对PI控制，采用AEFPI控制显著提高了所述二级过热蒸汽温度控制系统的控制性能。

7 推动工程最速控制器发展的载体

一个控制技术能否得到发展的关键是看它是否有具体的载体。在新型绿色能源的快速发展的背后是新能源革命，文献[4]指出：“在我国发电侧结构中，目前火电机组在电网总装机容量中占比达到 52% ，通过对现有火电机组控制系统优化(即大幅提升深度调峰和快速调频性能)来增加电网调峰、调频容量,是一种投资省、见效快的方式，是目前阶段电网快速增加调峰、调频能力的主要方式”。推动新能源革命的快速发展就是EFC、AEFPI等发展的具体载体，以EFC为核心开发出的火电机组辅助调频外挂控制系统，目前已经在广东省主力火电机组基本普及，极大地推动了广东省电力系统新能源革命的发展进程。

EFTF是构造EFC的核心基础，AEFTF是EFTF的继续发展。AEFPI于2021年10月后开始投入商业应用，其代表了一种基本的加速型工程最速控制器(acceleration EFC，AEFC)，是EFC的继续发展。

8 结束语

AEFTF、AEFPI及EFTF、EFPI、EFLO、EFC等均为工程实践的产物，是控制机制上的原始创新，是对控制科学的重要发展。

为实现碳达峰、碳中和的能源目标，新型绿色能源在电网中占比越来越大，要求电网具有越来越大的调峰、调频能力。提高现有火电机组深度调峰、快速调频能力将是未来若干年内新型电力系统发展的一个重要方向。采用AEFPI、EFC等是快速提高现有火电机组的深度调峰、快速调频能力的最直接有效方法。

以EFC、AEFPI等为核心的火电机组辅助调频外挂控制系统的商业应用项目已经证明，EFC、AEFPI等是一种成熟的工业控制技术，适应了新能源革命快速发展的需要，有效地解决了新型绿色能源大规模接入电网的调节、安全稳定等重大关键问题，对未来实现碳达峰、碳中和的能源目标具有积极意义。