基于低分辨率红外光谱分析的燃烧气相组分温度测量
李兆宇,张仲侬,郜宁,曲欣,娄春
(1. 新疆新能集团有限责任公司乌鲁木齐电力建设调试所,新疆 乌鲁木齐 830000;2. 国网新疆电力有限公司电力科学研究院,新疆 乌鲁木齐 830000;3. 华中科技大学煤燃烧国家重点实验室,湖北 武汉 430074)
温度是燃烧火焰的重要参数,燃烧过程中的化学反应速率与温度有关,燃烧生成的氮氧化物也与温度密切相关,对燃烧温度的测量一直是燃烧研究的重点[1-2]。煤等固体燃料燃烧会产生焦炭、飞灰等固体颗粒以及CO2、H2O等气体;天然气、石油等含碳气液燃料燃烧过程中,除了生成碳烟颗粒物之外,主要产生CO2、H2O等高温气体[3]。已有研究表明,由于化学反应和热量传递的瞬时性,燃烧火焰中固体颗粒温度和气体温度存在明显不同,需要对两者温度都进行准确测量[4-5]。此外,对于非含碳气液燃料(如H2、NH3等),其燃烧时只产生H2O等高温气体,更需要测量气体温度[6]。燃烧温度的常用测量方法有热电偶法、声学法和光学法。光学法作为一种非接触式的测温方法,对被测对象无干扰且响应速度快,具有较好的发展前景,按照有无外加光源,光学法可分为主动式和被动式。被动式方法通过分析燃烧火焰自发辐射来获得温度结果,由于不需要外加光源而只需布置接收装置,具有系统紧凑、易于实施等特点[7]。自发辐射燃烧诊断技术在燃烧火焰温度和组分含量测量中也有较多应用,主要包括多波长测温技术和热辐射成像技术。Reynolds[8]提出了基于自发射光谱分析的多波长高温计的概念和理论,蔡小舒等[9]、戴景民[10]、程晓舫等[11]、符泰然等[12]在多波长测温方法发展及应用方面均开展了相关研究工作。周怀春等[13]将热辐射图像处理与辐射传递方程求解相结合,提出了热辐射成像技术,并将该技术应用于大型电站燃煤锅炉的燃烧温度监测;刘冬等[14]、许传龙等[15]也开展了基于热辐射成像的燃烧温度场测量研究。但上述研究均基于检测固体颗粒在可见光波段的辐射信息进行测温,测得的温度为燃烧火焰中固体颗粒物温度。
火焰光谱学的研究表明[16],燃烧产生的气体产物(CO2、H2O等)主要在红外波段辐射能量且具有强烈的光谱选择性,需要利用红外波段探测器,通过光谱分析技术进行温度测量。傅里叶变换红外光谱(Fourier transform infrared spectroscopy,FTIR)技术被广泛用于红外光谱发射测量,南京理工大学王俊德等[17]、李燕[18]等根据FTIR遥测收集的固体推进剂燃烧发射的红外光谱信号,通过分子发射基谱线强度计算热气体温度及气体产物含量;中国科学研究院刘志明等[19]基于高分辨率传输分子吸收数据库(high-resolution transmission molecular absorption database,HITRAN),提出高温参考谱模型法,根据FTIR测得的红外光谱计算热气体的温度,高乾坤等[20]则将该方法用于高温窑炉内气体温度及CO气体体积分数;杨百翰大学Ellis等[21]提出采用FTIR获取H2O在1.69~2.15 μm波段的发射光谱,并根据其中2个特定波段的强度比值计算天然气燃烧火焰中气体温度;Cięszczyk[22]则利用CO2在4.3 μm波段附近不同光谱发射信息的比值来获得辐射传递路径上平均气体体积分数和气体温度。由上述研究可知,基于气体红外发射光谱测量气体温度,主要是依据特定波段的绝对光谱强度值、光谱强度比值或谱带积分强度比值。然而,谱线线强大小及其比值容易受测量噪声的影响而导致测温精度降低,有必要发展宽谱带范围内基于气体红外辐射强度分布的温度测量方法。此外,上述研究均利用FTIR来获取高光谱分辨率的气体红外辐射强度分布,但FTIR仪器成本较高,对使用环境的要求也较高,在工业应用中难以大规模推广。
近年来,随着半导体技术的发展,基于InGaAs、PbS的低分辨率红外发射光谱仪因成本低、对使用环境要求不高而得到较多应用[23]。本文采用低分辨率红外发射光谱仪检测燃烧火焰中气体发出的红外辐射光谱,再通过气体辐射特性模型及粒子群优化(particle swarm optimization,PSO)算法,根据宽谱带气体红外发射光谱强度同时计算气体温度及组分体积分数。最后,将该方法用于实验室乙烯扩散火焰的气体温度测量,以验证其有效性。
1 测量方法及原理
1.1 气体介质光谱辐射强度计算
气体的辐射光谱具有强烈的非灰特性,由大量的谱线组成。这些谱线的线性主要受气体分子旋转、振动和碰撞过程影响。为描述谱线的线形,学者们提出了大量的模型,其中Lorentz线形应用最为广泛。根据Lorentz线形,气体的光谱辐射特性分布可以根据式(1)计算获得[24]:
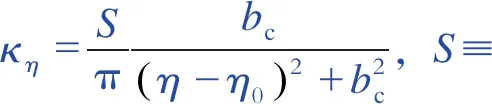
(1)
式中:κη为气体的光谱吸收系数,m-1;S为谱线强度,m-2;bc为在波数单位下的谱线半宽,m-1;η为波数,m-1;η0为谱线中心的波数,m-1;Δη为气体辐射波段。
气体的谱线半宽
(2)
式中:c0为真空中的光速,c0=3×108m/s;D为气体分子直径,m;m为气体分子的质量,g;p为气体压力,Pa;T为气体温度,K;k为玻尔兹曼常数,k=1.307×10-23J/K;下标“0”代表标准状态的参数值。式(1)、(2)中所需要的气体辐射参数(谱线半宽等)的高分辨率光谱分布可在数据库HTEMP2010中获得。
由式(1)可得不同温度及体积分数下高分辨率气体辐射光谱特性分布。假设所测量的气体层温度和体积分数均匀分布并考虑其内部的自吸收作用,气体层发射的光谱辐射强度[24]
Iη=Ib,η(1-eκηL).
(3)
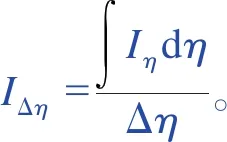
1.2 PSO算法
PSO算法是一种基于生物群体模拟的智能优化算法,该算法可通过移动区域内随机分布的粒子,迭代搜索得到目标函数的最优位置,即所考虑问题的最优解。在每次迭代过程中,粒子群中都存在2个最优粒子,分别为本次迭代中粒子群中的最优粒子和之前数次迭代过程中的最优粒子(即全局最优解)。在PSO算法中,主要利用上次迭代的极值来更新粒子的位置,展开下一次迭代。迭代的计算公式为[25-26]:
Vi(t+1)=Vi(t)+C1·R1·[Pi(t)-Xi(t)]+
C2·R2[Pg(t)-Xi(t)],
(4)
Xi(t+1)=Xi(t)+Vi(t+1).
(5)
式(4)、(5)中:C1、C2为加速系数,本文取C1=C2=2.0;R1、R2为区间[0,1]内均匀分布随机系数;Xi(t)、Vi(t)分别为第i个颗粒在第t次迭代的位置矢量、速度矢量,本文中每个颗粒的位置由气体温度T和体积分数Y组成,因此颗粒位置和颗粒速度可分别表示为Xi=(T,Y)T、Vi=(vT,vY)T,vT、vY分别为颗粒中温度分量和体积分数分量的速度;Pi(t)、Pg(t)分别为第t次迭代中第i个颗粒的最优位置和全局最优位置。
将采集到的光谱强度与理论强度对照,可得到气体温度和体积分数。每个粒子的适应度值
(6)
式中:N为光谱仪采集的光谱辐射强度数据个数;Ii,meas为测量得到的光谱辐射强度,W/(m3·sr);Ii为理论计算得到的光谱辐射强度,W/(m3·sr)。
PSO算法的计算流程为:
a)设定搜索温度和气体体积分数的搜索区域,初始化粒子群的位置,主要包括在搜索区域内随机产生颗粒的位置及颗粒的速度,并且设定全局最优解的精度要求和迭代次数的要求。
b)通过目标函数计算得到每个颗粒的适应度值。
c)将计算得到的适应度值与该颗粒自身的最优值比较,如果该适应度值低于该颗粒自身的最优值,则将该适应度值替换为该颗粒自身的最优值。
d)将第i个颗粒的适应度值与全局最优解比较,如果该适应度值低于全局最优解,则该适应度值替换为全局最优解。
e)根据式(4)和(5)更新粒子群的位置。
f)判定所得到的全局最优解及迭代次数是否达到步骤a)中设定的要求:若满足,则停止迭代,输出结果;若不满足,则跳转至步骤b)继续迭代。
1.3 实验装置
在燃烧火焰气体温度的实验测量中,本文搭建的实验平台主要由气体供应系统和光谱检测系统组成,气体供应系统由气体储蓄装置、流量控制器及气体管路组成,光谱检测系统由光学平移台、步进电动机、伴流扩散火焰燃烧器、光谱仪及数据处理装置组成。实验装置系统如图1所示。实验采用的光谱仪型号为AvaSpec-NIR256,测量波长范围为1 300~1 700 nm,该波段内有较为强烈H2O辐射谱线。
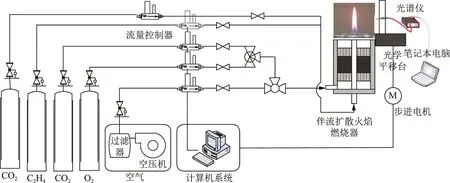
图1 实验装置系统Fig.1 Experimental device system
2 测量方法的数值验证
在实验测量之前,采用模拟反演计算的方式验证气体温度和体积分数测量结果的精确性。设定A组、B组工况,编号分别为A1—A10、B1—B10:A组工况中,H2O体积分数为20%,气体温度从2 000 K升高至2 900 K;B组工况中,气体温度为2 400 K,H2O体积分数从4%增加至40%。具体工况参数见表1。根据设定的工况,通过气体辐射计算得到1 300~1 700 nm波段的光谱辐射强度。同时,考虑实验过程光栅光谱仪的测量误差以及其分辨率较低,导致无法精确测量到气体光谱特征的问题,在计算得到的光谱辐射强度值基础上加入10%的噪声,经高斯平滑处理后,作为模拟反演计算中的测量数据。然后根据模拟得到的测量数据,采用PSO算法反演计算气体温度和H2O体积分数,并与设定值比较,结果如图2所示,其中YH2O为H2O体积分数。从图2可见,利用PSO算法反演计算得到的H2O体积分数误差小于5%,气体温度误差小于3%。这个结果说明PSO算法在计算气体温度及体积分数时具有较高的精度,并且可以较好地克服光谱采集分辨率低及测量数据存在误差等问题。
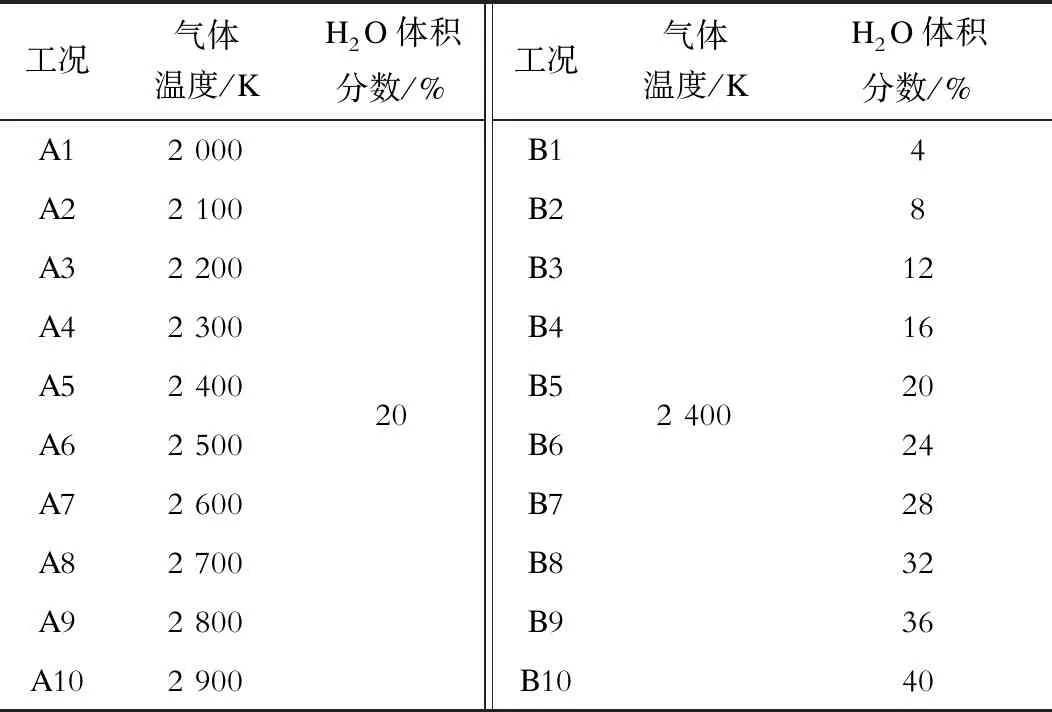
表1 反演工况参数Tab.1 Inversion case parameters
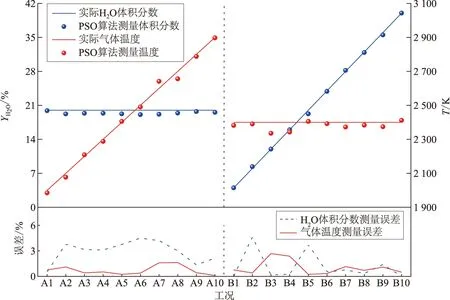
图2 气体温度及H2O体积分数的测量结果及相对误差Fig.2 Measurement results of gas temperature and volume fraction of H2O and the relative errors
将计算得到的气体温度和H2O体积分数代入气体辐射计算模型,得到1 300~1 700 nm红外光谱辐射强度的反算值(即理论光谱强度),将其与测量光谱强度进行比较,两者的吻合程度也可以验证算法的可靠性。图3给出了H2O体积分数为20%,温度为2 000 K、2 200 K、2 400 K、2 600 K、2 800 K时的理论观光谱强度和测量光谱强度的对比。从图3可以看出,在各气体温度下,理论光谱强度与测量光谱强度具有较好的一致性,验证了PSO算法用于气体温度及H2O体积分数反演计算的准确性和可靠性。
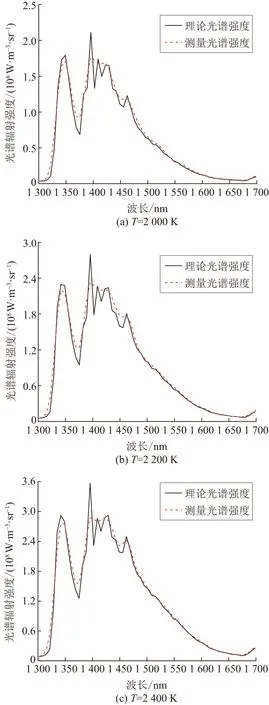
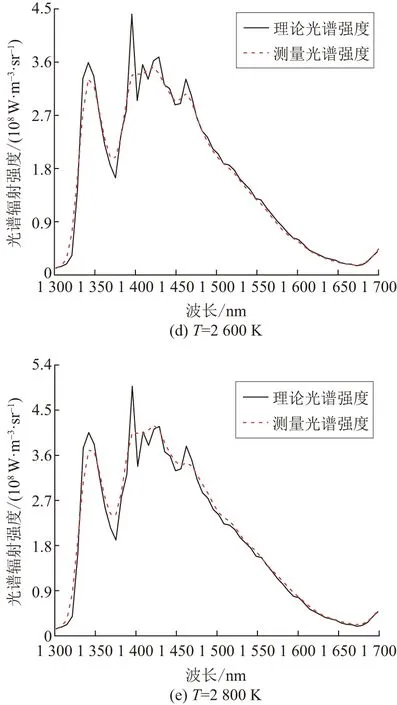
图3 不同设定温度时理论光谱辐射强度分布和测量结果对应的光谱辐射强度分布Fig.3 Theoretical spectral radiative intensity distribution and spectral radiative intensity distribution corresponding to the measurement results at different set temperatures
图4给出了H2O体积分数为20%,温度分别为2 000 K、2 200 K、2 400 K、2 600 K、2 800 K时PSO算法收敛情况,本文中所采用的最高迭代次数为5 000。从图4可见:随着计算不断迭代,计算得到的适应度值呈现不断减小的趋势,当迭代次数达到3 500时,其值逐渐趋于稳定;在整个迭代过程中,适应度值总体减小约60%。
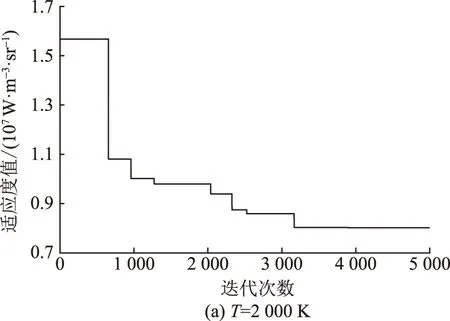
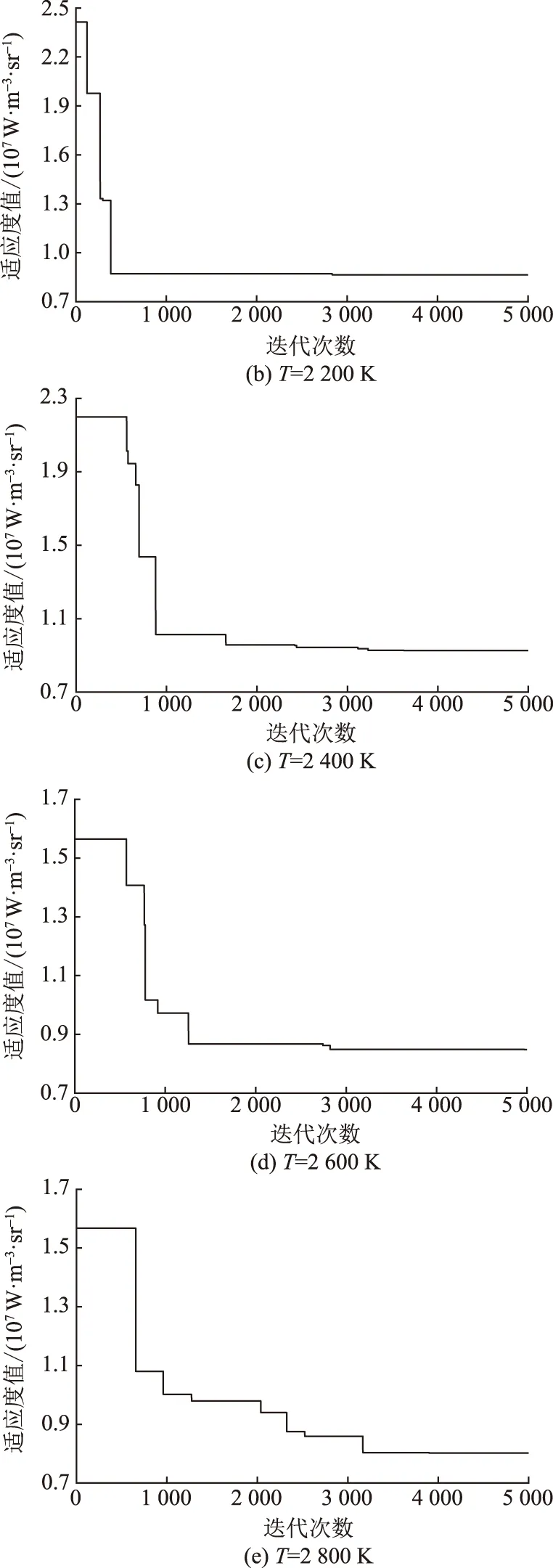
图4 不同设定温度时PSO算法收敛情况Fig.4 Convergence of PSO algorithm at different set temperatures
3 实验测量及结果
基于近红外光谱检测技术,开展富氧气氛下乙烯扩散火焰中气体温度以及H2O体积分数的测量实验,燃料侧为C2H4和CO2的混合气体,氧化剂为O2和CO2的混合气体。火焰工况见表2,其中:χO2为氧化剂中的氧气体积分数;Zst为化学计量混合分数,该参数对火焰结构有重要影响。
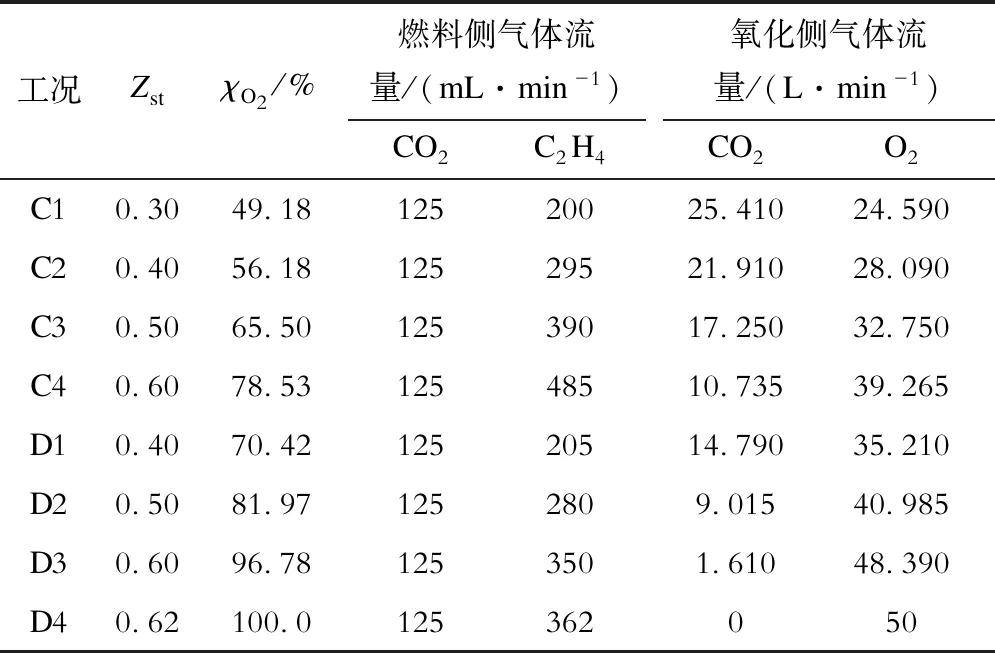
表2 工况参数Tab.2 Case parameters
实验测量得到的光谱辐射强度分布如图5所示。从图5可以看出,火焰内高温介质在1 300~1 700 nm波段内的辐射强度主要在1 350 nm、1 390 nm、1 420 nm存在峰值。该波段的辐射主要来自于燃烧过程所产生的大量H2O。随着化学计量混合分数的增加,测量得到的H2O近红外波段内辐射强度逐渐降低。
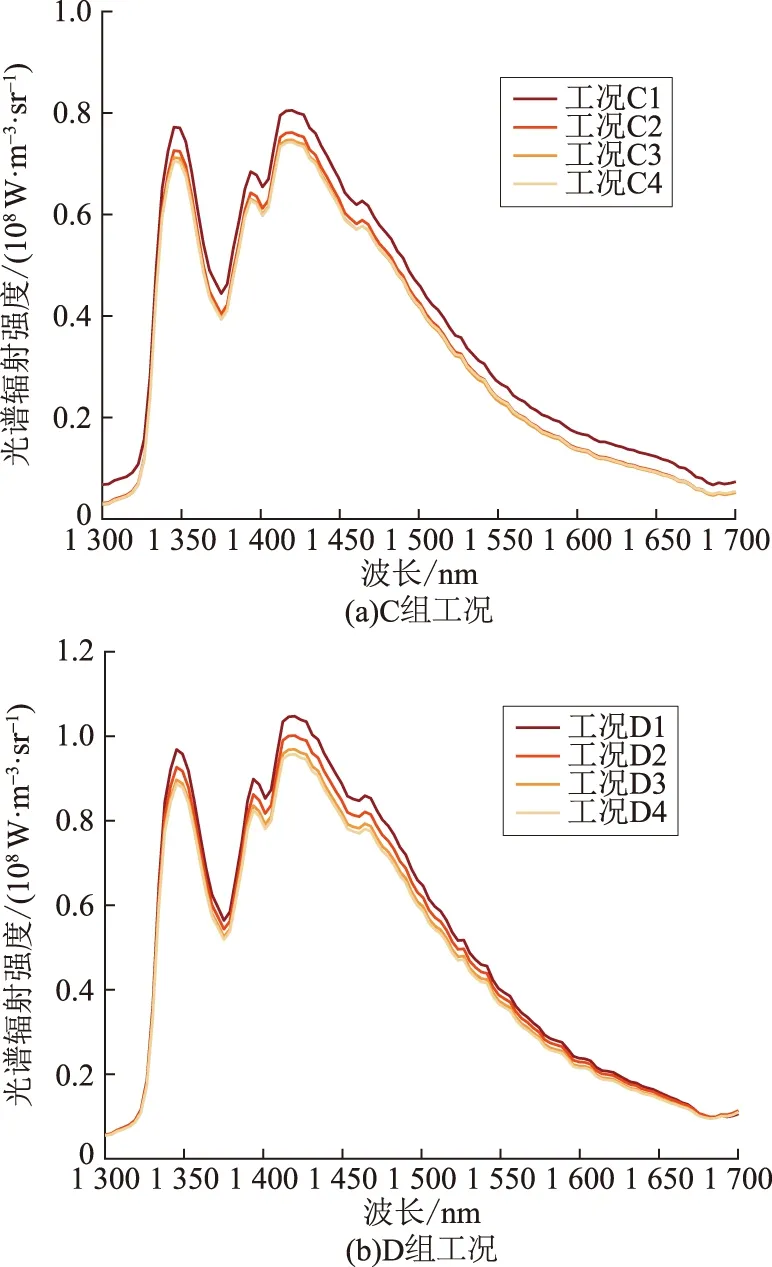
图5 测量得到各工况下的近红外辐射光谱Fig.5 Near-infrared radiative spectrum in each case
利用该方法得到的气体温度以及H2O体积分数如图6所示。从图6可知:C组工况火焰内的气体温度保持在2 241~2 308 K,而H2O体积分数保持在9.4%~10%;在D组工况中,火焰中气体温度与气体体积分数整体上升,火焰内的气体温度保持在2 448~2 461 K,H2O体积分数保持在9.5%~10.5%。
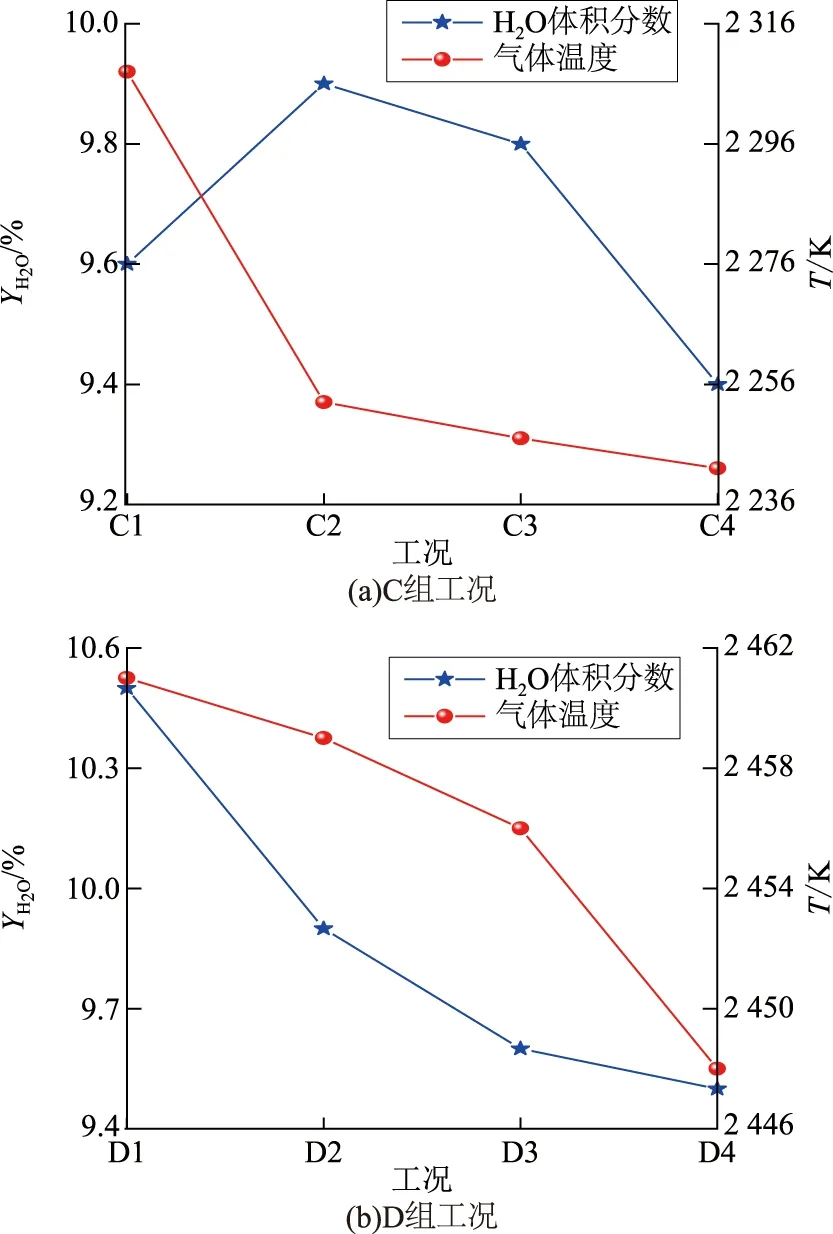
图6 测量得到各工况下的气体温度、H2O体积分数Fig.6 Gas temperatures and volume fractions of H2O in various cases
为进一步验证本文所提测量方法的可靠性,将本文方法所得到的结果与已有研究中燃烧数值模拟的气体温度、图像法测量的碳烟温度[27]进行对比,结果见表3。
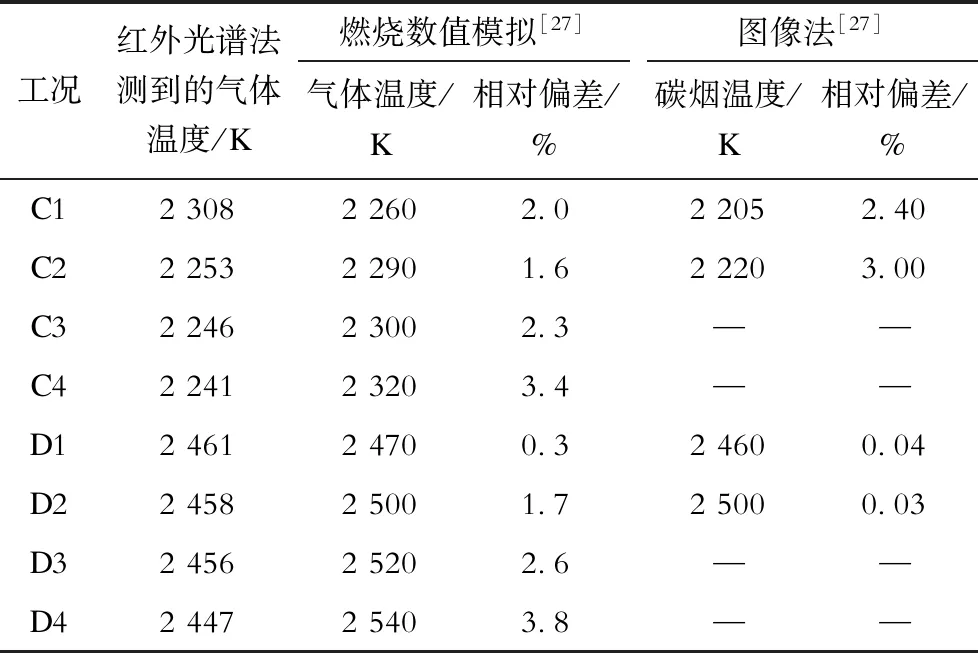
表3 3种方法获得的温度结果比较Tab.3 Comparisons of temperature results obtained by three methods
从表3可见,燃烧数值模拟的气体温度、图像法测量的碳烟温度与本文中红外光谱法测到的气体温度的相对偏差均小于4%,验证了本文方法用于气体温度测量的可靠性。
4 结束语
本文利用PSO算法,提出一种基于低分辨率红外光谱分析的燃烧气氛温度及组分体积分数的检测方法,并通过模拟反演计算验证了气体温度和体积分数测量结果的精确性。同时,基于近红外光谱检测技术,将该方法应用于富氧气氛下乙烯扩散火焰中气体温度以及H2O体积分数的测量实验,通过与燃烧数值模拟方法、图像法的对比,进一步验证了该方法用于气体温度测量的可靠性。

