水污染事故快速溯源方法及应急监测网络优化布设

胡玉珊，丁 涛，张舒羽，颜丹佳

(1. 浙江同济科技职业学院，浙江 杭州 311231；2. 中国计量大学 质量与安全工程学院，浙江 杭州 310018)

面对频繁发生的水环境污染事件，如何快速和精准地进行污染物溯源，尽快获知引发事故的污染源信息(排放位置、排放时间和排放量)，对实现水污染事故的靶向治理和制定有效的应急处置方案具有重要意义。近几十年来，在突发流域性水污染事故时，水域的水质得不到保障[1]，国内外已有很多学者在研究未知水体污染事件的溯源及污染源识别方面取得了一定的成果。这些研究大部分围绕确定性方法和不确定性方法的思路对河流水环境污染事件进行溯源研究与讨论[2-3]。水污染事故污染源识别的确定性理论方法包括直接求解法和启发式优化法。直接求解法是指将参数作为因变量，利用空间域和时间域上的导数信息，应用基于水质-水动力模型的反向计算法进行污染源信息求解的一种方法[4-10]。

水污染事故污染源识别的不确定性理论方法常采用随机方法。随机方法用概率分布函数来描述客观事故的随机性，包括统计归纳法[11]、贝叶斯推理法[12]以及最小相对熵(MRE)等。统计归纳法的优点在于能基于大量数据作不确定性分析，如Huang等[13]在收集钱塘江大量监测点数据的基础上，通过统计归纳分析得到钱塘江污染物来源的重点区域。最小相对熵(MRE)的优点在于对待求问题进行不确定性分析，即它能基于待求问题的先验分布获取待求问题的二次估计，如Woodbury等[14]率先将MRE应用于追溯地下水污染源信息以及重构大气污染历史。许多学者在基于传统贝叶斯推理的基础上加入MCMC抽样算法，通过以样本频率代替概率的方法得到污染源信息，通常称这种方法为Bayesian inference-MCMC算法。如Jiang等[15]通过直接MC抽样法，在反演污染源信息的基础上和溯源过程中公认的不确定性分析框架下，采用贝叶斯推理方法对扩散系数、流速等不确定性参数进行了敏感度分析及反演。Wei等[16]运用Bayesian-MCMC抽样算法，在污染源溯源过程中考虑算法中敏感参数的不确定性，消除了算法中敏感参数所带来的误差，得到了更加准确的污染源溯源结果。

从上述文献可知，目前水污染事故溯源研究中无论是确定性方法还是不确定性方法，其研究对象主要针对突发水污染事件的瞬时污染源，鲜见对持续排放的连续性污染源溯源方法的研究工作。而在现实环境中，水环境污染事件可分为两种，一种是瞬时污染事故，即在极短时间内通过大口径排放管道把大量污水排放到自然水体中，如运输化学品车辆倾覆或企业污水未经处理短时间大流量地直接排入自然水体；另一种是持续排放一段时间的污染事故，如化工企业在夜间的持续偷排或管道破裂引起的一段时间小流量污水泄漏事件等。因此，笔者针对连续排放的水污染事故溯源问题，基于二维对流扩散积分模型，研究提出了水污染溯源方法的理论公式，弥补和扩展了现有水污染事故溯源的方法体系。为使该理论公式能够应用于水污染溯源实践，同时研究构建了两点和四点对称应急监测网络的布设方式，通过构建的应急监测网络来监测和计算目标污染物浓度在空间域和时间域上的差分信息，得到优化布设方案，从而解决溯源方法向应用转化的关键问题。

1 二维对流扩散连续源积分模型

连续排放污染源溯源算法基于二维对流扩散连续源积分模型。在原点(0,0)处从t=0开始以速率为Q连续排放污染物，浓度为C0，因为是连续排放，可以视为一系列瞬时排放的叠加。

设在原点(0,0)处于t=τ时刻，经过dτ，注入的污染物排放量为dM=C0Qdτ，在(x,y)处，t时刻的污染物浓度为

(1)

式(1)中：C(x,y,t)为河流点的污染物浓度,mg/L；C0为连续源排放浓度,mg/L；Q为连续源排放速率,L/s；Dx，Dy分别为x，y方向湍流扩散系数,m2/s；t为时间,s；x为与排放污染源的水平距离,m；y为与排放污染源的垂直距离,m；u，v分别为水流在x，y方向的速度分量,m/s。

2 二维连续排放污染源溯源算法设计

式(1)通常用于二维对流扩散连续源信息已知的情况下，分析污染源排入河流后导致的污染物浓度变化情况。而在溯源反问题中，污染源信息(排放位置、排放时刻、排放速率)都是未知的。河流某固定监测点处的污染物浓度C，x和y方向上的弥散系数Dx和Dy，x方向上的流速u，y方向上的流速v均可由河流实际监测情况获得。通过这些可知量，利用式(1)的逆运算，可求得源强信息。因此，本文基于上面的思路，对二维对流扩散连续源积分模型式(1)进行一系列的逆向推导，来反向计算连续污染源的源强信息，那么式(1)可写为

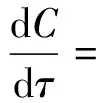
(2)

(3)

其中，C′是关于x,y,t的函数关系式，对C′(x,y,t)的x,y,t分别求导，得到

(4)

(5)

(6)

为了方便计算，将式(4)～式(6) 中的已知量设为

(7)

(8)

(9)

将式(7)～式(9)代入式(4)～式(6)中，求得

x=(u-a)×(t-τ)

(10)

y=-b(t-τ)

(11)

(12)

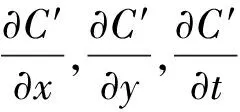
3 两点和四点对称应急监测网络布设方式

3.1 两点应急监测网络布设

图1为两点应急监测网络布设示意图，图中以污染源排放点为原点(0，0)，河流流向平行方向为x轴，河流流向垂直方向为y轴。在x方向上距离固定监测点P1的Δx处布置一个应急监测点P2，在y轴方向上距离固定监测点P1的Δy处布置一个应急监测点P3。

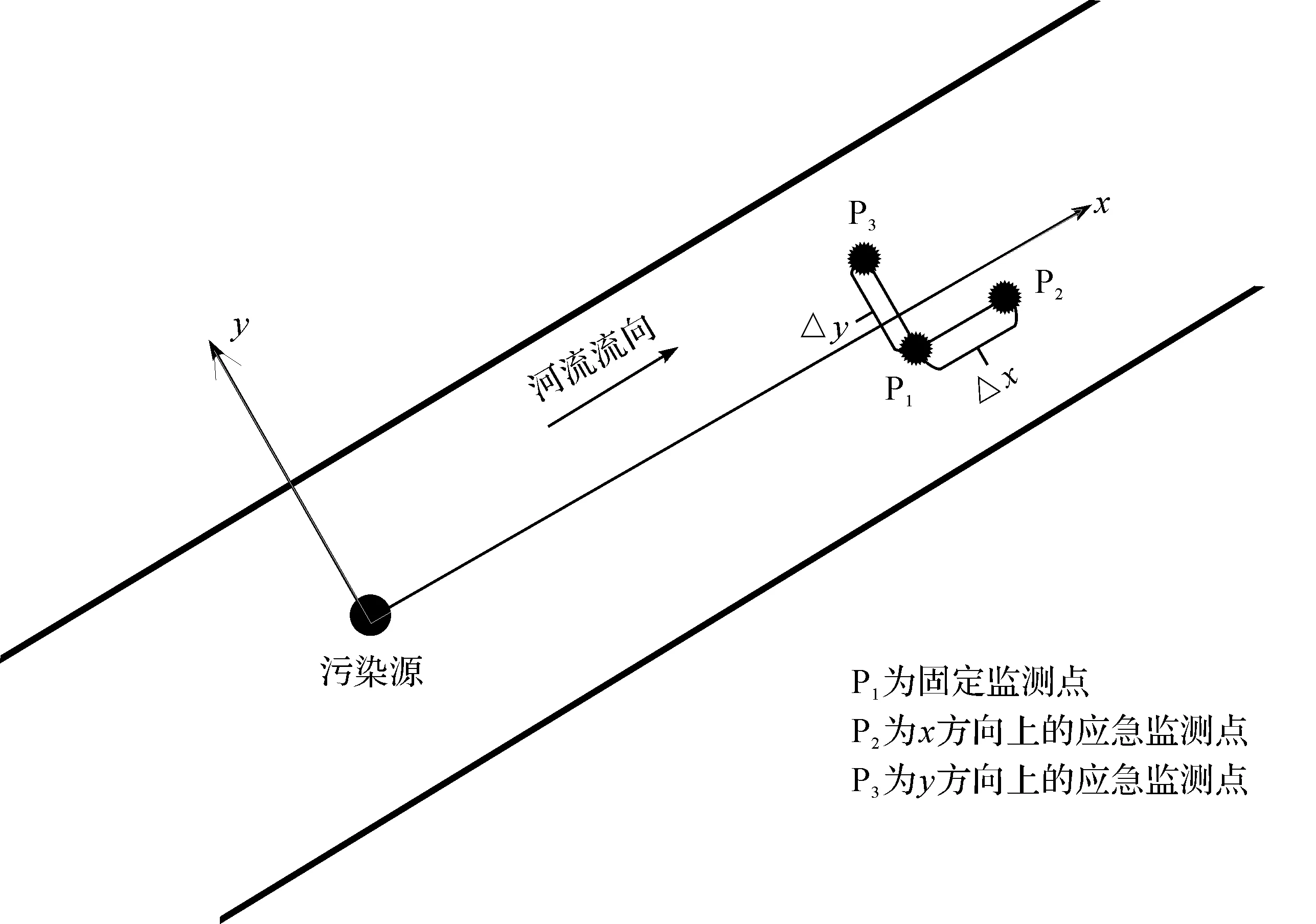
图1 两点应急监测网络布设示意

此时

(13)

式(13)中：CP1(T)为P1在T时刻的监测浓度；CP1(T+τ)为P1在T+τ时刻的监测浓度；CP2(T)为P2在T时刻的监测浓度；CP2(T+τ)为P2在T+τ时刻的监测浓度。

(14)

式(14)中：CP3(T)为P3在T时刻的监测浓度；CP3(T+τ)为P3在T+τ时刻的监测浓度。

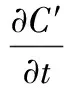
(15)

式(15)中：CP1(T+Δt)为P1在T+Δt时刻的监测浓度；CP1(T+τ+Δt)为P1在T+τ+Δt时刻的监测浓度。

连续排放污染源溯源算法工作步骤如下：

1)假设(0,0)处为污染源排放位置，河流下游固定监测点(X,Y)处监测到污染物浓度超标。

2)及时在x方向上与固定监测点P1相距Δx处布置应急监测点P2，在y方向上与固定监测点P1相距Δy处布置应急点P3。

3)在T时刻，P1，P2，P3同时测量河流水质，得到这三个点的污染物浓度，分别为CP1(X,Y,T),CP2(X+Δx,Y,T)，CP3(X,Y+Δy,T)。

4)在T+τ时刻，P1，P2，P3同时测量河流水质，得到这三个点的污染物浓度，分别为CP1(X,Y,T+τ)、CP2(X+Δx,Y,T+τ)、CP3(X,Y+Δy,T+τ)。

5)在T+Δt时刻，P1再次监测河流污染物浓度，为CP1(X,Y,T+Δt)。

6)在T+Δt+τ时刻，P1再次测量河流污染物浓度，为CP1(X,Y,T+Δt+τ)。

7)将上述步骤中测得的污染物浓度以及Δx，Δy，Δt，τ代入式(4)～式(15)，解得连续源信息的计算值x，y，t。将计算出来的x，y，t代入式(1)，可解得污染源排放速率C0Q。

3.2 四点应急监测网络布设

在x和y方向上设置对称应急监测点，即四点应急监测网络布设方法，示意图如图2所示。

图2 四点对称应急监测网络布设示意

此时

(16)

(17)

(18)

式(18)中:CP2(T),CP4(T)分别为同一时间x方向上与P1相距Δx处对称的两个应急监测点在T时刻的污染物监测值;CP3(T)，CP5(T)分别为同一时间y方向上与P1相距Δy处对称的两个应急监测点在T时刻的污染物监测值。CP1(T)和CP1(T+Δt)分别为P1在T时刻以及T+Δt时刻的污染物监测值。

溯源工作步骤如下：

1)假设(0,0)处发生突发水污染事故，河流下游固定监测点(X,Y)处监测到污染物浓度超标。

2)及时在x方向上与P1相距±Δx处布设应急监测点P2,P4，在y方向上与P1相距±Δy处布设应急监测点P3,P5。

3) 在T时刻，P1,P2,P3,P4,P5同时测量河流污染物浓度，得到它们在T时刻的污染物监测浓度值，分别为CP1(X,Y,T),CP2(X+Δx,Y,T),CP4(X-Δx,Y,T),CP3(X,Y+Δy,T),CP5(X,Y-Δy,T)。

4)在T+Δt时刻，P1再次监测污染物浓度，为CP1(X,Y,T+Δt)。

5)将CP1(X,Y,T),CP2(X+Δx,Y,T),CP4(X-Δx,Y,T),CP3(X,Y+Δy,T),CP5(X,Y-Δy,T)，CP1(X,Y,T+Δt)和Δx、Δy、Δt代入式(16)、式(18)以及式(7)、式(12)，获得污染源信息(X,Y,T)的计算值(x,y,t)，将计算出来x，y，t的值代到式(1)中，可解得污染源排放量。

4 研究实践与分析

笔者提出的河流水污染事故快速溯源方法是基于恒定流下污染物二维对流扩散方程的解析解，是在水文理想条件下的纯理论概化推导，目前研究阶段仅适用于人工输水河渠背景下的污染物溯源。笔者取温州地区瑞安市环城河马屿镇段作为研究对象，主要原因为：1) 瑞安市环城河是人工输水河渠，且河流湾道少，相对较直，符合研究需要的基本河道特性。2) 基于GIS的浙江省工业企业空间分布特征与水污染关系研究[17]，马屿镇工业发达，河流水污染事故发生概率较高，具有比较高的研究价值。

以瑞安市环城河马屿镇段河道为研究对象，讨论了两点对称应急监测网络布局参数Δx、Δy和T对溯源算法精度的影响，以及对比分析两点和四点对称应急监测网络布设形式。假设污染源以C0Q=0.01 kg/s的速率排入河渠的上游，参见图1，P1在x和y方向上与污染源位置相距X=5 400 m，Y=0 m，扩散系数Dx=50 m2/s、Dy=0.1 m2/s；河流流速u=0.5 m/s，v=0 m/s。P1在监测到污染物浓度超标时报警，系统需要通过应急监测网络布设和污染源溯源方法，进行溯源任务，得到连续源的排放速率Q，排放位置X和Y以及排放时间T的计算值。在溯源算法中，水深h，弥散系数Dx和Dy，流速u和v均为恒定值，而应急监测网络布设法中的参数T，Δx，Δy，Δt的值都是可变因子。

4.1 溯源计算与分析

从数学角度看，当Δx→0、Δy→0、Δt→0时，溯源结果最为准确。但由于现实条件限制，Δx,Δy,Δt不可能无限趋向于0。因此，设置了Δx,Δy的不同因子水平值。在不同因子水平下，通过比较溯源计算值和设计值之间的误差，得到优化的应急监测网络布设参数。

4.1.1Δx对溯源方法精度的影响分析

Δx取6个水平值，分别为1，5，10，30，100,300 m。其余参数取值如下：Dx=50 m2/s，Dy=0.1 m2/s，u=0.5 m/s，v=0 m/s，T=3.0 h，Δy=1 m，Δt=30 s，τ=30 s。通过溯源算法得到污染源信息的计算值，并计算溯源误差，结果如图3所示。

由图3可以看出，当Δx设置为1～300 m时，X的误差分别为3.25%，4.25%，5.29%，9.25%，20.89%,42.13%;T的误差分别为0.08%，1.16%，2.27%，6.51%，18.99%,41.74%;C0Q的误差分别为2.90%，4.00%，5.13%，9.41%，21.88%,44.14%。分析上述数据可得，Δx越小溯源误差越小。Δx在30 m以内的溯源误差小于10%，在可接受范围内。而随着Δx的增大，误差越来越大，会严重影响溯源精度。

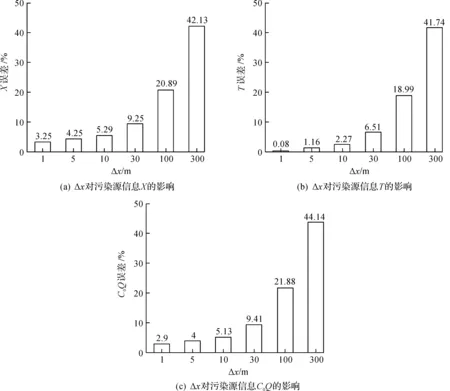
图3 应急监测网络参数Δx对溯源算法精度的影响

4.1.2Δy对溯源算法精度的影响分析

Δy取5个水平值，分别为1，5，10，30,100 m。其余参数取值如下：Dx=50 m2/s，Dy=0.1 m2/s，u=0.5 m/s，v=0 m/s，T=3.0 h，Δx=1 m，Δt=30 s，τ=30 s.通过溯源算法得到污染源信息的计算值，并计算溯源误差，对溯源算法精度的影响计算结果如图4所示。

图4 应急监测网络参数Δy对溯源算法精度的影响

由图4可以看出，当Δy设置为1～100 m时，X的误差分别为3.25%，3.37%，3.75%，6.97%,10.91%;T的误差分别为0.08%，0.21%，0.60%，3.92%，7.97%;C0Q的误差分别为2.90%，2.91%，2.91%，3.02%,3.31%。分析上述数据可得，Δy越小溯源误差越小。当Δy为100 m时，其X值的相对误差为10.91%，在可接受范围内。因此，对于应急监测网络中的Δy可以不做太高要求。

4.1.3 T对溯源算法精度的影响

T分别取1.0 h(代表污染团远未到达P1点)、2.0 h(污染团前端到达P1点)、3.0 h(代表污染团中心到达P1点)、4.0 h(代表污染团尾翼到达P1点)、6.0 h(代表污染团远离P1点)。其余参数取值如下：Dx=50 m2/s，Dy=0.1 m2/s，u=0.5 m/s，v=0 m/s，Δx=1 m，Δy=1 m，Δt=30 s,τ=30 s。通过溯源算法得到连续源信息的计算值，并计算溯源误差，结果如图5所示。

图5 T对溯源算法精度的影响

由图5看出，在T=1.0 h时，污染还未到达监测点，此时溯源误差非常大;在T=2.0 h时，监测点受污染的影响较小，此时溯源误差仍比较大;在T=3.0 h时，溯源误差是最小的，此时污染团中心接近固定监测点，对监测点的影响最大，溯源结果最为可靠。根据二维对流扩散连续方程，污染物浓度在后期将保持不变。因此在T=4.0 h之后，应急监测网络的浓度差将缩小，导致溯源误差增加。

4.2 应急监测网络布设形式对算法精度的影响分析

以应急监测网络参数Δx为例，分析四点对称应急监测网络布置法对溯源误差的影响，并将结果与二点应急监测网络布置法进行对比。Δx取值分别为1，5，10，30，100，300 m。其余参数取值如下：Dx=50 m2/s，Dy=0.1 m2/s，u=0.5 m/s，v=0 m/s，T=3.0 h，Δy=1 m，Δt=30 s，τ=30 s。通过溯源算法得到污染源信息的计算值，并计算溯源误差，结果如图6所示。

图6 应急监测网络布置方式对溯源精度的影响

由图6可以看出，四点对称应急监测网络布设法相比二点法，溯源误差都要小，说明设置对称应急监测点可以降低溯源误差。且在同一T下，溯源误差随着Δx的增大变化不大，说明设置对称应急监测点可以提高溯源误差的稳定性。因此，在条件允许的情况下，采用四点对称应急监测网络布设法明显优于两点应急监测网络布设，从而降低溯源误差。

笔者提出的河流水污染事故快速溯源方法是在恒定流污染物二维扩散方程解析解(式(1)的基础上逆向推导得到，是水文理想条件下的求解方法。因此，目前溯源方法的研究成果仅适用于满足恒定流条件的人工顺直输水渠道，不适于水深、流量和流速等水力要素随时间和地点变化的自然河道。为促进该方法由理论分析向应用转化，应进一步开展如下研究工作：应结合室内瑞安市环城河马屿镇段水槽模型进一步开展算法的验证性工作；加强污染物测量误差对溯源精度的影响分析。目前方程中仅考虑了污染物随水流的迁移和扩散作用，未考虑污染物的沉降、再悬浮、吸附和降解等作用，应加强该部分的研究工作。同时，将研究成果应用到瑞安市环城河马屿镇段的实际监测中，并不断矫正参数，达到可用可塑的目的。

5 结 论

1)提出了河流二维连续排放污染源的溯源算法，实现了对河流二维对流扩散方程的反向求解，解决了污染源位置、释放强度和释放时间等源强信息计算的理论公式问题。笔者提出的两点对称和四点对称的河流应急监测网络的布设方法，解决了目标污染物浓度在空间域和时间域的差分计算问题，从而为河流二维连续污染源的溯源算法的应用奠定了基础。

2)应急监测网络影响因子Δx，Δy，T等对溯源误差的影响趋势相同。相对而言，Δx和T对溯源精度的影响更大，Δy对溯源精度的影响较小。固定监测点与污染团中心的相对位置对溯源精度影响很大。在污染团中心接近或到达常设监测点时，运用该溯源方法的相对误差最小。应急监测网络中应急监测点的位置离常设监测点越近，相对误差越小。四点对称应急网络布置法与二点应急网络布置法相比，相对误差更小，且当布置条件发生改变时，四点对称应急网络布置法的溯源误差稳定性更高。

3)通过将瑞安市环城河马屿镇段作为实际研究对象，设计的污染场景以及不同应急监测网络布局形式下污染源设计值与计算值的相对误差计算，验证了溯源算法的可行性。该溯源方法可提高对水污染源事件的应急响应能力，有效并快速地为污染处理提供科学的理论依据。

4)在实践应用中，应开展算法的验证性工作，分析水环境条件、模型参数和测量误差等要素对溯源的影响，进一步完善和论证溯源方法的可行性和可靠性。