基于知识数据化表达的制冷空调系统故障诊断方法

孙哲，金华强，李康，顾江萍，黄跃进，沈希，2

（1 浙江工业大学机械工程学院，浙江 杭州 310014； 2 浙江农林大学光机电工程学院，浙江 杭州 311300；3 浙江工业大学教育科学与技术学院，浙江 杭州 310014）

引 言

随着近年来能源与碳排放问题的突显，世界各国纷纷制定自己的能源战略，我国也将能源战略放在了突出的位置，提出了“碳达峰·碳中和”的战略目标[1]。制冷空调系统主要用于建筑的环境调节，也可用于工业环境控制，其能耗已成为建筑能耗的重要组成部分，约占社会能耗总量的20%[2]。由于制冷空调系统结构复杂、设备种类繁多，存在多种热质交换和功热转换形式，在运行过程中不可避免会发生各类故障。相关研究表明，制冷空调系统故障运行会造成15%～20%的能耗增加[3]。

长期以来，空调系统的运行维护管理以“定期检修+报警抢修”模式为主，盲目性高且难以发现隐性故障。通过人工智能的方式可极大提高故障特征的自主辨识，实现全时段智能监控，降低对运维人员专业素养的依赖[4]。制冷空调系统是一类复杂的热力系统，故障状态下系统的热力参数会较原状态产生偏离，即故障的热力学征兆，如温度升高、压力降低等。偏离后的热力参数值不仅与故障状态有关，同时受环境、负荷、工况等诸多因素影响，使得故障和征兆之间的关系不仅复杂而且存在不确定性。这种故障-征兆的复杂映射关系给故障诊断规则制定带来极大挑战，使得基于规则的故障诊断方法难以保证精度。以深度学习为代表的数据驱动方法凭借其强大的特征提取能力，可以较好地解决复杂热力系统的诊断难题。Sun 等[5-6]针对热泵空调系统的深度学习故障诊断方法展开研究，提出一种基准模型+深度卷积网络的诊断框架，实现了系统偏离特性的高效提取，很好地提升了复杂热力系统的诊断精度。Wang 等[7]面向现场应用场景展开诊断方法研究，利用贝叶斯网络实现特征高效筛选，解决了现场诊断传感器数量少、成本受限等实际问题。van de Sand 等[8]针对冷水机组故障诊断问题，提出一种基于区域自适应的数据驱动诊断方法，缓解了监督学习对标记样本的依赖。刘旭婷等[9]针对冷水机组提出一种基于稀疏局部嵌入深度卷积网络的故障诊断方法，采用稀疏局部嵌入代替卷积核，有效避免了复杂的训练和调参。王路瑶等[10]基于长短时记忆神经网络提出一种空调系统传感器故障检测方法，有效缓解了大滞后系统时序建模精度低的难题。Xiao 等[11-14]较早提出了基于贝叶斯网络的诊断框架，大量研究成果为学科后续发展提供极具价值的新思路。Li 等[15-17]提出一系列基于深度学习的智能诊断算法用于解决多联机、空气源热泵、热泵热水器等诸多装置的故障诊断问题。

数据驱动方法的优势在于可以从数据中自学习复杂映射关系，这就使得其对标记样本的质量和丰富度具有严重依赖，而真实应用场景中足质足量的标记样本往往难以获取。随着智能化技术逐步走向应用，解决标记数据依赖问题已成为当下研究的重中之重，近两年来越来越多的学者[18]针对这一问题展开研究。将机理知识融入数据驱动不仅可以降低对标记数据的依赖，同时可以提高诊断方法的鲁棒性和可靠性。张钹等[19]指出，将机理知识融入数据驱动是新一代人工智能发展的必经之路。制冷空调系统故障诊断的实质是通过对系统表现的征兆进行模式识别而得出诊断结论，故障和征兆的定性关系可以通过热力学分析得出，其征兆的规律性描述正是诊断模型的诊断依据。因此，通过故障规律性知识指导实现故障的模式识别，在理论上是可行的。然而，实际情况中，制冷空调系统常面临环境多变、负荷多变以及控制需求多变的问题，导致其运行工况持续处于动态过程。动态条件下的系统征兆也会随之变化，使得故障和征兆的映射关系出现不确定性，这种动态征兆是难以通过热力学精准分析的。如何利用定性的静态征兆知识指导实现动态系统的故障诊断是一个非常困难的问题。

本课题组前期研究发现，制冷空调系统故障征兆的实质是热力参数偏离正常基准，多变工况下参数偏离的方向一致，其差异在于偏离大小。例如高负荷下相同故障的参数偏离量更大。利用热力学机理分析容易得到故障条件下参数的偏离方向，但却难以针对所有工况预测出偏离大小。而事实上，诊断的目标只是将故障类别识别出，无论何种偏离程度均对应同一类故障结果。如果利用一种随机生成的策略在偏离方向的基础上获得不同偏离大小的伪样本，则相当于得到了不同工况下系统故障的标记数据，进而解决标记样本不足的问题。因此，本文提出一种基于知识数据化表达的制冷空调系统故障诊断方法。首先，通过机理分析构建故障的定性偏离矢量，然后通过一种数据随机缩放策略实现知识的数据化表达，达到信息扩增的目的。在实施诊断时为了将真实系统的热力参数转换成生成样本的偏离形式，提出一种基于基准模型的偏离特性的表征策略。最终，以知识驱动代替标记样本实现制冷空调系统的故障诊断。

1 制冷空调系统故障诊断知识的数据化表达

制冷空调系统故障状态的表现形式是热力参数的偏离，这种偏离包含大小和方向两部分。对于同一种故障而言，不同系统间以及同一系统在不同条件下的特征偏离方向是一致的，不同点在于偏离大小，其受到系统结构、环境条件和运行工况等不同因素的影响。如果要精确计算出理论上的偏离大小无疑是十分困难的。而事实上，故障诊断完全可以仅依赖不同热力参数的偏离方向进行识别。因此，定性的偏离知识表达理论上是可以支撑故障诊断的。可以通过热力学分析、数值仿真、实验测试等手段获得特定系统的故障定性偏离规律，这种规律是模糊的偏离方向和偏离程度，如参数1偏大且偏离程度为严重。详细的偏离知识示例见3.1节。

这种定性的规则较早被应用到制冷空调系统故障诊断中，称之为基于规则的诊断方法[20]，然而精度均不理想，导致这种结果的原因是制冷空调系统复杂且多变，故障和征兆之间的映射关系不仅高度非线性且具有一定的不确定性。而数据驱动方法可以通过学习数据分布中的深度特征而实现故障-征兆间复杂映射关系的拟合，其诊断精度远高于基于规则的方法。因此，2010 年以后，绝大多数制冷空调故障诊断研究都聚焦于数据驱动方法[21-25]。如果能将制冷空调系统故障的定性偏离规律以数据的形式表达并通过信息扩增手段丰富其信息量，则可以在不依赖真实标记数据的条件下充分利用数据驱动优势。

故障状态参数偏离的表示形式可以称之为故障诊断知识的多维偏离矢量，每一个参数既含有方向又含有程度，如果对不同的偏离程度赋予特定的值，则从数据的角度可以将其看作一条标记样本。然而仅利用这一条标记样本显然无法满足数据驱动模型的训练。如何对多维偏离矢量的信息进行扩增，是亟需解决的问题。由于不同偏离大小代表不同情形下的故障数据，这种情形越多代表数据的信息越丰富。在一定的范围内对赋值后的多维偏离矢量进行缩放则可以模拟生成不同情形下的标记数据。本文提出一种数据随机缩放策略，基于多维偏离矢量生成大量伪数据，用于深度模型训练。数据随机缩放策略的目的就是使多维偏离矢量各个维度经过等比放大或缩小，实现不同偏离量的模拟。缩放策略的目的是增加矩阵数据的信息熵，以提高深度模型的学习效果。偏离数据是故障模式识别的依据，其主要特征在于偏离方向和偏离大小，对于深度模型而言，相同的偏离方向下不同的偏离幅值对模型分类具有明显影响。不同制冷空调系统由于运行工况、所处环境以及故障严重程度的差异，同一种故障的偏离幅值存在差异，用于训练的数据需要尽可能多地包含不同偏离幅值样本。数据缩放策略就是基于这一思路，对矩阵数据乘以缩放系数后得到放大或缩小的矩阵样本，如式(1)所示。

多时间步多维度的偏离数据构成矩阵数据，矩阵数据的所有元素均等比缩放，得到新的样本。这里缩放前的矩阵数据可以是真实偏离矩阵也可以是人工赋值的偏离矢量。通过多个缩放系数对矩阵数据缩放可以得到多组新的矩阵数据，例如利用0.5、0.75、1.5、2.1 四个缩放系数对同一矩阵数据缩放就可以得到四个新的矩阵数据。缩放系数在设定的缩放范围内随机取值，而缩放系数的个数取决于诊断模型所需的训练样本数，这通常可以根据神经网络模型的大小而确定，例如训练样本需要包含每类故障3000 组样本，则在缩放范围内随机生成3000个缩放系数。

图1 是以三类故障为例对缩放策略进行描述，每类故障选取四个特征(蒸发温度TRE、冷凝温度TRC、吸气温度T_suc、排气温度TR_dis)，每一行代表一个时间点，每个样本是6×4矩阵数据，这里具体数值是根据偏离矢量设定的偏离值，每类故障对应一个偏离矩阵。图1 中分别为3、0.5、1.5 这三个缩放系数生成的三个样本，该样本作为诊断模型的输入。图中的缩放过程与上文描述有两处不同：(1)红色参数并没有进行缩放；(2)每个缩放后的数值均添加了一个较小的随机数。

图1 数据随机缩放策略Fig.1 Data random scaling strategy

由于真实样本具有一定的不确定性，简单利用缩放系数进行伪样本生成，其效果是不理想的。本文进一步提出对生成样本添加标准正态分布的高斯噪声，丰富数据的信息复杂度，以此提升模型准确性和鲁棒性。标准正态分布是最符合自然界真实分布的，利用该类噪声可以更好地模拟系统真实扰动。噪声添加策略使性能得到提升的原因主要有两个方面：(1)真实残差数据本身是有较大随机波动的，单纯的等比缩放与真实情况不符，高斯噪声模拟的是系统的随机扰动，而偏离量模拟的是系统偏离正常工况，二者叠加则表示不同随机扰动下系统均呈现一种固定的偏离模式，而故障诊断的目的就是识别这种模式，使生成分布与真实分布更接近；(2)添加噪声实质是添加扰动，这种思路借鉴了神经网络中的Dropout 层[26]，该网络层通过随机失活部分神经元以实现扰动添加，使神经网络学习过程得到强化，从而有效避免神经网络过拟合，是公认的提升神经网络鲁棒性的方法。本文借鉴这一思路以添加噪声的方式强化神经网络学习过程，使得模型更加聚焦于偏离规则这种共性特征。同时，噪声的添加强度对诊断结果影响较大，弱噪声起不到模拟扰动的作用，强噪声则会引入过多的干扰从而降低诊断精度，因此，需要实验验证最优的噪声添加强度。

此外，本文还提出随机缩放策略有三个关键的技巧，可以保证其有效实施。(1)并不是所有特征都进行缩放，不产生偏离的特征不进行缩放，这些不偏离的特征可以根据故障自身的规律人为指定，如图1 中红色数据，以避免非偏离参数的误差被放大强化。(2)不产生偏离的特征要设置一个小于1 的值，比如0.1，实验证明这样比1 的效果好很多。(3)缩放系数的生成范围设定非常关键，缩放范围需要考虑目标系统可能出现的严重程度，越严重的故障偏离量越大，而这种偏离量可以根据经验估算。缩放后的偏离数据的上下限应包含所有故障程度下的偏离范围。例如目标系统可能出现的冷凝温度最大故障偏离小于5℃，最小故障偏离大于1℃，设定的该偏离矢量值为2，则缩放范围需覆盖(0.5,2.5)。由于多维偏离矢量的不同参数缩放范围可能不同，最终的统一缩放范围应取大。经过随机的缩放后，生成的伪数据包含了各类情况下的系统故障信息，以此训练深度模型可以很好地保证其在实际诊断时的适用性。这一过程的实质就是实现了故障诊断知识的数据化表达，其完整的流程见图2。

图2 知识的数据化表达流程Fig.2 The expression process of digitized knowledge

2 基于知识数据化表达的制冷空调系统故障诊断方法

基于数据化的知识实现完整的制冷空调系统故障诊断流程见图3。方法分为两个部分。(1)模型训练：使用数据化的知识训练诊断模型，使之得到故障诊断的划分边界，训练完毕的模型用于诊断目标系统故障类别。(2)诊断实施：通过偏离特性表征策略，使真实运行数据以偏离残差的形式表征，这种表征形式和数据化的知识形式相同，从而使得诊断模型可以对其进行诊断分类。

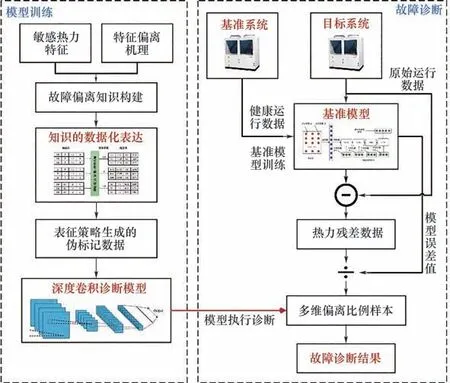
图3 诊断总体流程图Fig.3 The flowchart of proposed method

2.1 生成样本一致性评估方法

第1节中利用随机缩放策略实现了知识数据化表达，生成了带有标记的伪数据，这种生成数据的质量高低决定了训练模型的诊断效果。因此，首先要对生成样本的一致性进行评估，目的是为了获得和真实分布差异最小的生成样本。

对于数据分布的距离评估有很多种方法，如核最大平均差异(kernel maximum mean discrepancy，MMD)[27]、瓦瑟斯坦距离(Wasserstein distance)[28]和弗雷歇距离(Fréchet inception distance，FID)[29]等。其中MMD 距离最常用于估计两分布差异[30]。在固定的核函数下，MMD指标用于度量真实分布和生成分布的差异，MMD 值越小，代表两分布差异越小。MMD指标可以定义为式(2)：

式中，Pr和Pg分别表示两个待度量分布；xr和xg为分布中具体样本；k是映射函数。xr和xg分别理解为两个不同数据集内的数据样本，式(2)的目的是寻找一个映射函数k，使得计算出的所有样本平均距离有最大值，即得到了MMD 值。通过MMD 评估对知识数据化表达策略进行优化，最终实现生成样本的质量最优。

2.2 目标系统偏离特性的表征策略

生成数据其实质是系统热力参数偏离特征，而目标系统直接采集的运行数据是真实的热力值。如果要使用生成数据训练模型诊断目标系统，则必须将目标系统的数据以偏离特征的形式予以表征。偏离特征是指故障状态下热力参数偏离理论正常值，获取偏离特征则首先需要精准得到理论上的基准值。热力参数受到多种因素影响，呈现非线性、强耦合的特征。如排气压力这一热力参数不仅与系统结构和工质有关，还与环境温度、负荷大小、控制目标温度等多种因素有关。要想在考虑众多因素的情况下准确预测热力健康值是十分困难的。本课题组前期提出一种基于深度神经网络的制冷空调系统基准模型[5]，该模型融合卷积网络、编-解码器、循环神经网络，以数据驱动的方式解决了大滞后、强耦合系统建模困难的问题，模型结构如图4所示。该模型处理时序数据，每个样本包含前置时间段(t1～tn)和预测时间段(tn+1～tn+m)。前置时间段仅包含状态参数，通常为10～15个时间步长，预测时间段包含之后的时间步的输入参数，结合后续诊断模型要求的数据结构，预测时间段可以是10～20 个时间步长。前置时间段的数据是二维矩阵数据(参数个数×时间步长)，表征预测开始前一段时间系统的持续状态，对大滞后系统预测具有重要作用，这里使用卷积网络处理前置时间段数据并输入到编-解码器。通过解码器将前置状态信息编码到固定长度的向量并输入到循环神经网络，作为该网络的初始值，可以较好地继承预测时间段开始时刻系统所处的状态。循环神经网络根据每一个时刻的输入变量预测对应时刻的状态变量，最终实现多步状态变量的预测。详细的模型介绍和实验分析可以参考文献[5,30]。模型的输入为系统的外界自变参数，包括环境参数、控制参数、负载参数，例如环境温度、压机转速、膨胀阀开度、风机转速等。输出的预测值为系统的因变参数，主要包括系统各类温度、压力等热力参数，通常为故障的敏感特征参数。具体的输入输出变量需要根据数据集确定，本文使用的参数选择方案见3.1 节。基准模型利用健康系统采集的运行数据训练，实现健康系统的拟合，属于回归建模问题。由于健康运行数据通常容易获取，因而该训练策略不会限制基准模型的实际应用。

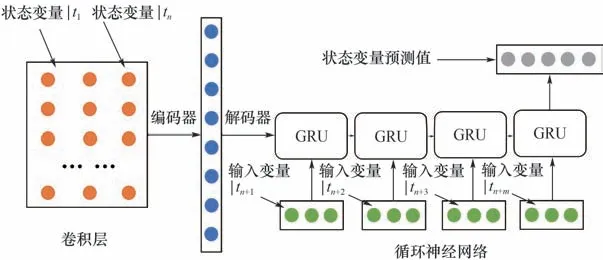
图4 制冷空调系统基准模型结构Fig.4 The structure of refrigeration and air-conditioning system benchmark model

利用该基准模型实现制冷空调系统基准预测，并以此计算出目标系统参数偏离量，即实现了运行数据向偏离特征的转换。此时的偏离值是真实的偏离值，但不同热力参数的偏离值含义不同，如排气压力偏离0.1 MPa 已经偏离很大了，而排气温度偏离0.5℃都不算大，这是由于不同参数的量纲不同。为了保证所有偏离量的含义相同，需要对其去量纲化。这里使用基准模型的每个参数下的误差作为量纲去除的系数，误差可以在验证数据集上通过对基准模型预测值和真实值求平均差得到，例如在健康数据集中基准模型对排气温度的预测误差为0.5℃，则对每个真实的排气温度残差除以0.5，得到统一的去量纲偏离量。具体表征策略如下。

第一步：获取系统的热力基准信息。即得到系统各特征参数健康状态下的理论值，该理论值受到环境、工况、负荷等多因素的共同影响。

第二步：获取敏感特征的残差值。即将第一步获取的基准值和系统实测值做差，得到的差值的实质是热力偏离量。

第三步：计算残差与基准误差量的比值。基准值获取依赖预测模型，其自身带有一定误差，使得不产生偏离的特征亦会产生较小的残差量，该值可以通过训练数据集计算得到。通过计算残差和误差的比值可以清晰得到偏离倍数，同时对不同量纲实现统一。

本文提出的使用人工生成的偏离参数作为模型的训练数据的方法，诊断实施时同时需要将目标系统的运行数据转化为偏离残差，而不是直接使用实际运行数据。其主要原因及优势为：(1)偏离残差的本质是故障特征，以偏离的形式表征故障可以极大降低数据的复杂度，抵消热力系统自身滞后性和非线性对诊断带来的影响，从而提高诊断精度。该结论在前期研究工作中已证明[5]。(2)本文利用生成数据代替真实标记数据以解决标记数据不足的问题，利用故障热力学偏离规律可以生成偏离残差，但却无法生成真实的运行数据。因此，要想实现知识数据化表达，这种数据必须是偏离残差数据。

2.3 基于卷积神经网络的故障诊断模型

第1节介绍了数据缩放策略以实现知识的数据化表达，随着生成数据量的增多，生成数据分布和真实数据分布的重合度会随之增加，但仍然不会完全重合，这就需要诊断算法具备一定的扩展性。深度神经网络通过多层复杂变换处理样本深层特征，可以较好地对样本分布进行扩展。残差数据是典型的多维时序数据，可以将其认为是一种矩阵数据。因此，诊断模型使用深度卷积网络搭建，以充分利用其对矩阵数据复杂特征的学习能力，具体结构见表1。模型使用生成的伪数据训练，从而解决对真实标记数据的依赖。实施诊断时，将目标系统的数据经过2.2 节方法转化后输入模型，模型输出即为故障预测类别。矩阵数据的列数等于敏感特征的数量，而行数是截取的时间步长度，通常会根据敏感特征数据选择时间步长度，使其行列数接近。

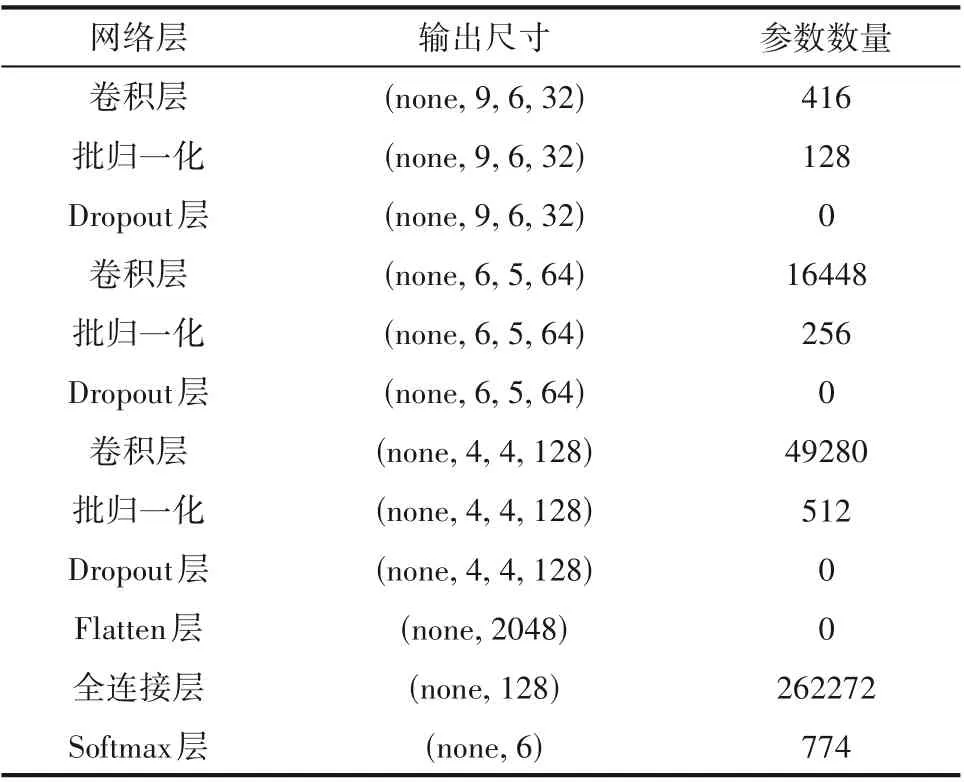
表1 深度诊断模型网络结构Table 1 The network structure of deep diagnosis model

3 实验数据集与平台

3.1 实验数据集

本文利用ASHRAE RP-1043 数据集进行实验研究[31]。ASHRAE RP-1043 是美国供暖、制冷与空调工程师学会于1999 年启动的项目，全名为fault detection and diagnostic (FDD) requirements and evaluation tools for chillers，旨在建立一个用于制冷系统故障诊断研究及方法评估的数据集，该数据集包含不同负载、不同故障条件下的制冷装置瞬态和稳态的运行数据。项目测试系统为一台制冷量为90 冷吨(316.5 kW)的离心式制冷机组(图5)，使用R134a 制冷工质，机组安装在70℉(21.1℃)的恒温室中。该数据集是一个常用的公开数据集，以此作为实验数据集可以较好地验证提出方法的有效性。

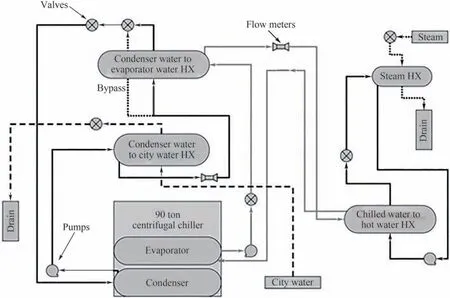
图5 制冷机组结构原理图[31]Fig.5 Schematic diagram of chiller structure[31]

本文选择项目中6 类故障和1 类健康数据，每类故障包含4 种不同严重程度。这6 类故障分别是：冷凝器结垢(cf)、冷却水流量减少(fwc)、冷冻水流量减少(fwe)、含非凝性气体(nc)、制冷剂泄漏(rl)、制冷剂过充(ro)。每种故障不同严重程度的模拟条件见表2。

表2 不同严重程度故障的模拟条件Table 2 Simulated conditions for faults of various severity

针对这一数据集，Comstock 等[32]对其特征的敏感程度及其偏离特性进行了研究，选定了7 个关键特征用来表征故障，分别是：蒸发器进出口水温差(TEI-TEO)、冷凝器进出口水温差(TCO-TCI)、蒸发器压力(PRE)、冷凝器压力(PRC)、过冷度(TRCsub)、吸气过热度(Tshsuc)、排气过热度(Tshdis)。并建立了不同故障下特征参数的偏离矢量表(表3)，这一表格就是故障偏离特性的定性知识表达。本文根据这一知识进行诊断，而在现实诊断过程中亦可以通过理论推演、人为经验等多种方式获取定性知识表达。

表3 故障的多维偏离矢量Table 3 Multi-dimensional deviation vector of failure

由于偏离特性的表征需要用到基准模型，根据2.2 节中对基准模型的介绍，需要从ASHRAE RP-1043 数据集中分离出用于基准模型输入输出的变量集。基准模型的输出变量就是上述7 个故障特征，而输入变量应该是系统的自变量，包含环境相关变量及控制相关变量，具体包括：蒸发器入水温度、冷凝器入水温度、交互换热器冷凝侧入水温度、交互换热器冷凝侧出水温度、交互换热器蒸发侧入水温度、交互换热器蒸发侧出水温度、外部入水温度、外部出水温度、热水入水温度、热水出水温度、冷凝器水流量、蒸发器水流量、小型蒸汽阀开度、大型蒸汽阀开度、三通阀开度、外部水阀开度。

3.2 算法运行环境

深度学习算法使用Tensorflow 和Python 编程实现，版本分别为2.6.0 和3.9.7，开发环境为Pycharm 2018。GPU 加速算法使用CUDA11.2 和cuDNN8.1支持库。算法的运行平台为一台图形服务器，GPU是NVIDIA GeForce RTX 3080Ti，CPU 是Intel i9-11900K，内存为64 G，操作系统是64位Windows 10。

4 实验与分析

本节对前文提出方法进行实验分析。首先，针对目标系统训练基准模型，进而实现偏离表征，获取后续对比实验所需格式的真实样本。然后，利用MMD 算法对生成样本和真实样本的一致性进行评估，验证最优数据生成策略。进一步，利用生成数据训练诊断模型并在真实数据集上验证分析，得到最佳诊断策略。最后，与当下主流的监督学习对比，验证提出方法的有效性和优势。

4.1 目标系统数据的偏离表征

目标系统数据的偏离表征依赖基准模型实现，基准模型的精度决定了表征的准确性。参照图4构建基准模型，并利用目标系统的健康运行数据训练，使之可以良好地拟合健康系统动态特性。模型使用12000组样本训练，每组样本的时间步长为12，并在3000 组不参与训练的测试数据集上验证模型精度。模型的输入参数为环境和控制相关变量，决定了系统的外部条件，这里使用3.1 节中选定的输入参数。输出参数为热力状态参数，是受外部条件作用下的系统表现，这里选择的是表3 中的7 个关键参数。使用Adam 优化器和MSE 损失函数，训练100 轮后，测试数据集上的损失值为0.0015。在3000 组健康测试样本上进行模型误差计算，得到7个关键参数的误差绝对均值(表4)。这里误差均值是3000组样本上预测值和真实值的平均偏离量，如TEI-TEO 的误差均值为0.045，代表基准模型对该参数预测的平均误差为0.045℃，可见预测精度已非常高，远超物理模型的预测精度。

表4 基准模型的预测误差绝对均值Table 4 The absolute mean of the prediction error of the benchmark model

利用训练好的基准模型对目标系统的状态值进行预测，得到目标系统所处环境和控制条件下理论参数的健康基准值，并与实测值进行做差，得到偏离残差值。进一步去量纲化，将残差除以表4 中基准模型误差，得到偏离比例系数，其数学表达见式(3)。

式中，y表示偏离比例系数；yreal表示真实值；ypre表示预测值；err表示模型误差值。这种比例系数的形式与生成的伪数据形式一致，实质上伪数据就是为了模拟偏离比例系数。

由于偏离比例系数通常大于1，对于一些严重的故障，偏离比例系数可能达到20，神经网络对这种数据不太适用，需要进行归一化处理。深度学习中的归一化包括两类：严格归一化、非严格归一化。利用arctan 等函数将数据严格限制到小于1 的方式属于严格归一化，这种方式适用于无法处理大于1的算法。然而，这种归一化对数据进行了非线性处理，使得部分数据区间的差异被放大或缩小，给算法识别带来难度。而非严格归一化则不会强制限定到1 以内，其处理方式更加自由。本文使用线性归一，对所有偏离数据除以5，属于非严格归一化。系数5是根据经验设定，该值与系统制冷量有关，通常制冷量越大该值应该越高，使处理后的数据最大值接近1。这种线性归一可以使数据范围更加收敛，同时最大程度保留原有数据的有效信息。

4.2 基于MMD的生成样本一致性评估

基于随机缩放策略的数据生成需要首先进行多维偏离矢量的选值和缩放范围设定。其中，多维偏离矢量选值指的是对不同偏离程度的特征赋予具体的数值，而缩放范围设定则是限制样本随机缩放的上下限。这一过程需要考虑到对象实际物理情况和设计的诊断范围。Comstock等[32]对ASHRAE RP-1043项目中故障的偏离特性进行了实验分析，得出了定性的偏离规律。虽然直接利用这些定性规律实现动态工况故障诊断是十分困难的，但相关规律可以作为本文知识来源。而对于其他情形的诊断过程，亦可以根据对目标系统的相关经验设定偏离矢量选值和缩放范围。本文参考文献[32]对表3 中多维偏离矢量的取值按照偏离程度分别设定，↑/↓取值为2/-2，↑↑/↓↓取值为5/-5，↑↑↑/↓↓↓取值为10/-10，↑↑↑↑/↓↓↓↓取值为20/-20，●取值为0.1，缩放范围为0.7～3.0。

本文研究中发现，单纯利用随机缩放生成的伪数据很难接近真实分布，这主要是由于真实系统具有高度复杂且不确定的特性，使得真实的残差样本具有较高的随机扰动性。针对这一特点，本文提出对生成数据添加随机噪声的策略，使生成数据与真实数据一致性更佳。噪声的添加效果与添加噪声的幅值有密切关系，噪声太小作用无法体现，而噪声太强会破坏数据原有结构。接下来利用实验方式对不同强度噪声添加以及无噪声添加的生成数据进行样本一致性评估。如表5 所示，对添加的标准正态分布噪声进行系数相除，得到不同强度的噪声，同时与不添加噪声的生成数据对比。用于评估的真实数据集包含每类故障2000组样本。

从表5 可以看出，不添加噪声的生成数据与真实数据的MMD 值普遍高于添加噪声的生成数据，表示不添加噪声的生成质量较差。而添加噪声的生成数据MMD 值随添加强度增加呈现先下降后上升趋势，不同故障类别的最小MMD 值对应的噪声强度不同，整体分布于2 倍标准正态分布噪声(/0.5)和20 倍标准正态分布噪声(/0.05)之间。其中，对于正常数据、cf 故障以及rl 故障而言，最小MMD 值出现在更弱的噪声添加策略处，而其他故障的最小MMD 值则对应相对较强的噪声添加策略。深入分析可知，偏离程度越明显的故障类别适于添加更强的噪声，这是因为其自身的偏离较大，更强的噪声也不会对其偏离特性产生较大的影响。而自身偏离较小的故障则对噪声更加敏感，太强的噪声会明显干扰其正常分布。由于MMD 分布的评估并不能完全代表其最终的诊断效果，且在/0.5 和/0.05 添加策略之间的MMD 值差异并不大，因此，最终的噪声添加策略需要进一步结合诊断实验确定。

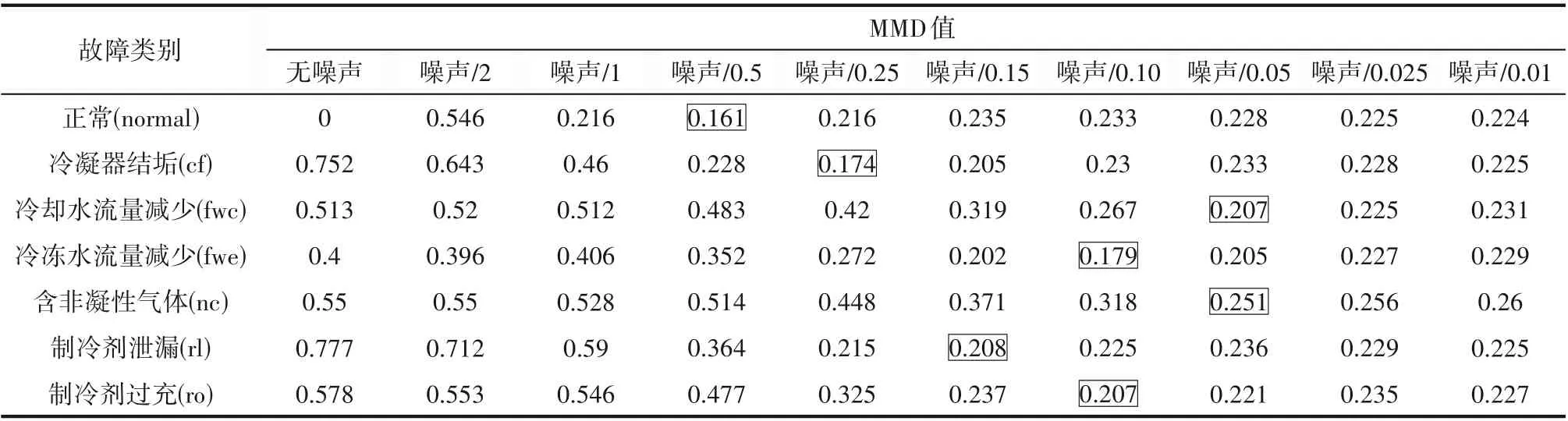
表5 不同策略下生成样本和真实样本的MMD评估Table 5 MMD value of generated samples and real samples under different strategies

4.3 基于知识数据化的故障诊断实验验证

本节对基于知识数据化的诊断方法进行实验验证，验证数据集来自ASHRAE RP-1043，该数据集细节已在3.1 节描述。本节结合4.2 节实验结果，针对MMD 值最小的5 种噪声添加策略和无噪声添加策略进行6组对照实验。诊断模型利用生成的伪数据训练，每种故障类别包含3000 组样本，共计21000组样本。其中，按照3∶1的比例分割训练集和验证集。使用Adam 优化器，批大小为128，训练50轮。完成训练的模型在真实数据集上进行测试，测试集上每类故障2000 组样本，结果如表6 所示。可以看出，添加不同强度噪声的生成策略下诊断精度和MMD 评估呈现较高的相似性。/0.15 的正态分布噪声添加下，模型的诊断精度整体上最高，而/0.15 的噪声强度正好是5 类添加噪声强度中的中间水平，这是一种综合效果的体现。同时可以发现，在不同严重程度数据测试上，越严重的故障越容易被诊断出来，越轻微的故障诊断效果越差。这应该是由于轻微故障表征不明显且被动态工况波动覆盖，导致诊断难度提升。最终表明，使用标准正态分布除0.15的噪声添加下，训练模型的诊断性能最佳，总体正确率可达82.67%，比不添加噪声的诊断精度高11.64%。由于实际应用时，这类渐变热力故障并不需要太高的响应速度，完全可以多次诊断后综合决策，因此这一诊断精度已经较好地满足实际应用需求。

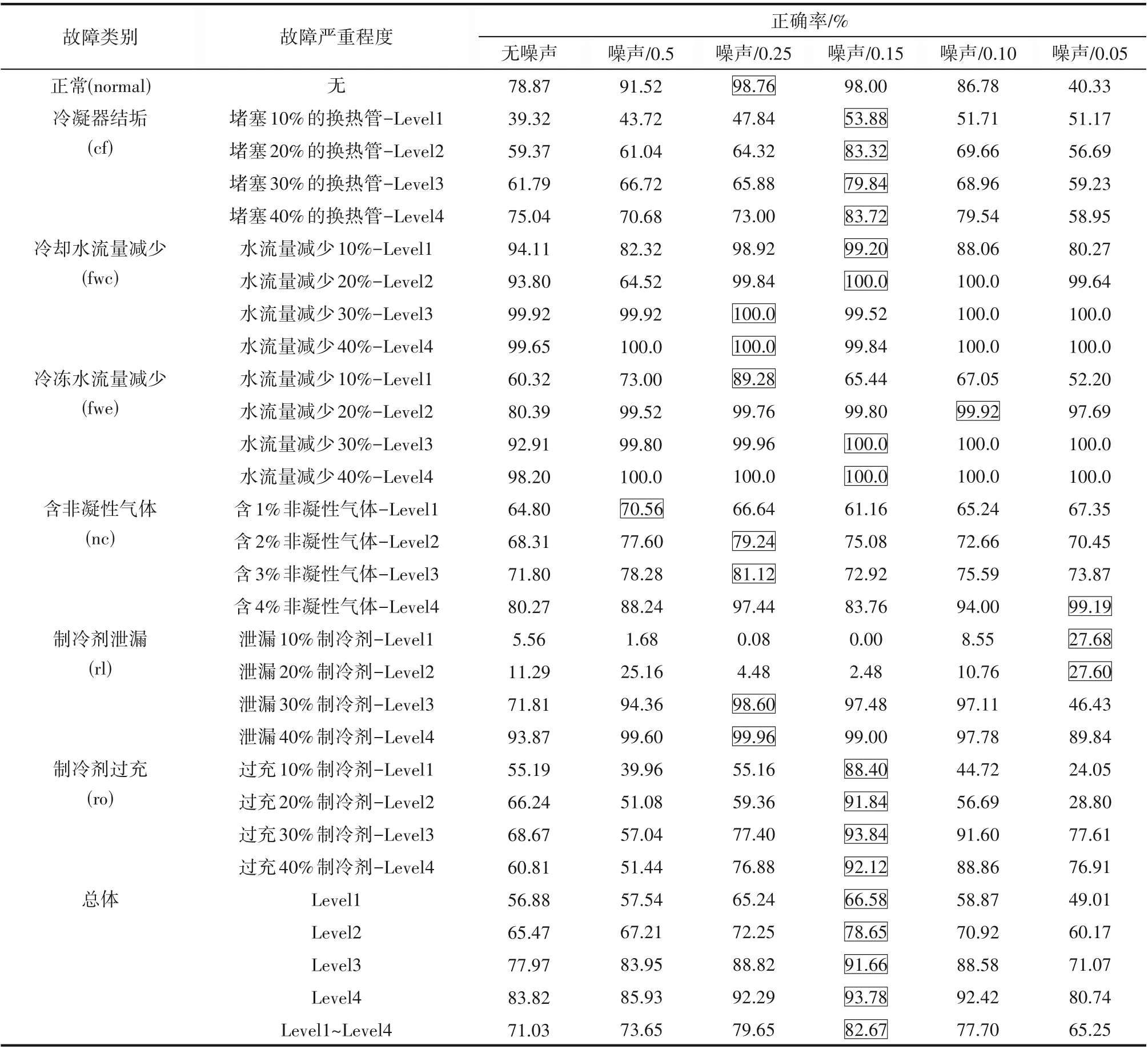
表6 不同生成策略下故障诊断精度对比Table 6 Comparison of fault diagnosis accuracy under different generation strategies

进一步对最优生成策略下卷积网络的全连接层输出进行可视化处理。如图6 所示，分别利用不同严重程度数据进行可视化分析，每种故障200 组样本。可以看出，整体上诊断模型对7 个类别可以较好聚类和分离，但仍存在部分故障的空间分布较近，使得相互误诊率较高。如Level1 中cf 和rl 的空间分布存在部分混叠，rl 和正常数据分布接近，Level2 中rl 和正常数据分布十分接近，造成实际诊断中Level1 的cf 和rl 以及Level2 的rl 故障诊断精度较差。这主要是由于cf和rl故障在轻微状态下隐匿性较高，被热力补偿和动态工况波动所覆盖，导致征兆不明显。这种情形即便是监督学习也很难达到较高的识别精度。

图6 模型全连接层输出特征的可视化Fig.6 Visualization of model fully connected layer

4.4 与监督训练故障诊断方法的对比分析

现阶段智能诊断算法以数据驱动的监督学习模式为主。因此，有必要将监督训练模型与本文方法对比研究。监督学习算法最主要的问题是标记数据获取困难，在无法获取覆盖全局信息的数据集时，模型的适应性存在较大局限。不同严重程度的故障数据分布不同，仅利用单一严重程度数据训练的模型在其他严重程度上会产生精度下降的现象，而实际上可能的严重程度是无限多的，很难获取所有可能严重程度的标记数据。本文针对这一现实问题，对比不同训练数据下的监督学习方法和本文提出方法的诊断精度和自适应性，验证本文方法的优势。

本节设置6 组对比实验，分别是本文提出的知识数据化方法和利用Level1、Level2、Level3、Level4以及Level1～Level4 全部数据作为训练样本的监督学习方法。模型的结构设计和表2 相同，每类故障使用2000 组样本，使用Adam 优化器，批大小为128，训练50轮。

图7 展示了对比结果。从总体精度上来看，利用知识数据化表达的诊断精度为82.7%，这一结果比使用全部数据训练模型的88.2%差，这是很容易理解的，当数据充足时监督学习的效果理应最好，本文重点对比标记数据不充足的情况。从前5组对比实验来看，本文提出的方法仅次于利用Level2 数据集训练的模型，诊断正确率低0.8%，而相比于其他3 组实验的正确率分别高出2.8%、5.9%、20.3%。进一步分析诊断方法在不同严重程度上的适应性。本文提出方法和4组单一严重程度数据训练方法在不同严重程度验证集上的最优诊断正确率分别为：93.8%、83.6%、93.0%、92.8%、95.5%，而最优最差正确率的差值分别为：27.2%、9.1%、19.7%、42.8%、70.1%。综合可以看出，对比4 组监督学习，本文提出的方法在最优诊断和最优最差差值上均处于中间水平，结合该方法完全无须标记数据的特性，表明该方法具有替代监督学习算法的潜力，具有明显优势。

图7 与监督学习的诊断精度对比Fig.7 Comparison of diagnosis accuracy with supervised learning

5 结 论

本文提出一种基于知识数据化表达的制冷空调系统故障诊断方法，通过将故障特征偏离的先验知识转化为数据，解决现有监督学习算法过度依赖标记数据的问题。同时，针对目标系统运行数据，提出一种基于基准模型的数据偏离特性表征方法，将数据的偏离特性提取出来，使之适应于生成数据的形式统一，从而适应于生成数据训练的模型。具体结论如下。

(1)提出一种随机缩放策略用于将知识转化为数据形式并实现信息扩增，其中，提出一种生成数据的噪声添加策略，通过添加不同强度的高斯噪声实现生成分布和真实分布的拉近。实验表明，添加噪声的确会优化生成分布和真实分布的距离，且随着噪声添加强度的增加，分布距离呈现先变小后变大的趋势。同时，噪声添加强度受到故障自身偏离程度的影响，偏离越明显的故障越应添加高强度噪声。

(2)从故障诊断实验验证可知，添加噪声可以明显提升最终诊断精度，且不同噪声强度对诊断的影响不同，其随着噪声添加强度增加，诊断精度呈现先提升后降低的趋势，其结论与MMD 评估结论基本一致。不同噪声添加强度中，添加/0.15 标准正态分布噪声数据后，诊断的整体精度最佳，最优的总体诊断精度可达82.67%，比不添加噪声的诊断精度高11.64%。

(3)与4 组单一严重程度数据监督训练方法对比，本文提出方法仅比使用Level2 数据训练方法的正确率低0.8%，而比其他3 组实验的正确率分别高出2.8%、5.9%、20.3%。在4 个严重程度分别验证实验中可以看出，本文提出方法无论是在最优诊断率还是最优最差的正确率差值上均处于中间水平。结合本文方法完全无须标记数据的特性，其优势明显。

综上，本文提出的知识数据化表达方法较好地解决了监督学习对标记数据的依赖，同时保持了较高的诊断精度，在制冷空调故障诊断领域具有广阔的应用前景。然而，该方法仍然具有一定不足之处。在方法层面上，利用噪声添加虽然一定程度上模拟了真实系统的随机特性，然而热力系统具有时序特点，随机性仍然遵循一定时序规律，因此在随机信息模拟方面如果可以将真实系统时序性考虑进去，则可以使生成分布与真实分布更加接近；在应用层面上，该方法以典型故障偏离知识为基础，因而针对微弱、早期、隐性故障的诊断精度不高，主要是由于这类故障征兆不明显，需要更加复杂的知识作为依据，后续研究中应该更加丰富先验知识的形式，不仅包含定性偏离，还应包含参数间相互映射关系等信息。在知识获取层面上，要研究更加多样的获取方式，包括数值仿真系统、实验系统、理论推导、相似系统知识迁移等多种手段，充分发挥领域专家知识优势，将其作为重要指导依据。如果可以解决上述问题，则该方法的应用场景将会进一步拓宽。