橡胶混凝土单轴受压下的应力应变关系

杨春峰, 闫佳慧, 杨 敏

(1. 沈阳大学 a. 建筑工程学院, b. 辽宁省环境岩土工程重点实验室, 辽宁 沈阳 110044;2. 中节能建设工程设计院有限公司, 四川 成都 610052)

橡胶混凝土是一种新型复合材料,与普通混凝土相比,其延性、耐久性等均有不同程度提高[1-4]。目前,橡胶混凝土的基本力学性能、耐久性能研究较为多见,但针对其应力-应变关系的研究较少。而作为混凝土结构设计中重要依据的应力-应变关系[5-6],对结构有限元分析、抗震设计等发挥着重要的作用。

本文通过试验研究、理论分析、数据拟合等手段,针对橡胶混凝土单轴受压情况下上升段的应力-应变关系展开研究,并拟合出了橡胶混凝土上升段单轴应力-应变关系方程,可供相关研究参考借鉴。

1 试验概况

1.1 试验材料

水泥为普通硅酸盐42.5级水泥,生产厂家为辽宁本溪山水实业有限公司。细集料为天然河砂,含水率为1.2%,表观密度为25 405 kg·m-3,紧密堆积密度为1 615 kg·m-3,松散堆积密度为1 460 kg·m-3,细度模数为2.83;粗集料为天然碎石,公称粒径为5～25 mm连续级配,含水率为2.0%,表观密度为2 780 kg·m-3,紧密堆积密度为1 785 kg·m-3,松散堆积密度为1 610 kg·m-3。橡胶颗粒共3种,分别为胶粒a(粒径为2.36～4.00 mm,表观密度为1 250 kg·m-3,堆积密度为740 kg·m-3);胶粉b(粒径为0.425～0.600 mm,表观密度为980 kg·m-3,堆积密度为337 kg·m-3);胶粉c(粒径为0.18～0.25 mm,表观密度为890 kg·m-3,堆积密度为296 kg·m-3),橡胶颗粒生产厂家为沈阳市宏玉盛橡胶材料厂。预处理试剂为质量分数3%的氢氧化钠溶液。外加剂为UNF-1型萘系高效减水剂,减水效率为15%～20%。

1.2 试验方法

橡胶混凝土设计强度等级为C45,试件采用棱柱体试件,尺寸为150 mm×150 mm×300 mm,试件浇筑振捣并养护24 h后,拆模并放置到标准养护室养护28 d,试件数量共计39个,采用橡胶颗粒等体积取代砂的方式,取代的体积分数分别为5%、10%、15%、20%,试件的橡胶混凝土配合比[7]如表1所示。

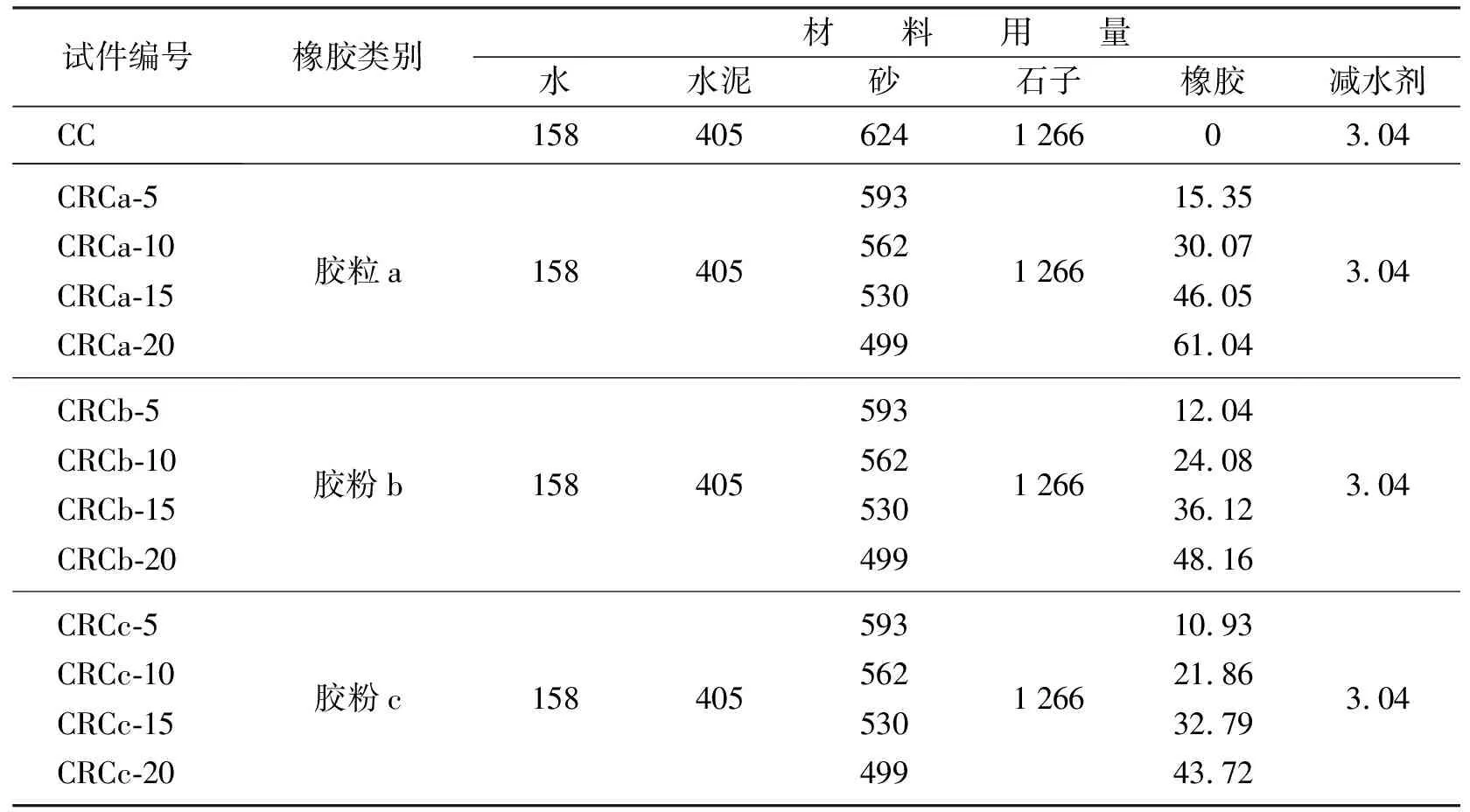
表1 橡胶混凝土配合比Table 1 Mixing ratio table of rubber concret 单位: kg·m-3

试验流程采用标准流程,试件采用双面中心对称布置形式,试件纵向变形采用应变片测量,为了减少误差,首次试验前,动态应变仪先预热15 min,使开始采集的点漂浮控制在最小范围内。试验加载速率为0.3 MPa·s-1。

2 试验结果及分析

2.1 试验数据处理

各组数据处理时,先将各试件的6个应变片的应力-应变试验数据转化为标准形式,把漂浮较大的奇异点排除后,将同组的应力-应变试验数据点投射到相同的坐标系下,选取试验点集中分布于中心区域的试验数据作为该组的试验结果(CRCc-20组采集失败未列出),运用SPSS 19.0统计软件,对各组试验点进行回归分析。为了对比橡胶体积分数对应力-应变的影响,绘出相同橡胶粒径在不同橡胶体积分数下的应力-应变对比曲线,如图1～图3所示。

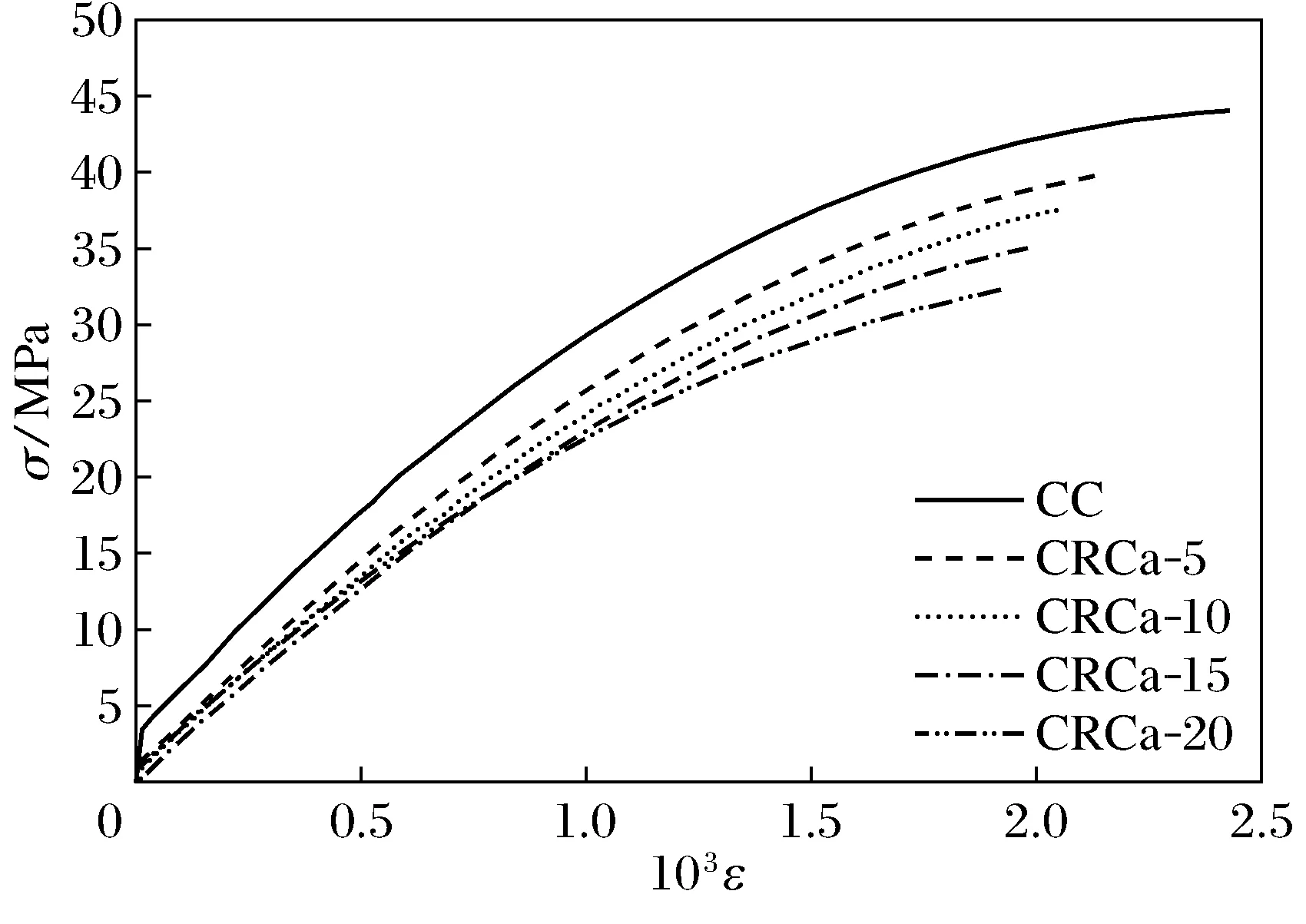
图1 CRCa组橡胶混凝土应力应变曲线Fig.1 Stress-strain of CRCa group

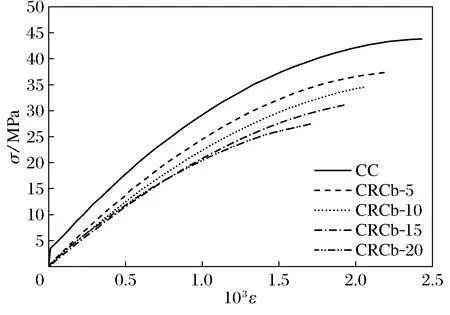
图2 CRCb组橡胶混凝土应力应变曲线Fig.2 Stress-strain of CRCb group

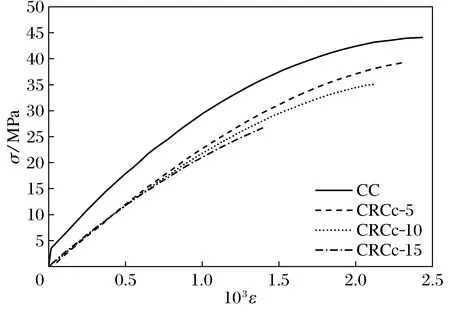
图3 CRCc组橡胶混凝土应力应变曲线Fig.3 Stress-strain of CRCc group

混凝土的峰值应变、弹性模量和割线模量[8]是反映混凝土变形性能的重要指标。根据试验数据,得到各组试件的峰值应变、原点切线弹性模量和割线弹性模量与橡胶体积分数和粒径的关系曲线,如图4～图6所示。

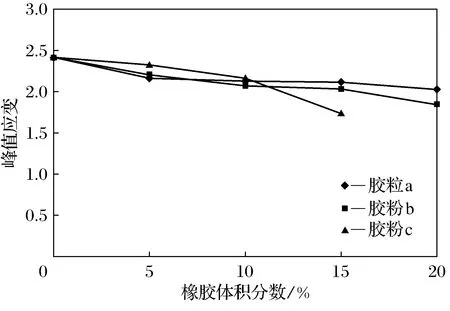
图4 橡胶体积分数峰值应变Fig.4 Amount of rubber-peak strain

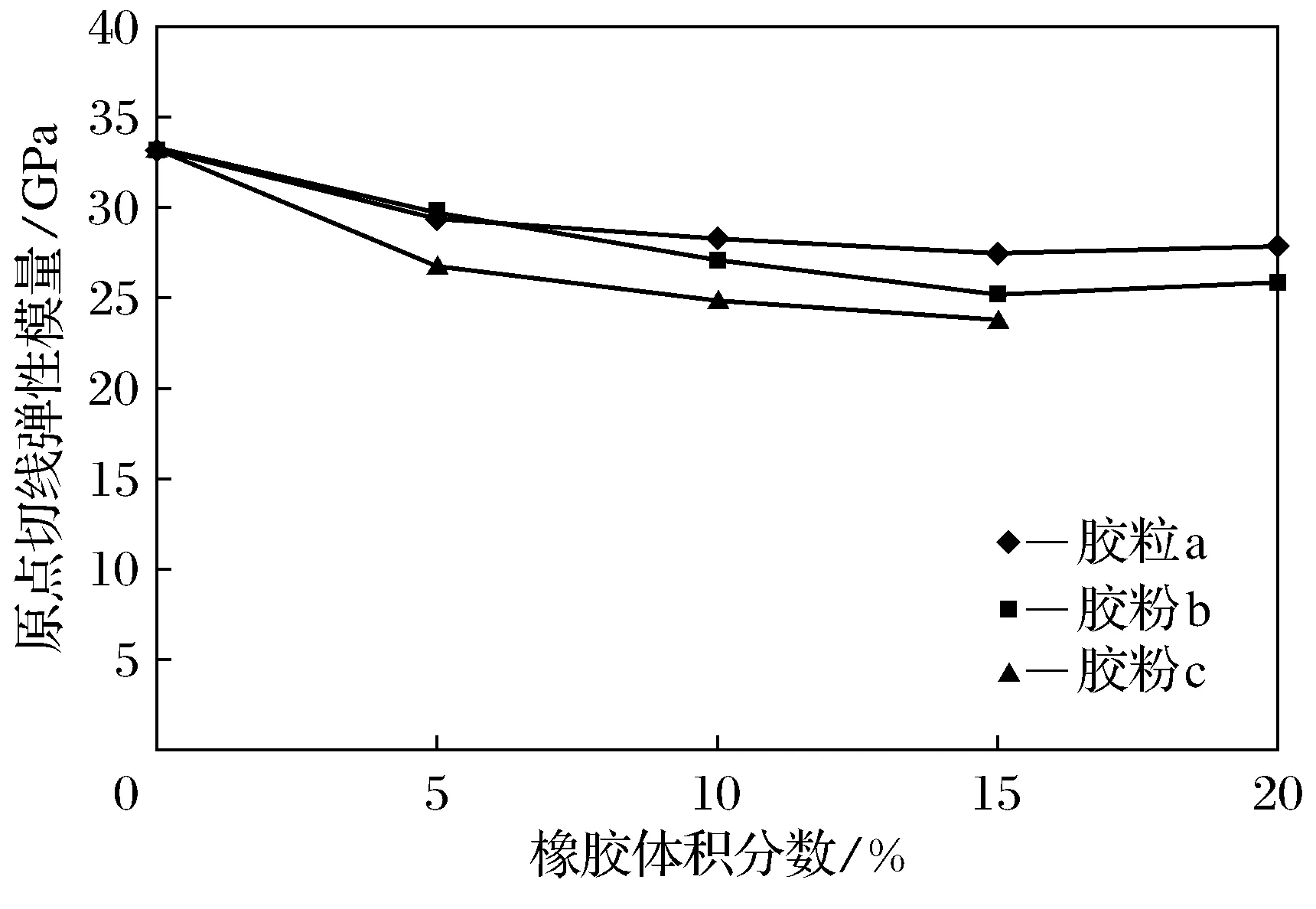
图5 橡胶体积分数原点切线弹性模量

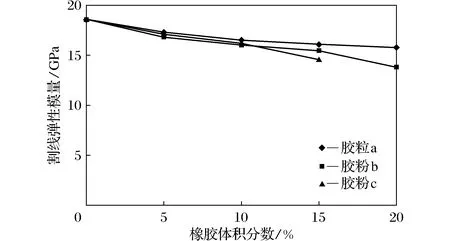
图6 橡胶体积分数割线弹性模量Fig.6 Amount of rubber-sceant modulus of elasticity

2.2 试验结果分析

在试验加载初期和临近峰值荷载[9]时,试验点较分散,故采用数学回归方法对采集数据进行拟合,拟合方程采用三次多项式一般方程,经计算各组试验数据拟合度在0.994～0.999范围内,表明拟合结果较好。

1) 与普通混凝土相比,橡胶混凝土的应力-应变曲线上升更为缓慢。当橡胶粒径相同时,橡胶体积分数越大,曲线上升越平缓;当橡胶体积分数相同时,随橡胶粒径的增大,应力-应变曲线斜率增大。

2) 当橡胶颗粒体积分数在10%以下时,橡胶混凝土的峰值应变和割线弹性模量变化不大;体积分数大于10%时,随橡胶粒径减小,峰值应变和割线弹性模量下降。当橡胶体积分数相同时,橡胶混凝土的原点切线弹性模量基本上随橡胶粒径的减小而减小,但变化规律并不明显。

3 橡胶混凝土上升段应力应变方程

3.1 方程的建立

为便于数据拟合,采用《混凝土结构设计规范》(GB 50010—2010)[10]中给出的混凝土单轴受压应力-应变上升段三次多项式的形式作为拟合基本方程,根据试验数据通过SPSS 19.0得出的橡胶混凝土上升段应力-应变曲线的无量纲拟合方程如表2所示。

表2 橡胶混凝土应力应变曲线的无量纲拟合方程Table 2 Non-fitting equation of stress-strain curves of CRC

表2中的拟合方程的常数项是由试验点的误差引起,其值远小于1,对工程而言可忽略不计,且方程的拟合度R2≈1,表明橡胶混凝土应力-应变曲线的无量纲拟合方程满足三次多项式形式,对上述12组拟合方程中x的一次项、二次项、三次项系数进行回归分析,得到橡胶混凝土应力-应变上升段曲线的无量纲方程基本形式为

y=ax+(2.912-1.976a)x2+(0.907a-1.818)x3。

(1)

式中:a为普通混凝土本构系数;x=ε/εCRC,ε为橡胶混凝土应变,εCRC为与fCRC对应的橡胶混凝土峰值压应变,fCRC为橡胶混凝土的单轴抗压强度;y=σ/fCRC,σ为橡胶混凝土应力。

《混凝土结构设计规范》(GB 50010—2010)中,对于普通混凝土的单轴应力-应变关系推荐采用

y=ax+(3-2a)x2+(a-2)x3。

(2)

其中本构系数为

a=2.4-0.012 5fc。

(3)

式中,fc为混凝土轴心抗压强度。

对比式(1)、式(2)发现,试验数据回归得出的方程(1)与《混凝土结构设计规范》(GB 50010—2010)中规定的混凝土单轴受压应力-应变上升段方程(2)近似相同,因此可以在不考虑分项因素的情况下认为橡胶混凝土应力-应变关系上升段方程满足我国《混凝土结构设计规范》(GB 50010—2010)中所规定的凝土应力-应变关系上升段方程。

本构系数a的试验拟合值及由式(3)得到的计算值如表3所示。

通过表3的相对误差可以看出,试验得出的橡胶混凝土本构系数与普通混凝土本构系数计算结果吻合度不理想,为给出更为精确的橡胶混凝土本构系数,利用MATLAB软件,对试验变量及参数进行多元回归拟合,得到橡胶混凝土本构系数A的拟合方程为

A=aeρ(-2.57+5.35d-1.54d2)。

(4)

式中:A为橡胶混凝土本构系数;ρ为橡胶体积分数;d为橡胶平均粒径,mm。

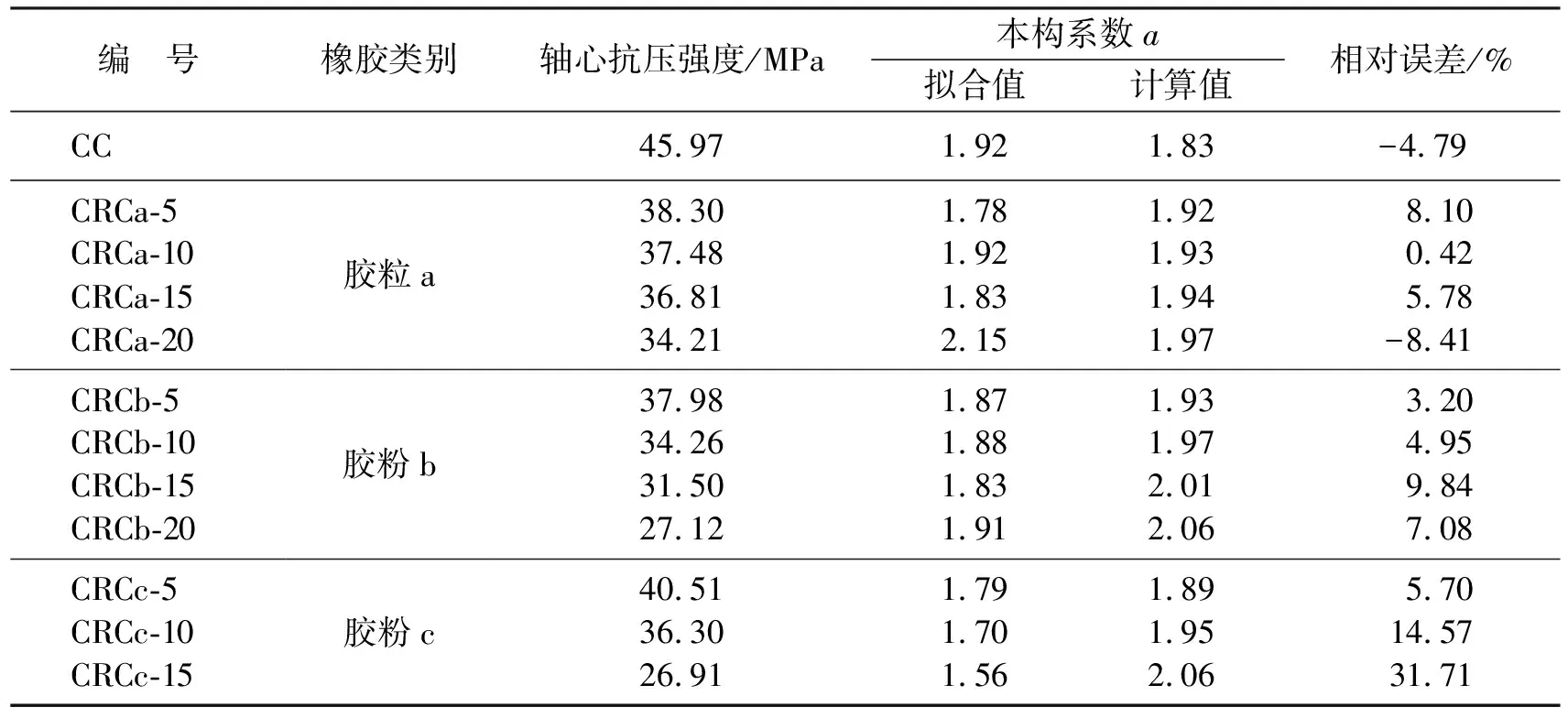
表3 本构系数a的拟合值和计算值Table 3 Fitted and calculated values of constitutive coefficients a

由式(4)计算的橡胶混凝土本构系数A和通过拟合公式得出的橡胶混凝土本构系数如表4所示。

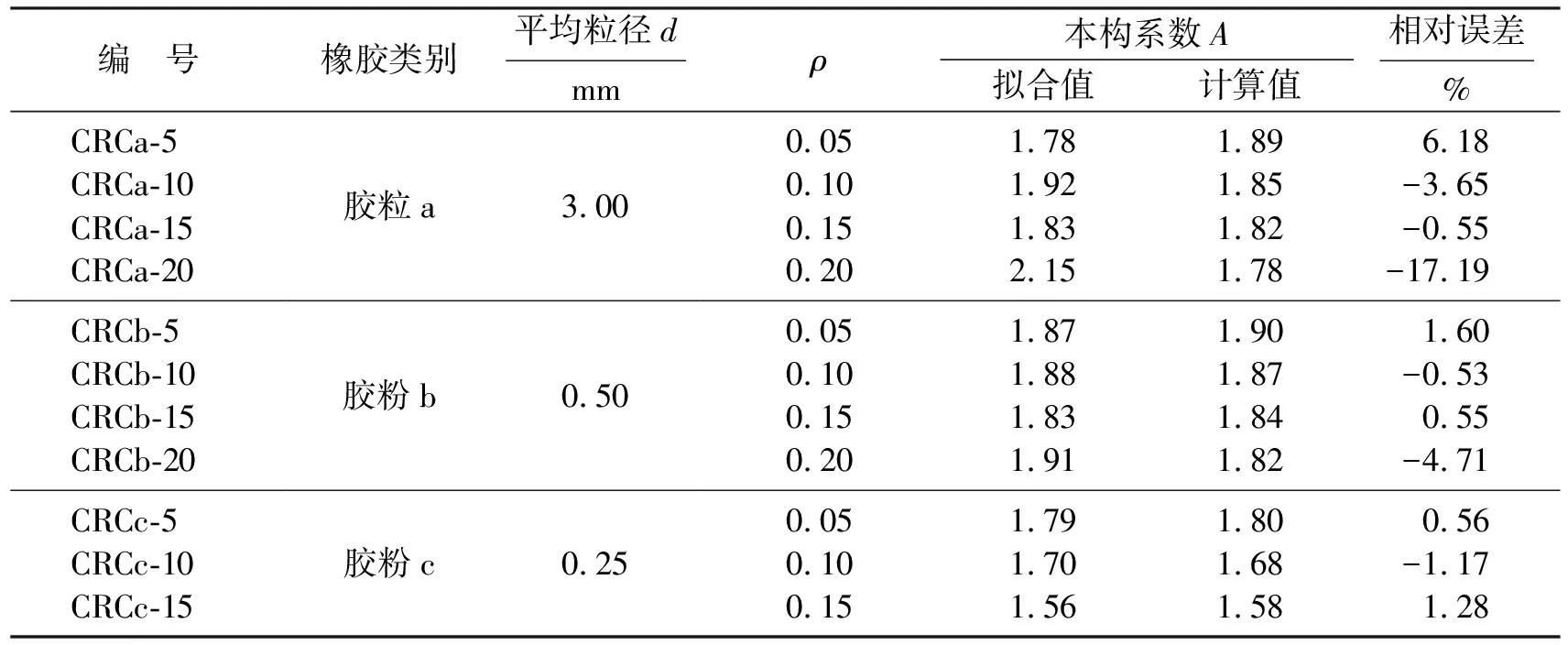
表4 本构系数A的拟合值和计算值Table 4 Fitted and calculated values of constitutive coefficients A

通过表4的相对误差可以看出,橡胶混凝土本构系数A的计算值与拟合值相比,精度上有很大提高,因此将式(4)代入式(1)中,可以得到橡胶混凝土的上升段应力-应变方程,

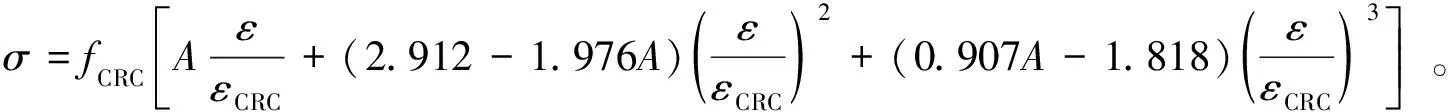
(5)

3.2 验算实例

为了验证推导的橡胶混凝土上升段应力-应变方程的准确性,分别选取掺入体积分数5%胶粒a、胶粉b、胶粉c的橡胶混凝土的试验数据进行验证,计算结果和拟合结果的对比曲线如图7～图9所示。

从图7～图9可以看出,式(5)的计算结果与拟合数据整体吻合较好,表明式(5)给出的橡胶混凝土上升段应力-应变方程是可靠的,可用于理论研究与实际工程设计当中。

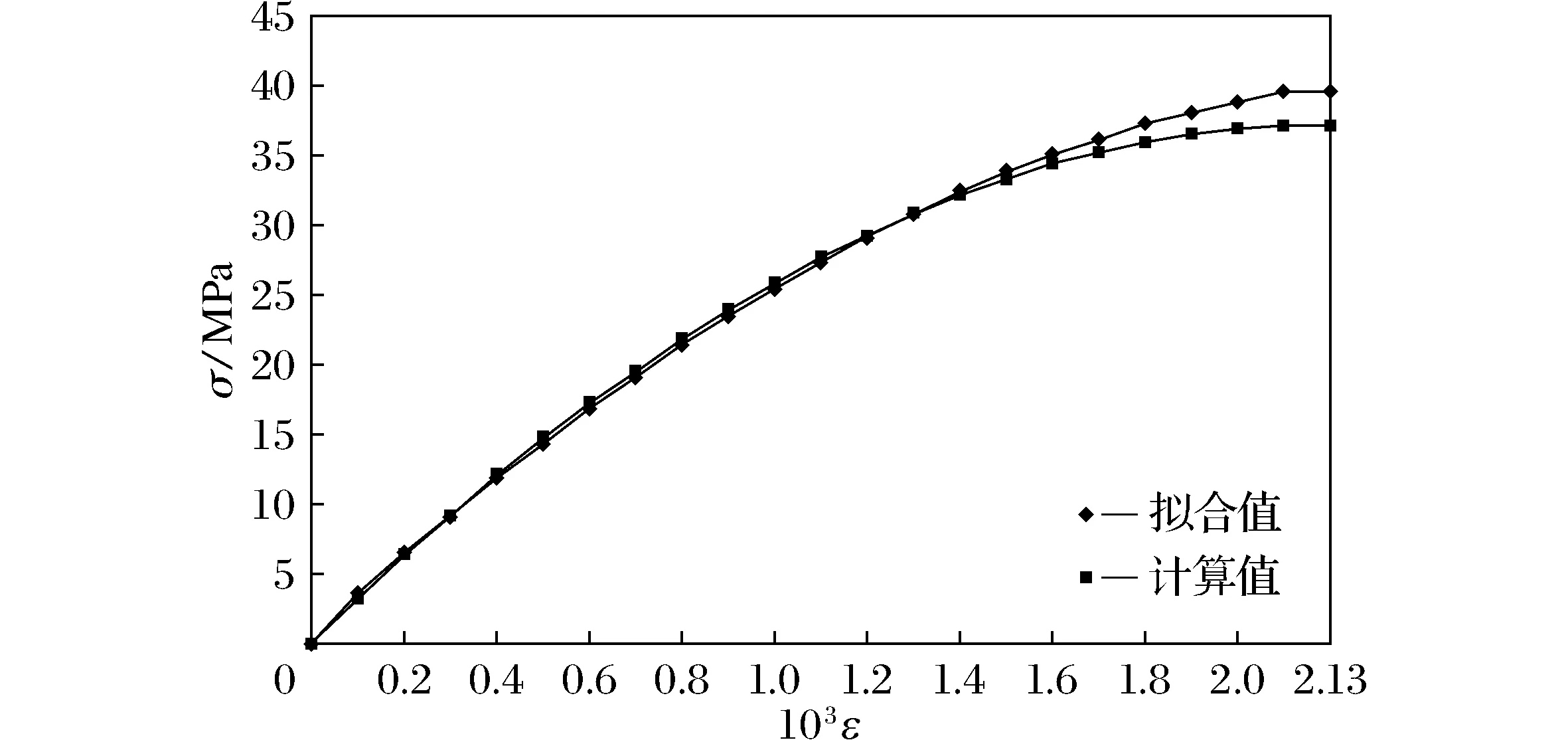
图7 掺入体积分数5%胶粒a的橡胶混凝土应力应变曲线Fig.7 Stress-strain of rubber concrete mix with rubber particles a of 5%

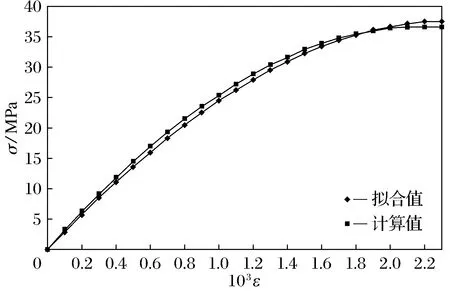
图8 掺入体积分数5%胶粉b的橡胶混凝土应力应变曲线

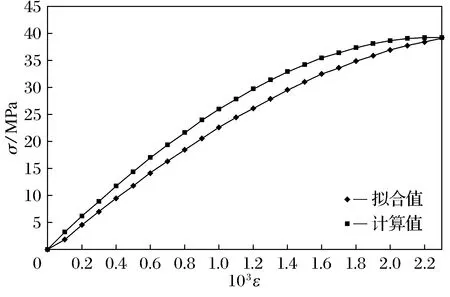
图9 掺入体积分数5%胶粉c的橡胶

4 结 论

1) 整体上,与普通混凝土相比,橡胶混凝土的应力-应变曲线更平缓,橡胶混凝土峰值应变、原点切线弹性模量、割线弹性模量均降低。

2) 在普通混凝土中掺入的橡胶粒径相同时,随着橡胶体积分数的增加,橡胶混凝土应力-应变曲线逐渐平缓,其峰值应变、原点切线弹性模量、割线弹性模量逐渐降低。

3) 在普通混凝土中掺入橡胶的体积分数相同时,加入的橡胶粒径越小,混凝土应力-应变曲线越高;其峰值应变、原点切线弹性模量、割线弹性模量均随橡胶粒径的减小而增大。

4) 对普通混凝土本构系数进行改进,拟合得到了橡胶混凝土单轴受压情况下上升段应力-应变方程,通过试验数据验证了该公式的适用性。