基于自适应形态学的探月雷达噪声压制方法*

张建民，艾伟，张学军，陈路路，杜楚，员建厦，周云，杜丹

（1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.河北省智能化信息感知与处理重点实验室，河北 石家庄 050081；3.陆装驻石家庄地区第一军代室，河北 石家庄 050081）

0 引言

探月雷达是我国嫦娥探月工程中对月表进行实地登录探测的重要手段[1-2]，其原理是通过天线发射的高频电磁波脉冲对隐伏目标体进行探测。其中嫦娥三号探月雷达系统具有两个通道：第一通道中心工作频率为60 MHz，厚度上分辨率为米级，用于浅层月壳结构探测；第二通道中心工作频率为500 MHz，厚度上分辨率小于30 cm，用于探测月壤厚度和结构[3-4]。

然而由于天线耦合、着陆器相关金属构件等工作条件的影响，使得月面下目标的反射信号受到强烈干扰。为抑制杂波噪声干扰，获取更高分辨率的月表层位成像，许多信号处理方法被用于探月雷达信号处理，如反褶积方法[5]、带通滤波[6]、振幅补偿[7]、二维经验模式分解滤波[8]、背景噪声去除方法[9-10]、shearlet 变换[11]等，并取得了良好的处理效果，但这些算法核心构成略显复杂或存在噪声残留问题，为此考虑选取算法构成简单、性能优越、不需频域变换的形态学滤波方法来压制探月雷达信号中的噪声，提高数据的信噪比。

数学形态方法是一种基于积分几何、随机集合论等数学理论发展而来的非线性信号处理方法，算法简单，容易实现，且在图像识别、噪声压制等方面得到了广泛应用。李杰等在2012 年采用数学形态学细化算法对图像边缘进行细化处理，并取得了较好的结果[12]。王大莹等利用形态学方法对激光雷达影像进行建筑物边缘提取，获取了更连续的边缘[13]。石玉敏采用基于数学形态学的船舶图像质量提升方法来获得信噪比更高的船舶图像[14]。胡爱军等研究了开闭、闭开等组合形态算子对于滤波降噪、提高测试信号信噪比的有效性[15]。方文等提出了一种基于数学形态学的密集假目标干扰抑制算法，实现了干扰环境下的目标检测[16]。柴晓飞等提出了一种基于数学形态学的气象杂波抑制方法，较好地消除了气象杂波对雷达系统的影响[17]。

因而，本文将数学形态学优越的信息提取和噪声压制能力应用到探月雷达信号的处理中，以提高探月雷达信号的信噪比和成像分辨率。首先，本文介绍了数学形态学滤波的基本原理；其次，针对探月雷达噪声信号特点，提出一种基于自适应数学形态学的信噪分离方法，该方法能够基于群体的随机搜索全局优化方法，自动选取最佳形态学结构元素的长度和振幅值；最后，利用该形态学滤波对嫦娥三号探月雷达第二通道数据进行逐道处理，结果显示，该方法能够更有效地去除探月雷达信号中的噪声及提高探月雷达成像的分辨率。

1 嫦娥三号探月雷达数据特征

嫦娥三号探月雷达具有CH-2A 和CH-2B 两个通道，其中，第二通道收发天线类型为领结天线，安装在玉兔巡视器底部，离地面约30 cm，工作中心频率为500 MHz，频率范围为250—750 MHz[1,5]，数据采样间隔为0.312 5 ns。搭载探月雷达的玉兔巡视器共行驶了114.8 m，玉兔巡视器路线图如图1 所示，本文选取其中CD 段的Channel-2B 数据进行分析。

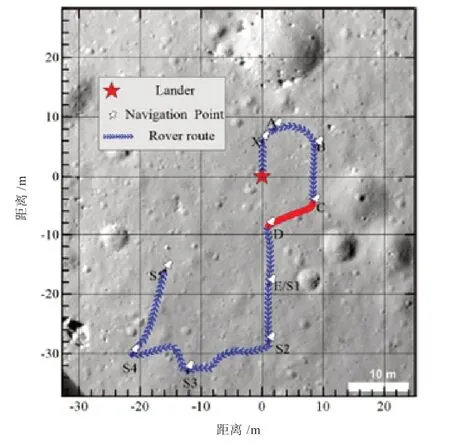
图1 玉兔巡视器路线图

由于数据采集时存在数据重复采集、时间延迟、振幅衰减、直达波干扰等情况[5]，在对探月雷达数据进行进一步分析之前，需要对探月雷达数据进行预处理[11]。预处理后的第二通道CD 段数据如图2所示，可以看出，预处理后的探月雷达信号中具有明显的噪声，以至于信号中的层位结构不能被很好地识别出来，尤其是70 ns 以后的层位结构非常不清晰（图2（a）），严重影响了中深部数据的解释。对预处理结果进行时频分析，可以看出该预处理数据中具有明显的偏离主频信号的低频和高频干扰，主要集中在100 MHz 和1 500 MHz，这些噪声很可能来源于接收天线仪器本身和周围采集环境的共同干扰。为压制其中低频和高频噪声的干扰，本文引入数学形态学滤波方法来抑制噪声。

图2 嫦娥三号探月雷达第二通道数据预处理结果

2 方法原理

2.1 数学形态学滤波基础

数学形态学的基本思想是通过集合论方法来定量地描述目标信号的几何结构，即利用预先定义好的结构元素与信号的几何特征进行局部匹配或修正，同时保留目标信号主要的形状特征，以实现提取有用信息的目的。其中，结构元素是数学形态学的基本要素，具有任意形状和尺寸。

数学形态学的基本运算包括腐蚀、膨胀、开运算和闭运算。设原始信号f(n)为定义在P={0,1,…,N-1}上的离散函数，结构元素g(n)为定义在Q={0,1,…,M-1}上的离散函数，且N＞M，那么f(n)关于g(n) 膨胀和腐蚀运算分别定义为：

式中，符号⊕和Θ 分别表示膨胀和腐蚀运算。形态学上膨胀和腐蚀运算实质上是离散函数在结构元素定义域内的最大值和最小值滤波。其中，膨胀运算表示一个扩张过程，可以填平边界不平滑的凹陷部分；腐蚀运算表示一个收缩的过程，能够剔除边界不平滑的凸起部分。形态学闭、开运算是在膨胀和腐蚀运算基础上组合而来的，分别定义如下：

式中，符号·和◦分别表示形态闭和形态开运算。其中形态学闭运算是对同一结构元素进行先膨胀后腐蚀，开运算是对同一结构元素进行先腐蚀后膨胀。开运算可以剔除信号中的尖峰，抑制正脉冲噪声，闭运算可以补偿谷底，抑制负脉冲的噪声。相比膨胀和腐蚀运算结果，开闭运算可以更好地保留原始信号的主要特征。

2.2 广义数学形态学滤波器的构造

为了更好地滤除目标信号中的正、负脉冲噪声，在闭、开运算的基础上，采用相同的结构元素，可构建出形态学开-闭和形态学闭-开复合滤波器如下：

但由于开运算的收缩性导致开-闭滤波器的输出偏小，闭运算的扩张性导致闭-开滤波器的输出偏大，所以为了取得较好的滤波效果，通过二者的平均值，构造出新的滤波器如下：

式中，Mgf表示该形态学滤波器在结构元素为g时对信号f的滤波结果。

形态滤波的质量不仅取决于所选择的形态变换，而且和选取的结构元素也有较大的关系。结构元素在形态学运算中的作用类似于一般信号处理时的滤波窗口或参考模板，其形状和尺寸都对形态学的运算结果产生影响。常见的结构元素形状有直线形、正方形、抛物线形、三角形、正弦形等。本文选择的结构元素形状为抛物线形，定义如下：

从式(8) 可以看出，抛物线形结构元素结构简单，其中参数A和L控制结构元素的幅值和长度。一般来讲，利用大尺寸结构元素的形态滤波器可以提取目标信号的大致轮廓信息；小尺寸结构元素的形态滤波器可以提取目标信号中相对细节的信息。然而，对于探月雷信号既有低频噪声又含高频噪声的特点，采用单一结构元素的形态滤波器类似于低通滤波器，不能呈现出信号中间某一段频率范围的信息。为了增强形态学滤波器的适用性，提取信号中有用的信息，通过如下思路对信号进行形态学处理：

假设目标信号f被结构元素为gu的形态学滤波器处理得fu，那么根据式(7)可有：

如果信号fu被尺寸大于gu结构元素gv的形态滤波器处理，可获得fuv和RMMF，表示如下：

其中，RMMF代表提取信号中某一频段范围的信息。

2.3 形态学结构元素的全局优化方法

利用提出的数学形态学滤波方法获取输入信号中的有用频段信息时，形态学结构元素A和L的选取对处理结果有较大影响，因此如何确定结构元素尺寸的参数，是应用数学形态学滤波方法实现有效压制信号中噪声的关键。本文利用基于群体的随机搜索全局优化方法求解形态学滤波方法的最优A和L值，以构建自适应形态学滤波方法。

粒子群随机搜索全局优化方法具有收敛速度快、精度高、操作性强等优点，在许多优化问题中得到成功应用[18]。粒子群优化算法首先在给定的空间内随机对粒子群进行初始化，并且每个粒子都有一个由适应度函数决定的适应值。每个粒子根据个体经验和邻居经验来决定飞行的距离和方向，从而粒子群就随当前的个体极值和全局极值，一代代在解空间中搜索出最优解。

设在一个D维空间中，由M个粒子组成的种群为X=(X1,X2,...,XM)，第i个粒子的位置为。将Xi代入适应度函数中计算出适应度值及粒子位置。第i个粒子的速度为，其中粒子i的个体极值为,种群的全局极值为。粒子通过两个极值迭代更新自身的速度和位置，如下：

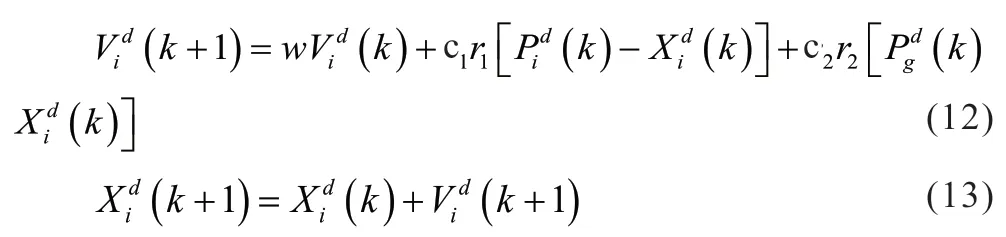
式中，i=1,2,…,M，d=1,2,…,D，M和D分别为种群的大小和待优化问题的维数；w是惯性权重；k是当前迭代次数；c1、c2是加速常数；r1、r2是随机数，范围为(0,1)。

本文采用包络熵Ep作为适应度函数[19]，来评价粒子位置的好坏程度。其原因为：包络熵Ep可定量表示原始信号的稀疏性，Ep值越大，则信号稀疏性越弱，即含有越多噪声；反之，Ep值越小，则信号稀疏性越强，即含有噪声越少，当噪声最少时，粒子所处位置最好，即对应结构元素的A和L最优。信号S 通过Hilbert 解调后，所得包络信号sig(i)(i=1,2,…,N)的包络熵Ep计算公式如下：

式中，pi为包络信号sig(i)归一化形式。

形态学滤波方法最佳结构元素振幅和长度的优化搜索过程如下：

①对粒子群优化方法参数进行初始设定，将相应的包络熵Ep确定为适应度函数；

②随机产生粒子种群中一些粒子的位置及其移动速度；

③对信号在不同位置下进行形态学滤波处理，计算每个粒子位置相应的Ep值；

④对比Ep值大小，利用式(12)、(13)更新粒子的移动速度和位置；

⑤循环步骤③～④，当迭代次数达到阈值后结束循环，并输出最佳粒子位置。

3 实测数据测试与性能分析

为获得更加清晰的探月雷达成像分辨率，利用以上提出的自适应形态学滤波方法，对图2（a）信号中噪声部分进行压制，提取中间频率范围有用信息。其中，为加快运算速度以及保证结构元素幅值作用的一致性，采用结构元素长度不同、幅值相同的两个结构元素，来构造式(11)中的形态学滤波器。对两个结构元素尺寸自动寻优的粒子群算法参数设置如表1 所示，寻优过程中极小包络熵值随种群进化代数的变化如图3 所示，极小包络熵最小时，完成优化过程，对应的两个结构元素的长度分别为5 和6，幅值为3。

表1 粒子群算法各项参数

图3 极小包络熵值随种群进化代数的变化

利用带通滤波、EMD（Empirical Mode Decomposition，经验模态分解）方法以及自适应形态学滤波方法，分别对预处理后的探月雷达数据进行处理，结果如图4、图5、图6 所示。利用带通滤波处理后的雷达成像结果中有明显的条带状噪声以及70 ns 后的层位结构难以识别（图4（a）），时频谱特征显示，带通滤波能够很好地去除信号中的高频噪声以及部分低频噪声，但80 ns 后仍残留较多的低频噪声（图4（b））。EMD 方法处理后的结果显示，EMD 方法虽然能够较好地去除信号中的低频和高频干扰，但雷达数据成像结果中仍存在比较明显的条带状噪声（图5），影响数据的解释和分析。图6 显示了利用自适应形态学方法处理的结果，可以看出自适应形态学方法相比带通滤波以及EMD方法具有更强的噪声压制能力，能够很好地去除信号中低频和高频噪声，保留预处理后数据中的有用信息，使反射的回波信号更加连续清晰，同相轴特征明显。同时，利用式(15)计算了嫦娥三号探月雷达预处理数据以及利用带通滤波、EMD 方法和自适应形态学方法处理结果的包络熵，结果分别为6.041 0、6.036 7、6.014 5、5.873 3，可以看出，利用自适应形态学滤波方法获得的包络熵结果相比带通滤波和EMD 方法获得的包络熵结果更小，即剩余噪声越少，这进一步说明了自适应形态学滤波具备更强的噪声压制能力。

图4 图2（a）数据经带通滤波处理后的结果

图5 图2（a）数据经EMD方法处理后的结果

图6 图2（a）数据经自适应形态学方法处理后的结果

4 结束语

本文提出了一种基于自适应形态学的探月雷达噪声压制方法，该方法利用两个不同尺寸的抛物线形结构元素，构造出能够提取信号中间尺度范围的形态学滤波器，并将包络熵作为目标函数，通过粒子群随机搜索全局优化方法对形态学结构元素的幅值和长度进行优选。通过对嫦娥三号探月雷达第二通道数据测试结果表明，相比常用带通滤波方法、EMD 方法，该方法具有更强的噪声压制能力，能够更有效地去除探月雷达信号中的干扰信息，大幅度提高了雷达信号成像的分辨率，从而为月表结构的合理划分提供了较好的支撑依据。同时，本文提出的方法可为嫦娥四号、嫦娥五号探月雷达数据的处理和解析提供技术方法参考。