DCF模型在不同利率环境下的适用性研究

陈镛屺

（共青城汇诚达私募基金管理有限公司）

一、引言

（一）研究背景及意义

2016年10月13日，财务分析公司Sanford Berns- tein在彭博社上发表了一篇题为“低利率使股票估值观念变得过时—DCF估值方式和低利率无法共存”的文章，在该文中分析师Inigo Fraser-Jenkins指出：“低利率成为新常态意味着，公司近期估计的财务业绩对净现值的影响权重将越来越少；同时，随着公司长期业绩的不断增长，其重要性将不断提高；然而，未来利率和现金流却拥有更高的不确定性。”

自21世纪以来，全球大部分主要经济体的基准利率呈现走低趋势。图1呈现了中美英日欧五大主要经济体的10年期国债收益率，可以看出，除中国外，美英日欧的10年期国债收益率在近5年均处于1.5%以下，日欧甚至出现了负利率的情况。进入2022年，虽然美国加息缩表步伐加快，但美债仍处在历史整体较低利率水平，可以预期的是，在未来较长一段时间内，全球大概率仍将维持低利率/较低利率的状态。

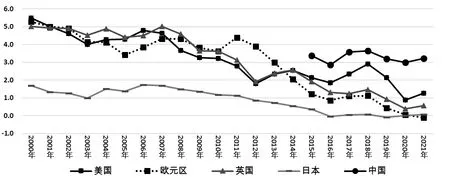
图1 2000—2021年中美英日欧10年期国债收益率（%）

低利率的货币环境促使经济蓬勃发展，市场经济下企业的增资扩股、并购、重组等交易类活动愈发频繁，这些活动都需要对企业价值进行评估；现金流折现估值模型（DCF模型）作为企业估值的经典方法之一，在企业价值评估的金融实践中被广泛应用。此外，自20世纪初模型被提出后，国内外学术界就DCF模型进行了大量的讨论和研究，极大地丰富了该模型的内涵和外延，但少有研究与近十年低利率环境相结合。

DCF在理论研究中的大量讨论和实践应用中的广泛使用，面对历史上少有的长期低利率背景，其方向上的准确性值得重新审视。基于此，本文首先选定恰当的DCF模型，再通过一定的假设来计算各年现金流在PV中所占的比重，探讨长期低利率情况下DCF模型对公司估值精确性的影响。

（二）国内外研究现状

对于DCF模型的适用性，国内外大多数文献主要从以下两个方面展开分析。一是结合具体案例，讨论DCF对于某个特定行业的适用性。如王竞达、刘中山在“现金流折现模型在医药行业公司价值评估中的适用性研究”中通过实证方法指出“自由现金流折现模型适用于我国医药行业上市公司的价值评估”；杨洁妮在“基于修正现金流量折现模型下新能源汽车企业价值评估”中，通过评判新能源汽车行业的特性，认为收益法优于成本法，并引入加速增长率概念对模型进行修正，对新能源汽车蔚来企业进行价值评估。二是通过横向对比其他企业估值方法，讨论DCF模型的适用性。如田增润在“企业估值方法比较分析”中指出，DCF适合“那些能准确测算未来现金流量及贴现率的企业，对于处在财务困境时期的企业、正在进行重组并购的企业、有专利权或产品选择权的公司不适用”。

无论是对某个具体行业的适用性，还是对企业经营状态的适用性，均是针对DCF估值模型中的分子进行的讨论和优化；而对于分母适用性的研究仍有发展空间。喻少华在“精确的错误：DCF估值法的谬误”中指出，“DCF估值模型对折现率相当敏感，折现率百分之一的轻微变动能导致结果百分之几十的剧烈变动，对估值结果影响巨大”。

学者喻少华和分析师Inigo Fraser-Jenkins均指出了折现率对DCF估值结果的巨大影响，本文在此基础上，尝试通过具体量化的方式，进一步探究该影响。

二、DCF模型的选用和假定

（一）模型选用

一般而言，企业估值方法包括现金流量折现法（DCF）、相对估值法和期权定价模型法，其中DCF的基本方程为：

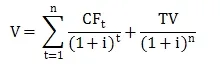
其中，V代表目标企业价值；CF代表第t年的现金流；TV代表价值终值；n代表预测年限；i代表贴现率（机会成本）。代表资产持有人要求的收益率，表示投资者如果投资其他资产所获得的平均收益率。在此，“平均值”可以理解为市场的平均值、某个行业的平均值或某类企业的平均值，该利率取决于投资者的主观意愿，但高于无风险利率。

具体来说，根据现金流量的差异，DCF模型可以分为四种类型。

1.红利折现下的DCF模型

现金流在持有期间分为股息和股票的利差，通过预测每股收益和股息支付率来获得DIV，之后以一定的k值得到每股的PV：

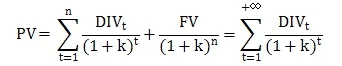
其中，PV代表目标企业每股现价；DIV代表企业第t年的分红；FV代表t年末的股价；

k代表股本成本；n代表持股期限。

2.股权自由现金流下的DCF模型

FCFE是股权自由现金流，指偿还债务和再投资后的剩余现金流量，对应净现值计算方式为：

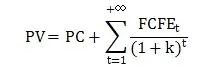
其中，PV代表权益现值；PC代表现有资本；FCFE代表第t年的股权自由现金流量，FCFE=净利润+折旧+摊销+净债务增加-净营运资本增加-资本性支出；k代表权益资本成本。

3.企业自由现金流下的DCF模型

FCFF是企业自由现金流，指再投资后的剩余现金流量，对应净现值计算方式为：

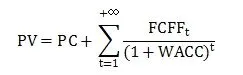
其中，PV代表公司现值；PC代表现有资本；FCFF代表第t年的企业自由现金流量，FCFF =税后净利润+利息费用+非现金支出-营运资本净增值-资本性支出；WACC代表加权平均资本成本。

4.经济增加值（EVA）下的DCF模型

经济增加值（EVA）从货币角度判断投资回报与资本成本之间的差异，这表明投资者将仅从运营成本中受益，而资本成本得到补偿。

其中，NOPAT代表税后净营运资本；CAP代表资本性投资金额；WACC代表加权平均资本成本。

比较DCF基本模型及四个衍生模型，其区别包括期限处理、现金流定义、折现率定义三方面。

第一，期限。对于现金流量，其产生越早，带来的不确定性越少，因此，本文将“未来”划分为两部分，第一部分是前十年，逐年计算每年的影响力，第二部分是十年后，在模型中将其视作永续增长。

第二，现金流的定义。基本方程式中未对该概念进行细化，而在其他四个特定公式中现金流量具有不同的含义，考虑到：本文核心在于研究利率环境对DCF模型的影响，利率环境与期限时长和利率变化有关，而各期现金流作为分子，其变动不影响本文研究推算过程和结果；在实际中，现金流量是特定的，投资者可以将现金流量替换为任何既定的数值。因此，分子现金流量的选取不对本文研究构成影响。

第三，折现率。在五组DCF公式中，i表示折现率或机会，k表示资本成本，WACC表示加权平均资本成本。考虑到WACC是最具体、最详细的变量，且在行业实操中多使用WACC进行估值，本文后续使用WACC作为折现率。

综上，本文使用如下公式：

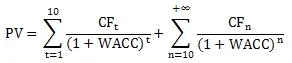
（二）公司及利率假定

1.未来现金流CF

假定初始值CF为1，并使用公司增长率来确认接下来几年的现金流量。此外，假设四家公司代表四种不同的典型公司类型，如表1所示。A：普通成长中的公司。该类公司增长较快，几年后可能会出现边际效用递减的现象，并最终保持稳定增长。

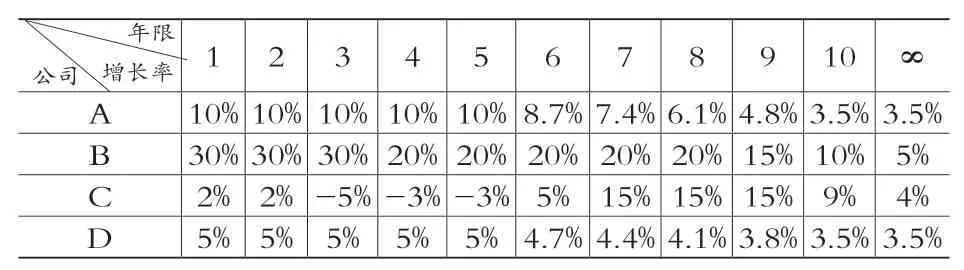
表1 公司增长率假设

B：有一定壁垒的成长公司。由于技术、市场、资质等壁垒，这类公司在前期会有爆发式的增长，根据产业周期理论，这种高速的增长可以维持较长的时间。因此，我们假定B公司前三年的年平均增长为30%，之后的5年中每年有20%的增长，随着公司及行业的成熟最后逐渐衰减至5%。

C：经营困难而进行内部改革转型的公司。公司在前几年的增长极为缓慢，甚至出现了负增长，渡过转型的困难期后经营状况逐步好转，最后维持在5%的稳定增长。

D：成熟行业龙头企业。因上下游市场的成熟稳定，企业难有明显的业绩波动。

2. WACC

假定七个不同的利率环境，分别为20%、15%、10%、7.5%、5%、3%和1%。

三、DCF模型在不同利率下的适用性

（一）结果计算

分别计算4家公司在不同WACC利率环境下，未来各年累计现金流（CF）的现值在总PV中所占的比重，如表2所示。

表2 4家公司测算结果

（二）主要结论

重点观察前三年和前五年在整个现值中的权重或影响力，这样做的原因如下：

第一，就预测本身而言，DCF模型对参数有很强的依赖性。实操中设定的时间越近，参数越精确，DCF模型的权重或影响就越大。相反，时间越远，参数获得的不确定性将越大，参数将具有越低的效率。因此，如果大部分PV来自3年或5年后，由于巨大的不确定性带来的现金流等参数的估算误差，这部分PV将具有极大的不确定性。

第二，从投资者的角度来讲，投资者通常期望在相对较短的时间内获得投资回报。对于大部分投资者，2～5年应该是出现投资回报的第一阶段，这一阶段对他们来说非常重要。

第三，从公司的角度来讲，考虑到各种定期债务、薪酬奖金、再投资和再生产、股东回报及其他压力，近3～5年内带来的价值比五年或十年后带来的价值更重要。基于此，距离当下较近的折现现金流比较远时期的现金流具有更重要的意义。

因此，由于前三年和前五年带来的现金流具有较高的确定性且大部分投资者更为重视，本文统计四家公司前三年及前五年现金流对现值的贡献比例，如表3所示。

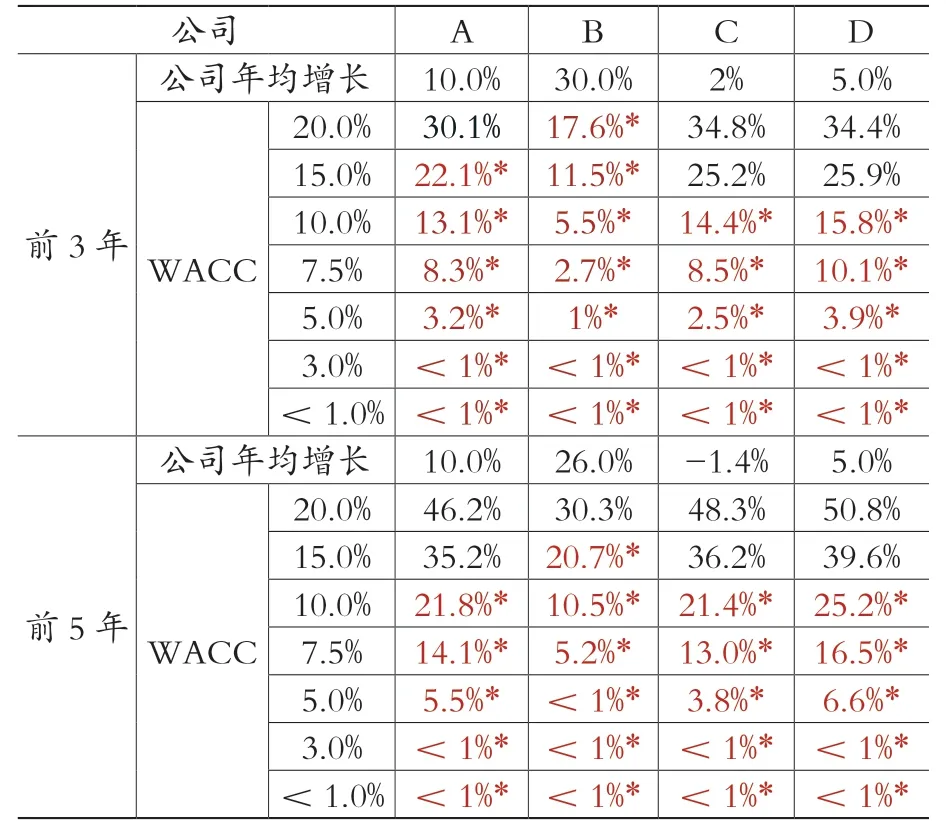
表3 不同利率环境下各类公司使用DCF模型折现后前3/5年现金流在总折现值中的占比

对于前三年的贡献比例，如果其低于25%，那么三年后现金流的贡献比例就将超过75%，也就意味着预估的现值中至少75%具有很大的不确定性。虽然本文未对这种不确定性进行量化，但可以肯定的是，对公司未来现金流折现的估计金额中超过75%的部分具有很大的不确定性，无论是从客观的学术角度，还是主观的投资人或者公司角度，都难以接受如此大的风险。

同样，如果前五年的贡献比例低于35%，那么预估的现值中超过65%都具有极大的不确定性，也是“不应该被允许的”。

表3中将不符合上述条件的比值标明*，可以看出，和A公司相比，在相同的折现率WACC水平下，B公司前三年或前五年现金流带来的现值，其比重更低。在高利率的情况下，C公司的前几年现金流折现的比重略高于A、B两家公司，但低利率的情况下三者之间并无明显差别，D公司的情况和C公司相似。

整体来看，只有在WACC维持在一个相当高的折现水平时，部分公司才适用DCF，也就是说，在低利率或是较低利率的情况下，使用DCF模型进行折现对现值进行估算，得到的估算值当中有超过75%/65%的比例具有相当大的不确定性，这样的情况“不应该被允许”，这意味着使用DCF模型对企业进行价值评估失去了确定性。