基于CA模型的大型会议室疏散空间特性模拟研究
赵菁洁,尹 贺,刘朝峰
(1.秦皇岛市建设工程抗震防灾服务中心,河北 秦皇岛 066000;2.河北工业大学 土木与交通学院,天津 300401;3.中国地震局工程力学研究所地震工程与工程振动重点实验室,北京 100124)
随着人们对各种形式会议交流需求的增加,高校、写字楼、酒店等创建了各种形式的大型会议室,这些会议室属于人员密集的公共场所,其空间布局复杂,特定时间人员集聚众多,如图1所示,同时人员行为主观性较大,且易受空间环境影响,在疏散过程中容易出现恐慌、推搡等心理或行为,进而可能会导致踩踏等事故的发生[1-2]。大型会议室空间布局的合理性与消防安全措施的科学性对人员应急安全疏散至关重要。一旦发生紧急事件,如果人员疏散不及时,可能会造成重大的人员伤亡和财产损失。因此,有必要开展大型会议室的人员疏散过程的仿真模拟,解析大型会议室的疏散空间特性,提出更为科学合理的疏散空间优化方案。

图1 大型会议室室内空间布局示意图
传统的室内应急疏散研究多通过现场人员疏散实验等手段获取数据,建立数学物理模型进行分析[3-4],但建立考虑人员心理行为和空间环境的数学物理模型难度较大。随着计算机仿真技术的快速发展,越来越多的研究采用仿真模拟技术进行室内人员疏散分析[5-7],基于元胞自动机的仿真技术是重要的研究手段之一,被广泛地应用于模拟人员应急疏散过程。翟越等[8]利用元胞自动机进行有无障碍物影响的室内人员疏散模拟,提出了改进元胞自动机人员出口选择算法。陈长坤等[9]采用元胞自动机建立了恐慌状态下行人决策修正模型,研究了恐慌情绪对人群疏散行为的影响规律。宋英华等[10]建立了考虑环境熟悉度及引导作用的行人疏散元胞自动机模型,分析了环境熟悉程度及引导作用对人群疏散的影响。ZHENG等[11]建立了考虑火灾及烟气蔓延的人员疏散模型,分析了火灾及烟气对人员疏散过程的影响规律。金泽人等[12]考虑火灾导致的恐慌对移动方向的影响,对已有场强模型进行修正。
综上所述,大多数研究集中在室内人员疏散模型建立上,考虑人员心理、行为及突发事件影响下元胞自动机模型的修正或算法优化较多,较少研究考虑人员行为的大型会议室等大空间、人员密集场所的疏散空间优化。因此,笔者考虑人员行为和空间环境,建立考虑障碍的大型会议室人员疏散元胞自动机模型,研究大型会议室疏散空间特性对人员疏散行为的影响,提出大型会议室疏散空间的优化方案。
1 人员行为疏散CA模型
根据某高校大型会议室空间尺寸和人员在紧急情况下行为特点,采用Moore型邻域的元胞自动机方法[13-14]模拟大型会议室紧急事件下人员疏散行为及疏散空间特性。Moore型元胞自动机模型如图2所示,1个元胞只能容纳1个行人,行人可选择向其周边8个相邻的、空闲的某一元胞移动,也可停留在原来元胞位置。
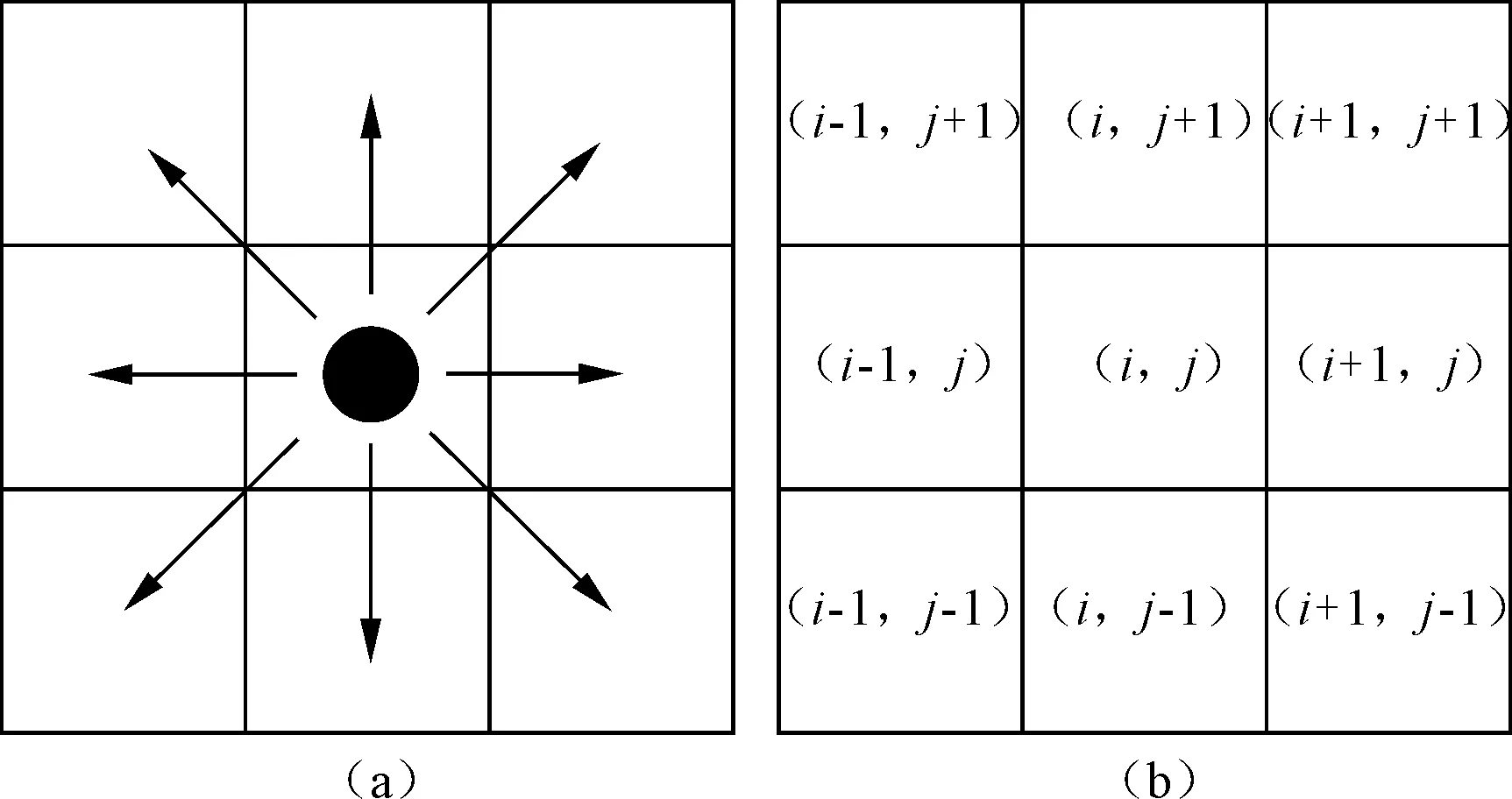
图2 Moore型邻域的元胞自动机模型示意图
将大型会议室疏散空间映射到二维离散元胞空间平面中,选定的大型会议室疏散空间平面尺寸为40.4 m×40.4 m,以0.4 m×0.4 m大小将其划分为101×101个网格,每个网格为1个元胞,其坐标为(i,j),每个元胞存在两种状态:①元胞被占据(如行人或桌椅等);②元胞空闲。用障碍物占据系统边界元胞形成会议室围墙(墙宽占据1个元胞),在墙体上设置空元胞作为会议室的安全出口;考虑大型会议室建筑设计规范要求,其安全出口不应少于2个,因此在疏散空间内设置初始安全出口数量E=2,其中A出口位于左侧墙体且距顶部第10个元胞处,B出口位于下侧墙体且距左侧第10个元胞处;安全出口初始宽度D=4。桌椅初始布局为40排、6列(黑色区域为桌椅),课桌长度占据6个元胞。每列桌椅之间的空间为“列过道”,可根据桌子长度、行列数自动设置宽度。将每排桌子之间的过道称为“行过道”。规定行人每个时间步(用T表示,单位为Step,简写s)移动1个元胞,即移动速度为1步长,行走为0.4 m。一般情况下行人平均速度为1.2 m/s,紧急情况下1.5 m/s。人员初始位置均匀分布在各排座椅上,人员初始密度ρ可变化,初始工况可设置为0.5。
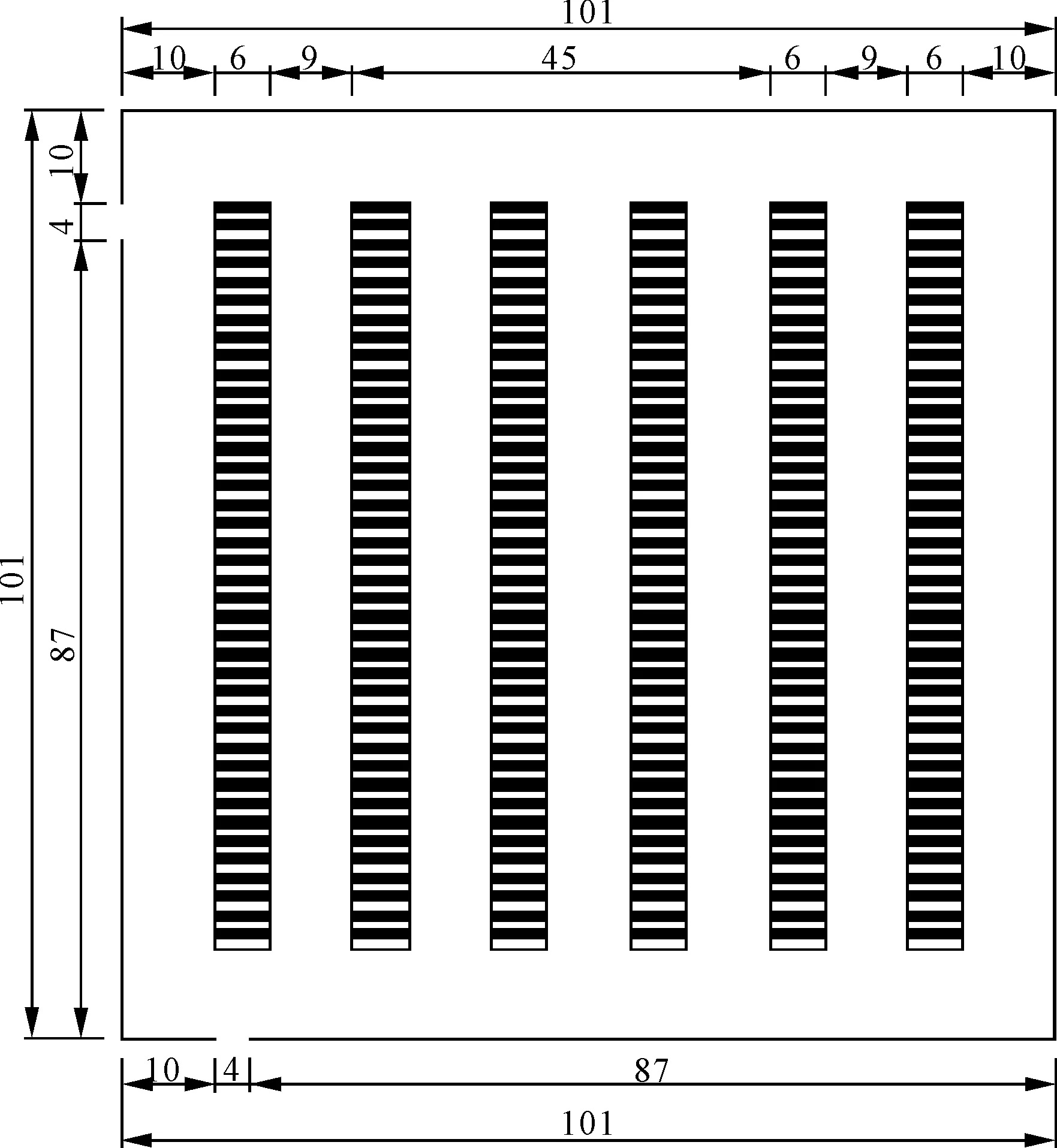
图3 双出口大型会议室布局图
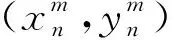
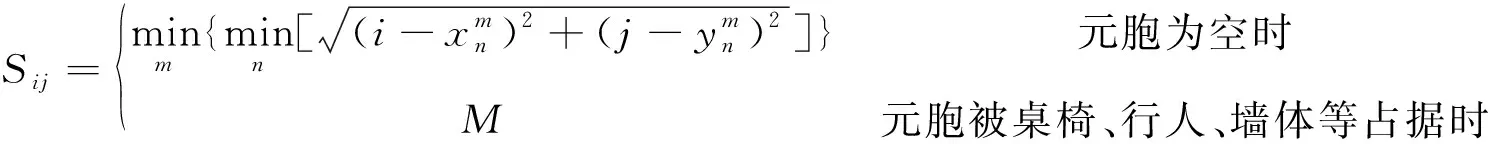
(1)
式中:(x,y)为行人在疏散区域的坐标;(xm,yn)为第m个门,第n个元胞在疏散中的坐标;M为常数。受座位区域影响,行人运动速度将减小。该区域的行人会选择离自身较近的过道作为运动方向。引入距离参量Lij=|i-xi|,xi为距离(i,j)最近的过道的元胞横坐标。
确定每一个元胞的位置危险度PD(i,j),比较行人领域内8个方向的元胞位置危险度,位置危险度最小的元胞为行人下一时刻的运动目标元胞;若运动目标元胞的位置危险度小于该行人所在元胞的位置危险度,则行人将运动到该元胞;若等于行人所在元胞的位置危险度,则行人以0.5的概率运动到目标元胞,以0.5的概率静止不动;若大于该行人所在元胞的位置危险度,则行人以0.2的概率运动到目标元胞,以0.8的概率静止不动;若运动邻域内存在多个位置危险度最小的元胞时,行人将以相同的概率随机选择一个元胞作为下一步的运动目标元胞[16]。元胞位置危险度PD(i,j)的计算如式(2)所示。
PD(i,j)=
(2)
模型采用并行更新,当行人之间存在冲突时,元胞自动机系统以相同概率随机选择一个行人占据元胞,被选中的行人移动到目标元胞,没被选中的行人保持原来位置不变。当行人移动到出口内时,表示该人已经离开疏散空间,将被移除疏散系统。为减小初始分布和行人的随机性对数据结果的影响,将所有仿真实验均重复运行20次取平均值,以保证实验数据的有效性。
2 疏散仿真与结果分析
2.1 安全出口对疏散时间的影响
(1)双出口间距不变时人员疏散分析
座椅布局与出口位置如图3所示。待疏散总人数设定为960人,安全出口宽度D分别取4、6、8个元胞宽度,出口位置由10到80变化。分别模拟各工况下人员疏散过程,统计疏散时间与出口位置关系。当出口宽度=4,出口位置=50,疏散时间步T=17 s时,疏散空间内人员疏散快照如图4所示。

图4 疏散空间人员疏散仿真快照
设定出口宽度分别为4、6、8,模拟出口位置变化下的疏散时间如图5所示。当出口宽度为4、6、8时,其疏散时间与出口位置的关系曲线均呈现“V”形态;出口位置设置为50,即出口位于墙体中间位置时,人员疏散时间最短。出口位置一定时,疏散时间随出口宽度增大而逐渐减小。

图5 不同出口宽度下疏散时间与出口位置关系
(2)双出口间距变化时人员疏散分析
为了方便分析,构建双出口均位于同侧墙上的疏散空间情景,其平面图如图6所示。
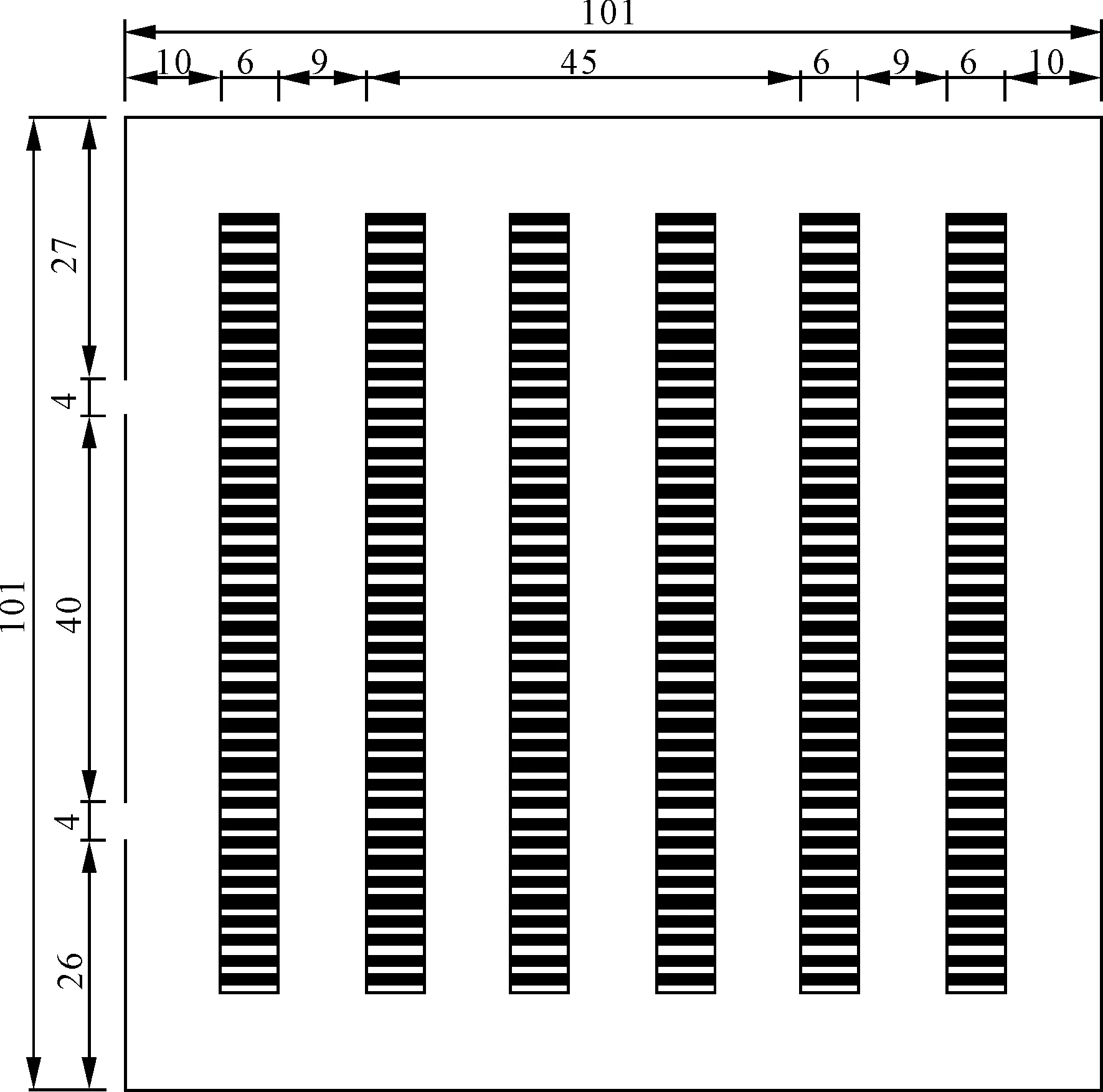
图6 同侧墙双出口疏散平面图
两个出口的宽度相同,分别取4、6、8、10,出口间距分别取10、20、30、40、50、60、70、80、90,其余参数与上述相同,疏散时间与出口位置、宽度的仿真结果如图7所示。
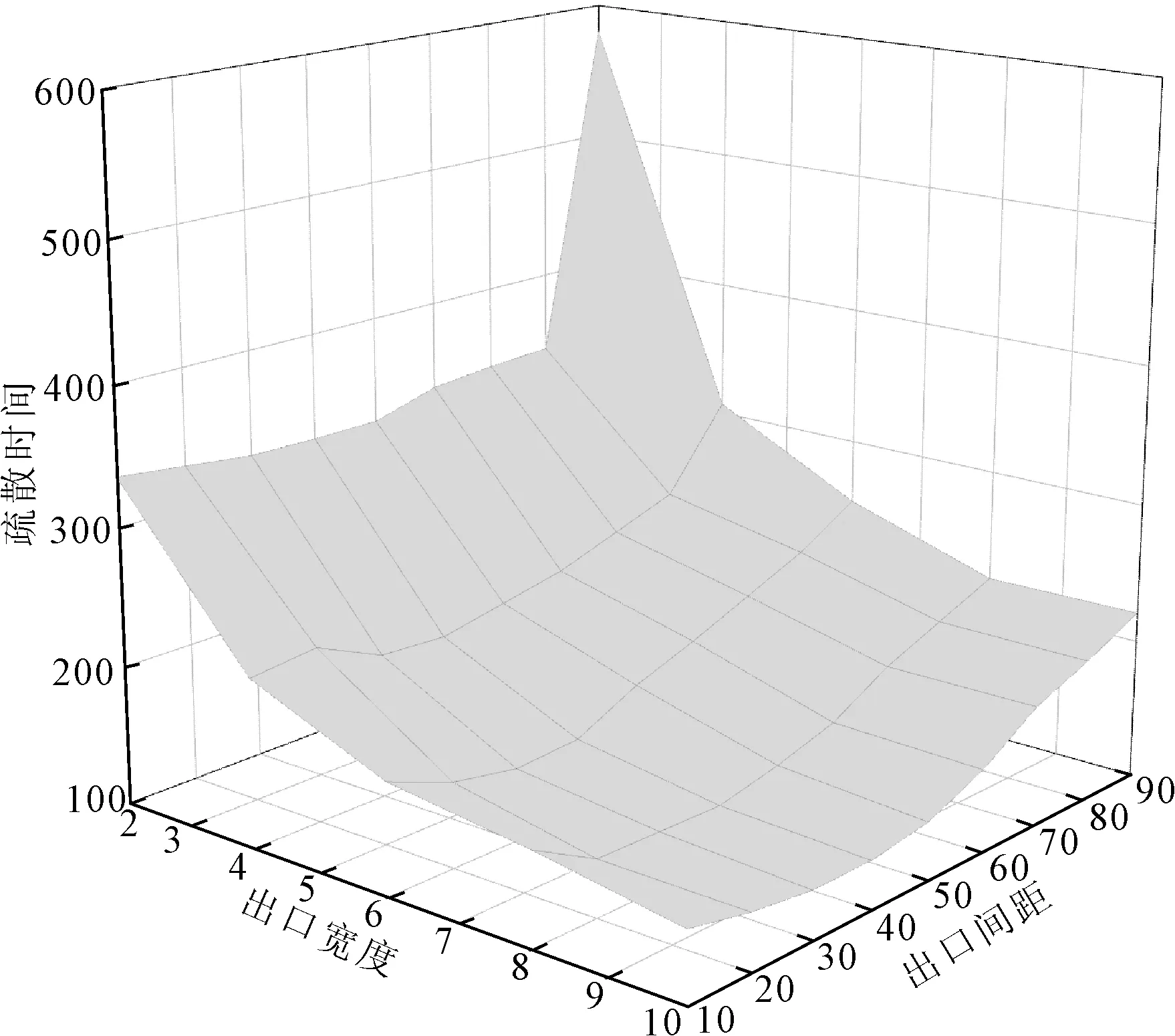
图7 出口间距、出口宽度与疏散时间关系
疏散时间与出口间距、出口宽度的关系呈现“沟谷”形态。出口宽度一定时,疏散时间随着出口间距的逐渐增大而呈现先减小后增大的趋势,即呈现“V”字型变化规律;出口间距一定时,疏散时间与出口宽度都呈幂函数衰减趋势,在出口宽度较小时衰减程度较大,当出口宽度达到某一特定值后,其衰减趋于平稳,几乎无显著变化。但在出口间距取30~40个元胞时,疏散时间均是最短的,考虑建筑结构实际情况与建筑防火规范要求,出口宽度取6个元胞时更加科学合理。
(3)双出口布局对人员疏散的影响分析
设置4种双出口布局形式:布局1(左侧+下面)、布局2(均在左侧))、布局3(左右侧居中)、布局4(上下底面居中)。设定模拟参数与上述相同,以出口宽度=4为例,分别模拟双出口不同布局形式下特定时间步的人员疏散过程,如图8所示。

图8 不同出口布局形式下疏散仿真情况
①布局1:T=90 s,人员集聚到出口附近;T=262 s,人员疏散完毕(见图8(a))。②布局2:T=75 s,人员集聚到出口附近;T=242 s,人员疏散完毕(见图8(b))。③布局3:T=40 s,人员集聚到出口附近;T=203 s,人员疏散完毕(见图8(c))。④布局4:T=37 s,人员集聚到出口附近;T=200 s,人员疏散完毕(见图8(d))。根据四种布局情景的疏散模拟分析,疏散时间由大到小依次为:布局1>布局2>布局3>布局4,但布局3和布局4的疏散时间基本相同。究其原因主要为:布局1情境下,疏散人员分别向两个出口运动,多数表现为斜向移动,需要穿越或绕过座椅向出口移动,空间距离较大;布局2相对布局1来说,空间运动距离相对小,疏散时间会减少;布局3和布局4情景下,疏散过程基本上呈现对称现象,疏散距离最短,但在实际工程中一般不会采用布局4这种形式。为进一步分析4种布局下出口宽度对疏散时间的影响,模拟4种布局下疏散时间与出口宽度的变化关系,如图9所示。当布局形式一定时,疏散时间随出口宽度的增加而减少,其中布局4的疏散时间随出口宽度的增加而下降得最快。
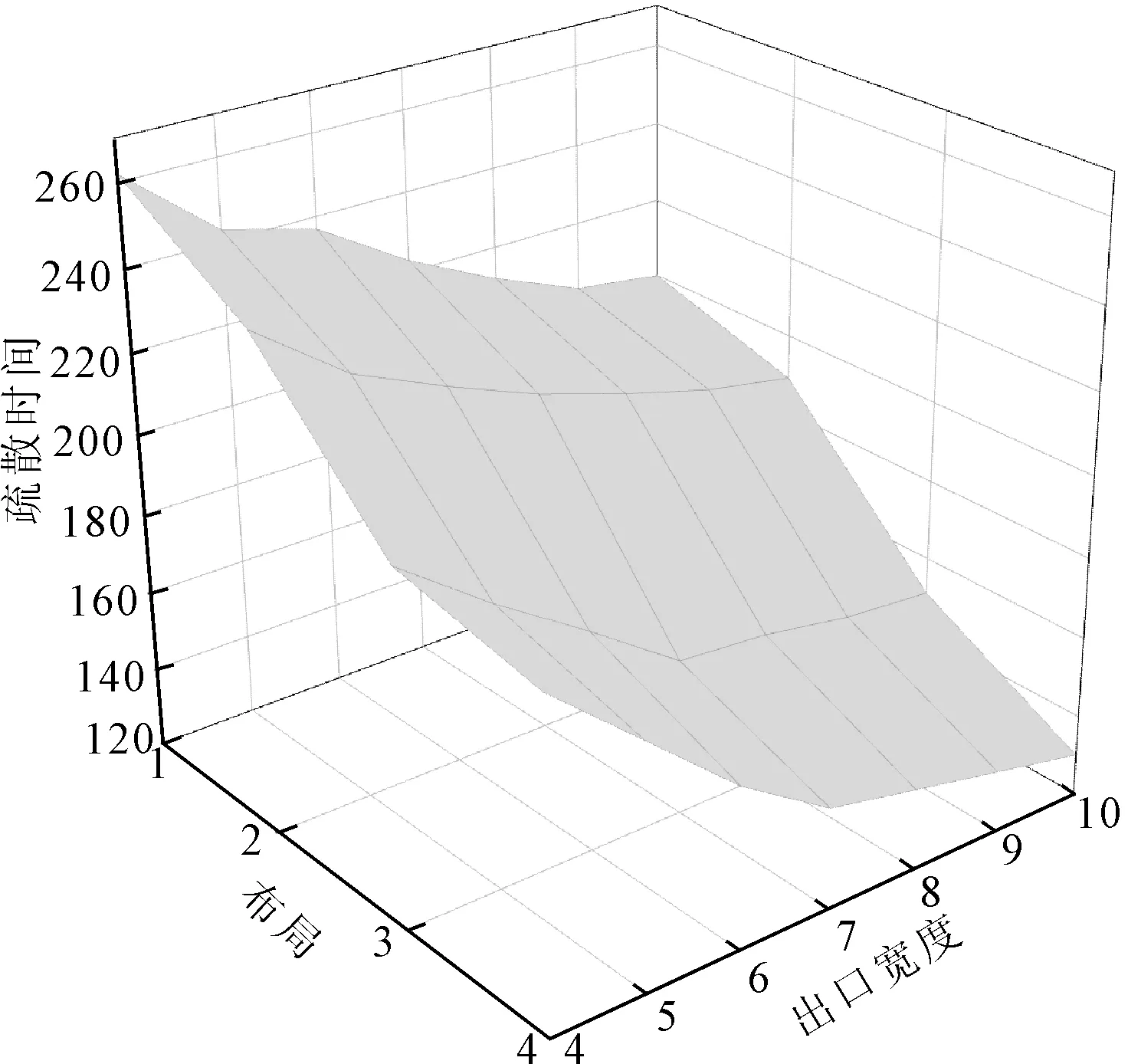
图9 四种布局形式下疏散时间与出口宽度的关系
(4)出口数量对人员疏散的影响分析
根据上述分析设置单出口、双出口、三出口、四出口4种情景,如图10所示。
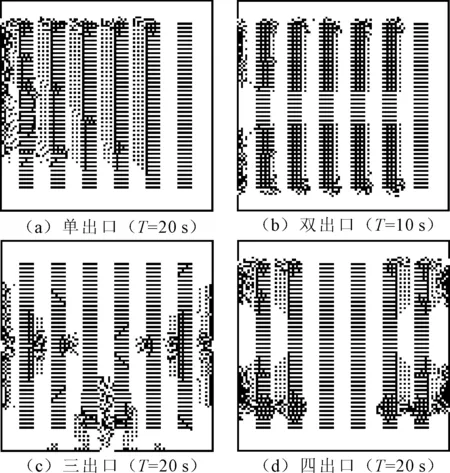
图10 不同情景下特定时间步的疏散仿真快照
分别模拟不同出口情景下疏散时间与出口宽度的变化关系,如图11所示。相同出口宽度下,单出口情景的疏散时间远大于其它3种布局情景,双出口、三出口和四出口情景下的疏散时间差别不是很大。单出口与双出口情景下的疏散时间步差值约在200~600 s之间,双出口与三出口情景下的疏散时间步差值约在50~100 s之间,三出口与四出口情景下的疏散时间步差值约在10~120 s之间。这表明单出口疏散时间最长,主要是人员在门口处排队等待时间较长,而增加安全出口数量后,人员能够快速疏散,排队等待时间较短,此时不断增加出口宽度对疏散时间的影响已不显著。
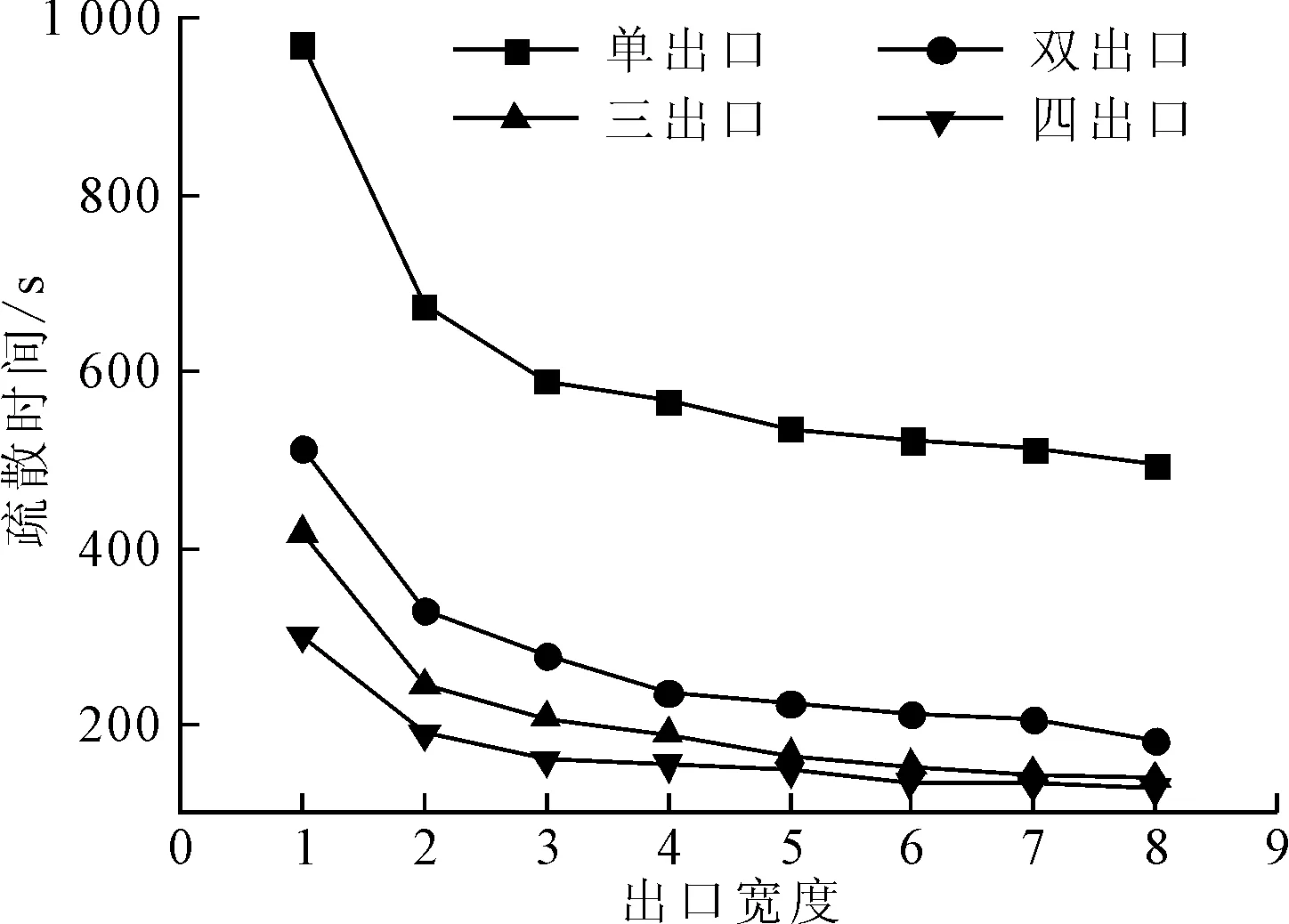
图11 疏散时间与出口宽度关系
2.2 桌椅布局对疏散时间的影响
根据图3设置参数如下:最左侧过道宽度不变(保持9个元胞),桌椅排数为40,桌椅列数分别取5、6、7、8、9、10,人员初始密度=0.5,其他参数同上。模拟分析疏散时间与桌椅列数的关系,并与单出口情景下的模拟结果对比,结果如图12所示。

图12 疏散时间与桌椅列数关系曲线
由于人员密度不变,随着桌椅列数的增加,疏散人数随之增加,疏散总时间也会增加。单出口、双出口情境下,疏散时间与桌椅列数曲线均呈上升趋势,但前者的斜率较大,表明双出口情景的人员疏散效率明显高于单出口情景;课桌列数越多,两者的疏散时间差越大,但随着课桌列数越多,会逐渐牺牲疏散通道的有效利用面积,不利于紧急情况时大型会议室内人员的疏散。因此,双出口布局情景下,考虑会议室内疏散通道要求,建议桌椅最佳列数为6列。
2.3 人员密度对疏散时间的影响
设定人员密度由0到1变化,其余参数不变,模拟分析大型会议室座位区域上人员的分布密度对疏散行为的影响,并与单出口情景下进行对比分析,结果如图13所示。由图可知,单出口、双出口情景下,疏散时间与人员密度关系曲线均呈上升曲线,前者所有时间大于后者;对比疏散时间,单出口情景比双出口情景要多20~40 s,表明人口密度越大,两者疏散时间差距越大。
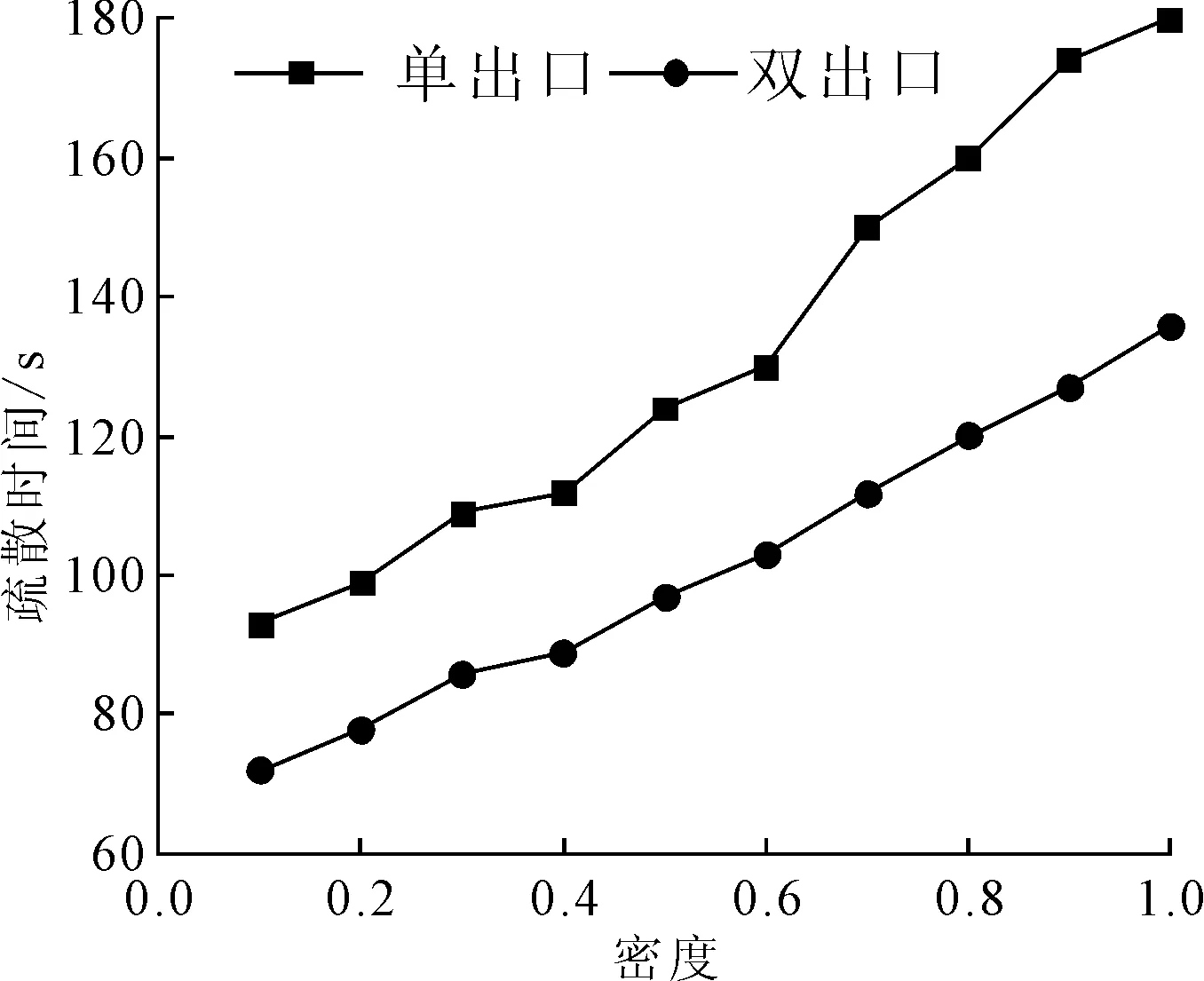
图13 疏散时间与人员初始密度之间关系
3 结论
针对大型会议室疏散空间优化的问题,采用Moore型邻域的元胞自动机方法建立了考虑障碍的大型会议室人员疏散元胞自动机模型,模拟大型会议室紧急事件下人员疏散行为及疏散空间特性,结合建筑实际与规范要求提出大型会议室疏散空间的优化建议,得出以下结论:
(1)疏散时间与出口间距、出口宽度的关系呈现“沟谷”形态;疏散时间与出口位置的关系曲线均呈现“V”形态,疏散时间与出口宽度关系曲线呈幂函数衰减趋势。单侧单出口位于墙体中间时,人员疏散效率最高;单侧双出口间距设置在12~16 m之间、出口宽度取6 m较为合理且符合实际。
(2)在双出口不同布局形式中,两侧中间位置对称设置安全出口对室内人员疏散最为有利,单侧双出口(间距位于12~16 m之间)的疏散效率次之。出口数量对室内人员疏散效率产生一定的影响,但随着安全出口数量的增加,室内人员疏散效率不会显著提升。
(3)疏散时间与桌椅列数、人员密度的关系曲线均呈上升趋势;随着课桌列数增加,将会逐渐牺牲疏散通道的有效利用面积,不利于紧急情况时大型会议室内人员的疏散。考虑会议室内疏散通道要求,建议桌椅最佳列数取6列。

