隧道管棚支护对上部铁路路基列车振动传播规律影响研究

董 捷,杨 博,王小敬,刘建友

(1.河北建筑工程学院土木工程学院,河北张家口 075000； 2.河北省寒冷地区交通基础设施工程技术创新中心,河北张家口 075000； 3.北旺集团有限公司,河北承德 067000； 4.中铁工程设计咨询集团有限公司,北京 100055)

引言

近年来，我国对地下空间的开发规模日益扩大。随着大规模地下工程的开工建设，由于受到既有路基限制，出现了大量新建隧道下穿既有铁路的复杂工程。当列车运行通过隧道正上方时，隧道结构和地层在上部列车振动荷载作用下可能会产生振动变形等危险，继而影响列车运行安全。为减少此类危险，保证隧道施工与运营期间安全，工程中常采用管棚支护措施对隧道进行支护，而超前支护的存在，可有效减小上部振动荷载产生的围岩变形。但通常由于此类工程较为复杂，工程中常会遇到各种难题，因此，研究管棚支护上部地层振动传播规律具有重要的现实意义。

目前，国内外诸多学者对类似工程进行了大量分析研究[1-5]。一部分学者对地下穿越结构受列车振动荷载影响下结构与围岩变形进行了研究[6-10]，认为上部既有路基的振动荷载会对下部穿越隧道的安全性产生影响[11-12]。此外，还有部分学者对采用管棚支护的类似穿越工程进行了分析[13-15]，但此类研究多为静载作用下开挖施工引起的一系列问题[16-18]，而特别针对列车振动荷载对类似工程影响的研究很少。由于此类工程施工安全要求高，进行现场实测难度较大，且构建力学解析模型也相对复杂。鉴于此，针对列车运行通过上部路基交叉点这一特殊情况，采用室内模型试验与数值模拟相结合的方法，对不同管棚间距下列车振动传播规律进行研究，分析管棚间距对地层振动加速度与动位移的影响，得到合理管棚间距，以期为类似工程提供借鉴。

1 列车振动荷载模拟

列车荷载的确定是一个非常复杂的问题，常用的列车荷载确定方法有实测加速度法和经验公式法，由于荷载现场实测难度较大，受限于试验条件，本次采用经验公式法对其进行确定[19]。采用激振力函数模拟高速列车荷载，包括静荷载和一系列随机荷载[20-21]。其具体表达式为

P(t)=P0+P1sinω1t+P2sinω2t+P3sinω3t

(1)

式中，P0为车轮静载；P1、P2、P3为振动荷载，分别对应按行车平稳性、按作用到线路上的动力附加荷载以及波形磨耗3种情况。

列车簧下质量为m0，则相应的振动荷载幅值为

(2)

式中，ai为3种情况下的典型矢高；ωi为对应车速下，相应3种情况不平顺振动波长下的圆频率。

圆频率计算公式为

(3)

式中，v为列车运行速度；Li为3种情况下的典型波长。

计算时取单边静轮重P0=80 kN，簧下质量m0=750 kg，车速为324 km/h。波长和矢高具体为：L1=10 m，a1=3.5 mm；L2=2 m，a2=0.4 mm；L3=0.5 mm,a3=0.08 mm,其是根据我国铁路运行标准选取的。激振力函数如图1所示。

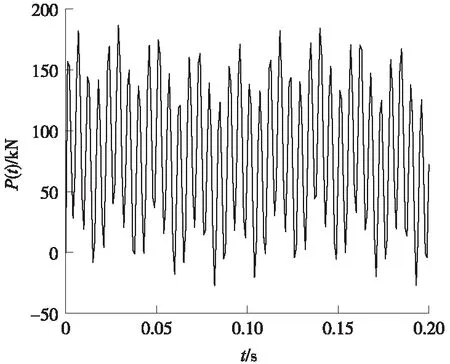
图1 激振力与时间的关系

2 室内模型试验

2.1 试验介绍

通过对模型箱内的路基模型相应位置施加列车荷载，以模拟隧道下穿路基段管棚支护的实际工作状态，进而得到一些规律性的认识。本试验针对列车运行通过隧道正上方，即通过交叉点时，不同管棚间距下的列车振动传播规律进行研究，分析不同管棚布置方案下列车振动荷载对管棚结构上部地层的影响。室内模型试验装置基本情况如图2所示。

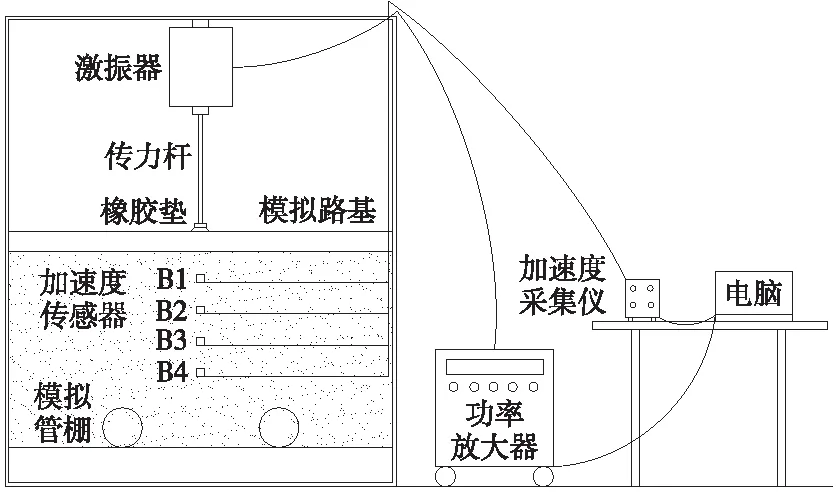
图2 室内模型试验平面示意

模型箱整体框架为角钢，正面为透明亚克力板，其余面安装钢板，长、宽、高分别为800，500，1 000 mm。模型箱底部留有空隙，用于模拟隧道，空隙上部可架设模拟管棚，如图3所示。在特定加载范围内，须确保选择的管棚模型处于线弹性工作状态，试验采用PVC管作为管棚模型，管壁厚3 mm。受限于试验条件，模型试验选取相邻2根管棚作为研究对象。

2.2 试验步骤

(1)在模型箱底部固定模拟管棚，管棚下方放入水袋并充满水，保证填料过程没有材料掉下。

(2)模型箱四周布置高密度泡沫板，减小试验中振动波的反射，保证试验的正确性。

(3)分层填筑，每5 cm填筑一次，试验中采用的填料为含水量10%的粉细砂，填筑过程中在设计位置布设加速度传感器，布置位置见图2。

(4)在相应位置布置铁轨模型，保证车道模型与激振器上的传力杆紧密接触，传力杆采用φ18 mm光圆钢筋，与铁轨接触的一段焊接一块φ3 cm圆形铁片，底部固定等大小的橡胶垫，防止传力杆与车道直接接触。

(5)填筑完成之后，打开下方水袋，将水放出，此步骤模拟开挖卸荷过程。

(6)加载，并采集数据，加载时间保持1 min的稳定时间，停止加载，停止采集。

(7)重复上述步骤，进行多工况试验，共设置6种工况，管棚间距分别为6，9，12，15，18，21 cm。实验过程如图4所示。

图4 试验过程

2.3 试验结果分析

列车荷载作用下管棚上部地层加速度时程如图5所示，各个管棚间距下加速度时程曲线差异不大，本次仅列出间距为12 cm的工况。

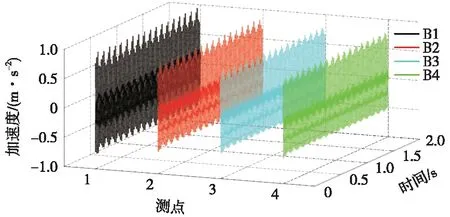
图5 测点加速度时程曲线

列车荷载作用时，各间距下测点B1、B2、B3、B4加速度峰值衰减曲线如图6所示。

图6 加速度峰值衰减曲线

分析图5、图6可以得到以下结论。

(1)加速度监测点B1、B2、B3、B4的加速度时程曲线相似，波形具有较好的规律性，改变管棚间距不会改变监测点的加速度时程曲线形态，加速度时程曲线具有明显的振动峰值，并呈现明显的周期性变化。

(2)列车荷载作用下地层的加速度随距离路基增加而减小，以管棚间距为21 cm为例，相对距离路基最近的B1测点，B2、B3、B4监测点的加速度峰值分别减小了0.082，0.124，0.138 m·s-2。

(3)随着距上部路基距离增加，加速度峰值衰减逐渐变慢。以管间距为18 cm时为例，监测点B1、B2、B3、B4的加速度峰值分别为1.030，0.959，0.906，0.891 m·s-2，可以看出，监测点B2相对B1，加速度峰值衰减了6.7%；监测点B3相对B2，加速度峰值衰减了5.5%；监测点B4相对B3，加速度峰值衰减了1.7%。

图7为列车荷载作用时各个测点在不同管棚间距下的加速度峰值变化曲线。

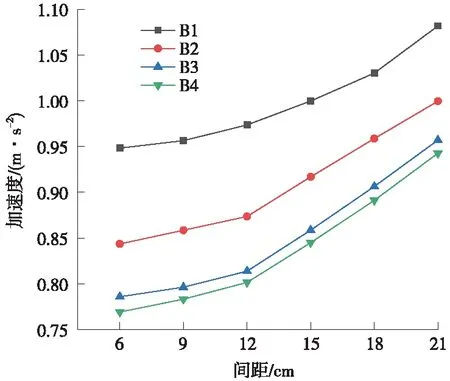
图7 加速度峰值随管棚间距变化曲线

分析图7可以得到以下结论。

(1)随着管棚间距变小，监测点加速度峰值逐渐变小。以监测点B1为例，管间距分别为21，18，15，12，9，6 cm时，加速度峰值分别为1.082，1.030，0.999，0.973，0.956，0.948 m·s-2。

(2)当管棚间距减小到一定范围时，测点加速度峰值减小的程度变小，当管棚间距从21 cm减小到12 cm过程中，加速度峰值减小程度较大，当管棚间距减小到12 cm时，再次减小管棚间距对加速度峰值的影响不大。以监测点B1为例，从间距21 cm减小到12 cm过程，加速度峰值分别减小了0.052，0.031，0.026 m·s-2；从间距12 cm缩小到6 cm的过程，加速度峰值分别减小了0.017，0.008 m·s-2。

3 数值模拟

受限于试验条件，模型试验部分选取了相邻两根管棚为研究对象。鉴于此，为更好地模拟实际情况，本节采用数值仿真手段对完整的隧道下穿路基段管棚支护进行模拟，以研究管棚间距对地层振动传播规律的影响。

3.1 模型建立

采用三维有限差分软件建立动力分析模型，模拟隧道下穿路基段管棚支护的动态承载特性。指定上部铁路路基方向为X轴正向，下部隧道方向为Y轴正向，竖直向上为Z轴正向。结合某实际工程，下部隧道设计洞跨为13 m，高9 m(高度为仰拱底至拱顶的高差)，隧道与上部高速铁路路基交叉角度为90°，隧道顶板至路基底部距离8 m。为减小边界效应的影响，经过大量计算，确定了模型尺寸为65 m(长)×30 m(宽)×44 m(高)。在数值模拟研究中，可将管棚支护的加固效果视为在隧道开挖轮廓线以外形成了环形加固圈，采用改善围岩参数的方法进行模拟[22]。计算模型如图8所示。结构参数见表1。

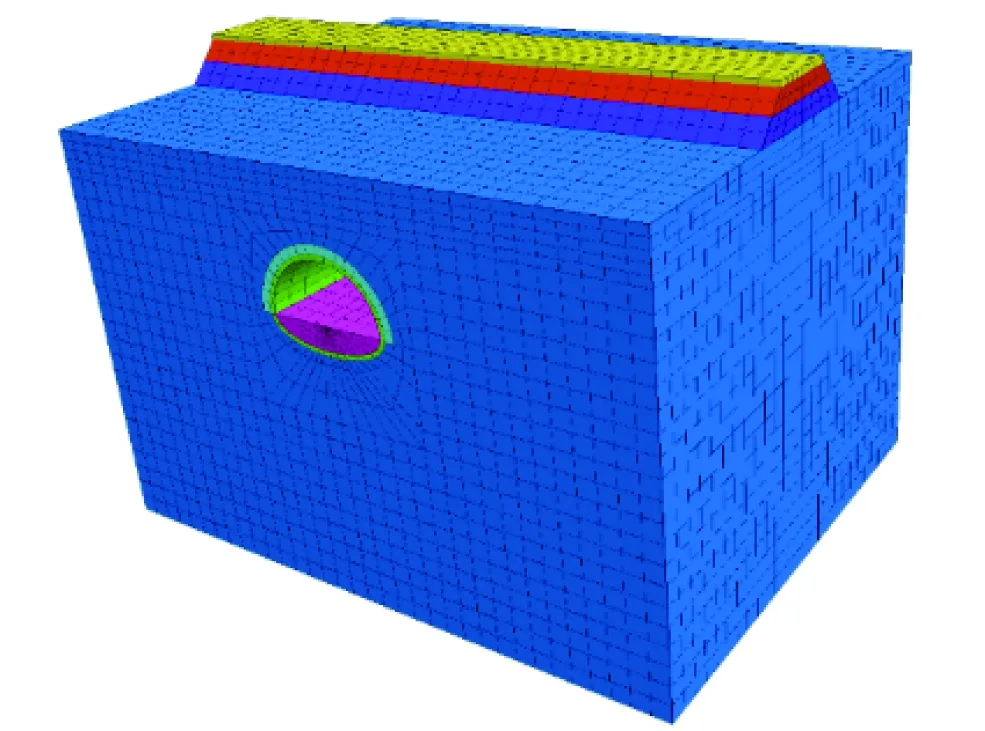
图8 计算模型

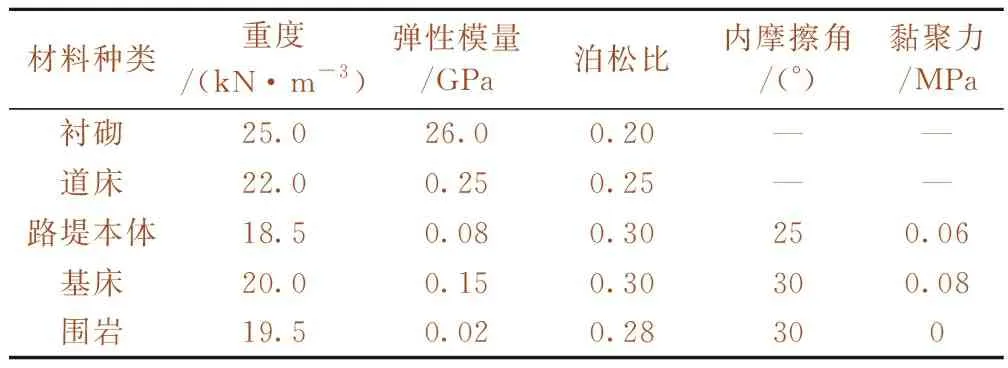
表1 结构参数

3.2 计算工况

目前，工程中常用的管棚为φ108 mm，而工程中管棚环向间距的布置通常为30～60 cm，鉴于此，选取管棚间距30，35，40，45，50，55，60 cm作为计算工况。对各工况加固区等效弹性模量进行计算[23]，如表2所示。

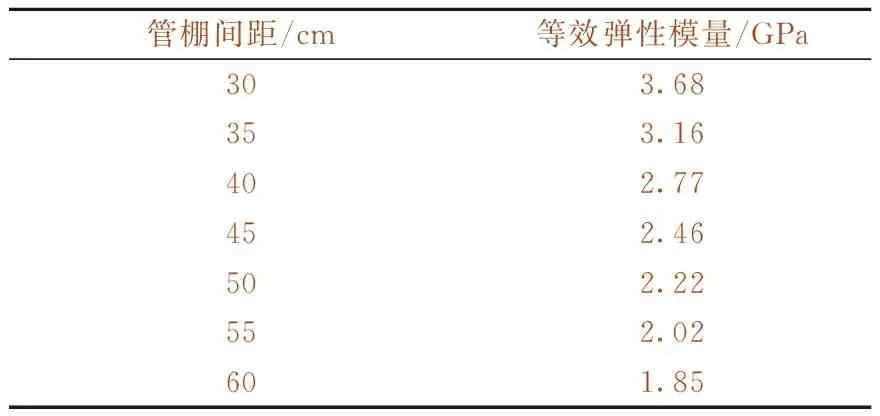
表2 各工况等效弹性模量

3.3 监测点布置

为研究管棚间距对地层振动传播规律的影响，数值模拟中在交叉段地层自路基底部至加固区由上而下布置了8个监测点。由于试验中监测位移较为困难，模拟中对各监测点的加速度与动位移进行了监测。监测点布置如图9所示。

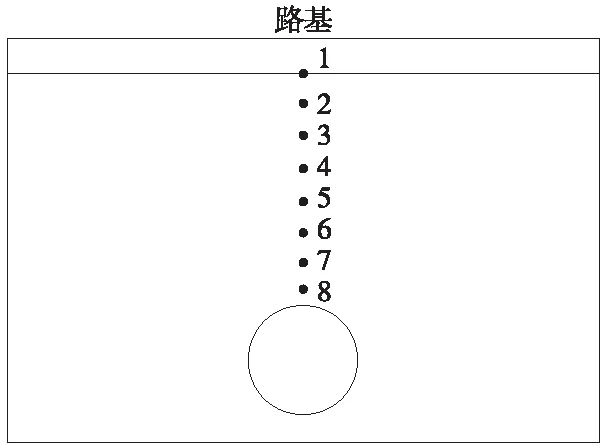
图9 地层监测点竖直向布置示意

3.4 加速度分析

图10为各管棚间距下地层自上而下加速度峰值衰减曲线。

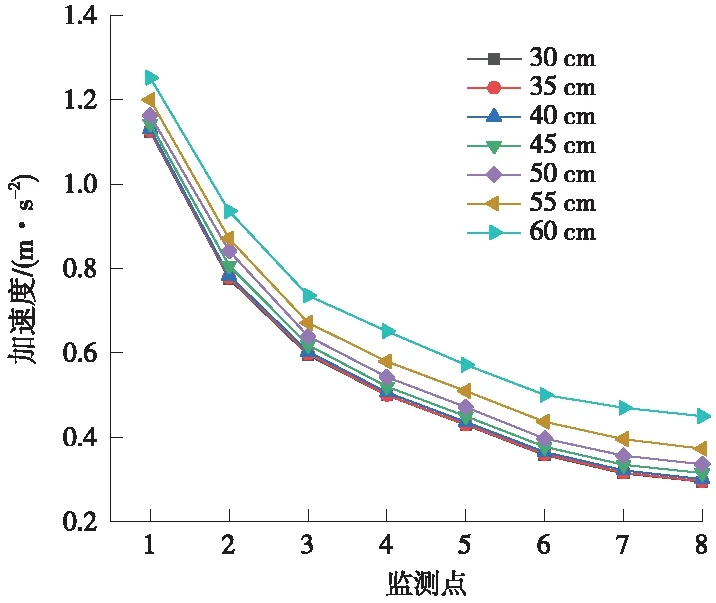
图10 地层加速度峰值衰减曲线

由图10可以得到以下结论。

(1)列车振动荷载作用下地层的加速度峰值随距离路基距离的增加而逐渐减小。以间距40 cm为例，监测点1～8的加速度峰值分别为1.131,0.783,0.603,0.506,0.436,0.365,0.322 m·s-2和0.301 m·s-2。

(2)分析曲线可以看出，曲线趋于平缓，即距离上部路基越远，加速度峰值衰减速度越慢。继续以管棚间距40 cm为例，相对测点1，测点2的加速度峰值衰减了30.8%；测点3相对测点2衰减了23.0%；测点4相对测点3衰减了16.1%；测点5相对测点4衰减了13.8%；测点6相对测点5衰减了16.3%；测点7相对测点6衰减了11.8%；测点8相对测点7衰减了6.5%。

(3)改变管棚间距，只会改变各测点的加速度峰值，不会改变地层的加速度衰减规律，各管棚间距下地层的加速度衰减规律相同。

图11为各监测点在不同管棚间距下的加速度峰值变化曲线。

图11 地层加速度峰值随管棚间距变化曲线

由图11可以得到以下结论。

(1)随着管棚间距变小，各监测点加速度峰值逐渐变小。以测点1为例，当管棚间距分别为60，55，50，45，40，35，30 cm时，其加速度峰值分别为1.251，1.199，1.162，1.143，1.131，1.126，1.124 m·s-2。

(2)当管棚间距缩小到一定范围时，各测点的加速度峰值不再明显减小。当管棚间距从60 cm缩小到40 cm过程中，加速度峰值减小明显；当管棚间距缩小到40 cm之后，继续缩小间距对各测点的加速度峰值影响不大。以测点1为例，在管棚间距从60 cm缩小到40 cm时，加速度峰值分别减小了0.052，0.037，0.019，0.012 m·s-2；而从40 cm缩小到30 cm过程中，加速度峰值分别减小了0.005，0.002 m·s-2。

可以看出，数值模拟部分与模型试验部分得出的结论较为一致。管棚间距会对地层加速度响应产生影响，减小管棚间距会使各个测点的加速度峰值变小。

3.5 动位移分析

图12为管棚间距为40 cm时各个测点的动位移时程曲线(限于篇幅，其余工况曲线相同)。

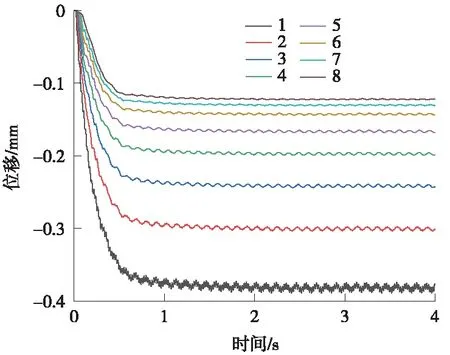
图12 各测点位移时程曲线(间距40 cm)

由图12可以看出，各测点位移时程曲线呈现相同的波形，且其形态与输入的激振力形态相似。距路基距离的改变不会改变各测点的位移时程形态，但距离路基越近，位移时程曲线的振动幅值越大，且其位移峰值越大。以管棚间距40 cm为例，测点1～8的位移峰值分别为0.389，0.304，0.244，0.199，0.168，0.144，0.131，0.123 mm，说明距离路基越近，列车振动荷载对地层影响越大。

图13为各管棚间距下地层自上而下的位移峰值变化曲线。

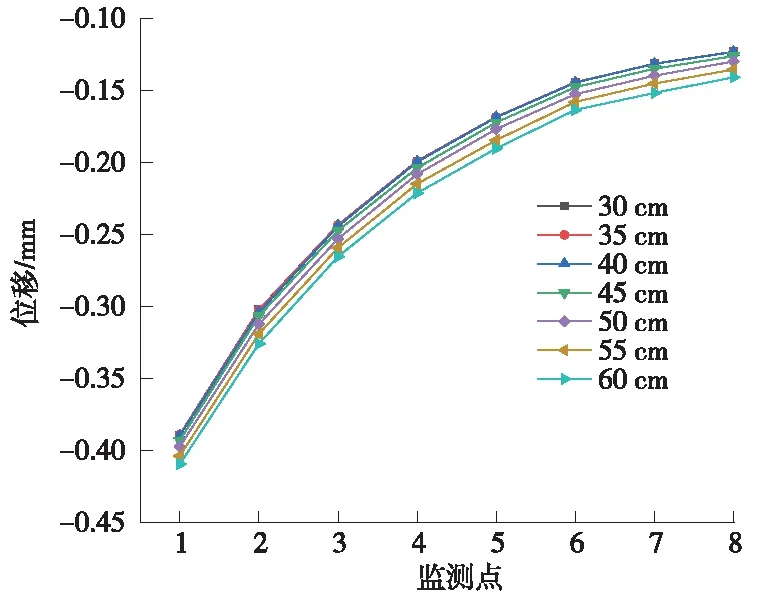
图13 地层位移峰值衰减曲线

由图13可以得出以下结论。

(1)列车振动荷载作用下，各测点的位移峰值随距上部路基距离增加而减小。测点1位移最大，测点8最小。这说明由于地层阻尼等因素影响，振动荷载在地层中传播时，振动波的能量逐渐减小。

(2)随着距路基距离的增加，位移峰值衰减逐渐变慢，距离路基越远，振动影响越小，衰减越慢。以管棚间距为40 cm为例，相对测点1，测点2的位移峰值衰减了21.9%；测点3相对测点2衰减了19.7%；测点4相对测点3衰减了18.4%；测点5相对测点4衰减了15.6%；测点6相对测点5衰减了14.3%；测点7相对测点6衰减了9.0%；测点8相对测点7衰减了6.1%。

(3)改变管棚间距，只会改变各个测点的位移峰值，不会改变其衰减规律，各管棚间距下地层的位移衰减规律相同。

图14为各监测点位移峰值随管棚间距变化曲线，图15为监测点1在不同管棚间距下的位移峰值变化曲线。

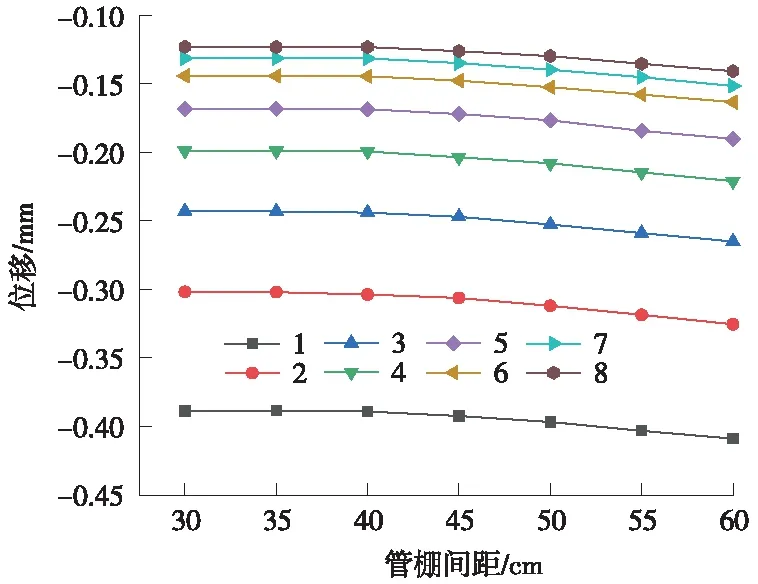
图14 地层位移峰值随管棚间距变化曲线

图15 测点1位移峰值随管棚间距变化曲线

由图14、图15可以得出以下结论。

(1)由图14可知，随着管棚间距减小，各测点位移峰值逐渐变小。以测点1为例，当管棚间距分别为60，55，50，45，40，35，30 cm时，其位移峰值分别为0.409，0.404，0.397，0.393，0.389，0.388，0.388 mm。

(2)随着管棚间距变小，各测点的位移峰值减小程度变小，当管棚间距缩小到40 cm之后，继续缩小管棚间距对测点位移峰值影响很小。图14中变化趋势不太明显，由图15可以看出，在管棚间距由60 cm减小到40 cm过程中，测点1的位移峰值分别减小了0.005，0.007，0.004，0.004 mm；而在管棚间距由40 cm减小到30 cm时，测点1的位移峰值变化很小。

4 结论

通过分析隧道管棚支护对上部铁路路基列车振动传播规律的影响，针对列车运行通过交叉点时进行了模型试验与数值模拟研究，分析管棚间距对地层振动传播规律的影响。对地层的加速度响应进行了监测，模型试验与数值模拟部分振动加速度规律一致，此外还在数值模拟中对地层的动位移进行了监测，并根据模型试验与数值模拟结果得到了合理管棚间距。主要研究结论如下。

(1)列车振动荷载作用下，地层加速度峰值随距路基距离的增加而逐渐减小。即距离上部路基越远，加速度峰值衰减速度越慢。改变管棚间距，只会改变各测点的加速度峰值，不会改变地层的加速度衰减规律，各管棚间距下地层的加速度衰减规律相同。

(2)数值模拟部分与模型试验部分得到了相同的结论。管棚间距会对地层加速度响应产生影响，管棚间距越小，各测点的加速度峰值越小，当管棚间距缩小到一定范围时，各测点的加速度峰值不再明显减小。

(3)管棚间距改变会影响地层的动位移，随着管棚间距减小，各测点的动位移随之减小，但当管棚间距缩小到40 cm之后，继续缩小管棚间距对测点位移峰值影响很小。

(4)数值模拟中振动加速度与动位移在管棚间距由60 cm减小到40 cm的过程中变化较大，而在由40 cm减小到30 cm的过程中变化很小。因此认为本文条件下管棚间距为40 cm较为合理。