MTC装置布设方案对铁路连续梁桥减震影响研究

许鑫祥,陈士通,张茂江,李 然

(1.石家庄铁道大学河北省交通应急保障工程技术研究中心,石家庄 050043； 2.石家庄铁道大学国防交通研究所,石家庄 050043； 3.石家庄铁道大学土木工程学院,石家庄 050043)

连续梁桥结构简单，行车舒适，养护费用较低，在我国铁路运输中得到了广泛应用。然而，中小跨度铁路连续梁桥的一联只设置一个固定墩来满足温度荷载引起的梁体变形需求，地震作用下上部结构产生的纵向地震荷载全部由固定墩承担[1-2]，这不仅导致了固定墩弯剪破坏，而且增加了梁体纵向位移，易造成伸缩缝和支座破坏，甚至引发落梁等严重震害[3-4]。对于道岔区中小跨度铁路连续梁桥而言，地震作用还易导致轨道结构发生屈曲、失稳等现象[5]，对桥梁正常运营造成严重影响。

为减小桥梁地震损伤，国内外学者通过研发各种减震装置来提高连续梁桥抗震性能。刘正楠等[6]探究了在铁路连续梁桥上应用摩擦摆支座后减震体系的受力状态；张常勇等[7]进一步分析了应用摩擦摆支座时连续梁桥地震能量反应；董俊等[8]提出一种大跨铁路桥梁金属限位减震装置，并对其力学性能进行探究；白全安[9]提出一种新型减隔震限位装置，并对其在铁路桥梁上的适用性做了深入探究；Lock-up装置也称为速度锁定器，其激活状态与体系速度有关[10-11]，全伟等[12]以一座长联公铁两用钢桁梁桥为例，分析了Lock-up装置的减震性能；李锋等[13-14]提出了加速度激活的IFA装置，深入探究了装置工作原理及对连续梁桥工作性能的影响，并对比分析Lock-up装置和IFA装置的减震效果，发现IFA装置的工程环境适用性更强；陈士通等[15]提出了一种加速度激活的锁死销减震装置，探究了装置减震机理；张文学等[16]进一步分析了锁死销装置在非规则连续梁桥上应用时的减震效果；FANG等[17-18]进一步通过振动台模型试验对锁死销主要参数进行了优化，还提出了一种桥梁安全带装置，采用数值模拟和振动台试验相结合的方式对其减震机理进行了探究；许鑫祥等[19]提出一种位移激活的分阶段适时连接控制装置(Multi-stage Timely Connection Control，简称MTC)，其结构简单，可靠性较高。

已有研究已表明，在活动墩上安装MTC装置可提高连续梁桥抗震性能[19]，但已有研究多以大跨度连续梁桥为分析对象，针对中小跨度铁路连续梁桥的减震研究尚未有涉及。中小跨度铁路连续梁桥多出现于道岔区，地震发生时如其出现损伤现象，将影响整个铁路网络的正常运行。在前述研究基础上，进一步对MTC装置的合理布设方案进行深入探究：对连续梁桥MTC减震体系进行理论分析，并以某道岔区7跨连续梁桥为例，采用数值模拟分析了MTC装置在不同布设方案下的减震效果及桥梁地震响应情况，得到了布设位置和布设数量对其影响的一般规律。研究结果可为MTC装置在中小跨铁路连续梁桥上的应用提供技术支撑。

1 MTC装置

MTC装置安装在活动墩与梁体之间，是一种利用墩梁相对位移激活的减震装置，主要部件有水平连杆、锁紧螺母、限位装置(软钢挡板、金属橡胶及弹簧)和连接牛腿，如图1所示。限位装置分为Ⅰ区限位装置和Ⅱ区限位装置，均与活动墩相连。水平连杆穿过限位装置的空心区域，两端与固定在梁体上的牛腿铰接。锁紧螺母与Ⅰ、Ⅱ区限位装置之间分别预留间隙Δ1和Δ2，且Δ1<Δ2。

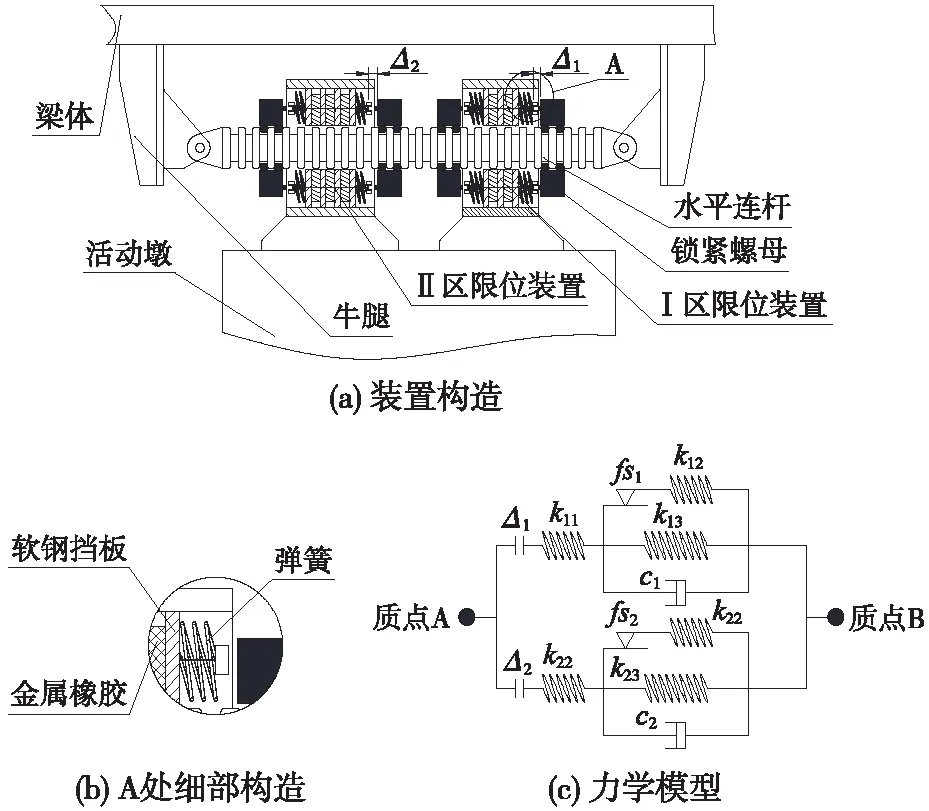
图1 MTC装置构造及力学模型

地震力作用下，装置激活时，限位装置与锁紧螺母接触，活动墩与梁体通过限位装置中的软钢挡板等实现弹性连接，二者相对运动受到限制，进而使活动墩参与抵抗水平地震力，同时，实现耗能减震(在弹簧压缩至一定程度后，软钢挡板和金属橡胶发生形变，三者共同消耗地震能量)。桥梁正常运营状态下，连续梁桥的最大墩梁相对位移小于Δ1，装置不激活；中小震作用下，墩梁相对位移大于Δ1，Ⅰ区限位装置激活；地震力进一步增大时，墩梁相对位移超过Δ2，Ⅱ区限位装置激活，此时Ⅰ、Ⅱ区限位装置同时发挥减震耗能作用。根据装置应用场地条件及墩高、跨度等桥梁结构参数，设置合理的MTC装置参数(激活间隙、限位刚度)，并选择合理布设方案，即可根据地震力大小实现分级减震，取得较好的减震效果。

图1(c)为装置力学模型，Δi、fsi、ci(i=1、2)分别为Ⅰ、Ⅱ区限位装置的激活间隙、屈服力、阻尼；kmn(m=1、2；n=1、2)代表限位刚度值，其中，m=1、2分别代表Ⅰ、Ⅱ区限位装置，km1、km2+km3、km3分别代表限位装置中的弹簧刚度、软钢挡板和金属橡胶组合的初始刚度、软钢和金属橡胶组合的屈服后刚度。

2 连续梁桥MTC减震体系理论分析

顺桥向地震荷载作用下，桥墩不考虑轴向变形时，地震荷载几乎全部来源于上部结构，因此，可将安装MTC装置的连续梁桥简化为上部梁体提供质量m，固定墩和安装MTC装置的活动墩提供抗侧移刚度的单自由度体系进行理论分析，简化体系如图2所示。c为体系阻尼；N为安装MTC装置的活动墩个数；MTC装置激活后，第i个活动墩与MTC装置串联后的刚度为kslide，i，固定墩所提供刚度为kfix。

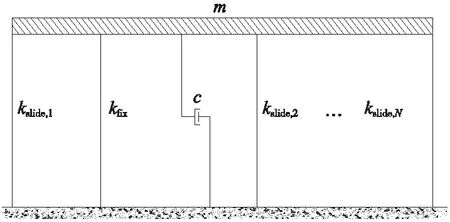
图2 简化单自由度体系

以基底剪力为例，对各活动墩与固定墩墩底响应极值进行分析，该体系运动方程为

(1)

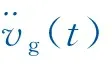
(2)

式中，ω为该体系自振圆频率；ξ为结构阻尼比。已知基底最大弹簧力为

fs，max=kv(t)max

(3)

将式(2)代入式(3)得

(4)

又知

(5)

将式(5)代入式(4)，则最大弹簧力可表示为

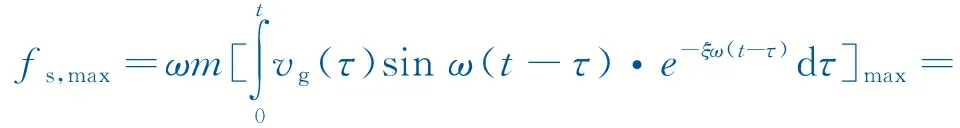
(6)

式中，Spa为谱绝对加速度，即结构自振周期对应的地震波加速度反应谱谱值[20]，表达式为

(7)

因此，连续梁桥整体剪力响应最大值为

Qmax=mSpa

(8)

地震力在各桥墩之间按抗侧移刚度分配，第i个活动墩剪力极值用Qslide，i表示，固定墩剪力极值用Qfix表示。则有

(9)

(10)

(11)

设kpier，i为第i个活动墩自身刚度，kMTC，i为安装在第i个活动墩上的MTC装置介入刚度，则活动墩与MTC装置串联后刚度为

(12)

联立式(8)～式(12)即可得连续梁桥在地震荷载下固定墩及安装MTC装置的活动墩墩底剪力极值表达式，如式(13)、式(14)所示。

(13)

(14)

由式(13)、式(14)可知，对任意连续梁桥MTC减震体系而言，活动墩地震响应大小由活动墩刚度、MTC装置刚度、MTC装置布设数目及地震波反应谱谱值确定；固定墩地震响应大小由固定墩自身刚度、活动墩刚度、MTC装置刚度、MTC装置布设数目及地震波反应谱谱值确定。对墩高相差不大的中小跨度铁路连续梁桥而言，各墩间刚度相差较小，各活动墩上的MTC装置刚度设置相同时，固定墩及活动墩地震响应主要由地震波反应谱及MTC装置布设数目确定。

3 工程概况及分析模型

为探究MTC装置在小跨铁路连续梁桥上应用时，减震效果受布设方案影响情况，选取图3所示7×32 m道岔区铁路连续梁桥为分析对象。该桥梁体采用单箱双室斜腹板等高度箱梁，梁高3.1 m，箱梁顶宽12.79 m，底宽6.85 m，梁体混凝土弹性模量为3.45×107kN/m2；桥墩采用圆端形截面，截面积15.47 m2，纵向抗弯惯性矩10.28 m4，墩身混凝土弹性模量为3.15×107kN/m2，桥墩高度20 m。采用ANSYS软件建立全桥有限元模型进行地震反应分析，梁和墩均采用beam3单元模拟(输入箱梁及桥墩材料、截面特性)，固定支座及活动支座采用耦合命令模拟，MTC装置采用combine40和link1单元组合模拟，其中，弹簧单元模拟装置的阻尼特性与刚度特性根据装置材料及尺寸，阻尼系数为2 000 N·s/m，连杆单元为辅助单元，通过对其应用“生死单元法”以控制装置在地震作用下的激活，分析时未考虑桩土效应，故桥墩与地面按固接处理，假定梁、墩处于弹性范围内，以便于分析MTC装置对桥梁的减震效果。

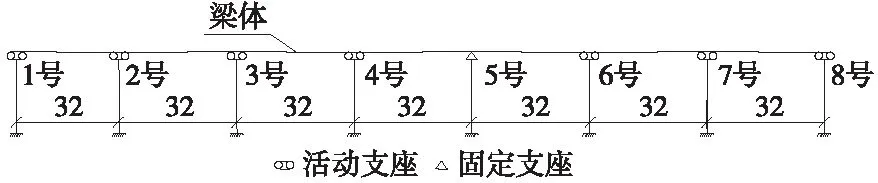
图3 连续梁桥跨布置示意(单位：m)

采用表1所示工况，以便分析装置减震效果。工况1为原桥模型，即5号墩设固定支座，其他墩纵向均设滑动支座；工况2～工况13为设置MTC装置的模型，即按相应布设方案在2号、3号、4号、6号、7号活动墩墩顶设置MTC装置。以减震率λ表示MTC装置对固定墩的减震效果，为

(15)

式中，Rmax，1为工况1最大地震响应参数；Rmax，i为工况i(i=2～13)最大地震响应参数。

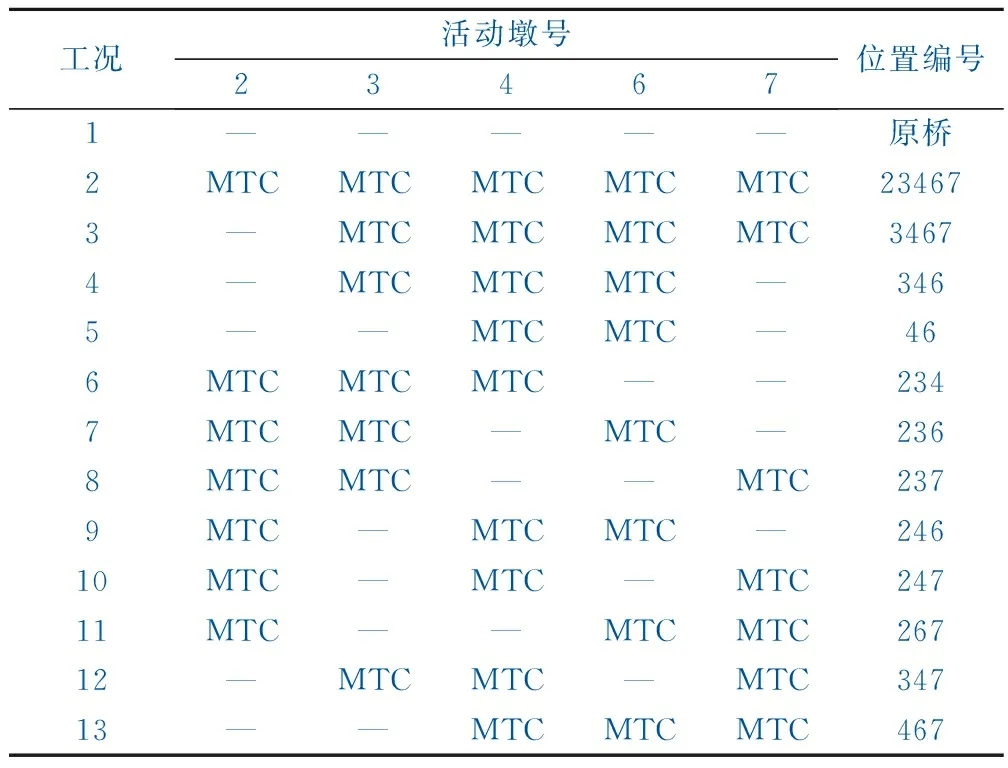
表1 MTC装置布设方案

为探究MTC装置减震适用性，在四类场地条件中各取5条地震波顺桥向输入。图4所示为20条地震波的加速度反应谱，所选地震波种类丰富，可模拟较为普遍的地震状况。

图4 加速度反应谱

4 布设方案对MTC装置减震影响

4.1 布设位置影响

为探究在小跨铁路连续梁桥上应用时，不同布设位置下MTC装置的减震情况，以表1所示布设数目为3时的9种布设方案(工况6～工况13+工况4)为分析对象，为保证不同布设位置下MTC装置介入相同的刚度值，以桥墩抗侧移刚度为基准，以η1、η2分别表示Ⅰ区限位刚度与活动墩抗侧移刚度比、Ⅱ区限位刚度与Ⅰ区限位刚度之比，本节中将η1设为4，η2设为8，Ⅰ区激活间隙设为0.015 m，Ⅱ区激活间隙设为0.02 m，地震波峰值加速度调至0.3g。图5给出20条波输入下固定墩墩底剪力、弯矩及梁端位移减震率均值。

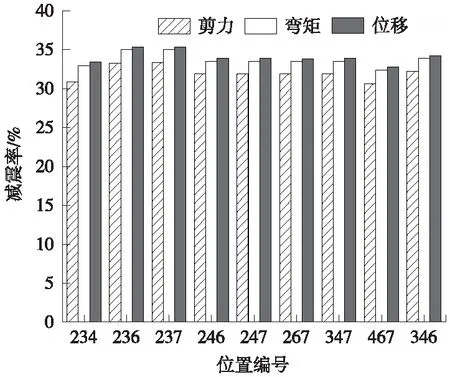
图5 MTC装置不同布设位置下减震率

由图5可得如下结论。

(1)9种布设位置下固定墩剪力、弯矩及梁端位移减震率均在30%以上，说明MTC装置具有较强的适用性，在不同布设位置均可有效提高铁路连续梁桥的抗震性能。

(2)各种固定布设位置下固定墩剪力、弯矩及梁端位移减震率略有差别，说明MTC装置的应用不但可降低固定墩发生弯剪破坏的可能性，而且能够有效地减小梁体纵向位移，起到保护支座和伸缩缝的作用。

(3)距固定墩较远的布设方案(236、237号)减震效果稍好于紧邻固定墩的布设方案(467、346、267、234号)，但整体而言，9种布设位置下的减震率数值相差不大，固定墩剪力、弯矩及梁端位移减震率极差分别为2.72%、2.64%、2.59%。说明MTC装置在中小跨铁路连续梁桥上应用时，布设位置对其减震效果的影响极小，实际应用时可将装置布设在距固定墩较远位置，以取得最优效果。

为探究不同布设位置，MTC装置激活后对桥梁整体地震响应的影响，表2给出连续梁桥各墩底剪力、弯矩极值之和及主振型所对应的自振周期。

表2 桥梁整体地震响应及自振周期

由表2可得如下结论。

(1)地震力作用下，安装MTC装置连续梁桥的剪力、弯矩响应明显大于未安装MTC装置连续梁桥。其原因在于，MTC装置发挥作用后增大了连续梁桥纵向刚度，缩短了桥梁自振周期，与原桥结构相比，增大了对应的反应谱谱值，进而导致整桥地震响应增大。

(2)9种布设位置下，连续梁桥自振周期基本相等；剪力响应在19.897×103～20.320×103kN内变化，弯矩响应在35.664×104～36.672×104kN·m内变化，变化范围极小，说明MTC装置布设数目一定时，布设位置变化对中小跨铁路连续梁桥整体地震响应基本无影响。

为验证上述结论的合理性及有限元模型的可靠性，以墩底剪力为例，基于前述理论分析进行验证。鉴于所述7跨铁路连续梁桥在9种工况下MTC装置布设数目均为3，即N=3；各桥墩截面性质相同，抗侧移刚度均以kpier表示，即kpier，i=kpier，kfix=kpier；各活动墩上MTC装置刚度设置相同，均以kMTC表示，即kMTC，i=kMTC，设工况j下连续梁桥自振周期对应的谱绝对加速度为Spa，j，将各参数代入式(8)、式(13)、式(14)，整理得工况j下的剪力响应情况为

Qmax=mSpa，j

(16)

(17)

(18)

由式(16)～式(18)可知，决定该铁路连续梁桥整体及各墩地震响应变量为地震波谱绝对加速度Spa，j，同一条地震波输入下，其值由结构自振周期确定。由表2可知，MTC装置布设数目相同时，不同布设位置下的连续梁桥自振周期基本相等，因此，不同布设位置下桥梁整体地震响应及固定墩减震率理论上相差极小。数值模拟得到的结果与这一结论相符，证明了用本文所建立的有限元模型进行MTC装置减震分析切实可行。

4.2 布设数目影响

由式(13)、式(14)可知，MTC装置布设数目不同时，地震作用下参与抵抗水平地震力的活动墩数目不同，故介入总刚度不同，减震效果将有较大差别，因此，有必要对不同布设数目下MTC装置减震效果进行探究。

鉴于MTC装置刚度分区设置以适应不同地震动情况下的减震需求，首先分析中小震下仅Ⅰ区限位装置参与减震时布设数目的影响情况。分析时地震波峰值加速度调至0.1g，以模拟中小震作用，装置Ⅰ区激活间隙设为0.015 m，Ⅱ区激活间隙设一较大值以保证其不参与减震。图6给出Ⅰ区不同限位刚度情况下，连续梁桥固定墩剪力、弯矩及梁端位移减震率三者均值与MTC装置布设数目关系曲线(各地震波下均值)。

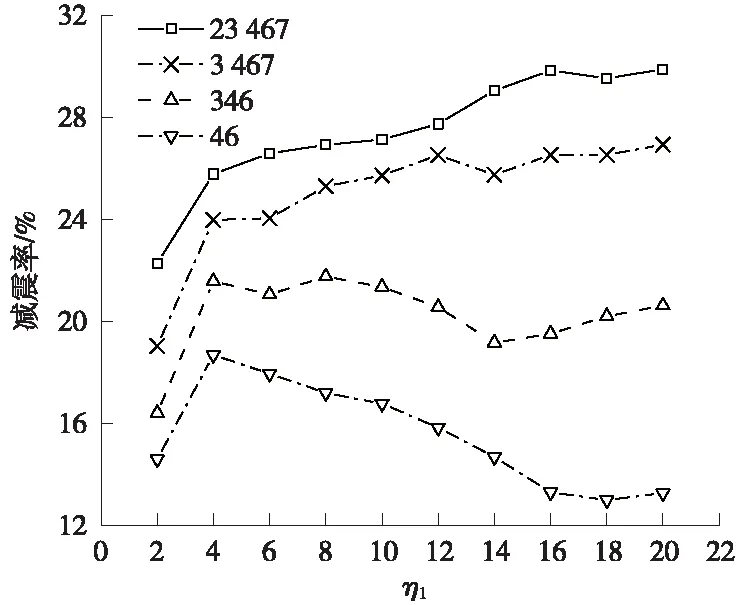
图6 PGA=0.1g减震效果

由图6可得如下结论。

(1)同一限位刚度时，布设数目越多，MTC装置减震效果越好；但不同限位刚度取值时，布设数目对减震效果的影响差别较大，介入刚度较小时，4种布设数目间减震率离散程度较小，随着介入刚度增大，4种布设数目间的减震率离散程度增加，如η1=2时，减震率极差为7.679%，η1=20时达到16.612%。说明Ⅰ区限位刚度设置较大时，减震效果对MTC装置布设数目变化更加敏感。

(2)MTC布设数目较少时，减震率随刚度增加呈先升后降趋势；布设数目较多时，减震率随刚度增加呈递增趋势，说明布设数目对Ⅰ区限位刚度取值范围有较大影响，布设数目较少时，需较为精确地控制MTC刚度，对于抗震设计略有不便。

为探究地震力进一步增大作用下，Ⅰ、Ⅱ区限位装置同时参与减震时，布设数目对MTC装置减震效果影响，取中小震作用下能较充分发挥减震效果的刚度比η1=4并保持不变，改变η2观察MTC装置减震效果。分析时地震波峰值加速度调至0.3g，以模拟地震力进一步增大情况，Ⅰ、Ⅱ区激活间隙分别设为0.015 m和0.02 m。图7给出Ⅱ区不同限位刚度情况下，减震率与布设数目关系曲线。

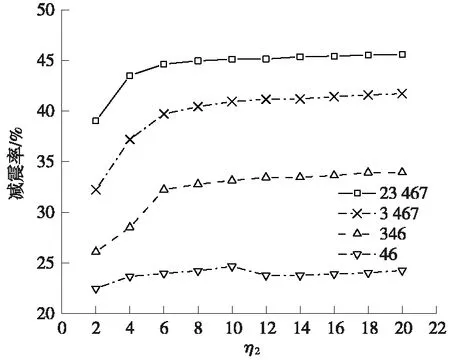
图7 PGA=0.3g减震效果

分析图7可得如下结论。

(1)不同刚度设置情况下，减震效果均随着MTC布设数目的增多而加大，说明MTC装置增多有助于降低大震下固定墩地震响应和梁端位移。

(2)MTC装置布设数目取不同值时，其减震效果受Ⅱ区限位刚度影响较小，初期随η2增加出现小幅增大，后期基本保持稳定状态，说明Ⅱ区限位刚度取值较为宽泛。

(3)综合图6、图7可知，MTC装置介入刚度之和相同时，布设数目较多时减震效果优于布设数目较少时的减震效果。如布设数目为2，η1=4时，减震率为18.691%；布设数目为4，η1=2时，减震率为19.032%。其原因在于固定墩地震响应由各活动墩刚度kpier，i、固定墩刚度kfix、MTC装置介入刚度kMTC，i和谱绝对加速度Spa决定，在中小跨铁路连续梁桥中，MTC装置介入总刚度相同情况下，布设数目较少时固定墩分配到的水平地震力更多。说明实际工程中总刚度设置相同时，将刚度分散设置到更多MTC装置上，可起到更优减震效果。

(4)结合图6、图7分析结果可见，由于MTC装置布设数目较少时减震率整体较低，且对Ⅰ区限位刚度取值范围要求较为苛刻，故建议中小跨度连续梁桥应用MTC装置减震时，其布设数目不宜小于n/2(n为活动墩数量)。如对本文连续梁桥而言，布设数目为4、5时，中小震下可普遍取得20%以上减震率，地震力进一步增大作用下可取得35%以上减震率，均起到较优减震效果，且刚度取值范围较为宽泛。

MTC装置的应用增大了活动墩受力，激发了活动墩抗震潜能，但是布设不当还可能增大连续梁桥整体地震响应，因此，除固定墩减震效果，MTC装置对桥梁整体地震响应的影响同样需要关注。由理论分析可知，整体地震响应受地震波频谱特性影响较大。此处选取3种典型地震波：LIVERMORE波、ELCENTRO波和EMC_FAIRVIEWAVE_90_w波进行仿真分析，探析布设数目对桥梁整体地震响应的影响，分析时取η1=4，η2=8，PGA=0.3g。表3给出3条地震波输入下桥梁固定墩与活动墩墩底剪力、弯矩极值之和。

由表3可知，LIVERMORE波、ELCENTRO波、EMC_FAIRVIEWAVE_90_w波输入下，随着MTC装置布设数目增多，连续梁桥整体剪力、弯矩响应分别呈递减、递增、先减后增的变化趋势。由前述理论分析中式(13)、式(14)可知，其原因在于，布设数目的增多增大了连续梁桥纵向刚度，缩短了桥梁自振周期，自振周期对应的地震波反应谱谱值也发生变化。若连续梁桥MTC减震体系的周期变化区间恰好处于地震波反应谱的单调变化区段，则体系整体地震响应呈递增/减趋势(如本例中LIVERMORE波、ELCENTRO波)；若周期变化区间处于反应谱剧烈震荡阶段，则续梁桥MTC减震体系整体地震响应随MTC装置数目变化规律性不强(如本例中EMC_FAIRVIEWAVE_90_w波)。说明MTC装置布设数目增多并非一定增大连续梁桥整体地震响应，具体影响情况与地震波频谱特性相关。

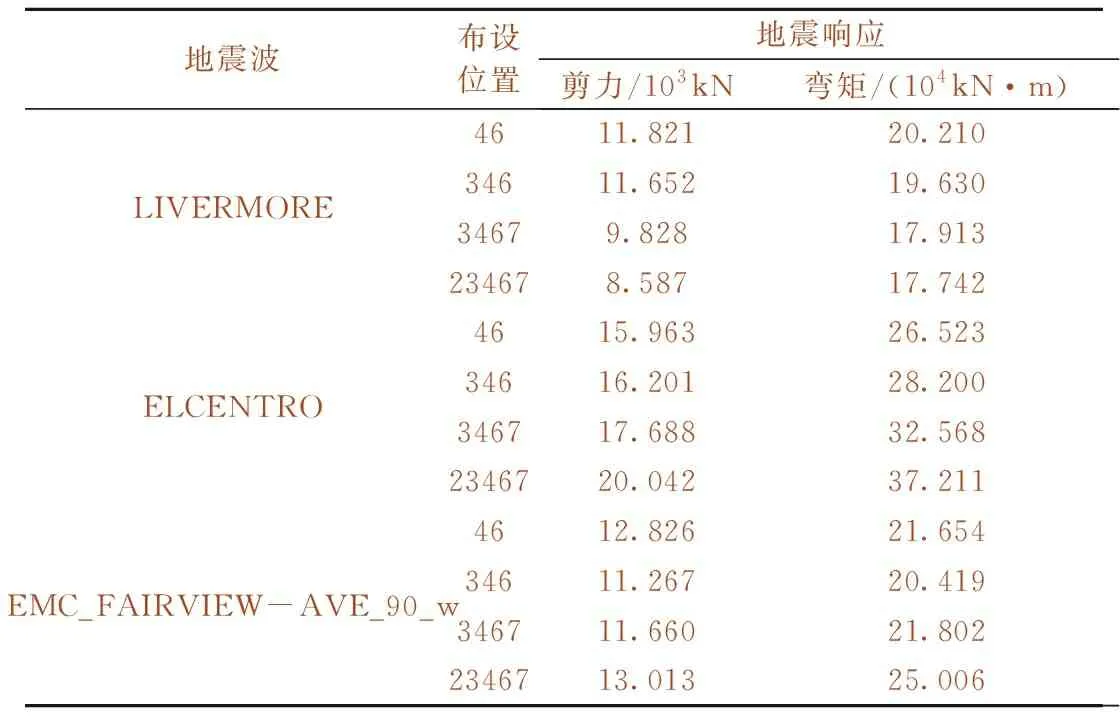
表3 不同布设数目下桥梁整体地震响应

5 布设方案综合对比

由前述分析可知，MTC装置在中小跨铁路连续梁桥上应用时，布设位置对其减震效果及连续梁桥整体地震响应影响极小，故此处采用雷达图分析法开展不同布设数目下装置减震性能综合对比。取4种布设数目下均可充分发挥较优减震效果的刚度比：仅Ⅰ区限位装置激活(地震波峰值加速度0.1g)时，η1=4、η2=0；Ⅰ、Ⅱ区限位装置共同作用(地震波峰值加速度0.3g)时，η1=4、η2=8。综合评判指标中应包含连续梁桥固定墩地震响应、活动墩地震响应及桥梁整体地震响应情况，故选取各布设方案所对应的固定墩墩底剪力、弯矩，梁端位移响应，4号活动墩墩底剪力、弯矩响应及各墩总剪力、弯矩响应作为MTC装置减震效果综合评判指标，并按相应响应最大值进行归一化处理，得到图8所示4种布设数目下结构响应雷达图。图中，越接近“1”表示地震响应越大，越接近“0”则响应越小。

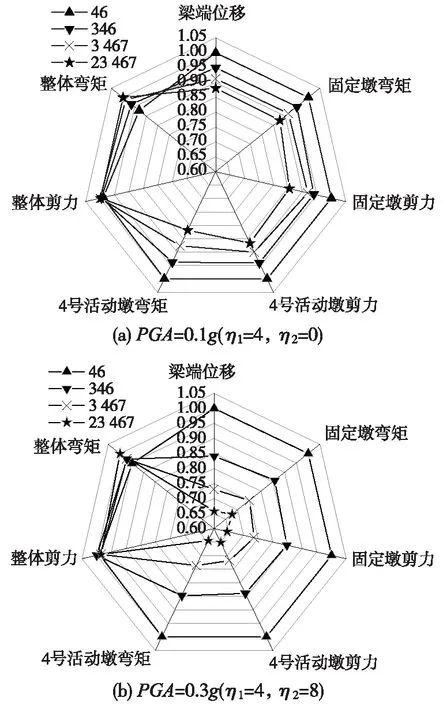
图8 结构响应雷达图

由图8可得如下结论。

(1)无论中小震还是大震作用下，布设数目越多，固定墩剪力、弯矩、梁端位移响应越小，即MTC装置减震效果越好。

(2)按最大值归一化处理后，与其他评判指标相比，不同布设数目下整体剪力、弯矩响应更为接近，因此，选择MTC装置布设数目时可将桥梁整体地震响应作为次要评判指标进行参考。

(3)对于单个活动墩而言，布设数目越多，地震响应越小(如4号活动墩)，其原因是布设数目增多使更多活动墩参与抵抗水平地震力，分配至单个活动墩的地震力有所降低。说明适当增加布设数目，可在取得更好减震效果的同时降低单个活动墩地震响应。

(4)两种峰值加速度下，布设数目为4、5时雷达图面积较小，即在未过多增大桥梁整体响应及单个活动墩受力情况下实现了较好减震效果。进一步说明MTC装置布设数目大于活动墩数目的1/2时，可取得更好的综合效果。

6 结论

(1)在中小跨铁路连续梁桥上设置MTC装置后，可根据地震力大小实现分级减震，一定程度上降低固定墩剪力、弯矩和梁端位移，取得一定减震效果，但减震效果受装置布设方案影响，实际工程中应注意选择合理的MTC装置布设数目及布设位置。

(2)MTC装置应用于中小跨度铁路连续梁桥且布设数目一定时，布设位置对减震效果及桥梁整体地震响应影响较小，为获得最佳减震效果，应尽量在距固定墩较远的活动墩上布设MTC装置。

(3)MTC装置在中小跨铁路连续梁桥上应用时，布设数目较多时减震效果普遍较好，但考虑不过多增大单个活动墩受力及桥梁整体地震响应，建议布设数目大于活动墩数目的1/2，以取得较优减震效果。

(4)布设数目变化对连续梁桥整体地震响应有所影响，影响情况与地震波频谱特性相关。