高速铁路桥梁断轨力取值方法研究
韩 冰,杨海涛,韩 旭,解会兵
(1.北京交通大学土木建筑工程学院,北京 100044; 2.交通基础设施安全与风险管理国家重点实验室,北京 100044)
引言
为保证行车舒适性,降低养护及维修成本[1],无缝线路被广泛应用于高速铁路的工程实践之中。由于无缝线路铺设时将长轨焊接,所以,无缝线路固定区在受到温度变化时,钢轨由于不能自由释放温度力,从而导致钢轨温度力较大。在寒冷季节,无缝线路固定区桥上钢轨会在薄弱环节因降温作用发生折断现象[2],由此便产生了断轨力。这会使得原本钢轨中的温度拉应力在断轨处释放,但是,扣件和轨道板结构的纵向阻力和未折断钢轨均会限制钢轨位移。断轨力产生后会经由扣件、轨枕、轨道板、砂浆层、底座板、梁体、支座传递给墩台,进而对墩台安全造成隐患。所以在铁路无缝线路桥梁墩台设计中,断轨力作为桥梁墩台特殊荷载进行设计[3]。目前,桥上断轨力的计算方法普遍基于梁轨纵向相互作用理论[4-5],张鹏飞[6]详细介绍了不同构件的单元及参数选取,建立了桥上无砟轨道无缝线路精细化模型,并提出在特定计算中可适当简化现有变截面连续梁模型[7-8]。王伟华[9]研究了线路阻力对无缝线路纵向受力的影响。张鹏飞等[10]通过建立空间模型,研究了温度荷载对特殊桥型的受力影响。刘成等[11]通过建立整桥模型,研究了梁-轨相互作用的规律。
除采用上述静力方法以外,能量法[12]在20世纪50年代也被提出并用于结构分析。从能量耗散的角度,可以将能耗分为弹性变形能、塑性耗能、阻尼耗能和结构动能。对于扣件而言,减震橡胶主要提供弹性和阻尼[13]的作用,已有学者通过冲击试验,研究了橡胶材料耗能特性在振动频率因素下的变化[14]。王书卫[15]通过试验分析了扣件中橡胶的动力性能,最终得到了频率和振幅对减振橡胶的耗能特性的影响规律。陈兆林等[16]提出了能量有限元法计算结构高频冲击响应。李爱群等[17]分析了支座阻尼器的耗能特性,为支座阻尼设置提供了一定的理论依据。
我国TB10015—2012《铁路无缝线路设计规范》规定,桥梁墩台设计中同一钢轨的伸缩力、挠曲力和断轨力不应相互组合,当断轨力大于伸缩力及挠曲力时,断轨力将对桥梁的设计起着控制作用。规范从线路阻力的角度出发进行设计,而未考虑其他因素对断轨附加力的影响,导致计算结果偏大[2]。尤其在城际铁路桥梁中,其承受的荷载与高速铁路相比较小,导致桥上挠曲力和伸缩力较小。由于在城际铁路中,断轨力对墩台设计起控制作用,因此基于现有规范计算得出的墩台设计尺寸过大,从而影响了桥梁的经济性。针对上述问题,分别以桥上无缝线路梁-轨相互作用模型和考虑结构耗能的瞬态计算模型为基础,对高铁桥梁中的线路断轨力和墩台断轨附加力的合理取值开展了研究。
1 参数选取和模型建立
1.1 计算模型
根据桥上无缝线路的结构组成形式,建立三维空间ANSYS有限元模型。其中钢轨采用60kg/m钢轨,用BEAM188梁单元模拟;扣件纵向非线性阻力采用COMBINE39非线性弹簧单元模拟,扣件纵向阻力选取24 kN/m/轨;扣件系统横向和垂向刚度采用线性弹簧单元COMBINE14模拟,刚度取200 kN/mm;轨道板、砂浆层、底座板、梁体和墩台均采用SOLID65实体单元进行模拟;滑动层由“两布一膜”组成,采取COMBIN39非线性弹簧进行模拟。
1.2 阻力计算模型
(1)扣件阻力
常见的扣件阻力模型有常量阻力模型、线性阻力模型和非线性阻力模型,其中非线性阻力模型包括指数型阻力模型和弹塑性阻力模型。其中理想弹塑性阻力模型具有计算较为便捷和计算结果在可接受的误差范围内而被广泛采用,在理想弹塑性模型中,在一定的轨道桥梁相对位移范围内,纵向阻力呈正比函数增长,当超过此位移限值后,纵向阻力不再发生变化。因此,本文采用理想弹塑性阻力模型。
(2)活动支座摩阻力
活动支座对桥梁的纵向受力和变形总是有一定的约束作用[18-19]。考虑支座摩阻率对计算结果准确性的影响和温度对活动支座摩阻率的影响,根据我国规范[3],结合本文温度工况综合分析,取活动支座摩阻率为3%。
2 计算分析
2.1 模型验证
为验证所提出的计算模型的准确性,分别将简支梁桥和连续梁桥两种桥型下断轨后钢轨纵向位移的有限元结果与既有文献[20]的数值仿真结果进行对比。孔径设置与文献[20]一致,采用5×32 m简支梁和32 m+(32+48+32) m+32 m连续梁。
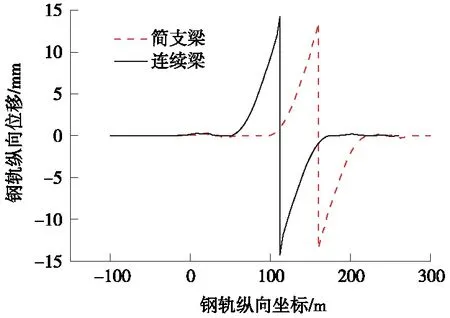
图1 钢轨与轨道板相对位移
基于1.1节介绍的仿真模型,当梁端发生断轨后,两种桥型的钢轨与轨道板相对位移的分布见图1,图中以左侧桥台位置为0坐标位置处,向小桩号侧为正,向大桩号侧为负。将计算结果汇总并与文献计算结果进行对比,对比结果列于表1。

表1 本文仿真模型与文献[20]模型的计算结果对比
由表1可知,基于提出的有限元模型计算得出的简支梁和连续梁结构断轨侧钢轨与轨道板相对位移断缝值与文献[20]模型的对应结果的百分比误差分别为1.38%和1.19%,可认为本文计算模型对于简支梁桥和连续梁桥上部无缝线路空间模型的模拟具有较高准确性。
为节约计算成本,后续分析中仅采用文献[20]中两种桥型的中间三孔进行数值分析,即采用3×32 m简支梁桥和(32+48+32) m连续梁桥进行有限元仿真计算,并对两种桥型下的温度力和断轨力进行分析,连续梁桥有限元模型如图2所示。

图2 (32+48+32) m连续梁有限元模型
2.2 基于能量耗散法则的瞬态分析结果
考虑断轨发生的瞬时性,传递路径上存在系统阻尼,以及可能导致传力构件的变形及损坏,采用瞬态分析的方法进行模拟分析。在瞬态分析中采用完全法进行计算,完全法可以考虑结构阻尼的影响并且可以添加温度应力。
温度变化是造成钢轨折断产生断轨力的直接原因,主要考虑以下3个温度工况。
(1)工况1:降温30 ℃;
(2)工况2:降温40 ℃;
(3)工况3:降温50 ℃。
不同温度下发生断轨的瞬态计算简支梁结果见图3~图5及表2。

图3 工况1简支梁钢轨温度力
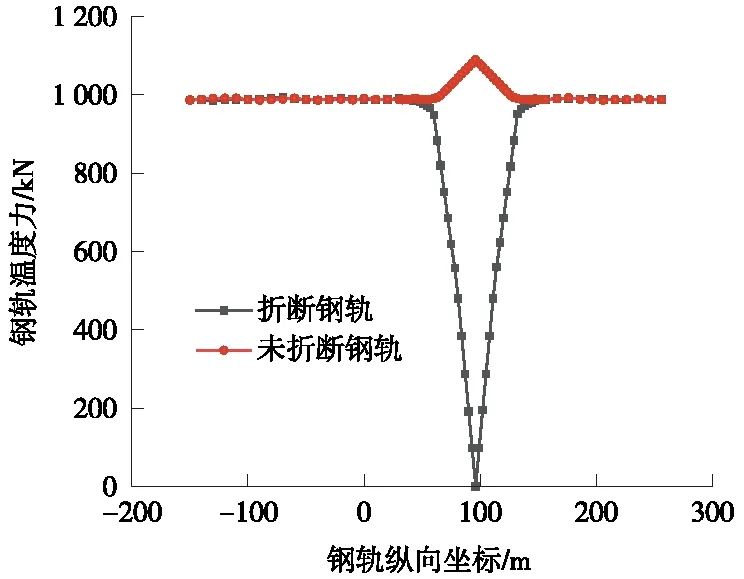
图4 工况2简支梁钢轨温度力

图5 工况3简支梁钢轨温度力
由图3~图5分析可知,当其他影响因素保持一致时,在简支梁桥上无缝线路断轨力及其对墩台的传递瞬态分析计算中,温度对简支梁桥上无缝线路断轨力的影响规律为,在一定范围内,钢轨温度降温幅度越大,钢轨温度力就越大。未发生断轨时,当钢轨温度降低30 ℃时,钢轨最大温度力为654.27 kN;当钢轨温度降低40 ℃时,钢轨最大温度力为828.06 kN,相比钢轨温度降温30 ℃变大了173.79 kN,变化幅度为26.56%;当钢轨温度降低50 ℃时,钢轨最大温度力为983.62 kN,相比钢轨温度降温40 ℃变大了155.56 kN,变化幅度为18.79%。断轨发生后,当钢轨温度降低30 ℃时,断轨侧钢轨最大温度力为653.12 kN,对比断轨前变化了-1.15 kN,变化幅度为-0.18%;未断轨侧钢轨最大温度力为745.36 kN,对比断轨前增大了91.09 kN,增大幅度为13.92%。当钢轨温度降低40 ℃时,断轨侧钢轨最大温度力为828.03 kN,对比断轨前变化了-1.03 kN,变化幅度为-0.12%;未断轨侧钢轨最大温度力为940.25 kN,对比断轨前增大了112.19 kN,增大幅度为13.55%。当钢轨温度降低50 ℃时,断轨侧钢轨最大温度力为982.16 kN,对比断轨前变化了-1.46 kN,变化幅度为-0.15%;未断轨侧钢轨最大温度力为1 090.17 kN,对比断轨前增大了106.55 kN,增大幅度为10.83%。
对比分析可得,工况2与工况1对比,断轨侧钢轨温度力增大了173.91 kN,增大幅度为26.63%,未断轨侧钢轨温度力增大了194.89 kN,增大幅度为26.15%;工况3与工况2对比,断轨侧钢轨温度力增大了155.13 kN,增大幅度为18.76%,未断轨侧钢轨温度力增大了149.92 kN,增大幅度为15.94%。

表2 温度变化时简支梁计算结果对比
由表2分析可得,当发生断轨后,简支梁桥上的无缝线路墩台断轨附加力与温度变化之间的关系为:随着温度降温幅度的增大,桥墩断轨附加力也会逐渐增大。当温度降温幅度为30 ℃时,桥墩断轨附加力最大值为205.99 kN;当温度降温幅度为40 ℃时,桥墩断轨附加力最大值为233.10 kN,对比温度降温幅度为30 ℃时,桥墩断轨附加力增大了27.11 kN,增大幅度为13.16%;当温度降温幅度为50 ℃时,桥墩断轨附加力最大值为262.13 kN,对比温度降温幅度为40 ℃时,桥墩断轨附加力增大了29.03 kN,增大幅度为12.45%。
不同温度下发生断轨的瞬态计算连续梁结果见图6~图8及表3。
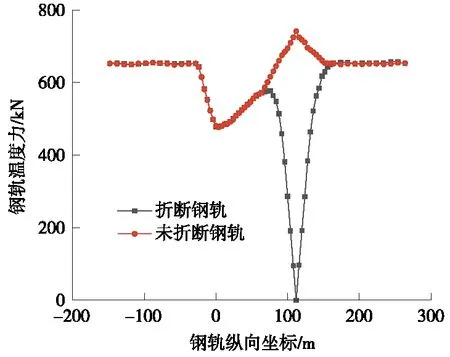
图6 工况1连续梁钢轨温度力
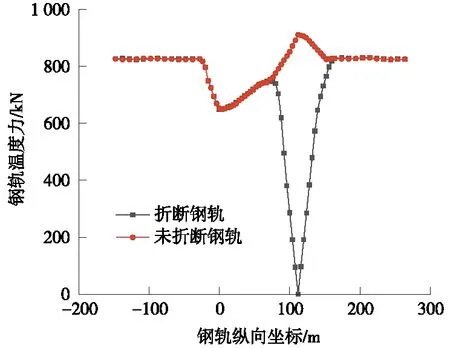
图7 工况2连续梁钢轨温度力

表3 温度变化时连续梁计算结果对比
由图6~图8及表3计算结果可得,连续梁断轨力变化规律与简支梁基本一致,不同的是桥墩断轨附加力较简支梁大,这是由于连续梁桥墩为固定支座,刚度较大。当降温幅度为30 ℃时,桥墩断轨附加力最大值为575.00 kN;当降温幅度为40 ℃时,桥墩断轨附加力最大值为644.83 kN,对比温度降温幅度为30 ℃时,桥墩断轨附加力增大69.83 kN,增大幅度为12.14%;当降温幅度为50 ℃时,桥墩断轨附加力最大值为691.05 kN,对比温度降温幅度为40 ℃时,桥墩断轨附加力增大了46.22 kN,增大幅度为7.16%。并且桥墩断轨附加力最大值均出现在固定支座桥墩位置处。
3 计算结果对比
3.1 简支梁计算结果对比
简支梁桥桥墩断轨附加力规范取值与按照静力分析方法的取值对比见表4,由对比结果可得:静力计算结果明显小于规范取值,且减小幅度较大。这是由于规范取值考虑因素过于单一,仅考虑了线路阻力的影响,并且未考虑简支梁墩台受力的不同,当断轨时,简支梁桥台断轨附加力较大,而桥墩受力较小,因此可以认为规范中对于桥墩断轨附加力的取值偏于保守。

表4 简支梁桥墩台断轨附加力对比
在不同降温幅度下,基于静力分析和瞬态分析两种方法得到的简支梁桥桥墩断轨附加力的取值对比见表5,由对比结果可得:基于瞬态分析方法的取值结果要小于采用静力分析的取值结果,其降低幅度在14%左右。这是由于瞬态分析能够考虑能量在传递路径中的损耗,因此可以认为基于能量耗散的断轨力计算方法指导设计更为经济。

表5 基于静力分析方法和瞬态分析方法的简支梁桥桥墩断轨附加力取值对比
3.2 连续梁计算结果对比
连续梁桥桥墩断轨附加力规范取值与静力分析取值对比见表6,由对比结果可得:静力计算结果明显小于规范取值,规律与简支梁情况一致。

表6 连续梁桥桥墩台断轨附加力对比
类似地,基于前述两种分析方法得到的连续梁桥桥墩断轨附加力的取值对比见表7,由对比结果可得:基于瞬态分析的取值结果要小于基于静力分析方法的结果,降低幅度在17%左右。

表7 基于静力分析方法和瞬态分析方法的连续梁桥桥墩断轨附加力取值对比
4 结论
考虑断轨力自产生到传递给墩台顶为一瞬态过程,在传递路径中会存在能量的转换与消耗,传统计算方法基于梁-轨相互作用得出的断轨力误差较大。本文考虑了断轨的瞬时特征,建立了瞬态计算的分析模型,最终给出断轨力及断轨附加力的合理取值方法。主要结论如下。
(1)断轨发生后,钢轨温度力整体变化趋势如下:断轨侧钢轨在断轨位置处温度力变为0;未断轨侧钢轨在断轨位置处,钢轨温度力会明显增大。
(2)断轨发生后,降温幅度会对断轨力和墩台断轨附加力均有较为显著的影响,随着降温幅度的增大,断轨力和墩台断轨附加力均会随之增大,但是增大幅度呈减缓趋势。
(3)对比规范墩台断轨附加力和梁-轨相互作用的取值可以得到:规范取值仅从线路阻力计算,未考虑不同墩台受力的不同,尤其在简支梁中,桥台断轨附加力较大,而桥墩受力较小,因此可以认为规范中对于桥墩断轨附加力的取值偏于保守。
(4)对比墩台断轨附加力瞬态分析和静力分析计算结果可以得到:瞬态分析考虑结构耗能后会减小未断轨侧钢轨温度力最值和墩台承受的断轨附加力,且简支梁桥墩台断轨附加力减小幅度为13%~15%,连续梁桥墩台断轨附加力减小幅度为16%~19%。

