Symmetry Tense Heyting Algebras

Xue Ge

Abstract.In this paper we introduce the class of symmetry tense Heyting algebras (sIK.talgebras),which is a S4 extension of Ewald’s intuitionistic tense logic.We present the Hilbert axiomatization for sIK.t.Further we show the finite model property(FMP)for the logic of sIK.talgebras.The result is proved by proof theory and algebraic model theory,using the sequent systems introduced by the present paper.

1 Introduction

Intuitionistic tense logic(IK.t),as a special class of intuitionistic modal logics,has been introduced by Ewald in[5].It is obtained by extending intuitionistic logic with two pairs of adjoint modalities(F(♢),H(■))and(P(♦),G(□)).In[5],Ewald gave the Kripke models of the logic,and gave the axiomatizations of the intuitionistic modal logics corresponding to various conditions on the temporal ordering and proved the appropriate completeness results.Algebraic semantics for IK.t was given by Figallo and Pelaitay in[6],which is Heyting algebras with 4 modal operators satisfying the following conditions:

(t1) □1=1 and ■1=1;

(t2) □(a∧b)=□a∧□band ■(a∧b)=■a∧■b;

(t3)a ≤■♢aanda ≤□♦a;

(t4) ♢0=0 and ♦0=0;

(t5) ♢(a ∨b)=♢a ∨♢band ♦(a ∨b)=♦a ∨♦b;

(t6) ♢■a ≤aand ♦□a ≤a;

(t7) ♢(a→b)≤□a→♢band ♦(a→b)≤■a→♦b.

It was shown that IK.t is sound and complete with respect to the class of IK.talgebras.([6])Beyond Ewald’s setting,Chajda([3])introduced another class of basic intuitionistic tense algebras by excluding(t6)and replacing(t7)with a condition of dual of the modalities:(t8)♦a=¬■¬aand ♢a=¬□¬a.This follows the tradition of Bull’s intuitionistic modal logic.([1])However since¬¬aain Heyting algebras,(t6) is not derivable from (t8) and (t3).There is no argument of why (t6) should be excluded from tense Heyting algebras in [3].And indeed (t6) holds in different tense Heyting algebras.([6,4])Hence in the present paper we consider Chajda’s tense Heyting algebras enriched with(t6).We consider the S4 enrichment of this kind of tense Heyting algebras which is namedSymmetry Tense Heyting Algebras(sIK.t)in this paper.

Symmetry tense Heyting algebras are natural structures,which turn out to be Heyting algebras enriched with two pairs of adjoint modalities (F(♢),H(■)) and(P(♦),G(□))satisfying the following Galois,De Morgan connections:

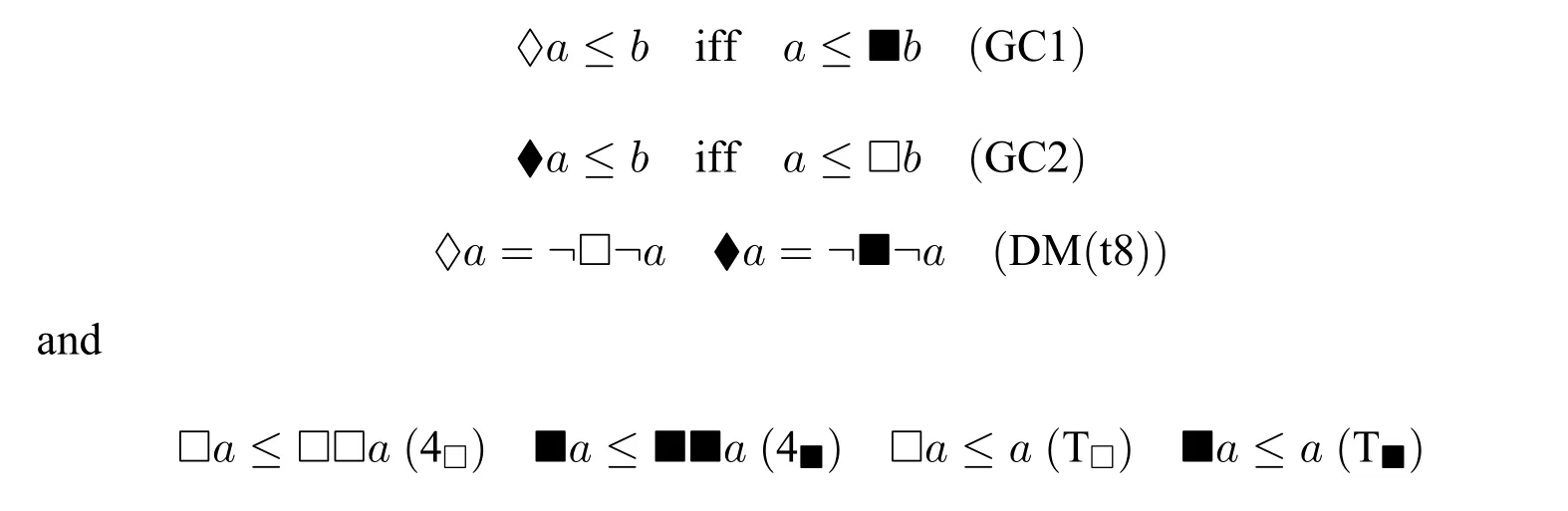
Clearly sIK.t-algebras are extensions of H2GC algebras discussed in[4].In[2],intuitionistic logic with independent pairs ofn-ary Galois connections are introduced by W.Buszkowski,and the strong finite model property(SFMP)of this logic is proved in the same paper.The main contribution of this paper is as follows:(1)we introduce the definition of sIK.t-algebras and show that every sIK.t-algebra is an IK.t-algebra;(2)we give the Hilbert style axiomatization of sIK.t-algebras and show the soundness and completeness;(3)we prove the FMP of the logic of sIK.t-algebras.

The paper is organized as follows.In section 2,we introduce sIK.t-algebras and show their relation with IK.t-algebras.In section 3,we present the logic of sIK.talgebras via Hilbert style system and show the soundness and completeness.In last section we present a sequent system of sIK.t-algebras and prove the FMP via this sequent system.

2 Symmetry Tense Heyting Algebras

Definition 1.LetA=(A,∧,∨,→,0,1)be a Heyting algebra.Define¬a=a→0,♢a=¬□¬aand ♦a=¬■¬a,□a=¬♢¬aand ■a=¬♦¬a.♢,♦are unary operators(called tense operators)onAsatisfying the following conditions for alla,b ∈A:

(c1) □1=1 and ■1=1;

(c2) ♢(a ∨b)=♢a ∨♢band ♦(a ∨b)=♦a ∨♦b;

(c3) ♢■a ≤aand ♦□a ≤a;

(c4) □a ≤□□aand ■a ≤■■a;

(c5) □a ≤aand ■a ≤a.

The algebraic structureA=(A,∧,∨,→,0,1,♢,♦) is a symmetry tense Heyting algebra(sIK.t).

Let us consider the following example:

Figure 1 :The lattice 9

Example 1.The lattice 9 is defined as figure 1.♢,♦are defined as follows.This lattice is a sIK.t-algebra.

Lemma 1.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any ⋆∈{♢,□,♦,■}and a,b ∈A a ≤b implies ⋆a ≤⋆b.

Proof.Sincea ≤b,b=a ∨b.Then ♢b=♢(a ∨b).By Definition 1 (c2),♢(a ∨b)=♢a ∨♢b.Then ♢b=♢a ∨♢b.Hence ♢a ≤♢b.By Duality,□a ≤□b.Analogously we can prove ♦a ≤♦band ■a ≤■b. □

Lemma 2.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any ⋆∈{♢,□,♦,■}and a ∈A,¬¬⋆a=⋆a for any ⋆∈{♢,□,♦,■}.

Proof.By Definition 1,¬¬♢a=¬¬¬□¬aand ♢a=¬□¬a.Obviously in Heyting algebras¬¬¬b=¬bfor anyb ∈A.Thus¬¬¬□¬a=¬□¬a.Hence¬¬♢a=♢a.By Duality,¬¬□a=□a.Analogously we can reach¬¬♦a=♦aand¬¬■a=■a. □

Lemma 3.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any ⋆∈{♢,□,♦,■}and a ∈A,¬♢a=□¬a,¬□a=♢¬a,¬♦a=■¬a and¬■a=♦¬a.

Proof.By Definition 1,¬♢a=¬¬□¬a.Then by Lemma 2,¬¬□¬a=□¬a.Thus¬♢a=□¬a.By Duality,¬□a=♢¬a.Others can be proved similarly. □

Lemma 4.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any a ∈A the following holds:

(1) □a=□¬¬a and■a=■¬¬a;

(2) ♢a=♢¬¬a and♦a=♦¬¬a.

Proof.(1) By Lemma 3,¬♢¬a=□¬¬a.Then by Definition 1,□a=□¬¬a.Similarly we can prove ■a=■¬¬a.

(2)By Lemma 3,¬□¬a=♢¬¬a.Then by Definition 1,♢a=♢¬¬a.Similarly we can prove ♦a=♦¬¬a. □

Lemma 5.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any a ∈A a ≤□♦a and a ≤■♢a hold.

Proof.By Definition 1(c3),♢■¬a ≤¬a.By transposition,¬¬a ≤¬♢■¬a.By Lemma 3 and Definition 1,¬♢■¬a=□¬■¬a=□♦a.Thus¬¬a ≤□♦a.Sincea ≤¬¬a,a ≤□♦a.Analogously we can reach the second inequality. □

Lemma 6.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any a,b ∈A the following holds:

(1) □(a∧b)=□a∧□b and■(a∧b)=■a∧■b;

(2) □a ∨□b ≤□(a ∨b)and■a ∨■b ≤■(a ∨b);

(3) □(a→b)≤□a→□b and■(a→b)≤■a→■b.

Proof.(1)Clearly by Lemma 1,we have □(a∧b)≤□aand □(a∧b)≤□b.Thus□(a∧b)≤□a∧□b.Conversely,by Lemma 1,we have ♦(□a∧□b)≤♦□aand♦(□a∧□b)≤♦□b.Then ♦(□a∧□b)≤♦□a∧♦□b.By Definition 1(c3),we have ♦□a∧♦□b ≤a∧b.Therefore,♦(□a∧□b)≤a∧b.By Lemma 1 again,□♦(□a∧□b)≤□(a∧b).Finally by Lemma 5,we have □a∧□b ≤□♦(□a∧□b).Thus □a∧□b ≤□(a∧b).Analogously we can prove ■(a∧b)=■a∧■b.

(2)Clearly by Lemma 1,we have □a ≤□(a ∨b)and □b ≤□(a ∨b).Thus□a ∨□b ≤□(a ∨b).Analogously we can reach the second inequality.

(3)We suffice to show □a∧□(a→b)≤□b.Clearlya∧(a→b)≤b.By Lemma 1,□(a∧(a→b))≤□b.By(1),□a∧□(a→b)=□(a∧(a→b))≤□b.Hence □(a→b)≤□a→□b.Analogously we can reach the second inequality.□

Lemma 7.In a sIK.t A=(A,∧,∨,→,0,1,♢,♦),the following adjoint property holds:

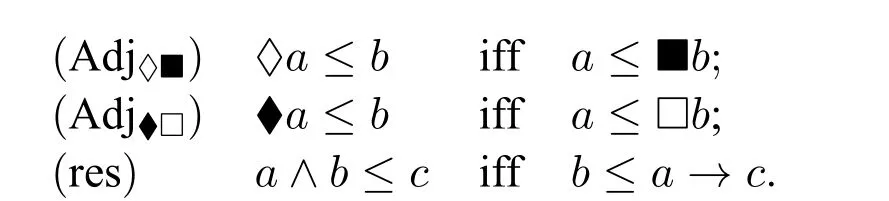
Proof.(res)is obvious.Let us show others.Assume that ♢a ≤b.By Lemma 1,■♢a ≤■b.By Lemma 5,a ≤■♢a.Thusa ≤■b.Conversely leta ≤■b.By Lemma 1,♢a ≤♢■b.By Definition 1(c3),♢■b ≤b.Thus ♢a ≤b.Analogously we can reach(Adj♦□). □

Lemma 8.Let♢,♦be unary operations over A=(A,∧,∨,→,0,1),and A be a Heyting algebra.Then Lemma 1 can be derived from(Adj♢■)and(Adj♦□).

Proof.Leta ≤b.Obviously ♢b ≤♢b.By(Adj♢■),b ≤■♢b.Soa ≤■♢b.By(Adj♢■),♢a ≤♢b.Leta ≤b.Obviously ■a ≤■a.By(Adj♢■),♢■a ≤a.So♢■a ≤b.By(Adj♢■),■a ≤■b.Others can be treated similarly. □

Lemma 9.Let♢,♦be unary operations over A=(A,∧,∨,→,0,1),and A be a Heyting algebra.Then(c1)-(c3)can be derived from(Adj♢■)and(Adj♦□).

Proof.(c1):Obviously,□1≤1 and ♦1≤1.Then by (Adj♦□),1≤□1.So 1=□1.Analogously we can prove 1=■1.

(c2):We know thata ≤a ∨bandb ≤a ∨b.By Lemma 1,♢a ≤♢(a ∨b)and ♢b ≤♢(a ∨b).So ♢a ∨♢b ≤♢(a ∨b).Conversely,♢a ≤♢a ∨♢band♢b ≤♢a∨♢b,by(Adj♢■),a ≤■(♢a∨♢b)andb ≤■(♢a∨♢b)respectively.Thusa ∨b ≤■(♢a ∨♢b).By(Adj♢■),♢(a ∨b)≤♢a ∨♢b.

(c3):We know that ■a ≤■a.By(Adj♢■),♢■a ≤a.Similarly □a ≤□a,by(Adj♦□),♦□a ≤a. □

One can present the sIK.tA by another equivalent definition.

Definition 2.A sIK.t algebra (sIK.tA) (A,∧,∨,→,0,1,♢,♦) is a structure such that(A,∧,∨,→,0,1)is a Heyting algebra and ♢,♦are unary operations onAsatisfying the following conditions for alla,b ∈A:

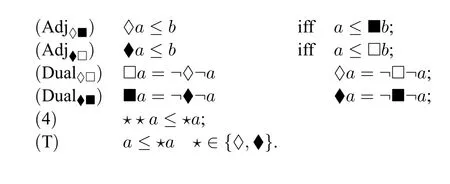
(c4)and(c5)are derived from(4)and(T)respectively.

Lemma 10.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),the following holds:

(1) ■♢■a=■a and♢■♢a=♢a;

(2) □♦□a=□a and♦□♦a=♦a.

Proof.We show(1).By Definition 1(c3),♢■a ≤a.By Lemma 1,■♢■a ≤■a.Further by Lemma 5,■a ≤■♢(■a).Thus ■♢■a=■a.By Definition 1 (c3),♢■(♢a)≤♢a.Further by Lemma 5,a ≤■♢a.By Lemma 1,♢a ≤♢■♢a.So♢■♢a=♢a.The proof for(2)is quite similar to(1). □

Lemma 11.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any a,b ∈A♢a∧b ≤0iff a∧♦b ≤0.

Proof.Let ♢a∧b ≤0.Thenb ≤¬♢a.By Lemma 3,¬♢a=□¬a.Sob ≤□¬a.Thus by Lemma 7,♦b ≤¬a.Hencea∧♦b ≤0.Conversely leta∧♦b ≤0.Thena ≤¬♦b.By Lemma 3,a ≤■¬b.Thus by Lemma 7,♢a ≤¬b.Hence ♢a∧b ≤0.□

If one replaces ♢a=¬□¬aand ♦a=¬■¬aby the following condition in the definition of sIK.t:♢(a→b)≤□a→♢band ♦(a→b)≤■a→♦b,then one obtains the IK.t.

Lemma 12.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any a,b ∈A□(a→b)≤♢a→♢b and■(a→b)≤♦a→♦b.

Proof.We know thata∧(a→b)≤b.By Fact,¬b∧a∧(a→b)≤(b∧¬b)=0.By Lemma 9,♦□(¬b∧(a→b))≤(¬b∧(a→b)).So ♦□(¬b∧(a→b))∧a ≤¬b∧a∧(a→b)≤0.By Lemma 11,□(¬b∧(a→b))∧♢a ≤0.Since□(¬b∧(a→b))=□¬b∧□(a→b),we have □¬b∧♢a∧□(a→b)≤0.Thus by(res),♢a∧□(a→b)≤¬□¬b.Hence by Definition 1,♢a∧□(a→b)≤♢b.Then by(res),□(a→b)≤♢a→♢b.Analogously we can prove ■(a→b)≤♦a→♦b.□

Lemma 13.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any a,b,c ∈A the following holds:

(1)If♢(♦a∧b)≤c,then a∧♢b ≤c;

(2)If♦(♢a∧b)≤c,then a∧♦b ≤c.

Proof.We provide the proof for(1).The argument for(2)is quite similar.Assume that ♢(♦a∧b)≤c,then by(Adj♢■),one gets ♦a∧b ≤■c.By(res),♦a ≤b→■c.By(Adj♦□),a ≤□(b→■c).By Lemma 12,a ≤♢b→♢■c.Since ■c ≤■c,by(Adj♢■),one obtains ♢■c ≤c.Thus ♢b→♢■c ≤♢b→c.Hencea ≤♢b→c.By(res),a∧♢b ≤c. □

Lemma 14.In a sIK.tA(A,∧,∨,→,0,1,♢,♦),for any a,b,c ∈A♢(a→b)≤□a→♢b and♦(a→b)≤■a→♦b.

Proof.By Definition 1 (c3),♦□a ≤a.Then by Fact,♦□a∧(a→b)≤a∧(a→b).Further sincea∧(a→b)≤b,♦□a∧(a→b)≤b.By Lemma 1,♢(♦□a∧(a→b))≤♢b.By Lemma 13(1),□a∧♢(a→b)≤♢b.Thus by(res),♢(a→b)≤□a→♢b.Analogously we can prove ♦(a→b)≤■a→♦b. □

Clearly any sIK.t-algebra is a S4 extension of Ewald’s IK.t-algebras in[6].

Lemma 15.Any sIK.t-algebras are S4 IK.t-algebras.

3 Axiomatization

In this section we shall present the Hilbert Systems corresponding to all the algebras which have been discussed in the last section.

The language ofLconsists of propositional variablesp,q,r,...,two constants⊤,⊥,four unary logical connectives ♢,♦,□and ■,three binary connectives→,∧,∨and parentheses.The formation of well formed formulae(wff)is as usual.¬is a definable connective which is defined by¬α=α→⊥.

Axiom schemes:

Now we will prove that the sIK.t-algebras are the algebraic counterparts of the sIK.t systems.Let (A,∧,∨,→,0,1,♢,♦) be a sIK.t algebra.Let Var be set of all atomic formulasp,q,r,...andμbe a mapping from Var toA.We writeμ(p)as the corresponding element ofpinA.This mapping can be extended to the set of formulasFnaturally by the following way:μ(α·β)=μ(α)·μ(β)andμ(⋆α)=⋆(μ(α))for anyα,β ∈F,· ∈{∧,∨,→}and⋆∈{♢,□,♦,■}.Note thatμ(¬α)=¬μ(α).A sIK.t algebraic model is a pair(A,μ)such that A is a sIK.t andμis a mapping from Var toA.A formula is true for(A,μ)ifμ(α)=1 in A.A formula is valid for sIK.t ifμ(α)=1 for any sIK.t model(A,μ).We writeαifαis valid for sIK.t.

Theorem 1.For any formula α,if ⊢sIK.tα,then

Proof.We proceed by induction on the length of proof ofα.We first check all formulas in axiom schemes are valid regularly.For instance let us consider ♢■α→α.Let(A,μ)be a model for sIK.t.μ(♢■α→α)=♢■(μ(α))→μ(α).It suffices to show that 1≤♢■(μ(α))→μ(α).Since by Definition 1(c3),♢■(μ(α))≤μ(α).Further 1∧♢■(μ(α))=♢■(μ(α)).Thus 1∧♢■(μ(α))≤μ(α).Hence by(res),one obtains 1≤♢■(μ(α))→μ(α).ThussIK.t♢■α→α.

Assume that⊢sIK.tαis obtained by rule (MP).Suppose that the premises are⊢sIK.tβ→αand⊢sIK.tβ.Let(A,μ)be a model for sIK.t.By induction hypothesis,(1)1≤μ(β)→μ(α)and(2)1≤μ(β)in A.Thus by(res),1∧μ(β)≤μ(α).Soμ(β)≤μ(α).Together with(2),1≤μ(α).ThussIK.tα.

Assume that⊢sIK.tαis obtained by rule(□).Suppose the premise is⊢sIK.tα′whereα=□α′.Let(A,μ)be a model for sIK.t.By induction hypothesis,1≤μ(α′)in A.By Lemma 1,□1≤□μ(α′).By Definition 1(c1),□1=1.Thus 1≤□μ(α′).SosIK.t□α′.HencesIK.tα.The proof for the case(■)is quite similar. □

Letα～β=⊢sIK.tβ→α&⊢sIK.tα→β.Clearly～is an equivalence relation,hence～is a congruence.Define sIK.t class〚α〛={β|α～β}.Let the set of all sIK.t classes be denoted byF/～.Define operations 0,1,∧′,∨′,→′,♢′,♦′onF/～as follows:

Define an order≤′onF/～:〚α〛≤′〚β〛iff〚α〛=〚α∧β〛.

Lemma 16.For any〚α〛,〚β〛∈F/～,〚α〛≤′〚β〛iff ⊢sIK.tα→β.

Proof.Let 〚α〛≤′〚β〛.So 〚α〛=〚α∧β〛.Thus⊢sIK.tα→α∧β.Clearly⊢sIK.tα∧β→β.Thus⊢sIK.tα→β.Conversely let⊢sIK.tα→β.Since⊢sIK.tα→α,⊢sIK.tα→α∧β,⊢sIK.tα∧β→α.Soα～α∧β.Hence〚α〛=〚α∧β〛.Thus〚α〛≤′〚β〛. □

Lemma 17.(F/～,0,1,∧′,∨′,→′,♢′,♦′)is a sIK.t.

Theorem 2.For any formula α,ifsIK.tα,then ⊢sIK.tα.

Proof.sIK.tα.One constructs (F/～,0,1,∧′,∨′,→′,♢′,♦′) as above.By Lemma 17,(F/～,0,1,∧′,∨′,→′,♢′,♦′)is a sIK.t.Letμbe a mapping from Var toF/～such thatμ(p)=〚p〛.By induction on the complexity of formula,one can easily prove thatμ(α)=〚α〛.Suppose thatsIK.tα.Then 1≤μ(α).So 〚⊤〛≤′〚α〛.By Lemma 16,⊢sIK.t⊤→α.Thus⊢sIK.tαwhich contradicts to assumption.HencesIK.tα.Hence ifsIK.tα,then⊢sIK.tα. □

Theorem 3.sIK.tis sound and complete with respect to sIK.t-algebra.

4 Finite Model Property

Definition 3.The set of formulas(terms)Fis defined inductively as follows:

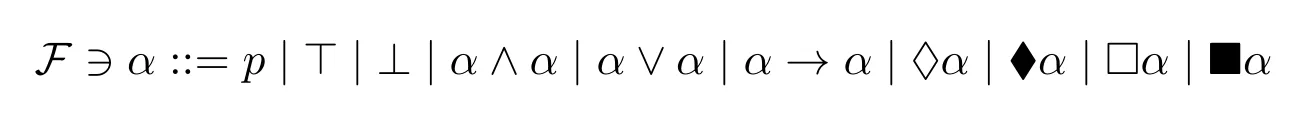
wherep ∈Var.Define¬α=α→⊥.

Definition 4.The set of all formula structuresFSis defined inductively as follows:

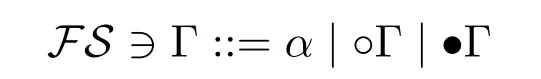
Asequentis an expression of the form Γ⇒βwhere Γ is a formula structure andβis a formula.We use the abbreviationα ⇔βforα ⇒βandβ ⇒α.We denote°n(α)=°(°n-1(α)),°0(α)=α.Acontextis a formula structure Γ(-)with a designated position(-)which can be filled with a formula structure.In particular,a single position(-)is a context.Let Γ(α)be formula structure obtained from Γ(-)by substituting formulaαfor(-).

Definition 5.The sequent calculus G for the sIK.t consists of the following axioms and rules:

(1) Axiom:

(2) Logical rules:

(3) Structural rules:

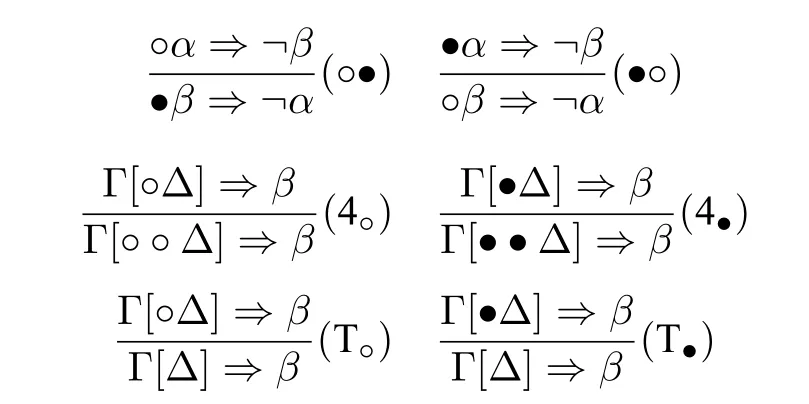
(4) Cut rule:

A sequent Γ⇒βis provable in G,notation⊢GΓ⇒β,if there is a derivation of Γ⇒βin G.We write⊢Gα ⇔βif⊢Gα ⇒βand⊢Gβ ⇒α.Note that though the cut elimination does not hold in G,another property called interpolant(see Lemma 22)holds which will play an essential role in the proof of FMP for G.

Lemma 18.The following holds inGsIK.t：

(1)¬¬⊥⇔⊥;

(2)¬(α ∨β)⇔¬α∧¬β;

(3)¬(α∧β)⇔¬(¬¬α∧¬¬β);

(4)¬(α→β)⇔¬(¬¬α→¬¬β);

(5)¬¬(α∧β)⇔¬¬(¬¬α∧¬¬β);

(6)¬¬(α→β)⇔¬¬(¬¬α→¬¬β);

(7)¬(α1∨α2)⇒¬αi(i=1,2);

(8)¬¬(¬¬α ∨¬¬β)⇔¬¬(α ∨β);

(9)¬¬(¬¬α∧¬¬β)⇔¬¬α∧¬¬β;

(10)¬¬(¬¬α→¬¬β)⇔¬¬α→¬¬β.

Lemma 19.The following holds inGsIK.t：

(1)¬(♯α∧♯β)⇔¬¬(¬♯α ∨¬♯β)♯∈{♢,♦,□,■};

(2)¬(♯α ∨♯β)⇔¬¬(¬♯α∧¬♯β)♯∈{♢,♦,□,■};

(3) ♢α ⇔¬□¬α,♦α ⇔¬■¬α;

(4) □α ⇔¬♢¬α,■α ⇔¬♦¬α.

Proof.(1) Clearly¬(¬♯α ∨¬♯β)⇔¬¬♯α∧¬¬♯β.Hence¬¬(¬♯α ∨¬♯β)⇔¬(¬¬♯α∧¬¬♯β).By Lemma 18(3),one obtains¬(♯α∧♯β)⇔¬(¬¬♯α∧¬¬♯β),whence¬(♯α∧♯β)⇔¬¬(¬♯α ∨¬♯β).

(2)Clearly¬(♯α ∨♯β)⇔¬♯α∧¬♯β.Hence¬(♯α ∨♯β)⇔¬¬¬♯α∧¬¬¬♯β.By Lemma 18(9),one obtains¬¬¬♯α∧¬¬¬♯β ⇔¬¬(¬♯α∧¬♯β),whence¬(♯α∨♯β)⇔¬¬(¬♯α∧¬♯β).

(3)Clearly by rule(□L),one obtains·□¬α ⇒¬α.Then by rule(·°),°α ⇒¬□¬α.Finally by rule (♢L),♢α ⇒¬□¬α.Conversely,since°α ⇒¬¬ ° α.Then by rule (°·),·¬ ° α ⇒¬α.Further by rule (□R) and (♢L),one obtains¬♢α ⇒□¬α.Thus¬□¬α ⇒¬¬♢α.By(¬¬),¬¬♢α ⇒♢α.Hence by(Cut),¬□¬α ⇒♢α.Similarly,we can prove ♦α ⇔¬■¬α.

(4) Clearlyα ⇒¬¬α.By rule (□L) and (□R),one obtains □α ⇒□¬¬α.Then¬□¬¬α ⇒¬□α.By (3),♢¬α ⇒¬□α.Then¬¬□α ⇒¬♢¬α.Further since □α ⇒¬¬□α.Hence by (Cut),□α ⇒¬♢¬α.Conversely,by (¬¬),¬¬□¬α ⇒□¬α.Then by (3),¬♢α ⇒□¬α.Therefore,¬♢¬α ⇒□¬¬α.By(⋆¬¬),one obtains □¬¬α ⇒□α.Thus by(Cut),¬♢¬α ⇒□α.Similarly,we can prove ■α ⇔¬♦¬α. □

LetTbe a set of formulas.LetT⋆={♢α,♦α |♢α,♦α ∈T}and¬T⋆={¬α|α ∈T⋆}.Letc(T⋆∪¬T⋆)be the conjunction and disjunction closure ofT⋆∪¬T⋆,andb(T⋆)be the conjunction,disjunction and negation closure ofT⋆.Clearlyc(T⋆∪¬T⋆)⊆b(T⋆).Define¬¬c(T⋆∪¬T⋆)={¬¬α|α ∈c(T⋆∪¬T⋆)}.