基于瞬变冲激时刻的地-井TEM 快速定量解释方法

智庆全，武军杰，王兴春，杨 毅，张 杰，邓晓红

(1.中国地质科学院地球物理地球化学勘查研究所，河北 廊坊 065000；2.自然资源部地球物理电磁法探测技术重点实验室，河北 廊坊 065000；3.长安大学 地质工程与测绘学院，陕西 西安 710054)

地-井瞬变电磁法(Transient Electromagnetic Method，TEM)是一种将发射装置布设在井孔上方或附近平面上，在钻孔中逐点测量的电磁探测方法。相比于传统的地面瞬变电磁法，其接收系统置于钻孔中，大地的滤波作用能够有效压制高频干扰，提高观测数据的信噪比；接收装置更加靠近地质体，能够近距离获取异常响应，对薄层、井旁地质体等探测目标具有更强的分辨能力。多年来在固体矿产资源勘查[1-3]、煤田采空区探测[4-5]巷道超前预报[6-7]等方面得到了广泛的应用并取得了良好的勘查效果。

作为一种地下电磁探测方法，地-井瞬变电磁的响应特征和解释理论相比地面瞬变电磁法更为复杂。在地-井瞬变电磁响应的正演模拟方面，J.R.Wait 等[8-10]较早地开展了理论分析工作，推导了均匀半空间情况下地-井瞬变电磁响应的积分表达式和特殊情况下的解析表达式，奠定了响应特征分析的理论基础。之后，学者们采用数字滤波方法实现了地下电磁场的一维正演[11-13]，通过有限元[14-15]、有限差分[16-18]、有限体积[19]等方法实现了复杂模型的全空间电磁场三维模拟。目前，地-井瞬变电磁的响应模拟理论已较为成熟，关于其响应特征和规律的总结也渐趋完善。

在地-井瞬变电磁的数据解释方面，M.N.Nabighian[20]首先分析了瞬变电磁场在地下的扩散特征，指出地表电磁场可以通过地下的一个电流环进行等效，电流环在大地-空气界面的作用下向深部和外部扩散，即著名的“烟圈”理论，从物理上阐明了瞬变电磁场在地下的扩散规律，同时也提供了一种较为快捷的数据解释方法。但该理论的应用范围局限于地表以上的电磁场，对于地-井瞬变电磁数据并不适用。A.Ziolkowski[21]、罗维斌[22]、汤井田[23]等通过对海洋瞬变电磁法的模拟分析，发现不同偏移距的电场响应在时间上存在一个“峰值”，进而提出了瞬变冲激时刻[21-23]的概念，并指出冲激时刻与介质电阻率相关，通过冲激时刻可计算出介质电阻率值。部分学者总结提出了一套实用的地-井TEM 数据采集技术，以及从定性分析到半定量的解释技术，采用矢量交会技术实现了地-井TEM 井旁异常的快速定位[24]，采用电流环等效实现了纯异常近似三维反演[25]，并初步研究了地-井TEM 数据的视电阻率定义方法[26]。

综合以上研究可以发现，当前已有的地-井TEM解释方法中，基本上以定性分析和近似反演等半定量解释方法为主，以视电阻率定义、一维反演为代表的快速定量解释技术研究较少且尚不成熟，而解释效果最佳的三维反演技术时间成本过高，难以实现快速定量解释。最终导致地-井瞬变电磁测量成果往往仅能以响应曲线、交会矢量、电流环位置等形式呈现，不能直观地反映地下介质的电阻率分布。鉴于此，笔者基于前人关于瞬变冲激时刻的研究，提出一种地-井TEM 数据的快速定量解释方法，利用地下瞬变电磁场的冲激时刻定义大地视电阻率，通过研究瞬变电磁场扩散速度与深度的关系，导出地层真电阻率的求取方法。该方法理论基础可靠，计算速度快、对大地真实电阻率恢复程度高，具有较高的实用价值。

1 地-井瞬变电磁响应的冲激时刻

关于瞬变电磁烟圈效应和冲激时刻的已有研究结果表明，当发射源和接收点的位置存在偏移量时，电场分量在早期较小，随时间推移逐渐增大并达到峰值，然后开始衰减，晚期呈现单调的衰减特征，电场达到峰值的时刻称为瞬变冲激时刻。冲激时刻的早晚取决于瞬变电磁场在空间上的扩散速度，大地电阻率越高，电磁场扩散速度越快，冲激时刻越早。对于地-井瞬变电磁法而言，一般观测地下的磁场分量(dB/dt)，因此，首先需要对磁场响应的冲激时刻特征进行分析。

J.R.Wait 等[9]首先推导了均匀半空间的地-井瞬变电磁响应表达式。对于电导率为σ的均匀大地，半径为a的发射回线位于地表，其中供有大小为I0的电流，接收点P位于地下，如图1 建立柱坐标系，取向上为Z轴正方向。在t=0 时刻瞬间撤掉发射回线中的电流后，P点磁场响应表达式为：

图1 均匀半空间模型和地-井TEM 测量Fig.1 Diagram of the half-space model and surface-borehole TEM

式中：Br和Bz分别为磁场的径向和垂向分量；μ为大地磁导率；h为接收点深度；r为接收点与坐标原点的水平偏移距离；A为发射回线的相对半径，A=a/h；m(t)和q(t)分别为包含有第一类贝塞尔函数J0和J1的无穷积分；D=r/h；T=t/(σμh2)；Z=z0/h；z0为发射回线在地表以上的高度；f(x)=2J1(x)/x。式中的无穷积分可通过快速汉克尔变换法[27]求取。

为了直观地分析地-井瞬变电磁响应的特征和规律，分别计算了均匀半空间模型在不同深度接收点和不同电阻率、相同接收点2 种情况下的dBz/dt响应，结果如图2 所示。在图2a 中，均匀半空间电阻率ρ=100 Ω·m，发射回线位于地表z=0 m 位置，半径为100 m，发射电流1 A，接收点位于地下(-10 m,10 m,-h)位置，深度h的范围设置为0～600 m，间隔100 m。图2b 中，接收点深度固定为300 m，模型电阻率分别设置为10、30、100、300、1 000 Ω·m。由图2 可知，瞬变电磁场在地下传播时，dBz/dt响应在时间上存在一个峰值，其对应时刻即为dBz/dt响应的冲激时刻，且冲激时刻的早晚取决于大地电阻率和接收点深度：深度越大、大地电阻率越低，峰值时刻出现越晚。

图2 均匀半空间的地-井TEM 响应Fig.2 Surface-borehole TEM responses of uniform half-space

根据冲激时刻的定义，分别采用电阻率为10、100、1 000 Ω·m 的均匀半空间模型，绘制在不同井位、不同深度上dBz/dt响应的冲激时刻tp，如图3 所示，并进行多项式曲线拟合。其中设计井位Hole 1 的水平坐标为(-10 m,10 m)，Hole 2 的水平坐标为(80 m，50 m)。由图3 可知，冲激时刻随大地电阻率的增加而变早，二者之间存在反比例关系；冲激时刻随深度的增大而变晚，其增加速率高于线性函数。结合不同电阻率大地的冲激时刻曲线拟合结果，进行分析可以发现，冲激时刻随深度变化的函数呈现二次型特征，近似有函数关系：

图3 冲激时刻随深度变化的函数图Fig.3 Function diagram of impulse time varying with depth

式中：tp为冲激时刻，ms；ρ为大地电阻率，Ω·m；K为一个常量系数，ms·Ω·m-1，对于Hole1有K≈ 1.23×10-4ms·Ω·m-1，对于Hole2 有K≈ 1.30×10-4ms·Ω·m-1，二者之间的差距约为5.38%。

2 视电阻率定义和大地电阻率求取方法

关于准静态条件下电磁场扩散规律的研究表明，电磁场在均匀大地中的极大值位置是仅仅关于大地电导率和时间的函数，与发射回线几何形状、发射电流等无关[20]。进一步研究表明，地下瞬变电磁响应的dBz/dt分量的极大值深度[28]可以近似表示为：

式中：b为一个常数，在1 阶至3 阶级数近似条件下，分别有b(1)=8，b(2)=12，b(3)≈ 9.112。简单整理可以发现，该式的计算结果与式(3)十分接近，表明二次函数完全可以作为冲激时刻随深度变化函数的一个较好的近似。

在已知接收点深度h和冲激时刻tp的情况下，根据式(4)即可求得大地电阻率值，即有基于瞬变冲激时刻的视电阻率定义：

根据此式即可直接计算不同深度接收点的视电阻率。考虑到级数近似所固有的误差，本文在实际计算时直接采用式(2)，基于反函数理论[29]，通过迭代来获取更为精确的视电阻率值。

以上视电阻率定义方法直接基于瞬变电磁场在大地中的冲激时刻，主要反映接收点所在深度以浅大地介质的总体电性特征，具有较强的“体积效应”。为更加精细地恢复大地电阻率的分布，本文基于电磁场扩散速度，给出一种改进的大地电阻率计算方法。假设大地由多个电阻率均匀的薄层组成，根据式(4)有均匀介质中瞬变电磁场的扩散速度：

对于第i个薄层，其顶、底界面深度分别为hi和hi+1，冲激时刻分别为ti和ti+1，对应的视电阻率分别为和，则有：

又根据速度的物理定义有：

联立式(6)和式(8)，将式(7)代入并整理可得第i薄层的电阻率：

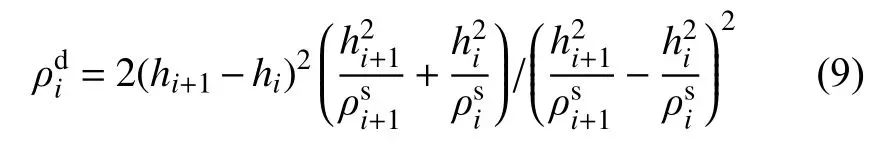
式(9)即为各层大地电阻率的计算公式，该式不包含系数项b，与渐近级数的阶数无关。这种电阻率计算方法实际上基于瞬变电磁场在大地中的扩散速度，相比基于冲激时刻的视电阻率而言，通过式(9)计算得到的电阻率受体积效应影响更小，更接近真实大地电阻率。由于无需进行复杂模型的响应拟合计算，该算法具有计算简单、时间成本低、无多解性的特点，适用于地-井TEM 数据的快速定量解释。

3 模型算例

为检验上述基于冲激时刻的地-井TEM 数据快速解释方法的正确性和有效性，选择了一维模型系列进行数值模拟计算。一维模型主要选择D、G、H、K型4 种典型地电断面，各层的电阻率ρ和厚度H见表1。观测参数参照实际工作中常用的工作装置进行设置，发射回线位于地表z=0 m 位置，回线边长为100 m，发射电流1 A，井孔位于(-10 m,10 m)位置，钻孔为直孔，接收点深度范围为0～600 m，间隔10 m。

表1 一维层状模型参数Table 1 Parameters of 1D models

图4a 为均匀半空间情况下基于冲激时刻定义的视电阻率ρs和基于扩散速度恢复的大地电阻率值ρd。由图4a 可知，在不同深度的接收点上，基于冲激时刻定义的视电阻率和基于扩散速度恢复的大地电阻率基本一致，且与设计模型吻合较好，证明了所提出算法的正确性。图4b 为计算电阻率数据与设计模型的相对误差，ρs和ρd与设计半空间电阻率的最大相对误差分别为0.28%和2.06%。这是由于式(9)中包含了对大地电导率的差分计算，使得ρd在数值稳定性上弱于基于冲激时刻的视电阻率ρs，导致其相对误差较大。

图4 均匀半空间计算电阻率随深度的变化Fig.4 Variation of calculated resistivity with depth in uniform half-space

图5 为两层D 型模型和G 型模型的ρs和ρd计算结果，并与设计模型电阻率(ρtrue)进行了对比。由图5 可知，ρs和ρd均能较好地反映出两层模型的电阻率变化趋势，但ρs曲线较为宽缓，ρd曲线变化较为迅速且存在振荡现象。随深度增大，ρd总能更早地体现出大地的电阻率变化，且与真实大地电阻率更为接近。这表明，虽然ρd的数值稳定性较弱，但其对大地电阻率变化的灵敏度高于ρs，对大地的电性界面位置反映也更为精细。

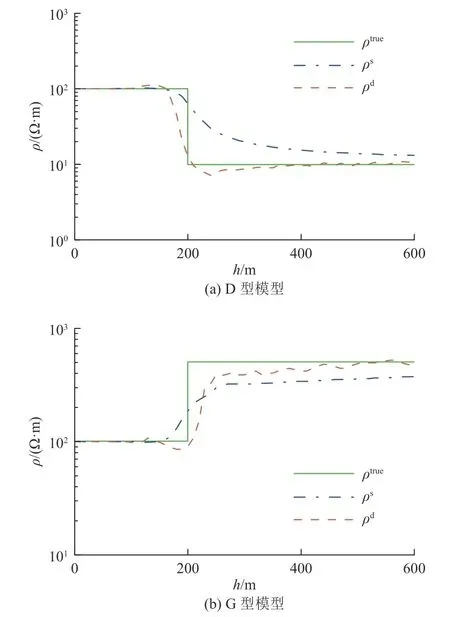
图5 两层模型计算电阻率随深度的变化Fig.5 Variation of calculated resistivity with depth in 2-layer models

注意的一点是，虽然ρd对大地电阻率变化更为灵敏，但其电阻率曲线存在与传统视电阻率定义类似的“overshoot”和“undershoot”现象，即在低阻地层中会伴随产生一个略弱的“假”高阻层，反之在高阻地层中也同样会伴随产生一个略弱的“假”低阻层。在进行资料解释工作时，需对这种现象加以考虑，避免造成与真实电阻率变化特征相反的错误解释。

图6 为三层H 型模型和K 型模型的ρs和ρd及与设计模型的对比结果。由图6 可知，ρs和ρd对低阻薄层反映较好，ρs完整体现出了大地电阻率高-低-高的变化趋势，ρd基本上准确地恢复了薄层和背景大地的电阻率值。对比薄层顶、底界面的恢复电阻率结果可以发现，ρd对顶界面反映较为清晰，而底界面较为模糊，低阻范围延续较长。这是由于随深度增加，瞬变电磁场对地层的分辨能力迅速降低。ρs和ρd对高阻薄层反映效果均欠佳，仅能体现出高阻薄层的存在和大致位置，未能准确恢复薄层电阻率值。在一定程度上而言，这是由瞬变电磁法对于高阻层的不灵敏特性所造成的。高阻层的存在本身对于瞬变电磁场分布和传播特征的影响，相对低阻层而言较弱。

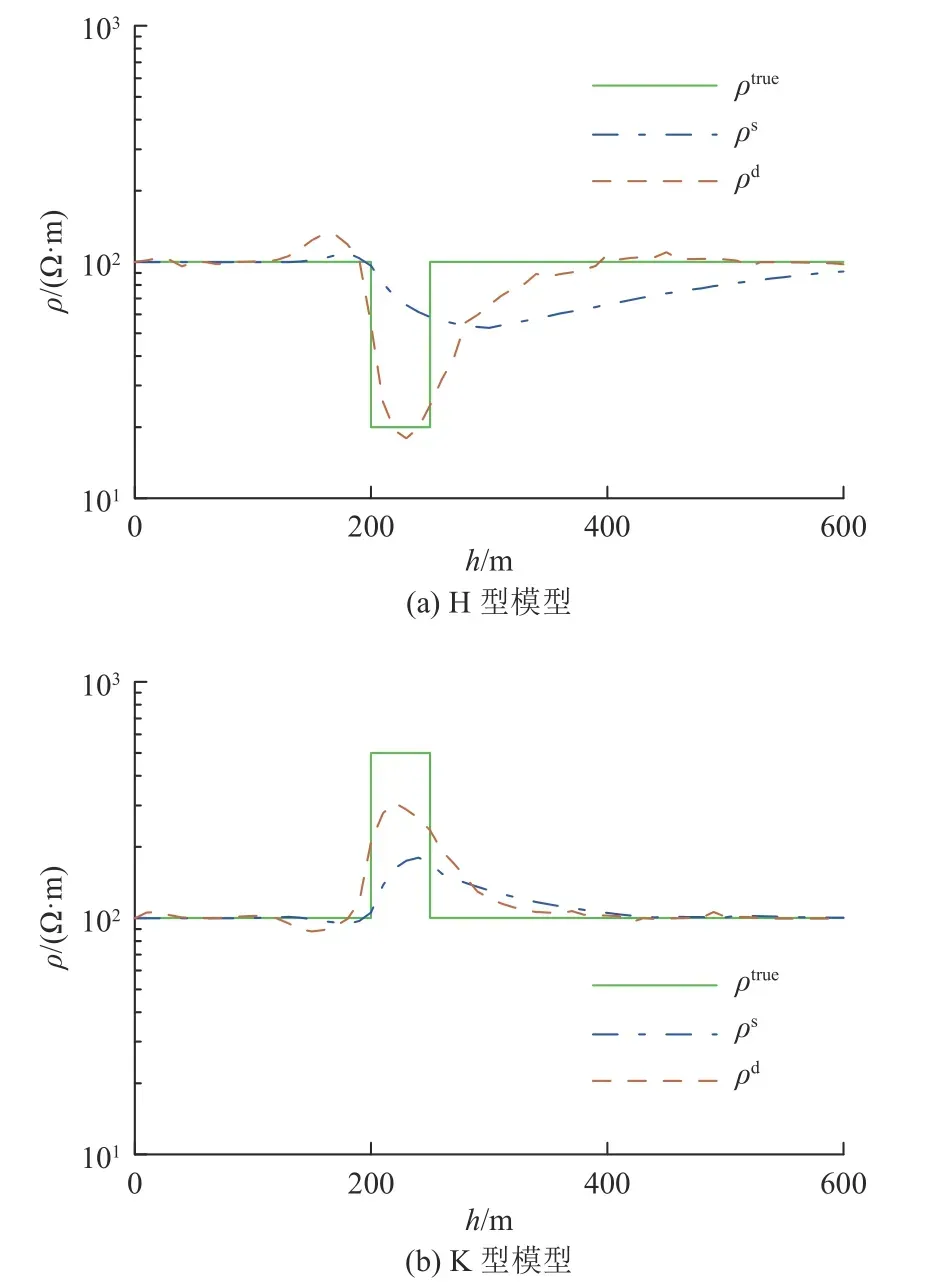
图6 三层模型计算电阻率随深度的变化Fig.6 Variation of calculated resistivity with depth in 3-layer models

4 体积效应探讨

瞬变电磁法作为一种基于扩散场理论的感应类电磁勘探方法，本身固有体积效应。式(9)基于电磁场的垂向扩散速度给出了大地电阻率的改进计算方法，在一定程度上削弱了垂向体积效应的影响，所获得的大地电阻率可以近似看作井孔中相邻接收点间介质的综合效应，但其对应不同深度的径向体积效应仍需进一步探讨。

在均匀半空间条件下，瞬变电磁感生涡流的极大值同时向下和向外传播[20,28]，其包络面为一个与地面夹角约为25°的锥形斜面。据此可导出包络面半径(R)与深度的关系：

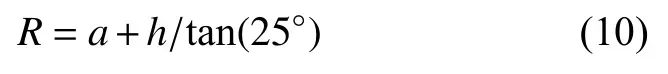
式中：a为发射回线半径。

根据涡流电场所产生的磁场分布规律，在该半径范围内，瞬变电磁磁场响应较为均匀且具有较大的强度，并在超出该半径范围后快速衰减，此时可将井孔中接收点接收到的瞬变电磁信号看作主要是涡流半径范围内介质的综合效应。由式(10)可以发现，通过前文算法所得出大地电阻率的体积效应取决于发射回线的半径和接收点深度：发射回线半径越大、接收点深度越深，体积效应越强。

5 实测数据试算

为进一步检验本文算法的有效性和实用性，选取了某矿区的地-井TEM 实测数据进行了试算。所测量钻孔的终孔深度为2 000 m，受钻孔套管和井况限制，地-井TEM 实测深度范围为950～1 700 m，该井段同步开展了0.5 m 普通电阻率测井工作。地-井TEM 工作采用的观测参数为：方形发射回线，边长300 m，发射电流20 A，发射基频12.5 Hz，观测时窗0.052～15.96 ms，接收点垂直间隔5 m。

图7a 为不同深度上的dBz/dt响应曲线。由图7a可知，随深度增大，dBz/dt响应曲线的峰值时刻逐渐后移。图7b 为根据dBz/dt响应曲线拾取的冲激时刻曲线，可以发现冲激时刻总体随深度增加而变晚。但受拾取误差、噪声和测量误差等因素的影响，冲激时刻曲线存在振荡。冲激时刻曲线的变化率反映了电磁场的扩散速度特征，整体呈现“慢-快-慢”趋势，表明地下介质电阻率呈“低-高-低”趋势变化。采用本文算法分别计算了ρs和ρd，并与电阻率测井结果(ρl)进行了对比，如图7c 所示。由图7c 可知：ρs较好地反映出了大地电阻率“低-高-低”的变化趋势，与电阻率测井结果的总体趋势一致；ρd更加灵敏地反映出了大地电阻率值的变化，且与电阻率测井结果基本吻合，特别是对于1 500 m 左右深度的低阻界面位置反映较为精准。该实测数据算例表明，基于瞬变冲激时刻的视电阻率定义算法能够较好地反映出大地电阻率的整体变化趋势，基于瞬变电磁场扩散速度的改进算法能较为准确地恢复大地电阻率值，对电性界面反映较好，具有较强的实用性。

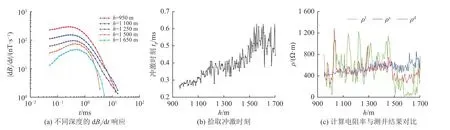
图7 实测数据计算结果Fig.7 Calculated results of the field data

6 结论

a.借鉴关于TEM“烟圈”效应和冲激时刻的已有研究成果，探讨了地-井瞬变电磁响应的冲激时刻特征，给出了dBz/dt冲激时刻与大地电导率和深度之间的函数关系。在此基础上，提出了一种基于瞬变冲激时刻的地-井TEM 视电阻率定义方法，并改进大地电阻率的精确恢复算法。模型计算和实测数据试算结果表明，基于冲激时刻的视电阻率定义算法能够较好地反映设计模型的电性变化趋势，基于扩散速度的大地电阻率计算方法能够更为精确地恢复出大地电阻率值和电性界面，可用于地-井TEM 数据的初步定量解释。

b.基于瞬变冲激时刻的地-井TEM 定量解释方法相比传统的定性和半定量解释方法，具有直接获取大地电阻率参数的优势。相比反演解释方法，不需要进行复杂模型的正演迭代，具有较高的计算效率。

c.模型计算结果表明，基于冲激时刻的视电阻率定义方法仍然存在“overshoot”和“undershoot”现象，在实际资料处理中，应加以考虑，避免造成错误解释。

d.鉴于瞬变电磁电场E和磁场B的优良特性，利用E场和B场冲激时刻的视电阻率定义方法或能避免“overshoot”和“undershoot”现象，具备进一步研究的价值。

e.基于瞬变冲激时刻的地-井TEM 定量解释方法属于一种快速、初步的定量方法，仅利用了地-井TEM 数据的冲激时刻特征，其余大量的有效信息并未参与计算。而地-井TEM 方法深入地下展开测量，既包含有随深度增加的“几何测深”信息，又包含有随时间增加的“时间测深”信息，获取的地电信息十分丰富。先利用冲激时刻、视电阻率定义等方法提供初始地电模型，再利用高维反演或近似高维反演获取钻孔周边和深部的高分辨电性分布信息，是地-井瞬变电磁法数据处理解释的一条可取途径。