改进二次型Buck-Boost变换器的研究与分析
朱高中,刘树林,王 成 ,李雪婷
(1.西安科技大学 电气与控制工程学院,陕西 西安 710054;2.渭南师范学院 物理与电气工程学院,陕西 渭南 714099)
环境污染和气候变化对地球的危害越来越明显,利用新型可再生能源替代化石材料来生产能源成为近年来研究的一个热点,目前具有升压/降压能力的DC-DC变换器已经广泛应用于煤矿、石化、电力、太阳能光伏发电、燃料电池等可再生能源诸多领域[1-11],其中太阳能光伏发电、燃料电池等新能源发电方式输出直流电压为18~50 V,不能满足后级逆变并网要求,故此系统前端的直流变换器输出电压必须提高到200~600 V甚至更高电压时才能满足不同场合的需求,因此要求变换器具有较高的电压增益,同时要求变换器具有连续的输入输出电流。传统的Buck-Boost变换器虽然结构简单,但其输入、输出电流不连续,同时其电压增益也受到限制。文献[12-14]采用电压举升技术来提高变换器的电压增益,但采用该方法造成电路结构和体积成本的增加。文献[15-18]采用交错技术来提高变换器的电压增益范围,但其拓扑工作模式和控制方式比较复杂。
针对上述文献的不足,本文研究二次型变换器。目前已有许多文献提出二次型Buck-Boost变换器。Maksimovic等[19]提出较早的二次型Buck-Boost变换器,但由于二极管钳制使得其只能工作于降压模式。文献[20-24]所提二次型Buck-Boost变换器的负载电流是不连续的,会导致输出纹波增大。Sarikhani等[25]提出的二次型Buck-Boost变换器具有连续输入电流和正输出电压,但其输出电压增益不够理想。文献[20-25]变换器的电压增益比均为D2/(1-D)2。
针对上述二次型Buck-Boost变换器的缺点,本文通过在文献[25]二次型Buck-Boost变换器的后级级联开关电容单元和LC低通滤波器,提出一种改进的新型二次Buck-Boost变换器。与文献[25]变换器相比,该变换器不仅具有较高二次电压增益,且在相同输出电压情况下,降低了输出纹波电压和开关器件的电压应力。
1 改进的新型二次Buck-Boost变换器工作原理分析
文献[25]二次型Buck-Boost变换器原理如图1所示,该二次型Buck-Boost变换器的电压增益比为

图1 改进前的二次型Buck-Boost变换器
(1)
改进二次型Buck-Boost变换器原理如图2(a)所示,与文献[25]二次型Buck-Boost变换器相比,改进二次型Buck-Boost变换器中开关电容单元代替了文献[25]变换器中二极管D2,开关电容单元由电容CN、CP和二极管D2、D3组成且满足电容CN=CP;而LC低通滤波器由是电感L3和电容C0组成。为了更好地分析电路的工作原理,假设变换器中所有器件均不考虑寄生参数的影响;变换器中所有电感均工作在连续导电模式。
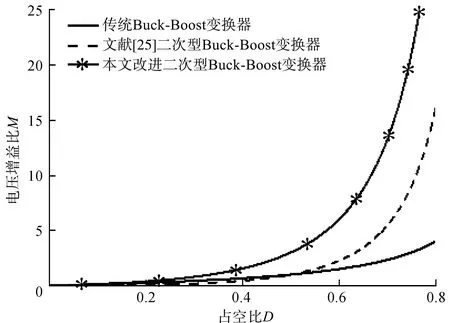
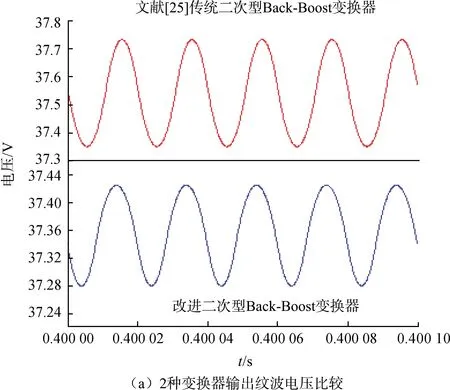
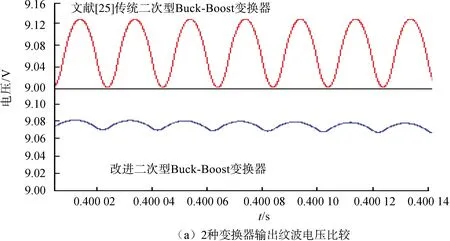
状态1:开关管S1、S2同时开通,其等效电路如图2(b)所示。此状态下,D1、D2、D3呈反偏状态而截止。输入电源Vi和电容C1储存能量分别对电感L1、L2供电,电感L1、L2的电流线性上升。电容CN、CP储存的能量共同给电感L3和负载供电,从工作原理可知,流过开关管S2的电流为iL3-iL1,当电流iL3>iL1时,电流从开关管S2流出,否则电流iL3 (2) 状态2:开关管S1、S2同时关断,其等效电路如图2(c)所示。此状态下,D1、D2、D3呈正偏状态导通,输入电压Vi和电感L1储存能量经二极管D1给电容C1供电,电感L2、L3反向串联将储存能量给并联电容CN、CP和负载供电,由于电容CN和CP并联充电,因此可知VCN=VCP=VC,根据此状态的工作原理可得: 图2 改进二次型Buck-Boost变换器的原理及等效电路 (3) 对电感L1~L3应用伏秒平衡原理,由式(2)和式(3)可得: (4) 式(4)中D表示开关管的占空比。由式(4)可得改进二次型Buck-Boost变换器的电压增益比为 (5) 通过式(5)可以看出,改进二次型Buck-Boost变换器的电压增益比是文献[25]二次型Buck-Boost变换器电压增益比的(1+D)/D倍。图3给出了3种变换器电压增益比的比较,由图3可知,在同等占空比下本文所提变换器具有更高的电压增益比。 图3 3种变换器电压增益比的比较 设电感L1~L3的纹波电流用ΔiL1~ΔiL3表示,由式(2)得电感L1~L3的纹波电流表达式为: (6) 根据安秒平衡原理,由式(2)和式(3)可得电感L1、L2、L3的平均电流为: (7) 设流过电感L1~L3的谷值电流分别为IL1V~IL3V,由式(6)和式(7)可以求出电感L1~L3的谷值电流分别为: (8) 式(8)中I0表示输出端的平均电流。为确保所有电感工作在连续导电模式状态(CCM),由式(8)可得电感L1~L3的电感值必须满足条件: (9) 1.2.1 开关管和二极管的电压应力分析 设开关管S1、S2电压应力为VS1、VS2,由工作原理可得其电压应力为: (10) 同理可得二极管D1~D3承受电压应力为二极管截止时所承受的电压应力,二极管D1~D3电压应力VD1~VD3为: (11) 1.2.2 开关管和二极管电流应力分析 由状态1可得开关管S1、S2电流应力IS1、IS2为: (12) (13) 电容参数取值影响电容输出纹波的大小,电容纹波电压大小将会影响变换器的稳定性。在纹波电压给定的范围,可以通过计算输出纹波电压来确定电容值的大小。设电容C1、CN、CP、C0输出的纹波电压分别为ΔVC1、ΔVCN、ΔVCP、ΔVC0,由改进二次型Buck-Boost变换器工作原理及式(2)分析可知,电容C1、CN、CP、C0输出的纹波电压为: (14) 表1对本文改进的二次Buck-Boost变换器及其他变换器从电压增益比、开关器件电压应力、输入输出电流类型等方面进行比较。从表1对比结果可以看出,本文变换器和文献[19]变换器相比,电压增益明显增大,开关器件的电压应力减小。同时文献[19]变换器只能工作在降压模式。与文献[20]变换器相比,本文变换器虽然多了一个电感、2个电容和一个二极管,但改进的变换器不仅输出电压增益大于文献[20]变换器,而且在同等电压值情况下减小了开关管的电压应力,具有连续输入和输出电流。同时输出端带有滤波电路,减小了输出电压纹波,满足了实际应用中的电磁干扰/兼容问题。与文献[25]变换器相比本文改进的变换器多了1个电容和1个二极管,但是电压增益明显高于文献[25]变换器,且改进的变换器中开关管和二极管的电压应力大大减小。通过对比可见,改进二次Buck-Boost变换器具有优良的性能。 表1 本文变换器与其他变换器之间的比较 为了分析本文改进二次型Buck-Boost变换器小信号动力学特征,需要建立变换器小信号数学模型。利用状态空间平均法建立小信号模型方程,在考虑到工作原理基础上,根据前文的分析并考虑到VCN=VCP=VC前提下,由式(2)和式(3)可得: (15) 式中:〈iL1〉、〈iL2〉、〈iL3〉、〈vC1〉、〈vC〉、〈vo〉、分别表示iL1、iL2、iL3、vC1、vC、vo平均分量;d表示小信号模型下的占空比。 对每一个参数的平均变量进行分解时,可以分解为直流分量和交流小信号分量之和,对平均变量〈iL1〉、〈iL2〉、〈iL3〉、〈vC1〉、〈vC〉、〈vo〉分解为: (16) 将式(16)代入式(15),在忽略交流二阶项情况下,可得出改进二次型Buck-Boost变换器小信号模型为: (17) 通过对式(17)进行拉普拉斯变换,可以计算出控制-输出传递函数,这在控制器设计中起重要的作用。 为了验证改进二次型Buck-Boost变换器性能,给定变换器的电路参数如表2所示。利用PSIM软件建立2种变换器电路的仿真系统模型。 表2 仿真实验参数 在占空比均为0.4时,2种变换器输出电压波形如图4所示,由图4可得在占空比相同情况下,本文改进变换器的输出电压明显高于文献[25]变换器的输出电压。 图4 2种变换器输出电压比较(D=0.4) 为了进一步验证改进二次型Buck-Boost变换器相比文献[25]变换器能够降低输出电压纹波和减小开关器件的电压应力,在表2给定参数情况下,当2种变换器工作在升压模式且输出电压值均为37.4 V时,改进变换器和文献[25]变换器所对应占空比分别为0.4、0.556。由图5(a)中2种变换器的输出纹波电压结果可知,在平均输出电压均为37.4 V情况下,改进变换器的输出电压纹波小于文献[25]变换器的输出电压纹波。由图5(b)波形可以看出改进二次型Buck-Boost变换器中开关管S1、S2电压应力值分别为66.8、26.7 V,而文献[25]变换器中开关管S1、S2电压应力值分别为121.7、67.5 V。同时改进二次型Buck-Boost变换器中开关管S1、S2电压应力值与式(10)理论结果一致。由图5(c)的波形可以看出改进二次型Buck-Boost变换器中二极管D1、D2电压应力值分别为40、26.7 V。文献[25]二次型Buck-Boost变换器中二极管D1、D2电压应力值分别为54、67.6 V。改进二次型Buck-Boost变换器中二极管电压应力值与式(11)理论结果一致。由2种变换器中开关器件电压应力对比可知,在平均输出电压均为37.4 V情况下改进二次型Buck-Boost变换器相对于文献[25]变换器的电压应力明显降低。 图5 2种变换器在升压模式下波形比较 当2种变换器工作在降压模式且输出电压均为9 V时,改进变换器和文献[25]变换器所对应的占空比分别为0.20、0.379。由图6(a)输出电压纹波的对比可得改进变换器电压纹波小于文献[25]变换器电压纹波。由图6(b)波形可以看出改进变换器中开关管S1、S2电压应力值分别为37.4、7.5 V,而文献[25]二次型Buck-Boost变换器中开关管S1、S2电压应力值分别为62.5、23.8 V。由图6(c)波形可得改进二次型Buck-Boost变换器中二极管D1、D2电压应力值分别为29.9、7.5 V。文献[25]二次型Buck-Boost变换器中二极管D1、D2电压应力值分别为38.7、23.8 V。通过2种变换器开关器件的电压应力对比可知,在输出平均电压均为9 V情况下,改进二次型Buck-Boost变换器的开关器件电压应力小于文献[25]二次型Buck-Boost变换器的开关器件电压应力。 图6 2种变换器降压模式下波形比较 将文献[25]二次型Buck-Boost变换器和开关电容单元、LC低通滤波器相结合,本文提出一种改进二次型Buck-Boost变换器,分析了该变换器的工作原理、开关器件的电压电流应力和输出纹波电压,并利用PSIM仿真软件在升压和降压模式下对改进二次型Buck-Boost变换器进行了仿真验证,理论分析和仿真实验结果均表明改进二次型Buck-Boost变换器具有以下优点: 1)改进二次型Buck-Boost变换器具有较高的电压增益; 2)变换器输出端连接有低通滤波器,降低了输出电压纹波; 3)在输出电压值相等的情况下,改进二次型Buck-Boost变换器中开关器件的电压应力较小。
1.1 电感电流及纹波分析
1.2 开关管和二极管的电压电流应力分析
1.3 电容纹波电压分析
2 不同拓扑结构比较

3 小信号建模分析

4 实验分析


5 结论

