基于任务的维修保障设备携行配置研究
李黄琪,蔡开龙*,郝 明,薛红阳,濮志刚,陈 勇
(1.南昌航空大学 飞行器工程学院,江西 南昌 330063;2.空军工程大学 航空机务士官学校,河南 信阳 464000)
维修保障设备是飞机保障资源的重要组成部分,建立科学的飞机保障设备配备标准,合理配置维修保障设备是确保飞机保障任务顺利完成的前提和基础。基于不同的飞机作战任务,需要携带的维修保障设备会有差异,如果维修保障设备配置过少,将导致保障工作出现“人等设备”的情况,直接影响飞机保障工作的进度;如果维修保障设备过多,虽然能够保证维修工作的顺利开展,但是会增加飞机的负载,进而影响飞行任务的执行效率,甚至可能出现不必要的安全隐患。所以科学合理的航空维修保障设备配置方案,可提高维修保障设备的利用率,大幅缩减航空维修保障任务的等待时间,同时还能保障飞机战备完好率,进而缓解现阶段航空维修保障能力不高的现状。
目前分析维修保障设备的研究有:根据分析维修任务的分配和保障资源的需求,定性地确定备件需求品种[1];运用Petri 网理论[2]构建模型,获得所需的维修保障装备;运用排队论理论对维修保障装备数量进行计算;应用多约束条件下维修保障设备配置方法。以上方法都没有定性定量相结合的分析,一部分方法只是主观地给出了需要携带的维修保障设备品种,另一部分方法是客观的理论研究并没结合具体的飞行任务分析。因此本文通过定性定量相结合的方法分析3 种飞行任务确定出3 种维修保障设备的类型,并根据飞机维修过程建立排队系统。最终建立评估模型对满足要求的方案进行评估,选出最优维修保障设备携行方案[3-9]。
1 维修保障设备携行配置方法的整体思路
维修保障设备携行优化方法整体思路模型,如图1 所示。首先本文根据飞行任务之间的差异,将飞行任务类型分为:基本飞行、任务一飞行和任务二飞行;其次确定出在不同的飞行任务下所需要携带的维修保障设备品种的分类,并与相关的飞行任务类型相对应。而维修保障设备品种的数量确定,可以根据飞机维修的过程建立排队系统,通过机群数量、飞机装备的故障率和维修设备的修复率计算出需要维修保障设备的数量。由于飞机飞行所要求的维修保障设备数量是越多越好,但是所能携带的空间有限。所以需要在评估优化中选用战备完好率、等待维修时间和携行空间3 个评估优化指标用熵权法-TOPSIS[10]法对给出的所有维修保障设备携行方案进行评估,最后筛选出最优维修保障设备携行方案。
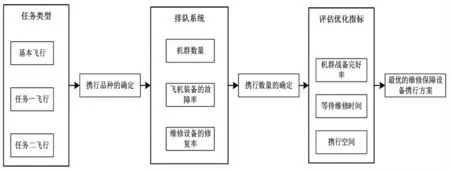
图1 维修保障设备携行优化方法思路模型
2 建模分析
2.1 维修保障设备携行品种的确定
航空维修保障按照作战、训练任务不同,有不同的保障任务。基于任务类型的不同,我们可以把飞行任务分为:基本飞行,任务一飞行和任务二飞行。基本飞行是指只需满足日常飞行训练任务,其维修内容为日常维护;任务一飞行是指需要执行任务一的飞行,其维修内容有日常维护还有任务一需求的维修保障;任务二飞行是指在飞行期间飞机需要进行任务二的飞行工作,其维修内容有日常维护和任务二飞行所需要的维修保障。根据飞机要执行的任务类型可以将需要携带的维修保障设备分为3 个类型:(1)基本飞行包,主要是按照典型出动规模,保障飞机基本飞行必要的保障设备;(2)任务一飞行包,主要是飞机在执行任务一飞行中所需要的维修保障设备;(3)任务二飞行包,主要是按照典型出动规模,完成飞机任务二飞行所需要的保障设备。见表1。其中的关键维修设备定义为完成某项维修保障任务,使得任务可行而必不可少的维修设备。换句话说,缺少了该维修设备,该维修保障任务就不可能完成。不同的飞行任务,对于关键维修设备的要求是不同的,比如需要挂弹飞行时,武器系统检测设备必须要充足可用,能够在规定时间内满足挂弹准备和检查工作,武器系统检测设备就是关键维修设备;执行日常飞行训练任务或不挂弹飞行任务时,武器系统检测设备就可以不必携带,因为缺少它不影响保障任务的完成,因此,该设备可看作该典型任务下的非关键维修设备。

表1 任务类型及用到的关键维修设备
2.2 维修保障设备携行数量的确定
飞机维修保障的过程在维修保障设备和工具充足的情况下,无须等待直接开展维修工作,维修完成以后,维修保障设备和工具等到下一个修理任务需要时使用;在维修设备和工具不满足需求的情况下,待修飞机进入维修队列等待,所以整个过程可以看作多顾客多服务台的排队系统。在一定的时间内若飞机停机维修的数量过多,则可能出现排队现象,导致机群的战备完好率因维修设备数量过少而降低。因此,维修设备的数量与机群的战备完好率直接相关。
根据排队论理论,该问题可看作是顾客源为有限的模型(M/M/c/∞/m)。假设y 表示飞机数量,c 表示维修设备套数。因此,y 为飞机数量(即M/M/c/∞/m 模型中的m),c 为维修设备套数(即M/M/c/∞/m 模型中的c)。M/M/c/∞/m 系统指飞机按照泊松流进入维修,维修时间间隔符合负指数分布,有c 个维修设备的并列维修系统。在该系统中,需要维修的飞机到达维修点后排成相应的队列,接受与维修专业特点相适应的维修设备的修理,每个维修设备的维修时间完全服从μ 的负指数分布,维修完毕后飞机按要求离开。该系统中,飞机的总量为y,并且存在y>c,飞机装备的故障率是常数λ,每个维修设备存在总体相同的修复率μ,同时,各维修设备的任务是独立的。
本文假设所有类型的维修保障设备在进行维修工作时都满足以下4 个条件。
(1)在某段时间间隔内,出现飞机维修任务的概率与这一时段的起始时刻无关,只与这时段的长短有关。
(2)飞机维修任务的数量与不同时间间隔无关,是相互独立的,即满足无后效性。
(3)假设在足够小的时间内,不能同时出现2 个以上的飞机维修任务(这种情况现实中基本成立),即,p(t)为同时出现2 个以上飞机维修任务的概率。
(4)在任意一段时间内有产出y 项飞机维修任务的概率为1,即满足有限性:。
如果飞机维修任务满足以上分析的4 个条件,依据巴尔姆-欣极限定理[8]断言:若能保证每个相互独立的小强度流是平稳有序的,则足够多的这些小强度流之和近似满足Passion 输入。因此我们可以认为,在t时间内有y 项需要进行维修的任务的概率服从强度为λ 的泊松分布

则在有y 架飞机需要执行维修任务时,该保障设备平均利用率(服务强度)为,式中λ 为飞机装备的故障率。c 为保障设备数量,μ 为设备平均修复率,有了设备的平均利用率,就可以利用M/M/c/∞/m 模型确定执行某一任务期间的保障设备数量。
根据排队论M/M/c/∞/m 模型理论分析,可求得状态
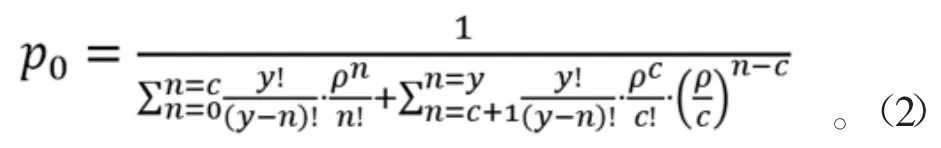
n 为受损飞机装备数量,如果0≤n≤c,则

如果c<n≤y,则

系统运行指标求得如下:

式中:Lq为等待修理的平均飞机装备数量,L 为系统中需维修的平均飞机装备数量(正在接受维修的飞机装备数量与正在等待维修的飞机装备数量之和)。
3 维修保障设备携行方案评估分析
维修保障设备优化评估指标体系是为了维修保障设备优化评估问题用较科学的数学方法进行量化处理,必须针对评估方案和评估目标建立一个科学的评估指标体系。维修保障设备的评估优化指标主要有3个,机群战备完好率δ、机群等待维修时间Wq和携行空间V。机群战备完好率是指装备系统的战备完好性在预定的平时与战时的利用率下承担和保持执行规定任务的能力,在多种维修任务并行的情况下本文将维修任务最低的战备完好率定为机群的完好率。机群等待维修时间这一指标是为避免排队的队伍过长造成拥堵,不利于维修保障工作的开展,在多种维修任务并行的情况下本文将维修任务最长的等待维修时间定为机群的等待维修时间。携行空间是指在携行运输中可以存放维修保障设备的空间(体积)有限的,携行空间可以看作是约束我们携带维修保障设备数量的指标。通过熵权法可以确定3 个评估优化参数的权重,再用TOPSIS 法对所有满足条件的维修保障设备携行方案进行排序,选出最优的维修保障设备携行方案。
熵权法-TOPSIS 法评估模型:设有m 个方案,n 个指标,Xij为第i 个样本第j 项指标的数值。因为方案指标的要求不同,可用极值标准化方法将指标分为极小值型指标与极大值型指标。其中,极小值指标是指标数据越小理想要求越好的指标:

极大值指标是指标数据越大理想要求越好的指标:
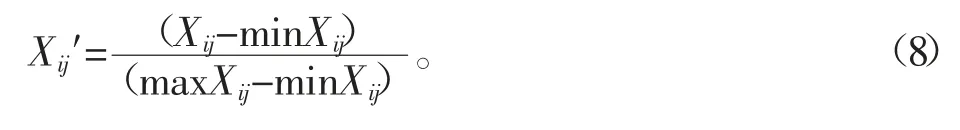
归一法,为了消除标准化后的指标值对数计算的影响,使得所有方案的指标都落在[0,1]之间,计算公式为:

计算第i 个方案第j 项指标占所有样本第j 项指标之和的比重Pij,公式为:

计算所有指标的熵值Ej,公式为:

计算所有指标的权重Wj,公式为:

对所有方案数据进行加权处理,公式为:

计算的所有方案数据的最好解Y+和最差解Y-,公式为:
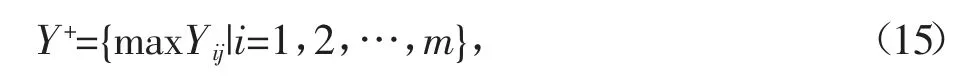
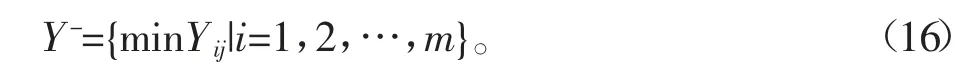
分别计算方案数据与最好解和最差解的距离Di+和Di-,公式为:

计算方案数据与最优解的接近程度Ci,所有综合得分公式为:

4 案例分析
假设典型任务下,需要出动某飞机机群,共有12架飞机。执行该任务需要用维修保障设备A、B、C 和D 4 种,维修保障设备A、B、C 和D 的信息,见表2。在携行空间1 200 cm3内,要保证每架飞机等待维修时间不能超过3 h,并且飞机机群战备完好率85%以上,最优应该携带多少设备?

表2 维修保障设备信息
通过分析我们可以知道A、B、C 和D 设备单个占用空间分别为:140 cm3、170 cm3、116 cm3和77 cm3;用排队论计算后,维修保障设备数量指标表见表3,从表中可以得出A、B、C 和D 4 个维修保障设备至少要携带2 个以上才能满足任务需求。

表3 维修保障设备数量指标表
因为机群的战备完好率是取所有设备完好率最低的,机群的维修等待时间也是取所有设备维修等待时间最长的。随着有某些设备维修保障数量的增加,机群的维修等待时间和战备完好率并没有发生改变。从表4 中的七个方案我们可以得出,方案一到方案四随着维修保障设备的增加并没有降低机群等待维修时间,也没有提高机群战备完好率,所以方案一到方案四中我们优先维修设备数量少的方案一,再由熵权法-TOPSIS法对方案一、方案五、方案六和方案七进行打分排序。

表4 方案评估参数表
通过熵权法求得战备完好率、等待维修时间、携行空间3 个评估指标的权重分别为:w1=0.2765,w2=0.2957,w3=0.4278;再将w1,w2,w3带入TOPSIS 法中得出所有方案的得分:方案一为0.4893、方案五为0.2037、方案六为0.2140、方案七为0.0929;由此可以看出方案一>方案六>方案五>方案七,所以我们的最优方案是方案一,需要携带维修保障设备A、B、C 和D 各2 个。
5 结论
本文采用定性定量相结合的方法进行系统的分析,首先对飞行任务进行分析,确定出3 种维修保障设备的分类,进而可以根据飞行任务确定出需要携带的维修保障设备的品种;其次运用了排队论方法和熵权法-TOPSIS 法,对携带不同的维修保障设备数量进行分析,并给出最优的维修保障设备携行方案。该方法的研究能够为确定飞行部队维修体系的研究提供参考,具备一定的应用价值,但在多军兵种联合作战的大趋势下如何确定适用于其他军兵种力量的维修保障体系仍是有待攻克的难题,因此未来在其他军兵种力量的维修保障体系需要进一步研究。

