异常高压对砂砾岩弹性性质影响的实验机理研究与压力预测新模型——以准噶尔盆地玛湖凹陷北斜坡三叠系为例

王斌， 赵建国*， 李伟， 黄玉， 尹路， 许多年

1 中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249 2 中国电建集团北京勘测设计研究院有限公司， 北京 100024 3 中国石油勘探开发研究院西北分院， 兰州 730020

0 引言

准噶尔盆地是我国西北地区一个勘探历史悠久的含油气盆地，砂砾岩储层在盆地西北缘的玛湖凹陷广泛发育(陈发景等，2005；李鹭光等，2020).近年来，在玛湖凹陷斜坡-凹陷区多套地层的砂砾岩储层中连续获得勘探突破.已钻井资料证实，这些砂砾岩储层以水下分流河道微相沉积为主，受差异性沉积和成岩作用的影响，储层非均质性很强.油藏边界受控于岩石的储集能力，而物性较好的储层发育区往往发育异常高压(潘建国等，2015；唐勇等，2018).

20世纪60年代，Pennebaker(1968)通过研究威利斯顿盆地多口井的资料发现，在异常高压段纵波声波时差存在增大现象，因此他认为可以通过预测低速度异常区来预测异常高压发育区，开始出现了利用地震资料预测地层压力的研究.随后诸多学者在不同地区开展了大量的相关研究，并提出了一些预测地层压力的经典经验公式(Eaton，1972；Fillippone，1982；Martinez，1985；刘震等，1993).从1986年后，人们逐渐认识到利用有效应力定理进行地层压力预测可以提高预测的精度，由此开启了地层压力预测新的篇章(Terzaghi，1943；Han et al.，1986；Eberhart-Phillips et al.，1989).受地震资料和储层预测方法的限制，学者们主要研究纵波速度与地层压力的关系，研究发现地层压力的增大会引起纵波速度的降低，因此通过预测纵波速度的低速带可以预测可能的异常高压发育区(邵新军等，2000；薛冈等，2004；罗晓容，2004；张卫华等，2005；刘爱群等，2015).近年来，随着非常规油气勘探的需求和叠前储层预测技术的进步，越来越多的学者开始关注地层压力预测技术，并相继开发了大量的经验公式和理论模型.其中：Sayers等(2002)针对墨西哥湾地区，提出先利用共成像点道集层析成像资料建立高精度速度模型，再利用横波速度消除岩性影响计算地层压力的方法；Niranjan等(2014)基于反演方法获得高精度的纵波阻抗，并通过迭代优选的方法改进了压力预测模型，该模型在Sigsbee Escarpment地区的盐下地层中取得良好的应用效果.在该论文中，作者也指出联合多参数(包括声波阻抗、剪切模量和密度等)先消除岩性影响后再开展压力预测是未来的一个重要发展方向.在国内，也有很多学者在页岩气和碳酸盐岩油气藏等多个领域开展了地层压力预测技术的研究工作(张冰等，2014；李奎周等，2018；胡华锋等，2018；林正良等，2021).随着人们逐渐认识到横波速度的重要性，越来越多的方法将纵波速度和横波速度联合起来预测地层压力.在不同的地区，许多国内学者基于研究区测录井资料对地层压力与弹性参数之间的关系进行了拟合，得到了一系列经验公式，其中还包括了诸多利用纵横波速度以及密度联合预测地层压力的关系式.已有研究表明，根据这些经验公式在不同地区开展压力预测，均取得了很好的效果(冯福平等，2009；时梦璇等，2020).在页岩的地层压力预测中，Pervukhina等(2013)提出了一种基于岩石物理模型构建正常压实趋势线的方法，该岩石物理模型为Clay-Plus-Silt(CPS)模型，利用该模型可以提高地层速度的预测精度，从而为提高压力预测精度奠定基础.考虑到利用地震资料获得的速度值可能无法满足地层压力预测的要求，张冰和徐嘉亮(2020)提出了一种从角度域共反射点道集出发，直接通过将角道集剩余曲率作为自变量计算地层压力系数的方法.从国内外学者对压力预测方法的探讨和应用中，我们可以发现提高地层压力预测精度主要需要关注以下两点，一是如何获得高精度的速度资料(张艳伟等，2021)，二是如何建立多参数地层压力预测模型，以消除岩性和流体等其他因素的影响，获得地层压力与弹性参数之间的关系.

基于有效应力定理的地层压力预测模型由于不依赖于压实趋势校正，被国内外学者认为是适用性最广且精度最高的.由于有效应力定理是Terzaghi(1943)针对疏松的含水饱和土壤提出的，在该定理中有效应力系数为1，而非均匀介质中，有效应力受岩石特性的影响会发生变化，这些影响因素包括：岩石的体积、孔隙度、含水饱和度、流体性质、骨架所占的体积、电导率和渗透率等(Berryman，1992，1993)，所以在非均匀介质中有效应力系数往往不能为1.人们为了获得准确的岩石有效应力系数，已经开展了很多理论推导和实验研究(Nur and Byerlee，1971).Brandt(1955)在20世纪50年代最先证实地震速度与有效应力系数之间是有关系的.随后，Gurevich(2004)在理论上推导证实，当岩石由单一矿物组成且孔隙中的流体不受压力影响时，有效应力系数为1，同时他也指出，这个结论不适用于非均质岩石.很多学者也通过岩石物理实验计算了有效应力系数的值，其结果存在两种情形，即有效应力系数近似等于1(Hicks and Berry，1956；Wyllie et al.，1958)和有效应力系数小于1(Banthia et al.，1965；Todd and Simmons，1972；Hornby，1996；Sarker and Batzle，2008).这些研究数据表明，当实验样品孔隙度较高时，有效应力系数的值接近于1，而当实验样品的物性变差后，有效应力系数将低于1(Yu，2015).

利用地震资料在玛湖凹陷斜坡区三叠系低渗透砂砾岩储层中开展地层压力预测的研究时，我们分析认为该地区异常高压不是由不均衡压实作用引起的，因此选择基于有效应力定理的预测模型.为了提高压力预测的精度，本文作者曾结合胡克定律与波动方程推导了纵横波速度联合计算有效应力的方法(王斌等，2015).该地区的有效应力系数利用Todd和Simmons(1972)提出的基于岩石物理实验的计算方法获得，通过以上改进大大提高了研究区的压力预测精度(Wang et al.，2019).近年来，通过分析研究区砂砾岩样品的岩石物理实验结果和Todd法有效应力系数计算方法发现，Todd法主要利用纵波速度随地层压力和围压的变化规律来计算有效应力系数，而研究区的岩石物理实验结果表明，在超压条件下，与纵波速度相比横波速度随有效应力变化的影响因素更少，与有效应力的关系更直接.为此，本论文提出了联合纵横波速度来计算有效应力系数的方法.

1 玛湖斜坡区地质背景及异常高压成因规律分析

通过对准噶尔盆地西北缘玛湖凹陷二三叠系沉积环境、构造背景(图1)以及地化指标的分析，初步认为玛湖斜坡区异常高压的分布受“封闭条件、构造挤压、晚期高熟油气充注”三要素的控制.

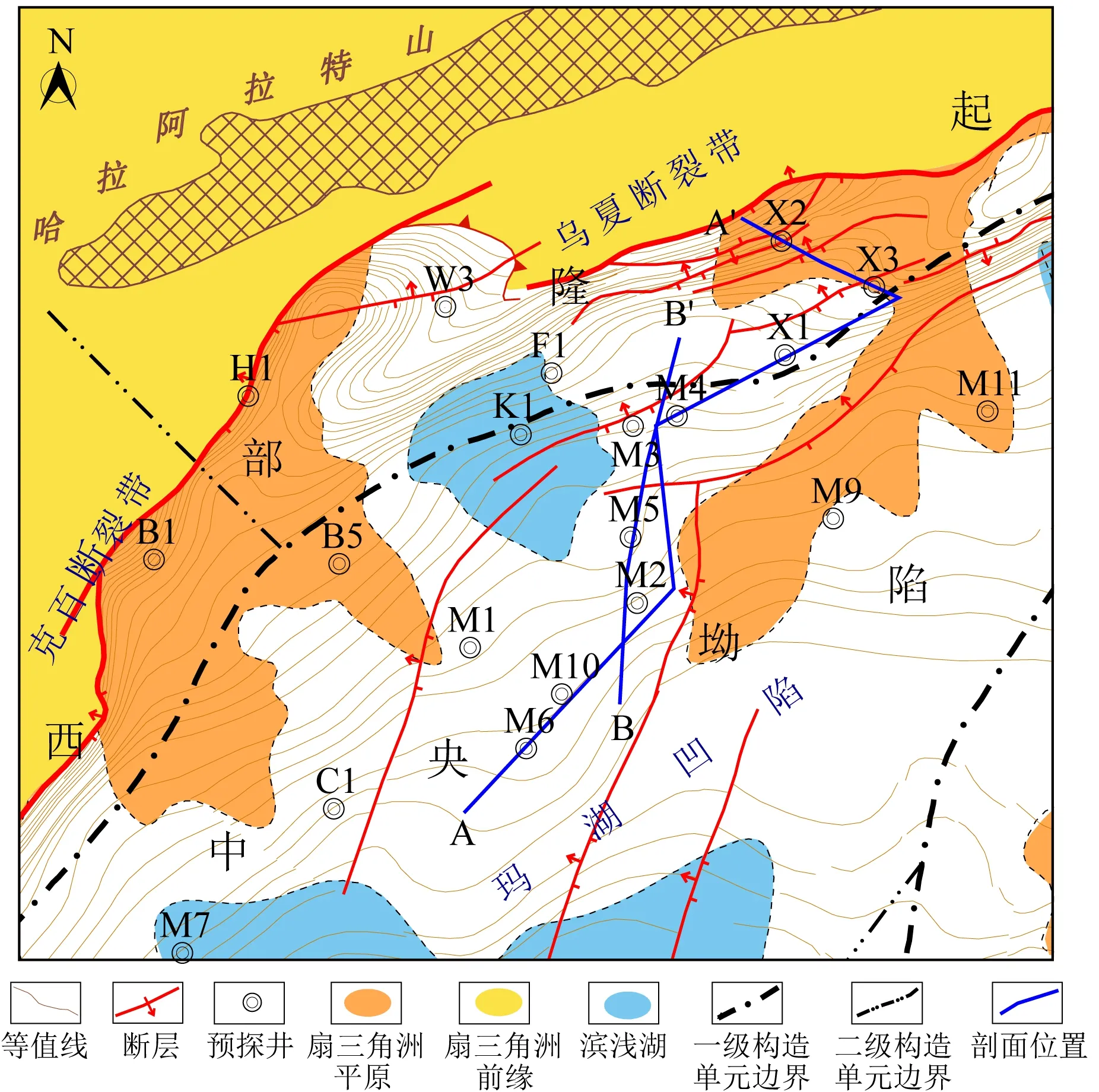
图1 玛湖凹陷斜坡区三叠系沉积相图Fig.1 The sedimentary facies map of Triassic in slope area of Mahu Sag

通常，只有当封堵条件较好而孔隙中流体无法顺畅流动方会产生局部的异常高压分布区，也就是说，一个相对封闭的环境是异常压力产生的必要条件.通过统计玛湖斜坡区和断裂带钻井的地层压力系数情况，我们发现在斜坡区钻井的地层压力系数一般较高(大于1.3)，而在断裂带钻井的地层压力系数在1左右，即为常压.从断裂带到斜坡区的连井剖面显示(图2)：(1)由于三叠纪中晚期玛湖凹陷的可容空间较大而物源供给不足，因此斜坡区的沉积物以泥岩或砂质泥岩等粒度较细的岩性为主；而断裂带由于离物源较近，沉积物主要以砂砾岩或粗砂岩等粒度较粗的岩性为主，且粗粒沉积物的厚度较大；(2)斜坡区M4、M2和M6等井在三叠系中晚期油气显示差，而断裂带的X2和X3等井与之相反，在三叠纪中晚期油气显示好，并已经成藏.由此推测，斜坡区的封闭条件要好于断裂带，在斜坡区更易于形成异常高压发育带.另外，在玛湖凹陷斜坡区因构造挤压形成的局部隆起部位也容易产生异常高压，其原因为：随着埋深的增大，地层所承受的围压也越来越大，因此由沉积作用形成的地层压力越大，而在沉积结束后构造挤压会使得地层抬升，局部的构造隆升在不造成地层破坏时，地层压力将保留.因此构造隆升地区相比同一深度的其他地区地层压力要更大，地层压力系数会更高.图3是斜坡区过玛北背斜的连井对比剖面，从图上可以看到，地层压力系数受埋深的影响较大，越往斜坡区埋深越大的区域越容易发育异常高压.与周围其他井比，因构造挤压形成的局部隆起部位，即图中M5井所在的位置，地层压力系数更高.

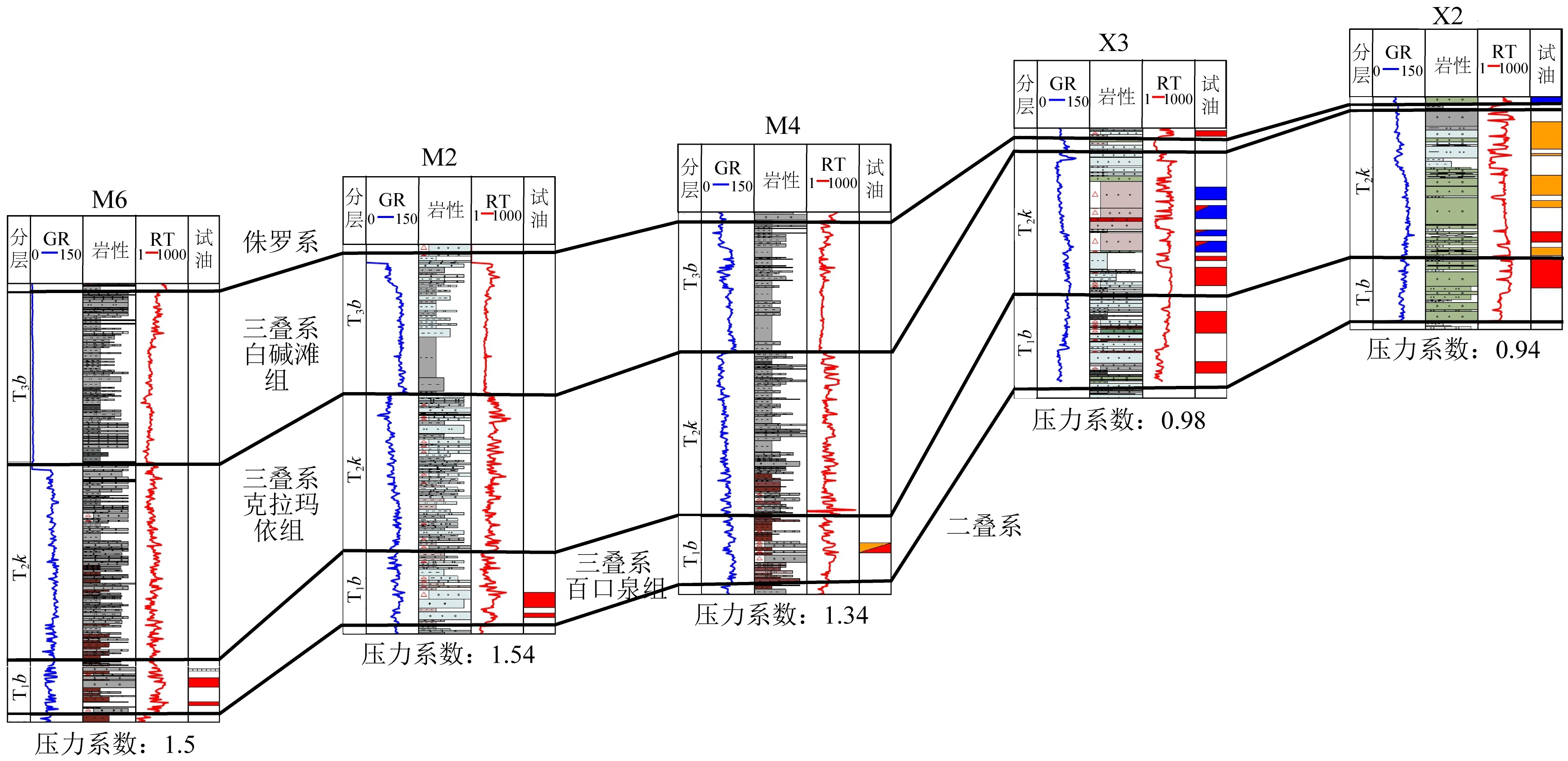
图2 过断裂带与斜坡区连井对比剖面(平面位置见图1中AA′)Fig.2 The well profile from fault zone to slope area (the plane position is AA′ in Fig.1)

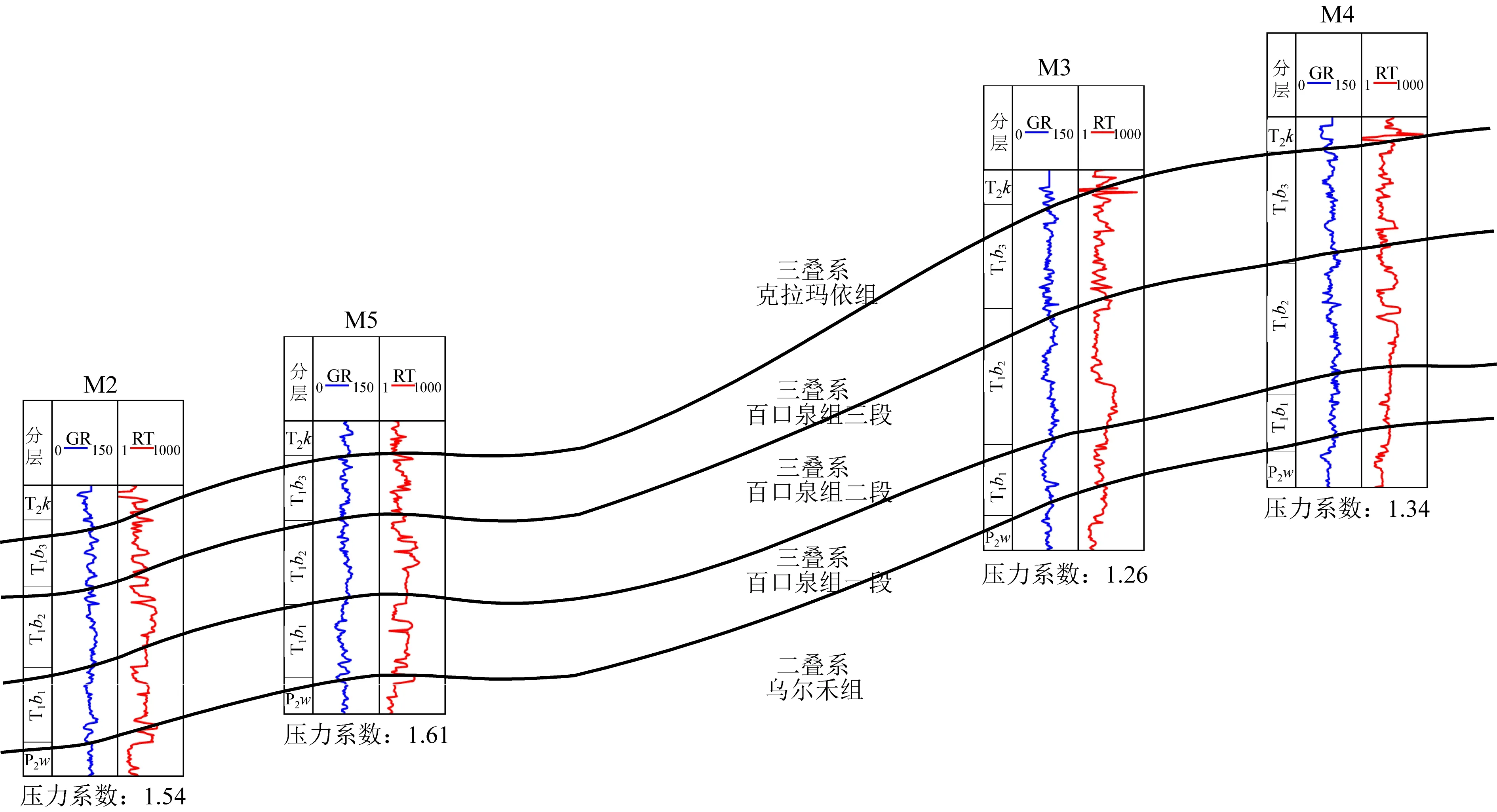
图3 斜坡区连井对比剖面(平面位置见图1中BB′)Fig.3 The well profile of slope area (the plane position is BB′ in Fig.1)

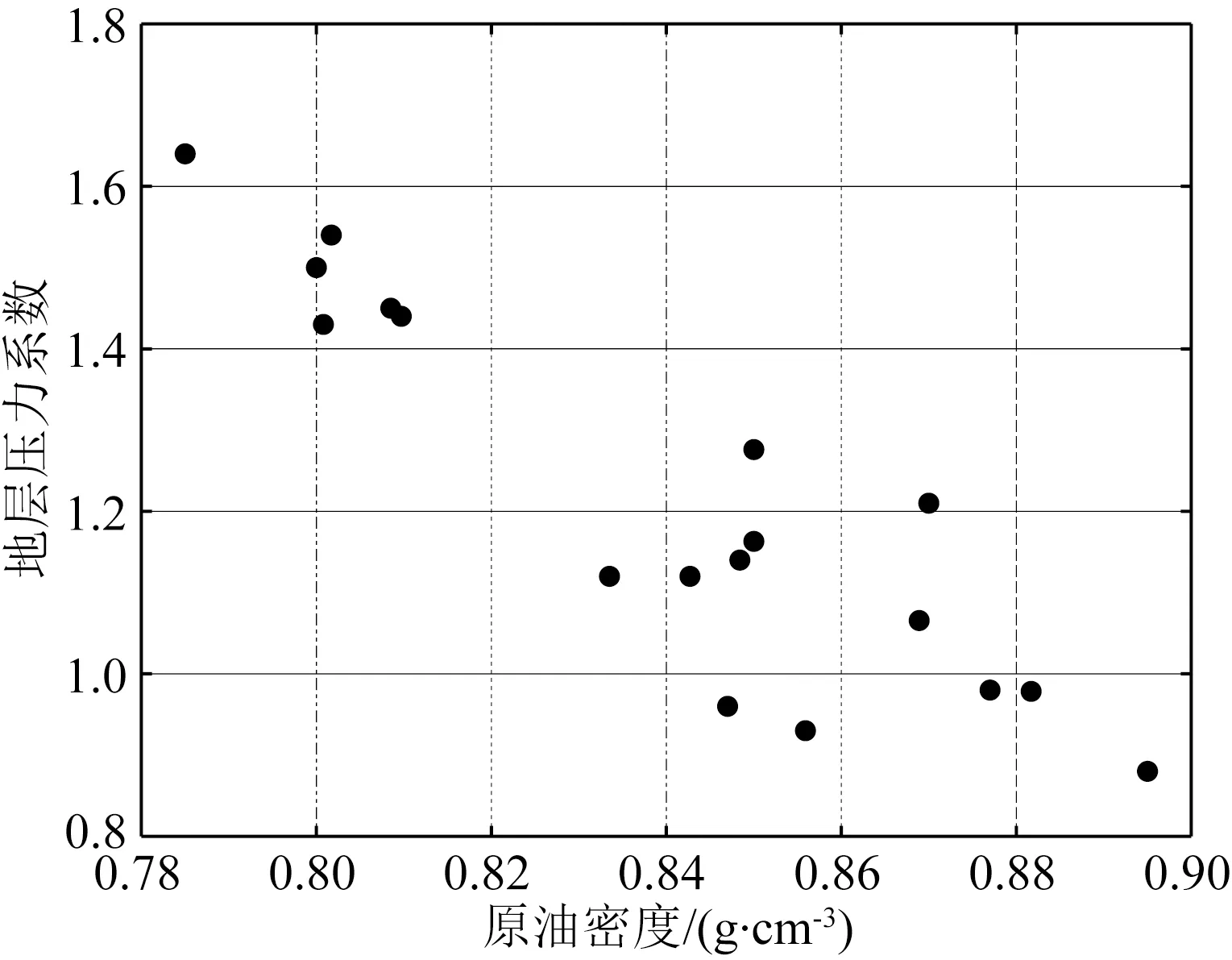
图4 玛湖凹陷斜坡区原油密度与地层压力系数交会图Fig.4 The cross-plot of the crude oil density and the formation pressure coefficient in those wells of Mahu Sag slope

2 异常高压对砂砾岩弹性性质的影响规律分析

本次研究所选用的样品为来自玛湖凹陷三叠系的碎屑岩样品.为研究异常高压对砂砾岩弹性参数变化的影响，取研究区内10口井的63块样品，在岩心洗油后对样品进行测试与分析.干燥岩样的物性参数测试结果详见附录表A1，研究区样品的孔隙度为：5.1%～13.3%，平均为8.83%；渗透率为：(0.036～76.3)×10-15m2，平均为0.605×10-15m2.许多学者对玛湖凹陷砂砾岩储层的物性特征及优质储层的形成机制进行了深入研究，研究结果均表明研究区砂砾岩储层具有典型的低孔低渗特征，优质储层主要是经历过沉积和压实后，经溶蚀作用改造形成的，储集空间以次生溶蚀孔隙为主，优质储层主要发育在长石和易溶蚀岩屑含量高的地区(瞿建华等，2017；肖萌等，2019).从前文介绍可知研究区异常高压不是由于欠压实作用形成的，因此研究区普遍发育的异常高压不能有效保护原生孔隙.为模拟实际地层条件，我们在有效应力30 MPa下利用超声实验设备测量样品的纵横波速度，并与前人研究得到的经验关系式进行对比.

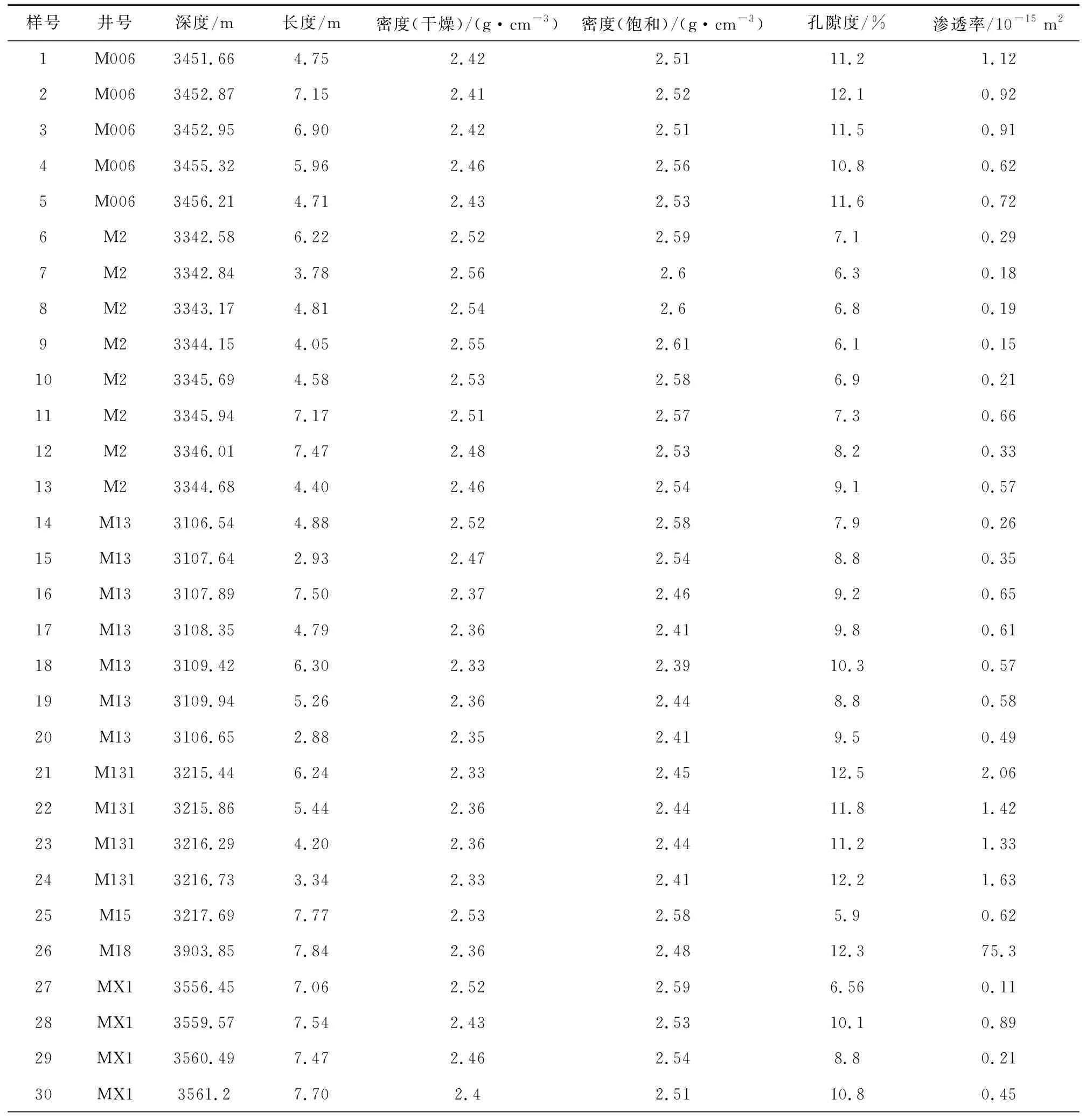
表A1 测试样品的基本物性参数Table A1 Basic physical parameters of test samples

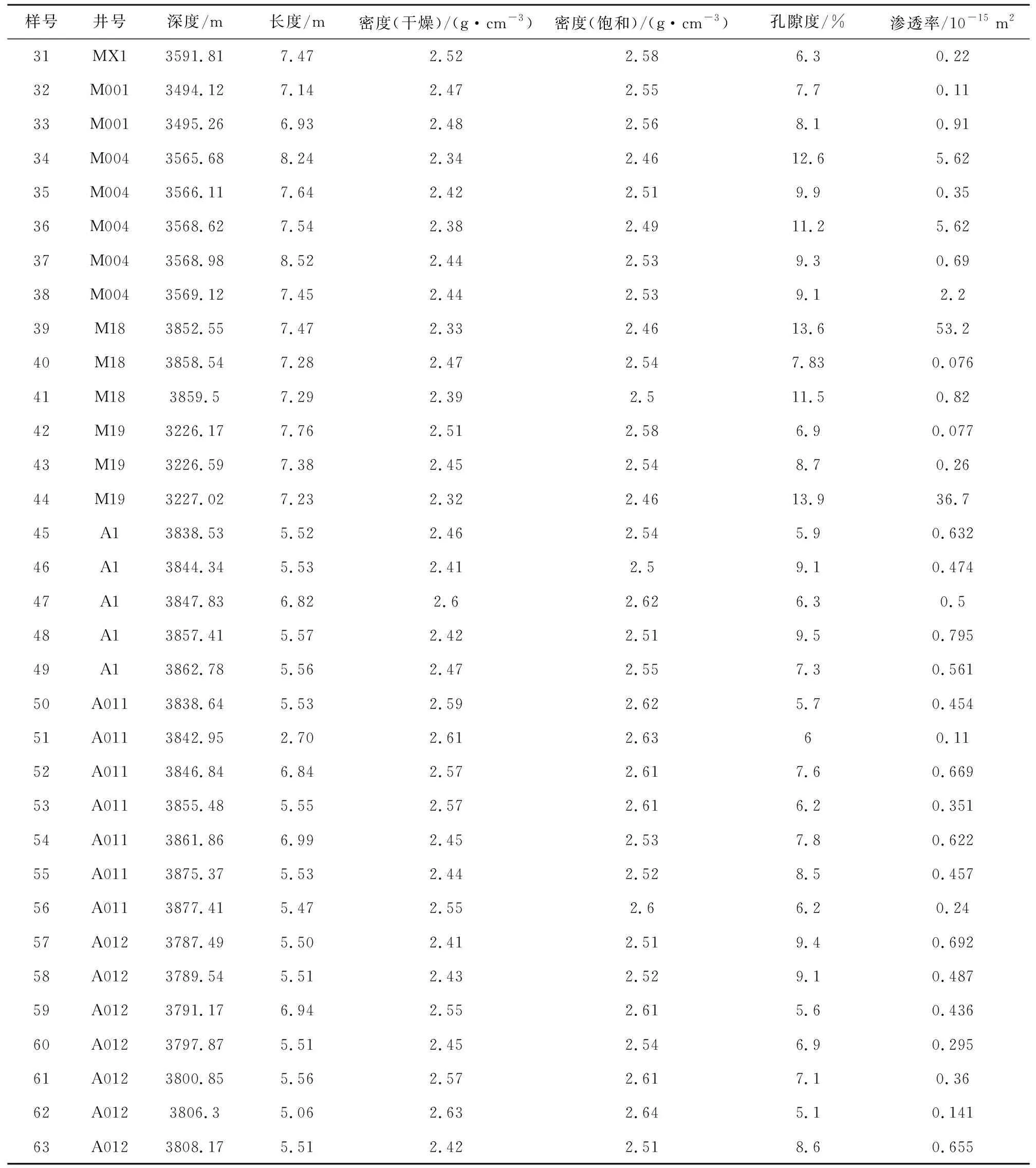
续表A1

最早的密度与速度关系由Gardner等(1973)总结不同岩性实验结果得到.根据Gardner公式，速度与密度关系的基础模型为：

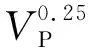
(1)

式中：ρ表示密度，单位为g·cm-3；VP表示纵波速度，单位为km·s-1.

后来，许多专家基于Gardner公式，获得了适用于不同地区的经验参数，并被广泛应用.其中，Castagna等(1993)针对不同岩性建立了不同的速度-密度关系，即：

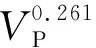
(2)

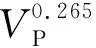
(3)

图5展示了研究区饱水样品纵波速度与密度的交会图，图中散点为实测样品点，不同颜色的曲线分别代表基于Gardner公式与Castagna砂、泥岩公式计算的结果.从图看出，实验样品数据点均落于Castagna砂、泥岩线之间，这反映了岩石样品中主要矿物组分的变化，即随样品中泥质含量的增加数据点逐渐向泥岩线移动，而随着石英含量的增加数据点向砂岩线移动.总体而言，样品点与Castagna砂岩线更为接近.另外，通过对实验数据进行拟合，可以得到研究区样品纵波速度-密度关系：

③做好河道清障工作。严禁恢复2013年洪水冲毁的违章围堤，按照《松花江流域防洪规划》相关安排，抓紧落实松花江流域干流河道围堤的退人退耕和围堤清除工作；结合灾后重建和江河治理，将河道内居住人员搬迁至安全区域。严格执行涉河项目审批制度，坚决杜绝侵占河道、私建滥建，确保河道行洪畅通和防洪安全。

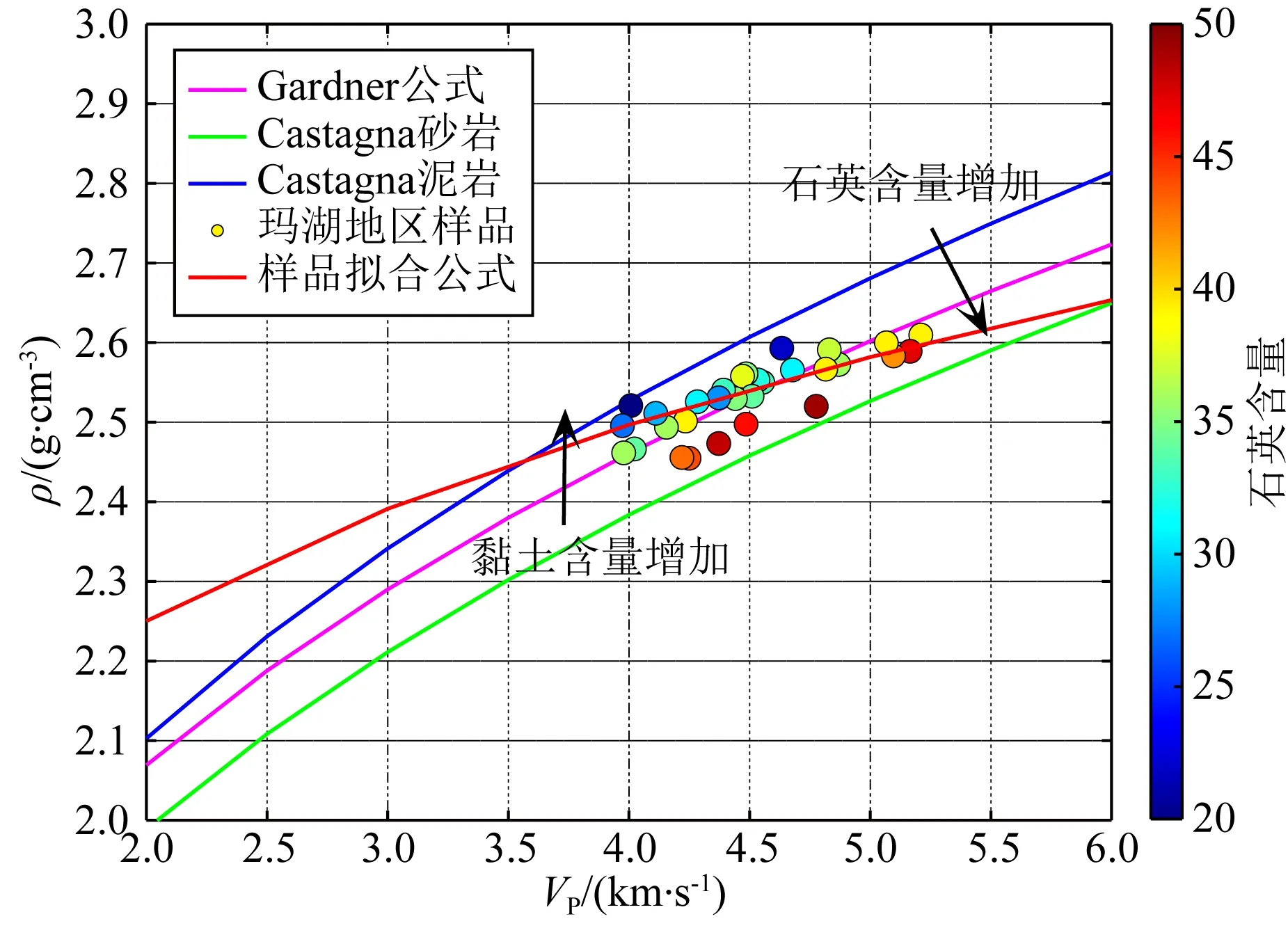
图5 研究区砂砾岩样品纵波速度与密度交会图Fig.5 The cross-plot of P-wave velocity and density of the sandy conglomerate samples in the study area

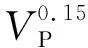
(4)

图6为有效应力30 MPa下干燥及水饱和样品的纵、横波速度交会图，图中散点为样品数据点，红色和绿色实线分别为Castagna泥岩线(Castagna et al.，1985)和李庆忠(1993)砂岩线，其中，Castagna等(1985)总结的泥岩线公式为：

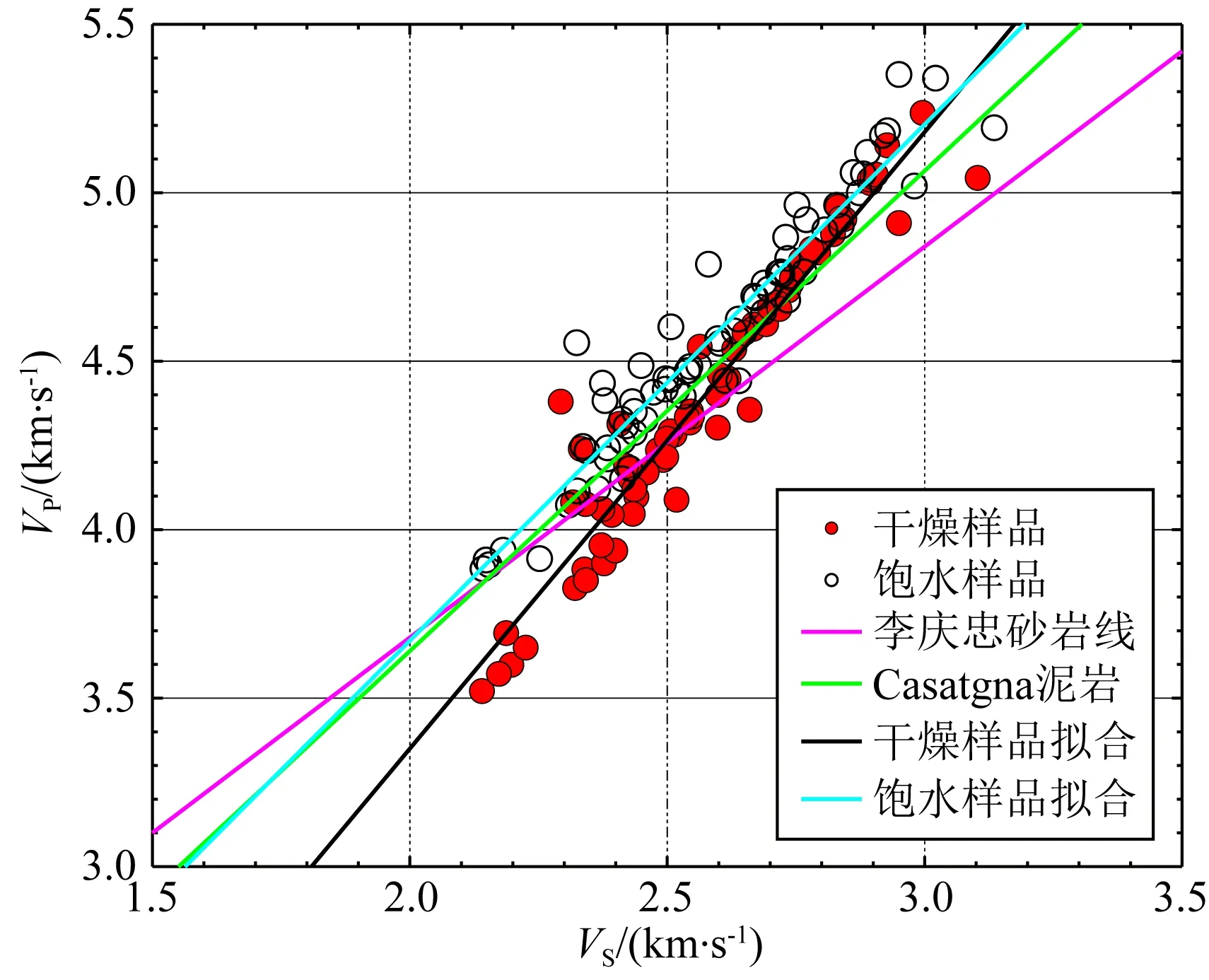
图6 研究区砂砾岩样品横波速度与纵波速度交会图Fig.6 The cross-plot of S-wave velocity and P-wave velocity of the sandy conglomerate samples in the study area

VP=1.36+1.16VS，

(5)

式中，VS表示横波速度，单位为km·s-1.李庆忠(1993)总结大量已发表的实验数据后，认为受矿物组分和孔隙中流体的影响，地下实际砂岩的纵横波关系最好采用抛物线拟合，并得到饱水条件下砂岩纵横波速度趋势线为：

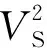
(6)

由图6可见，无论是在干燥还是水饱和条件下，纵、横波速度之间具有较好的正相关关系，但它们之间的关系又与一般的经验关系有差异.当横波速度小于2.6 km·s-1时，相同横波速度条件下，干燥样品与水饱和样品的纵波速度差异较大，按泥岩公式计算的纵波速度大于干燥样品的纵波速度，却小于水饱和样品的纵波速度；当横波速度大于2.6 km·s-1时，相同横波条件下，干燥样品和水饱和样品的纵波速度相近，按泥岩公式计算的干燥样品的纵波速度小于实验样品的纵波速度.水饱和样品的实验结果显示，在相同的横波速度时，按李庆忠砂岩线计算的纵波速度要小于实验样品的纵波速度.鉴于此，我们拟合研究区实验样品，得到在干燥及水饱和条件下，纵横波速度关系分别为：

干燥条件下：VP=-0.31+1.83VS，

(7)

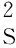
(8)

从以上对实际测试数据与已有经验公式的对比可知，研究区样品表现为密度高、纵波速度和横波速度小的特征.样品密度较大主要原因为砾石成分为密度较高的火山碎屑，而速度较小主要原因为在超压作用下，阻碍了岩石的胶结作用，岩石胶结较差，而且胶结作用对横波速度的影响更大.

为了分析异常高压对砂砾岩样品弹性参数的影响，我们设计了一组模拟孔隙超压过程的岩石物理实验.在实验室模拟超压时，主要基于有效应力定理，考虑围压，地层压力和有效应力之间的相互耦合关系.有效应力定理自提出以来经过国内外学者的不断改进，可以表述为：

σ=Pov-α·Pf，

(9)

式中：Pf为地层压力，单位为MPa；Pov为上覆地层压力(围压)，单位为MPa；α为Biot有效应力系数(Biot，1941)，无单位；σ为有效应力，单位为MPa.

Todd和Simmons(1972)提出了利用实验室中不同围压及地层压力条件下岩石物理实验测试得到的纵波速度结果计算有效应力系数的公式：

(10)

式中，VP为纵波速度，单位为km·s-1；Pf为地层压力，单位为MPa；Pd为差应力，代表围压减去地层压力后剩余的压力，单位为MPa.Pd可表示为：

Pd=Pov-Pf.

(11)

首先，固定地层压力(Pf)为0 MPa，改变有效应力(σ)，从有效应力为0 MPa开始，每隔5 MPa测量一次纵、横波速度.然后，固定围压(Pov)为60 MPa，在有效应力分别为5 MPa、10 MPa、20 MPa、…、60 MPa时各测量一次纵、横波速度；接着改变围压为70 MPa和80 MPa，重复前述操作.

图7给出了玛湖凹陷斜坡区砂砾岩样品在孔隙超压过程中的速度变化曲线.由图可见，在地层压力固定时，纵横波速度随有效应力的增加而增加(见图中绿色实线).当围压一定时，根据有效应力定理，有效应力减小地层压力将增大，这个过程中纵波速度表现出逐渐减小的趋势；在地层压力较低时纵波速度变化缓慢，但随着地层压力的增大，纵波速度的变化会越来越快，特别是当有效应力小于30 MPa以后.当有效应力一定时，地层压力随围压的增大而增大，此时纵波速度也随之增大(图7a).对于横波速度，当围压一定时，其大小随着地层压力的增大也会减小；但当有效应力一定时，地层压力的变化对横波速度的影响几乎可以忽略(图7b)，这与纵波速度的变化规律有显著区别.

图7 研究区样品孔隙超压过程中速度的变化规律(a) 纵波速度； (b) 横波速度.Fig.7 The variation law of velocity during the progress of pore overpressure in the study area(a) P-wave velocity； (b) S-wave velocity.

考虑到研究区样品的埋深在3300～4000 m左右，上覆岩石的平均密度约为2.55～2.61 g·cm-3，因此实验室模拟模拟地层条件上覆地层压力时所用的围压应为70～90 MPa，正常地层压力的变化范围在30～40 MPa.为了观察不同速度随地层压力的变化情况，我们定义速度的变化率为：

(12)

式中：V表示岩石物理实验观测到的速度，单位为km·s-1；V0表示地层压力为0 MPa时的速度，单位为km·s-1.图8a为研究区样品在80 MPa围压下，纵横波速度变化率随地层压力变化的曲线，从图中可知，随着地层压力的增大，纵横波速度的变化率都会增大，但横波速度的变化率比纵波速度的变化率更大.图8b为80 MPa围压下，纵横波速度比随地层压力变化的曲线，观察该曲线的变化情况可以发现，随着地层压力的增大，纵横波速度比会增大.依据实验结果在固定围压时，随着地层压力的增大，当产生异常高压后，横波速度的变化相对于纵波速度更为明显.

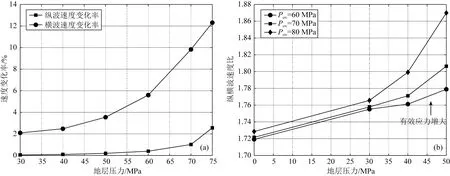
图8 研究区样品速度变化率及纵横波速度比随地层压力的变化规律(a) 速度变化率； (b) 纵横波速度比.Fig.8 The variation law of velocity variation rate and the ratio of VP and VS with the pore pressure in the study area(a) Velocity variation rate； (b) The ratio of VP and VS.

3 基于岩石物理实验改进的有效应力系数计算方法

鉴于前文分析认为横波速度是地层压力的敏感参数，且有效应力是指上覆地层压力作用在骨架上的部分，因此为了提高计算研究区样品有效应力系数的精度，本文借鉴Todd有效应力系数计算方法的经验，设计了一组实验改进了公式(10).即分别测量在地层压力为0 MPa时和差应力分别为5 MPa、10 MPa、20 MPa、30 MPa和40 MPa时不同围压条件下砂砾岩样品对应的纵波速度和横波速度，测量结果如图9所示.图中不同颜色的曲线分别表示不同差应力条件下的实测纵横波速度，详见图9图例.公式(10)在计算有效应力系数时，仅用到了纵波速度的实验结果.当围压增大时，被测样品的结构会跟随发生变化，因此在地层压力为0时，纵波速度随围压的变化不仅仅是由差应力的变化引起，有可能孔隙的变化也会造成纵波速度的变化，而横波速度相对纵波来说这种影响要小.所以本文在计算有效应力系数时，引入横波速度的测试结果，提出了一种纵横波速度联合计算有效应力系数的方法：

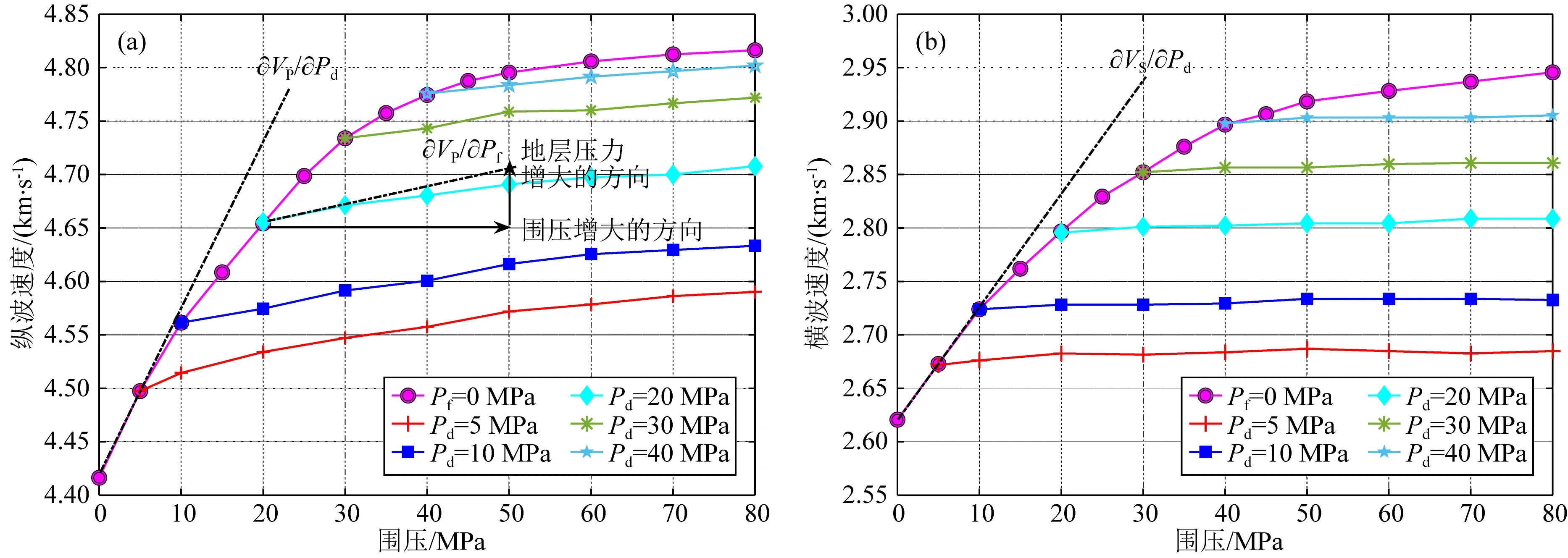
图9 不同围压条件下研究区砂砾岩样品的纵横波速度(a) 纵波速度; (b) 横波速度.Fig.9 Velocity as a function of confining pressure for samples of the study area(a) P-wave velocity; (b) S-wave velocity.

(13)

式中：VS为横波速度，单位为km·s-1；∂VP/∂Pf为差应力固定时纵波速度随地层压力变化曲线的斜率；∂VS/∂Pd为地层压力为0时横波速度随差应力变化曲线的斜率；两者均由岩石物理实验数据获得.

在玛湖地区，我们分别用Todd法和本文提出的方法了有效应力系数，并利用两种方法计算的有效应力系数分别预测了地层压力系数.图10a为两种方法计算的有效应力系数与孔隙度的交会图，从图中观察可知，与Todd法计算的有效应力系数相比，本文改进后预测的有效应力系数具有如下特点：(1)新方法计算得到的有效应力系数值小于Todd法得到的有效应力系数值；(2)对于孔隙度较大的情形(即当储层物性较好时)，两种方法计算的有效应力系数基本一致，且值趋近于1，这与前人研究认为在物性较好条件下有效应力系数值近似等于1相吻合；(3)两种不同方法计算的有效应力系数与孔隙度都具有正相关关系.在孔隙度较小的区间，两者存在较大差异，如在玛湖地区甜点储层孔隙度区间(即孔隙度大于8%时)，Todd法计算的有效应力系数范围为：0.7～0.9，而新方法计算的有效应力系数范围为：0.3～0.7，如果套用原来计算方法得到的有效应力系数值会对地层压力的计算精度有影响.图10b为利用两种方法预测的地层压力系数与真实地层压力系数的交会图，图中横坐标为真实地层压力系数(MTS实际测试资料)，纵坐标为预测的地层压力系数.与真实压力系数相对比，新方法预测的地层压力系数精度更高，与真实的压力系数具有更好的相关性，而利用Todd法预测的地层压力系数普遍偏小，而且预测结果较发散.

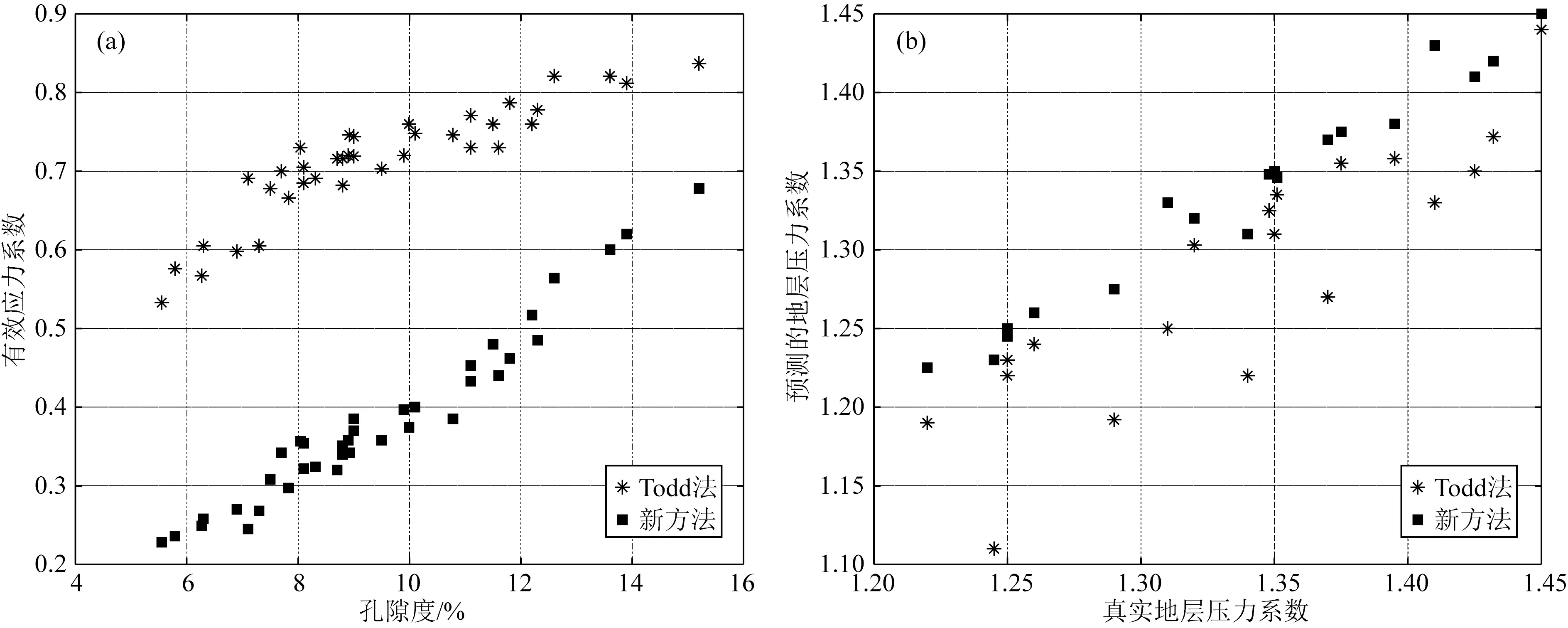
图10 不同方法计算的有效应力系数对比图(a) 孔隙度与有效应力系数交会图; (b) 真实地层压力系数与预测地层压力系数交会图.Fig.10 The effective stress coefficient calculated by different methods(a) The porosity and the effective stress coefficient; (b) The real and predicted formation pressure coefficient.

4 应用实例

4.1 玛湖凹陷斜坡区单井压力预测

在玛湖凹陷斜坡区M3井区，我们通过M3井岩石物理实验结果，利用公式(10)、(13)分别计算获得的有效应力系数为0.78和0.63.图11为验证井M2的地层压力预测结果，从图中可知，在M2井侏罗系以上地层中地层压力系数为1，而进入三叠系后地层压力逐渐增大，在三叠系百口泉组地层压力达到最大，压力系数接近1.6.利用公式(13)的预测结果要比公式(10)的预测结果更接近MDT实际测试数据.

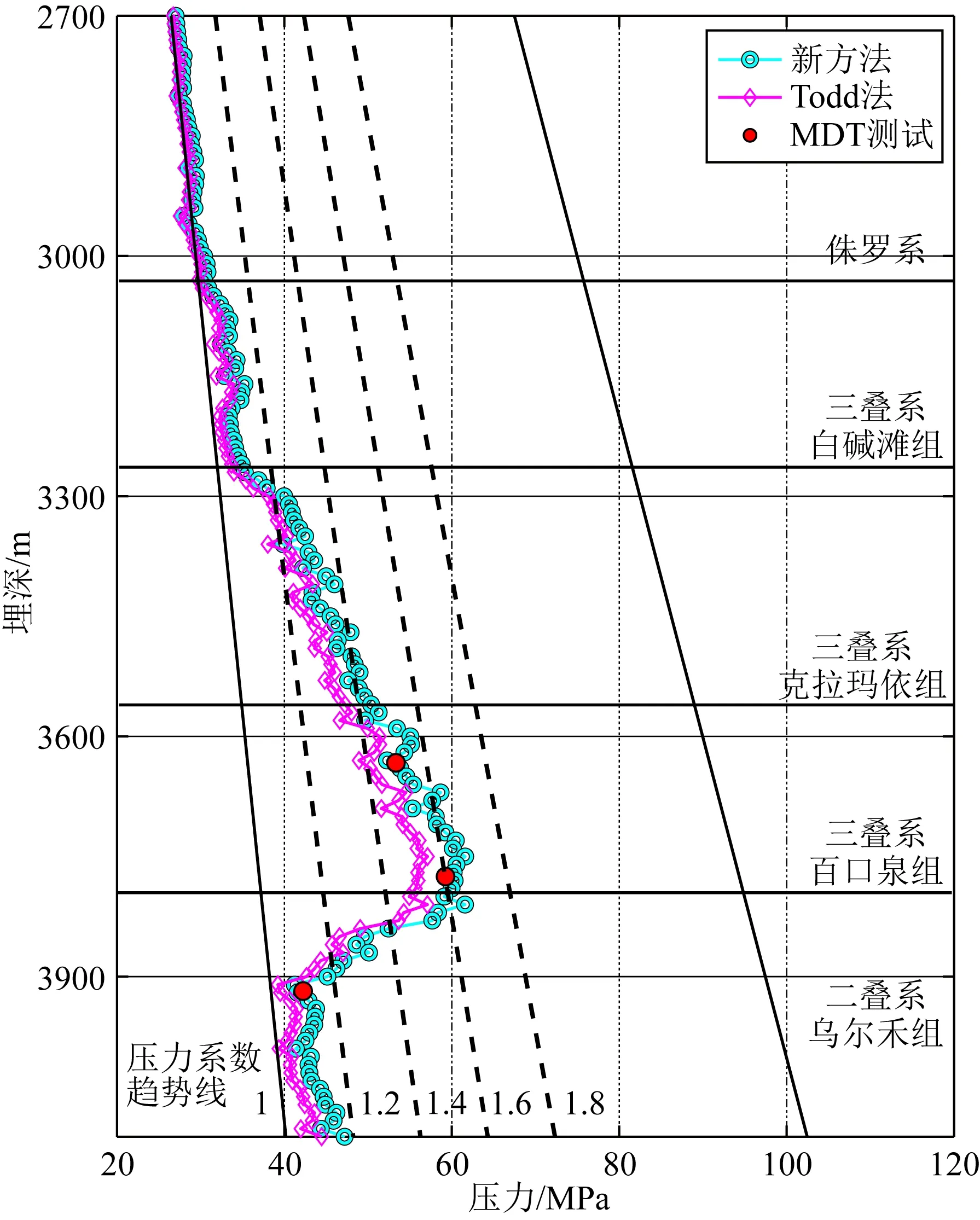
图11 玛湖凹陷斜坡区M2井单井地层压力预测图Fig.11 Test for formatin pressure prediction of well M2 in Mahu slope

4.2 玛湖凹陷斜坡区平面压力预测

在玛湖凹陷斜坡区选择在M131井区将前文提出的新有效应力系数计算方法代入到有效应力定理中，并利用反演得到的纵横波速度联合预测M131井区地层压力，预测结果如图12所示.图中色标代表地层压力系数的大小，其中红黄色代表高值，蓝绿色代表低值.从图中可以看出，预测结果与已钻井资料基本一致，且异常高压区与甜点储层发育区(图中黑色点划线圈定的范围)吻合效果也较好，由此进一步证实新模型在地层压力预测中的可靠性和适用性.鉴于此，利用该结果可对研究区下一步的井位部署提供重要依据.由于实际钻探结果及多位学者的研究认识证实，在玛湖地区当压力系数大于1.3后钻井的产能有较大的提高，且压力系数大于1.3的地区与有效源岩的发育区也较吻合(雷德文等，2014；李军等，2020).为此分析预测结果，发现研究区压力系数大于1.3的区域共有81 km2，除了已钻探证实的工区西北部的M131井区外，工区西南部的M2井以南、东部的M002井以东A5井以西地区均为研究区内的有利勘探区.

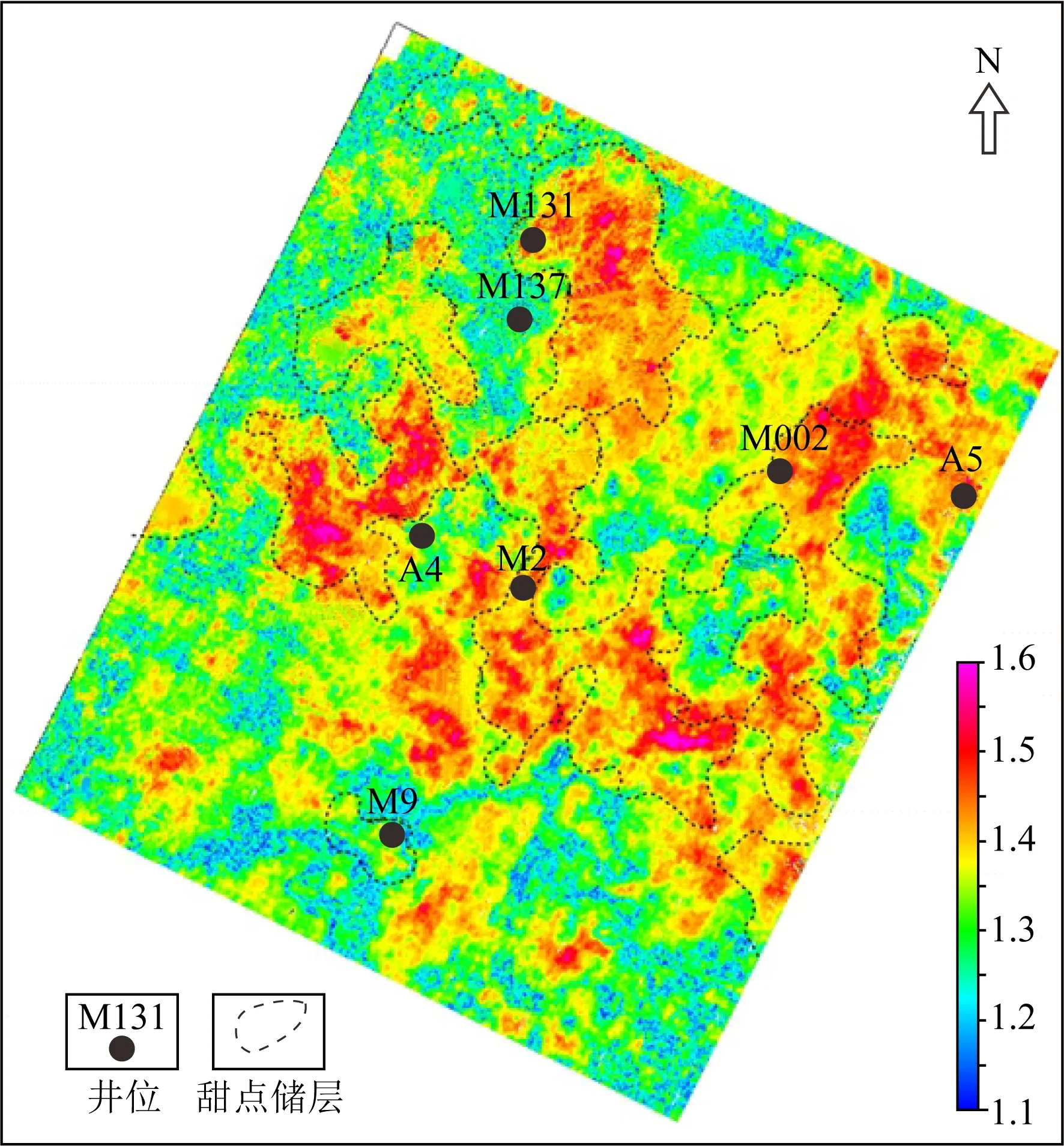
图12 利用新方法预测的M131井区压力系数分布图Fig.12 The map of pressure coefficient distribution predicted by novel method in the M131 area

5 结论与认识

通过对准噶尔盆地玛湖凹陷砂砾岩储层中广泛发育的异常高压形成机理的分析以及模拟地层超压过程的岩石物理实验，我们系统分析了研究区异常高压对岩石弹性性质变化规律的影响.分析实验结果可知，当有效应力不变时，横波速度不随围压的改变而改变，而纵波速度会随着围压的增大而增大，鉴于此，我们在计算有效应力系数时用横波速度随差应力的变化率替换了纵波速度随差应力的变化率，改进了压力预测模型，提高了压力预测的精度.通过分析玛湖凹陷斜坡区砂砾岩储层的岩石物理实验得到的结论如下：

(1)异常高压的存在会阻碍岩石的胶结作用，致使岩石的胶结变差，进而会影响岩石纵横波速度的变化规律.受异常高压的影响，玛湖凹陷砂砾岩储层的纵横波速度小于Castagna砂岩线和李庆忠砂岩线等经典砂岩的纵横波速度.另外，异常高压对样品横波速度的影响要大于对纵波速度的影响.

(2)在物性较差的岩石中有效应力系数的值会小于1，可以利用岩石物理实验计算得到有效应力系数.而在计算有效应力系数时，分析纵横波速度随有效应力和围压的变化规律可以有效提高计算有效应力系数的精度.

研究结果表明，综合利用纵横波速度联合预测异常高压带是利用地震资料预测地层压力的一条有效途径，具有重要的理论意义和实际应用价值.本预测方法主要是结合研究区实际的岩石物理测试来确定有效应力系数提高了地层压力预测的精度，在其他类似工区开展类似研究时，可以借鉴该方法，通过相应的岩石物理分析，减少其他因素对纵横波速度的影响，建立相应的有效应力系数计算模型，提高利用地震预测地层压力的精度.

附录