利用最小平方基准面延拓压制自由表面多次波I:海底观测地震数据
朱峰, 程玖兵
同济大学海洋地质国家重点实验室, 上海 200092
0 引言
主动源海洋地震方法广泛用于海洋地质调查、油气与天然气水合物勘探以及海底壳幔结构与动力学研究.海洋地震数据的采集方式主要分为海面拖缆观测和海底观测两大类,其中后者包括海底电缆(OBC)、海底节点(OBN)和海底地震仪(OBS)等三种形式.海底检波器一般由声压检波器(水检)和三分量质点振动速度或加速度检波器(陆检)组合而成,所接收的四分量(4C)信号较完整地记录了地震波三维矢量振动信息,既有利于联合纵、横波改善构造成像、岩性区分和流体识别,又为从海底观测记录分离上-下行波、P/S波创造了有利的数据条件.
由于存在强阻抗反差的气-液自由表面和固-液海底界面,海底多分量地震数据波场十分复杂,且发育多种形式、不同阶次的表面多次波,给基于一阶散射理论的常规地震偏移成像或速度反演方法带来极大的困扰.因此,在海洋地震数据处理过程中,压制表面多次波一直是非常关键的环节.传统方法要么根据多次波的周期性或者在某种变换域与一次波能量分布差异进行去除,如预测反褶积法(Peacock and Treitel,1969)、F-K滤波法(Ryu,1982)、Radon变换法(Foster and Mosher,1992)、聚束滤波法(胡天跃和王润秋,2000)以及扩展成像道集上压制多次波的方法(Wang et al.,2014)等.要么采用基于波动理论的预测相减法,如模型驱动的波场外推法(Loewenthal et al.,1974)、数据驱动的反馈迭代法(SRME)(Berkhout and Vershuur,1997)和逆散射级数法(Weglein et al.,1997).近年来,以WRW传播模型为正演引擎,在经典的SRME方法基础上发展出了压制多次波的稀疏反演法(EPSI)(van Groenestijn and Verschuur,2009a,b;Lin and Herrmann,2013).
自由表面多次波可视为等效面源产生的一次波,比实际点源产生的一次波有更宽的地下照明,可以在地震成像与反演中加以利用(刘伊克等,2018;刘学义等,2021b).如图1所示,若按照等时原理对多次波进行成像,延拓过程中的上、下行波可能按非物理的波路径相遇,会在错误的位置形成假象.随着多次波阶数增加,这些非物理串扰会更多、更复杂.若能把多次波分阶提取出来,k阶多次波作为源端波场进行正传,k+1阶多次波作为检波器端波场进行反传,二者的零延迟互相关也可构建地下反射界面或散射点的图像(刘学建和刘伊克,2016;叶月明等,2019;Liu et al., 2020).此外,相邻阶次多次波之间的互相关可以重构一次波信号(Verschuur and Berkhout,2005;Yu and Schuster,2002;Wapenaar,2006).不过,这些方法的实际应用一直受多次波分阶提取精度的制约,而且不同阶次多次波成像结果很难自适应叠加.
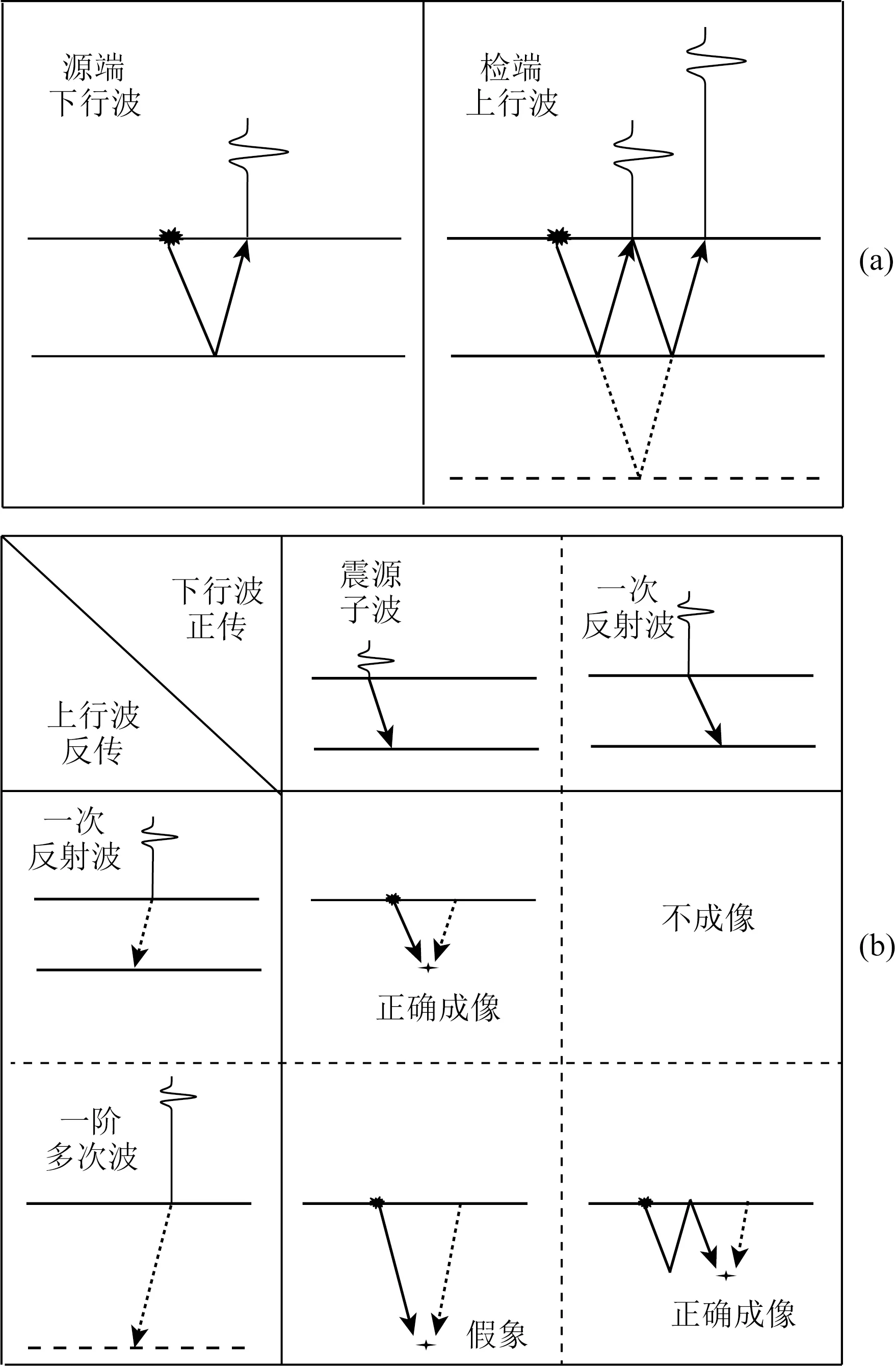
图1 一次反射波与一阶多次波联合成像示意图(a) 源端与检波器端的输入地震数据; (b) 互相关成像.Fig.1 Schematic diagram of imaging the primary and first-order multiple reflections(a) Input data at source- and receiver-sides; (b) Imaging via cross-correlation.
迄今为止,处理表面多次波的方法已经很多,但都有各自的优势与不足,尤其是对海底观测地震数据的适应性不足(Verschuur and Neumann,1999;刘国昌等,2013;张广利等,2016).若按产生的位置或时间先后,可把表面多次波分为源端多次波(包括源端鬼波)和检波器端多次波.在理想情况下,海底声压分量(P分量)和质点速度垂直分量(Z分量)记录到的下行波极性相反,上行波极性相同,据此进行的PZ叠加或PZ相减可经上-下行波分离压制检波器端的表面多次波.依据更复杂的弹性波场分离方法,还可在检波器端上-下行波分离基础上实现P/S波模式解耦(Amundsen et al., 2000; Muijs et al., 2004).然而,在实际应用中,这些波场分离方法需考虑检波器在海底的耦合情况和水检-陆检仪器响应差异对多分量数据进行校正或标定,甚至还需要估计海底介质参数,这就加大了海底观测数据多次波压制的难度(刘学义等,2021a).在最小二乘理论框架下,把源端正传的下行波场与检波器端反传的上行波场进行迭代反演成像,可以逐步压制非物理的串扰假象,实现一次波和多次波联合成像(Berkhout and Vershuur, 1994; Whitmore et al., 2010;Zhang and Schuster,2014;Wong et al., 2015; Lu et al.,2018).该类方法虽无需分阶提取多次波,但需在观测面上分离上-下行波,或者分离出一次波与多次波.
为了避免多次波分离或分阶提取面临的繁琐而又困难的工作,本文结合地震干涉原理(Bakulin and Calvert,2006;Schuster,2009),借鉴最小平方基准面延拓(LSR)理论框架(Ferguson,2006; Xue and Schuster,2008;Zhu et al., 2020;Zhu and Cheng,2022),通过迭代反演实现多次波向一次波的转化,从而消除自由表面和海水层对海底地震记录的影响.本文首先,通过卷积型互易定理推导实际波场状态与去除自由表面和上覆介质影响的理想波场状态之间的数学物理关系,建立基准面虚拟观测数据同实际观测数据之间的正演方程.然后,结合海森算子和点扩散函数揭示常规干涉法基准面延拓的不足,进而提出基于最小平方反演的基准面延拓方法,并将其用于压制OBC/OBN数据中的表面多次波.最后,通过理论模型合成数据实验证实方法的有效性.
1 考虑自由表面效应的最小二乘基准面延拓方法
1.1 正问题
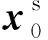
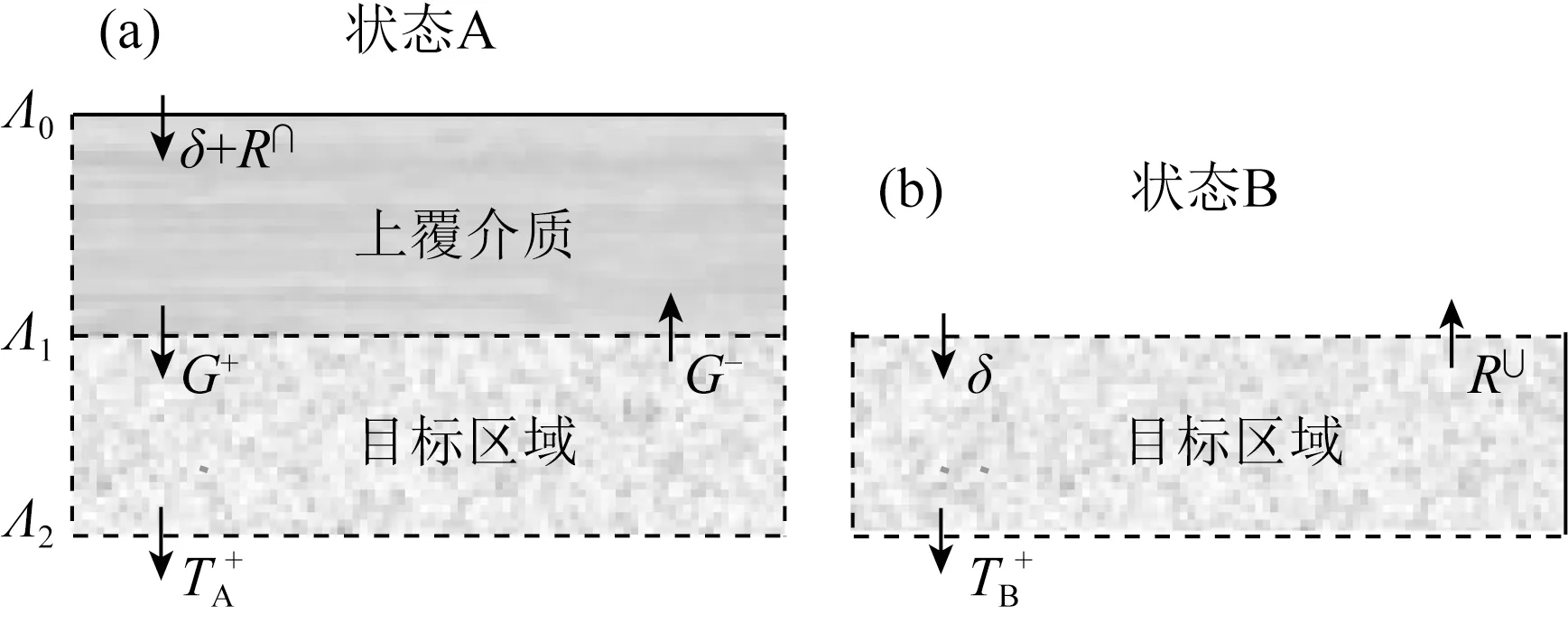
图2 两个独立的波场状态(a) 真实状态; (b) 理想状态.Fig.2 Schematic diagram oftwo wave field states(a) Real state; (b) Ideal state.
根据附录A,按照单向波互易定理揭示的传播不变性(Wapenaar et al., 2004),可以推导出:
(1)
如图3,假定在地面或海面激发震源,在基准面Λ1(如海底或水平井)布放检波器进行观测.利用关于R∪的炮检互易性(Wapenaar,2004),上式可改写为
(2)
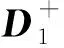
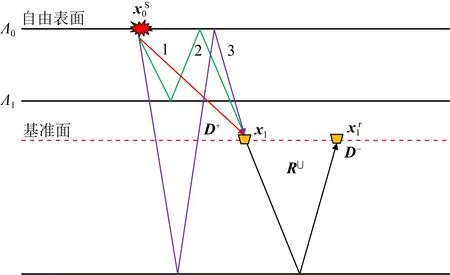
图3 受自由表面和上覆介质影响的地震观测示意图Fig.3 Illustration of seismic observation with the effects of free-surface and overburden medium
1.2 基于干涉原理的基准面延拓
本文基准面延拓的目的是从实际观测记录中重构不受自由表面和上覆介质影响的、来自目标区域的反射或背向散射信号R∪(见图3黑色波路径).如图4,方程(2)描述的时间域多维褶积⊗对应频率域乘积运算,可写成如下矩阵形式:
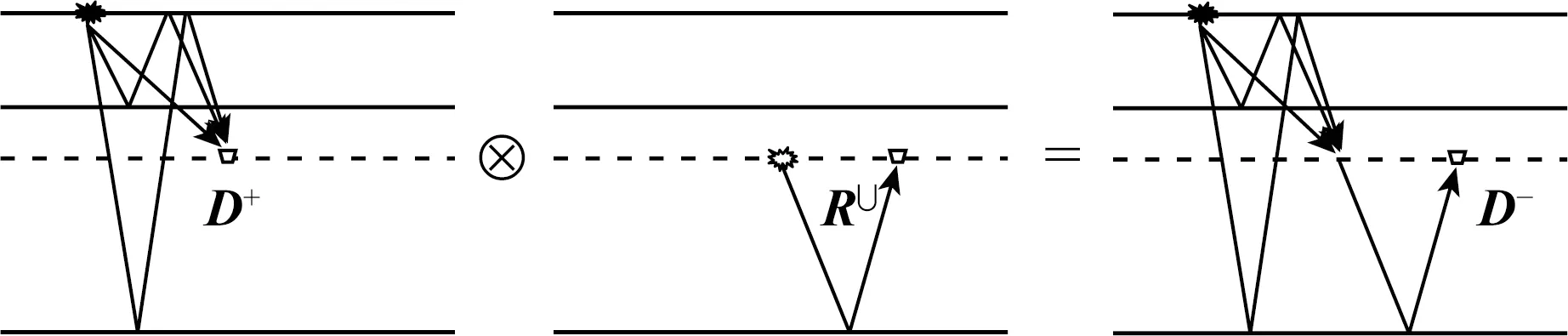
图4 多维褶积地震干涉正演模拟示意图Fig.4 Schematic diagram of forward modelingusing multi-dimensional convolution based on seismic interferometry
D-=D+R∪.
(3)
按照地震干涉理论,公式(2)或(3)可利用稳相积分原理进行解释(Schuster,2009).对观测数据施加D+的逆算子,可获得虚拟观测数据:
R∪=[D+]-1D-.
(4)
这个反问题的直接求解依靠大型矩阵D+的显式求逆,在实际应用中很难操作.传统方法一般以伴随算子D+*(*表示复共轭转置)代替其逆算子,即:
R∪′=D+*D-.
(5)
如图5,一旦在实际观测面分离出上、下行波信号,通过(5)式表达的多维互相关,可在一定程度上消除它们在源端的共同波路经,通过干涉叠加构建任意两个检波器之间的格林函数场.若把参与互相关的两个检波器中的一个视为虚拟震源,对整个实际观测数据如此的干涉叠加最终获得所谓的虚拟观测记录.这种基于干涉原理的基准面延拓方法也被称为虚源法(Bakulin and Calvert,2006;Schuster,2009).
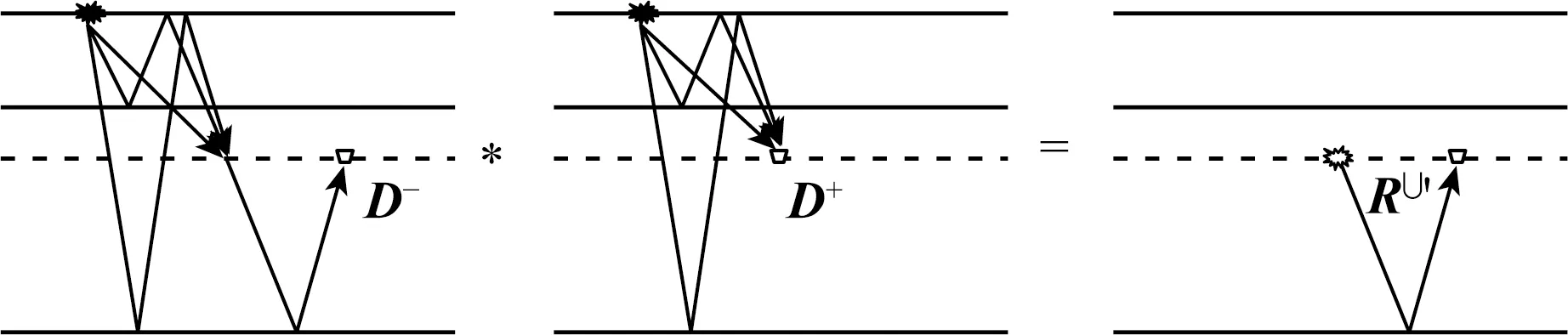
图5 多维互相关地震干涉基准面延拓示意图Fig.5 Schematic diagram of redatuming using multi-dimensional cross-correlation based on seismic interferometry
为了简洁且不失一般性,分析虚源法输出信号的具体成分时,暂时仅考虑图4和图5中三种有代表性的源端表面多次波路径.按方程(5)多维互相关得到的基准面延拓数据包含九种成分,即
(6)
为了便于理解,将它们以阵列形式展示.如图6,第一列表示基准面上的上行波信号,第一行表示基准面上的下行波信号的复共轭形式(频率域的复共轭在时间域相当于对称翻转,代表从零时刻起顺着波路经逆时或非因果传播),其余主体由3×3矩阵代表(6)式中的数据成分.当i=j时,由传播路径吻合的上、下行波互相关重构出有效信号,且主对角元素(即R∪′11、R∪′22和R∪′33)走时或相位一致,经同相叠加增强有效信号.当i≠j时,传播路径不吻合的上、下行波互相关形成串扰噪声.当地震记录含有不可忽视的高阶表面多次波时,上述阵列规模会变大,数据成分更多,其中包含阶次不对应、路径不吻合信号互相关形成的噪声.一般来讲,非对角元素的走时或相位差较大,干涉叠加后能量弱于有效信号.
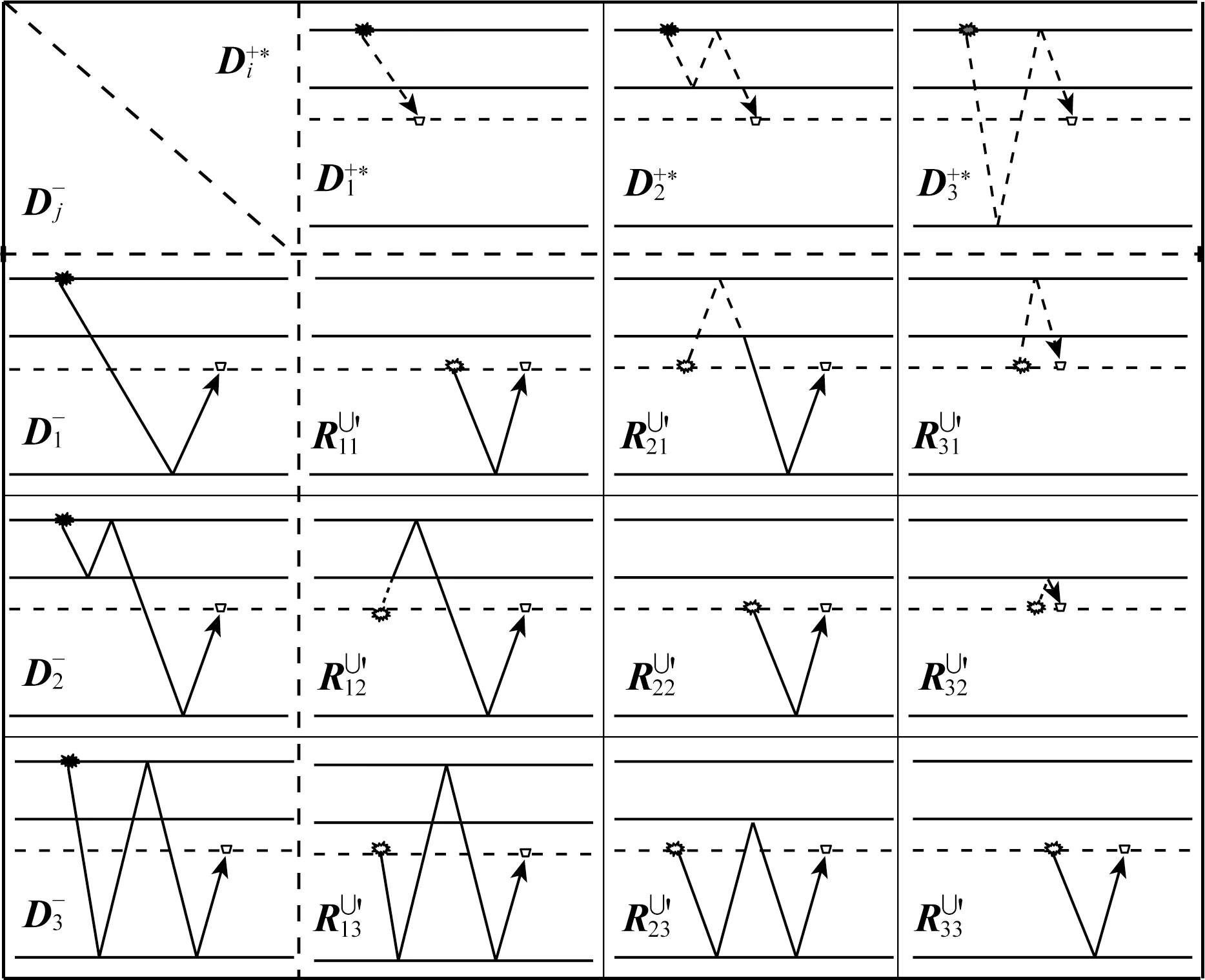
图6 基准面上-下行波记录的互相关实线代表正向传播,虚线代表逆时传播.Fig.6 Cross-correlation of up- and down-going seismograms at the datumSolid lines denote forward propagation and dashed lines denote reverse-time propagation.
由于自由表面影响以及实际的不完备观测,使得(5)式中的伴随算子与下行波逆算子差别较大,导致重构的波场信号包含较多无法干涉相消的串扰噪声.将(3)式代入(5)式,有
R∪′=HR∪.
(7)
对于完全弹性介质,地震波不发生频散,基准面延拓正、反问题均可按频率单独求解,故有
(8)
注意,等式两端虚拟观测数据检波器位置是对应的.方程(7)中H=D+*D+是基准面延拓问题对应的海森算子,可显式地写为:
(9)
它携带了观测系统尤其是实际震源的空间分布、时间函数及其带限特征,以及自由表面影响下的下行波传播(甚至散射)效应.也就是说,基于常规地震干涉原理的基准面延拓数据R∪′可以看作是预期的虚拟观测记录R∪经海森算子滤波(模糊化)的结果.
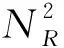
1.3 最小平方基准面延拓方法
理论上讲,对一次性基准面延拓获得的波场信号施加海森逆算子H-1,代表反模糊化滤波处理,进而重构高质量的虚拟观测信号,即:
R∪=H-1R∪′,
(10)
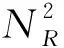
其中ε为正则化项的权重因子.如方程(2)和(7)所揭示的,在理想情况下虚拟观测信号不受震源时间函数或子波的影响,具有一定的稀疏特性,故采用L1范数正则化处理.于是,采用梯度类算法迭代估计虚拟观测信号:
(12)
其中k表示迭代次数,α表示步长,gk代表数据拟合项泛函梯度.注意,正则化处理采用了split Bregman方法(Osher et al.,2005; Yang et al.,2016).详细计算流程参见算法1.经过试算,本文数值算例中ε取值均为0.01.
参照附录B,以(2)式为状态方程,通过伴随状态法(Plessix,2006)可推导出泛函梯度的表达式:
(13)
它对应观测与正演信号拟合误差同下行波信号的多维互相关.第一次迭代的梯度计算与虚源法相当.综上所述,一旦从实际观测数据中分离出上、下行波信号,就可按这种数据驱动的最小平方基准面延拓(LSR)方法迭代更新基准面上的虚拟观测数据,其中自由表面和上覆介质的影响会在这个过程中逐步得到压制.
算法1: 稀疏约束最小平方基准面延拓
输入在基准面分离的下行波数据D+和上行波数据D-;
从k=0到最大迭代次数N循环以下计算
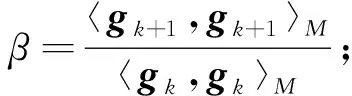
计算共轭梯度方向:zk+1=gk+1+βzk;
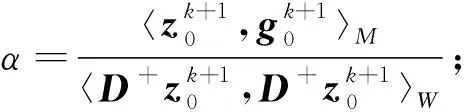
基准面数据更新:qk+1=qk-αzk+1;
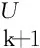
2 基于LSR压制海底地震数据表面多次波
海底观测地震信号可能受到海水层中的导波、海底界面波(Scholte波)以及涌浪等海洋噪声的干扰.通常会在前处理过程中滤除这些噪声.就针对反射纵波的数据处理而言,利用标定后的陆检垂直分量与声压分量的极性差异,借助PZ叠加或相减可从海底多分量记录中分离出上行波和下行波信号,从而压制检波器端表面多次波对上行波数据的影响(如Osen et al., 1999).利用分离出来的上、下行波信号,按前文LSR方法可消除地震波在海水层中的传播(与散射)效应以及海面相关的源端多次波效应.此时,基准面被选定为实施PZ叠加的海底界面.由于气枪震源一般位于海表以下,自由表面还会诱发源端的鬼波效应(图7a中以序号4标识).当地下介质存在火成岩、膏(盐)岩以及煤系夹层时,分离出来的下行波数据可能包含较强的层间多次散射/反射波.值得强调的是,本文这种数据驱动的LSR方法可以正确处理源端的鬼波以及层间多次波效应.重构的虚拟观测信号是源自于基准面之下的背向散射和反射波,其中一阶散射/反射波能量最强,是目标区域地震成像与速度建模最有用的信号.
3 数值实验
本文LSR通过数据驱动的迭代反演过程实现在基准面上的虚拟激发与接收,并剥离上覆介质和自由表面的影响.为了不失一般性,首先通过一个简单的层状模型演示LSR一次和多次迭代的处理效果,以及海森算子或PSF的作用.为了简化起见,先仅考虑图7中序号1、2、3标识的三种一阶表面多次波,接着再包含高阶表面多次波以验证它们在稀疏观测情况下对重构虚拟观测数据的重要贡献.然后通过一个横向变速模型合成OBC数据,展示LSR方法压制源端表面多次波(包括鬼波)的应用效果.为了便于控制多次波阶次并分析其影响,两个模型合成叠前炮记录均采用Berkhout(2014)提出的全波场正演方法,震源采用主频为20 Hz的Ricker子波.
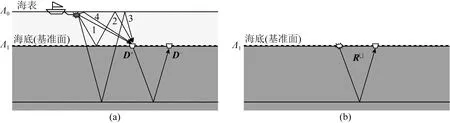
图7 海底地震数据基准面延拓示意图(a) 真实状态; (b) 理想状态.Fig.7 Schematic diagrams of redatuming for ocean bottom seismograms(a) Real state; (b) Ideal state.
3.1 层状模型
如图8,在三层模型的地表等间隔激发21炮,在深度500 m的水平井中均匀布设101个检波器,合成炮记录用于测试LSR算法.图9显示了在观测面分离出的上、下行波信号(暂时只包含一阶表面多次波).图10为经LSR重构的、虚拟震源位于基准面中央的反射信号.与图6呼应,在图10a显示的一次迭代获得的零炮检距地震道中,通过理论走时计算标识出了各个同相轴对应的波场成分,包括R∪′ii同相叠加构成的强振幅有效信号,以及其他非同相叠加产生的6个串扰噪声.因为干涉叠加后R∪′21走时趋近于零,波场向零炮检距聚焦,故其能量也较强(见图10a与图10b).随着迭代次数增加,串扰噪声逐渐减弱(图10c),残差快速下降并趋于稳定(图11).经过50次迭代,串扰噪声几乎被完全压制,重构反射波信号的垂向分辨率也有明显提高(见图10d).
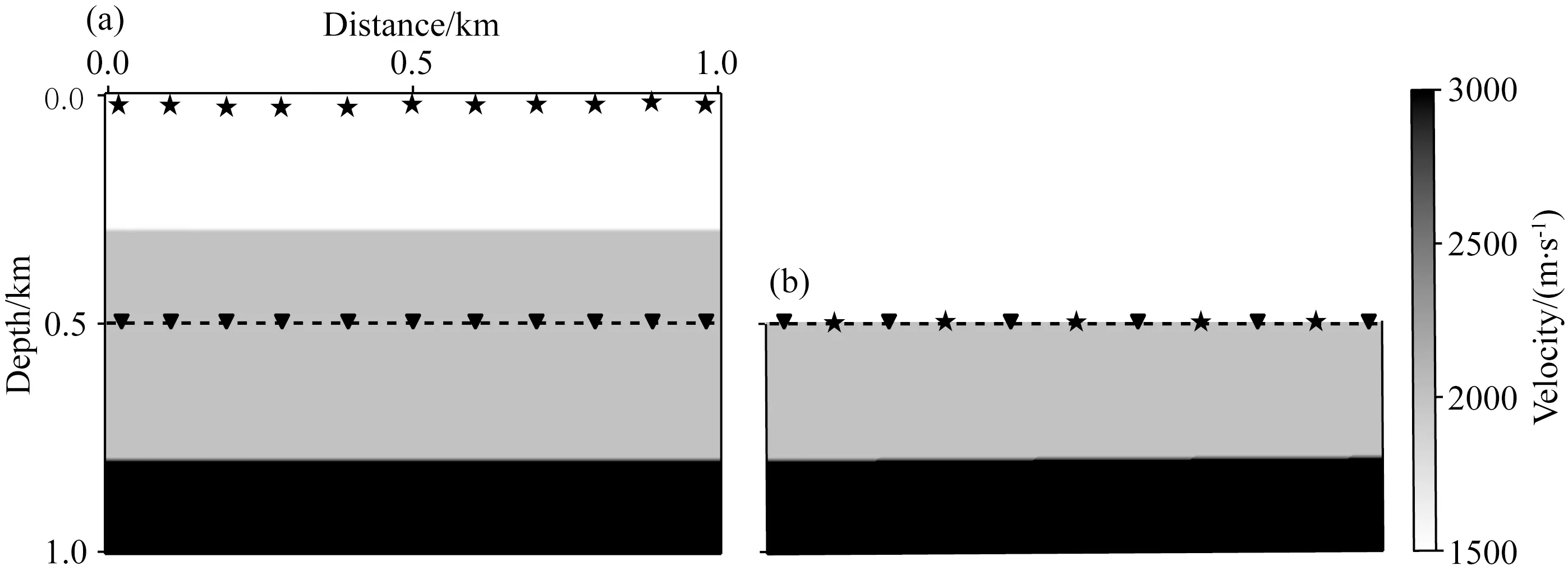
图8 层状模型(a) 真实状态; (b) 理想状态. 五角星表示震源位置,三角形表示检波器位置.Fig.8 A layered model for (a) real state and (b) ideal stateThe stars indicate the source location, and the triangles indicate the geophone location.
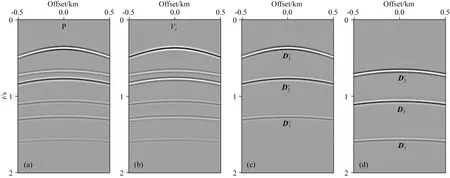
图9 基准面上的声压分量(a)和速度垂直分量(b)及分离的下行波(c)和上行波(d)记录Fig.9 Seismograms of (a) pressure and (b) vertical particle velocity,and the decomposed (c) up-going and (d) down-going signals at the datum
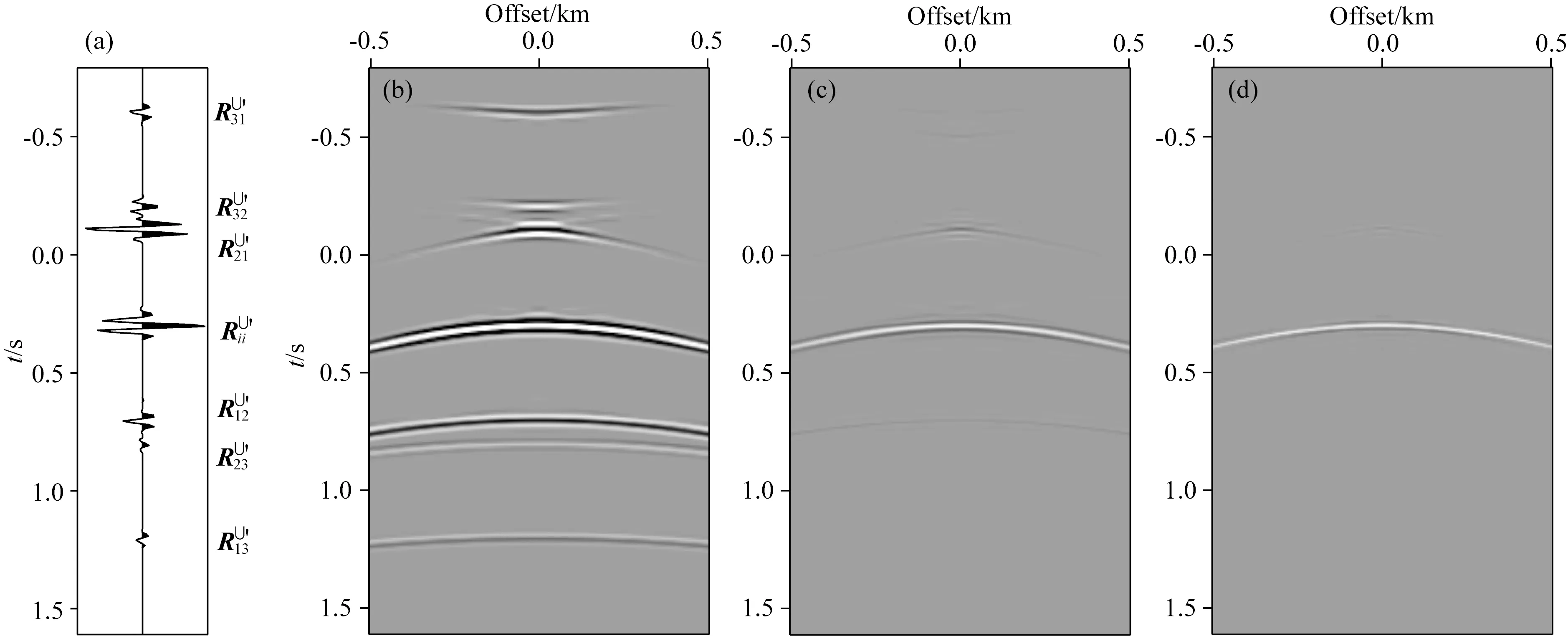
图10 最小平方基准面延拓实验(a) 第1次迭代后的零炮检距地震道; (b) 第1次、(c)第5次和(d)第50次迭代重构的单炮道集.Fig.10 Least-squares redatuming experiment(a) The retrieved zero-offset seismic trace of the first iteration; (b), (c) and (d) represent the retrieved common-shot gathers of the 1st , 5th and 50th iterations, respectively.
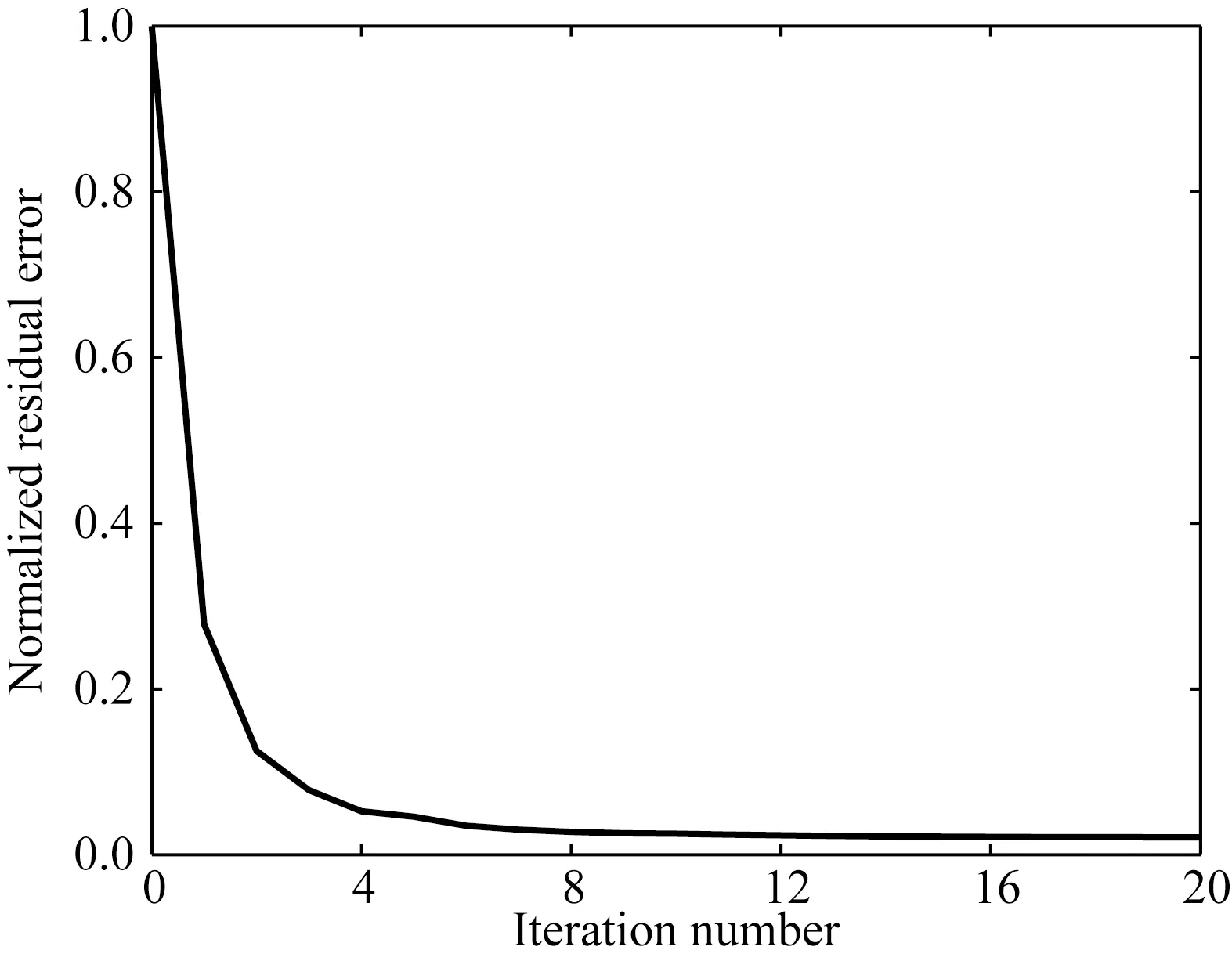
图11 层状模型实验残差收敛曲线Fig.11 Misfit curve of the experiment on the layered model
按前文分析可知,LSR一次迭代的结果可视为虚拟观测数据被海森算子模糊化滤波得到的,而且海森矩阵某一列与特定炮检对的PSF相对应.换个角度看,滤波后的点脉冲虚源被改造为以相应PSF为辐射模式的复合型虚源,从而在反射响应中耦合了自由表面、观测系统以及震源子波等效应.在本例中,下行波信号包含直达波和一阶自由表面多次波,沿物理波路径传播的上、下行波信号的互相关代表多次波向一次波的干涉转化和同相叠加,其他非对应路径上、下行波互相关产生无法干涉相消的串扰脚印.LSR迭代反演本质上相当于对图10b一次基准面延拓的炮记录施加图12中PSF的逆算子对应的滑动滤波(或虚源辐射模式矫正),通过去模糊化消除串扰噪声,重构基准面上虚拟激发与接收的高分辨率反射波信号.
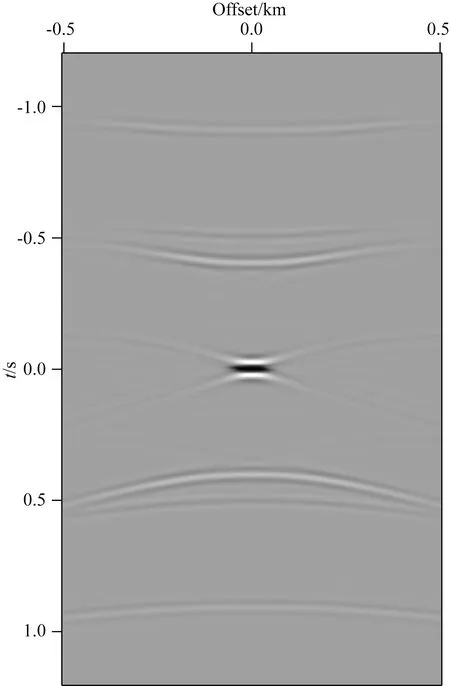
图12 在基准面中央激发和接收的虚拟炮检对所对应的点扩散函数Fig.12 A point spread function corresponds to a virtual survey of which both the source and receiver are in the mid of the datum
3.2 高阶表面多次波的贡献
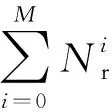
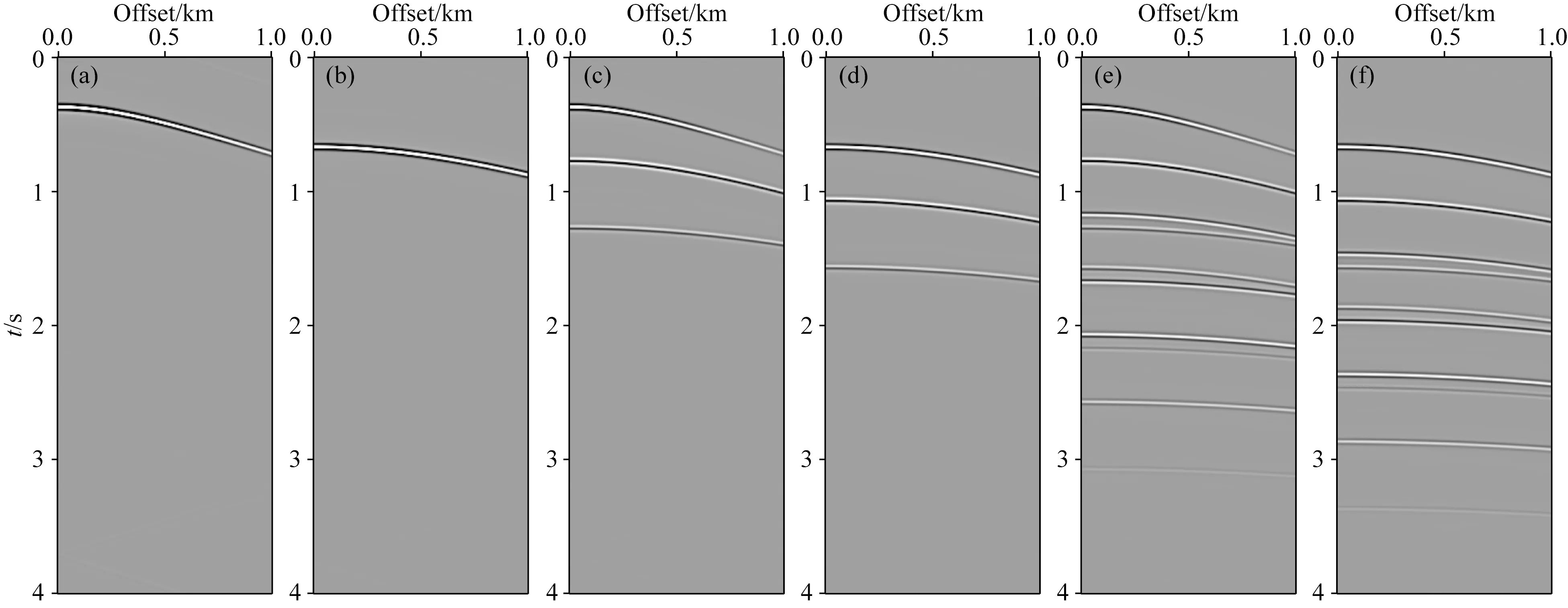
图13 某合成炮记录中分离的下行波与上行波信号(a,b) 不包含表面多次波; (c,d)含1阶表面多次波; (e,f)含1至3阶表面多次波.Fig.13 Separated down- and up-going waves of a synthetic common-shot gatherCommon-shot gather (a,b) without free-surface multiple, (c,d) with 1st-order free-surface multiples, and (e,f) with 1st to 3rd-order free-surface multiples.
为了揭示高阶表面多次波在干涉法基准面延拓中的贡献,下面在模型两端相隔1 km各激发一炮数据,通过LSR算法重构出虚拟震源等间隔分布在基准面的21炮叠前地震记录.图14显示了经50次迭代之后其中代表性的5炮道集.可见,由于高阶表面多次波参与基于干涉叠加的基准面延拓,模型中部弱照明问题得以明显缓解,预期的双曲型反射信号重构效果得到了明显改善(箭头指示).这表明一阶乃至高阶表面多次波提供的宽广照明对重构基准面之下的背向散射或反射波信号是非常有益的.否则,仅靠稀疏观测炮记录中的直达波和一次反射波信号,难以消除重构炮记录中目标反射同相轴在零炮检距附近的运动学误差(图中圈定区域),甚至在缺少实际震源的模型中央完全无法重构有效信号,出现较强的假信号.
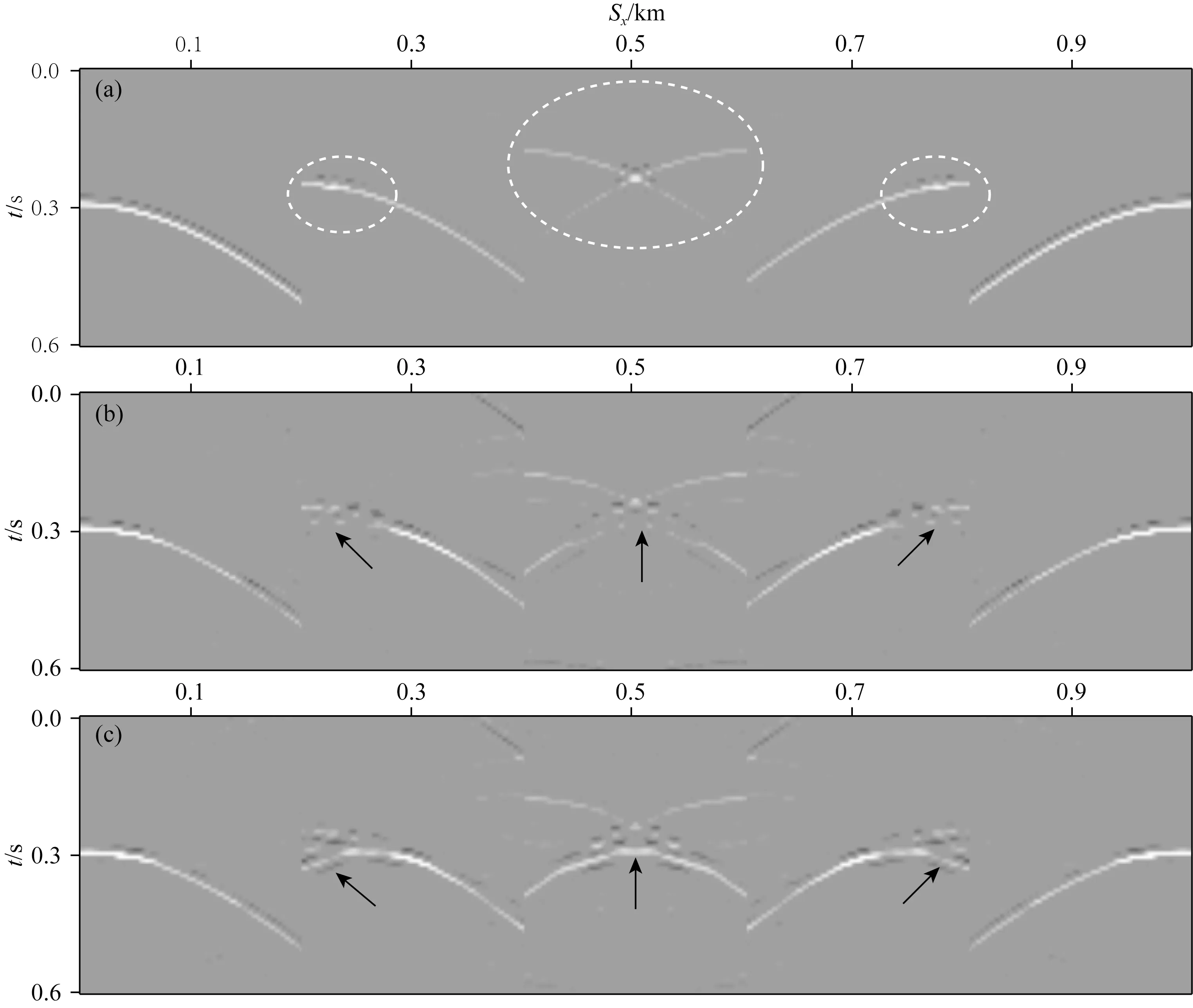
图14 含不同阶次表面多次波炮记录LSR输出的虚拟炮道集 (a) 原始炮记录仅含一次直达波和反射波; (b) 原始炮记录还包含1阶表面多次波; (c) 原始炮记录还包含1至3阶表面多次波.Fig.14 Reconstructed virtual common-shot recording by LSR with shot gathers having different order of free-surface multiplesTheoriginal shot gathers with (a) direct wave and primary reflection; (b) and with 1st-order free-surface multiples; (c) and with 1st- to 3rd -order free-surface multiples.
3.3 复杂模型OBC数据
接下来将LSR方法用于处理横向变速模型合成OBC数据,检验它能否压制海水层和自由表面对纵波信号的影响.在图15a展示的速度模型中,第一层是海水,第三、四层底界面存在较大起伏.假定由气枪震源从横向1~9 km范围内在海表以下10 m深处等间隔激发401炮,震源时间函数采用主频为20 Hz的Ricker子波.在海底横向2~8 km范围内均匀布设301个检波器,数值模拟401炮含有鬼波与多次波的原始OBC叠前道集.然后采用PZ叠加/相减,分离出上行波、下行波记录(如图16)用于后续LSR实验,拟重构基准面(海底)均匀分布151个虚拟震源在301个检波器接收到的背向散射与反射信号.
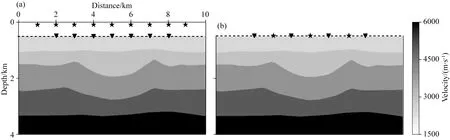
图15 速度模型与OBC观测系统(a) 真实状态; (b) 理想状态. (五角星代表震源,三角形代表检波器. Fig.15 Velocity model and OBC survey geometry for (a) real state and (b) ideal stateThe stars denote the sources and the triangles denote the receivers.
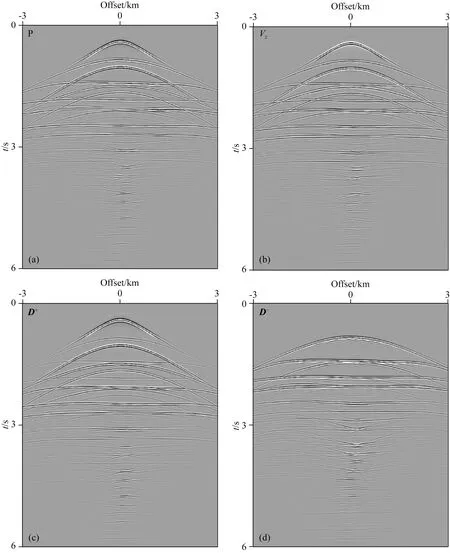
图16 实际震源位于横向坐标5 km处的OBC炮道集(a)原始声压场信号和(b)速度垂直分量,以及分离出的(c)下行波和(d)上行波信号.Fig.16 An OBC common-shot gather for a source at 5 km(a) Recorded pressure and (b) vertical particle velocity seismograms, and the decomposed (c) down-going and (d) up-going wavefield signals.
首先,按照海底的虚拟观测系统,采用Born模拟合成震源位于横向坐标5 km处一次反射波单炮记录(图17a),用于对比评估LSR处理结果.图17b和17c显示了LSR第1次和第50迭代输出的虚拟震源也在5 km处的单炮记录.而且,LSR最终输出的反射波波形更窄,频谱变得更宽(见图17c与18c).这是因为LSR既压制了鬼波与表面多次波造成的陷波效应(对比图18a与18c),又一定程度去除了子波效应,拓宽了信号频带,提高了时间分辨率(见图17c和图18c).可见,随着迭代次数增加,串扰噪声逐步得到压制,残差稳定减弱(图19),一次反射波信号得以有效重构.如图20,对比不同炮道集对应的叠前深度偏移结果,容易发现上-下行波分离消除了检波器端表面多次波对上行波数据成像的干扰(白色箭头),而多轮迭代LSR处理压制了源端表面多次波相关的假象(黑色箭头),基本消除了对反射界面成像的串扰,提高了成像剖面的分辨率和信噪比.
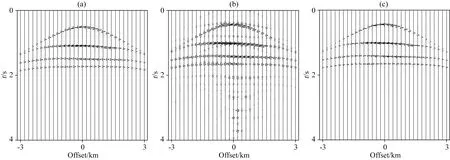
图17 基准面重构数据(a) Born正演参考数据; (b) 一次迭代重构数据; (c) 50次迭代重构数据.Fig.17 Datum reconstructed data(a) Reference data from Born forward modeling; (b) Direct redatuming data and (c) LSR data obtained with Fig.15a as input.
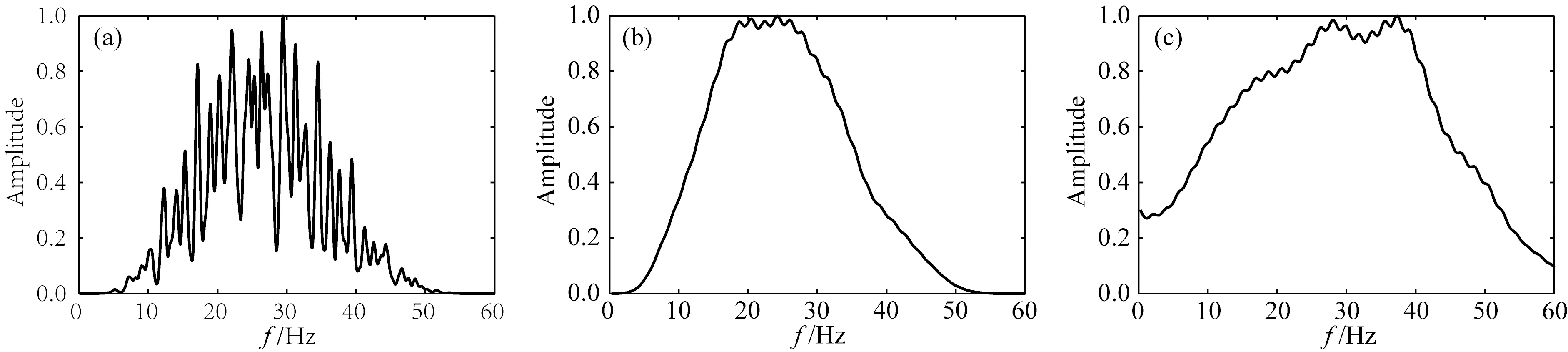
图18 原始与重构炮道集单道频谱对比(a) 原始上行波信号(与图16d对应); (b) Born模拟反射波(与图17a对应); (c) LSR重构反射波记录(对应图17c).Fig.18 Comparison of the spectra for the up-going wave in the original and the retrieved common-shot gathers(a) Original upgoing waves (corresponding to Fig.16d); (b) Primary reflection synthesized by Born modelling (corresponding to Fig.17a); (c) Retrieved signal by LSR (corresponding to Fig.17c).
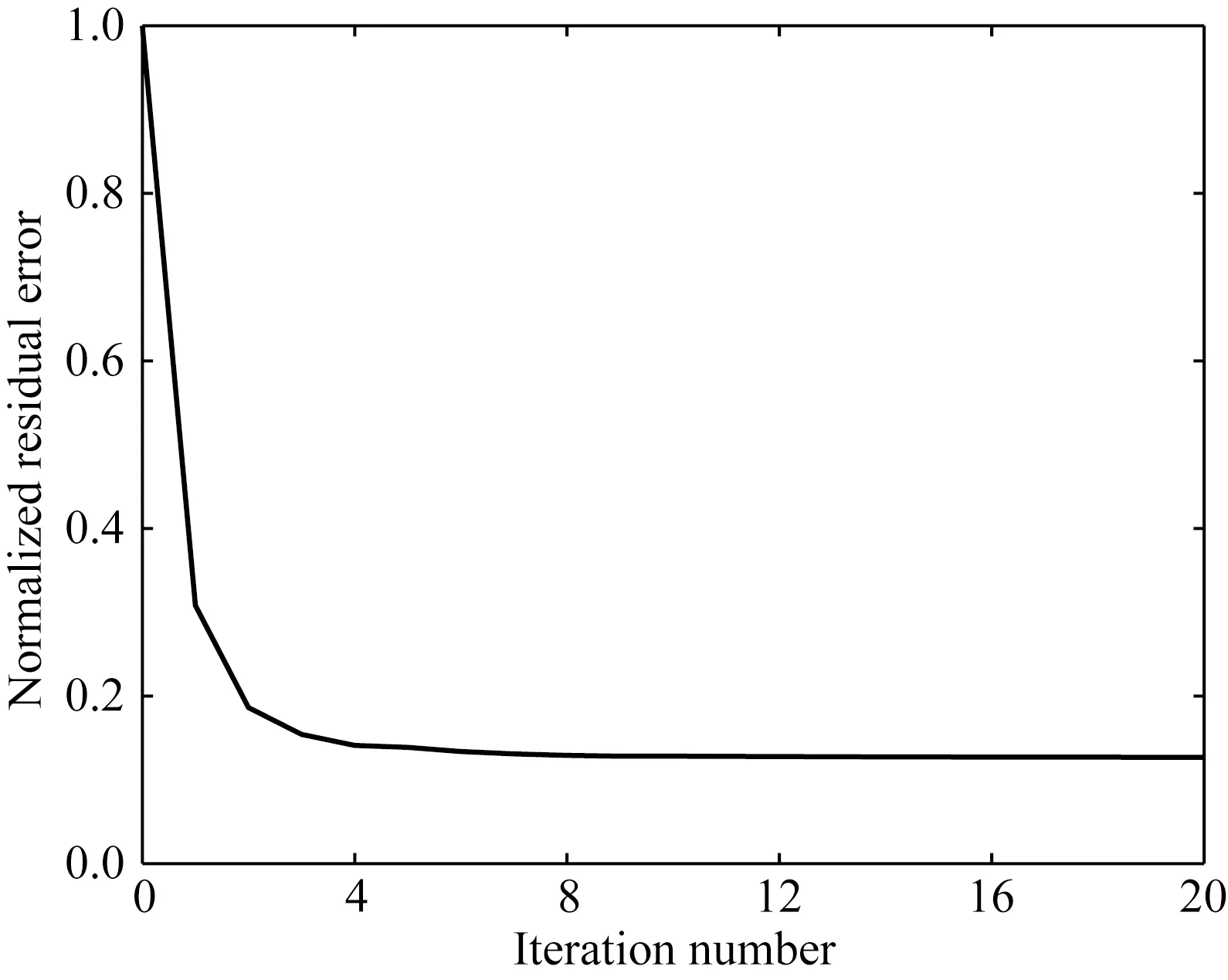
图19 复杂模型实验的残差收敛曲线Fig.19 Misfit curve of the experiment on the complex model
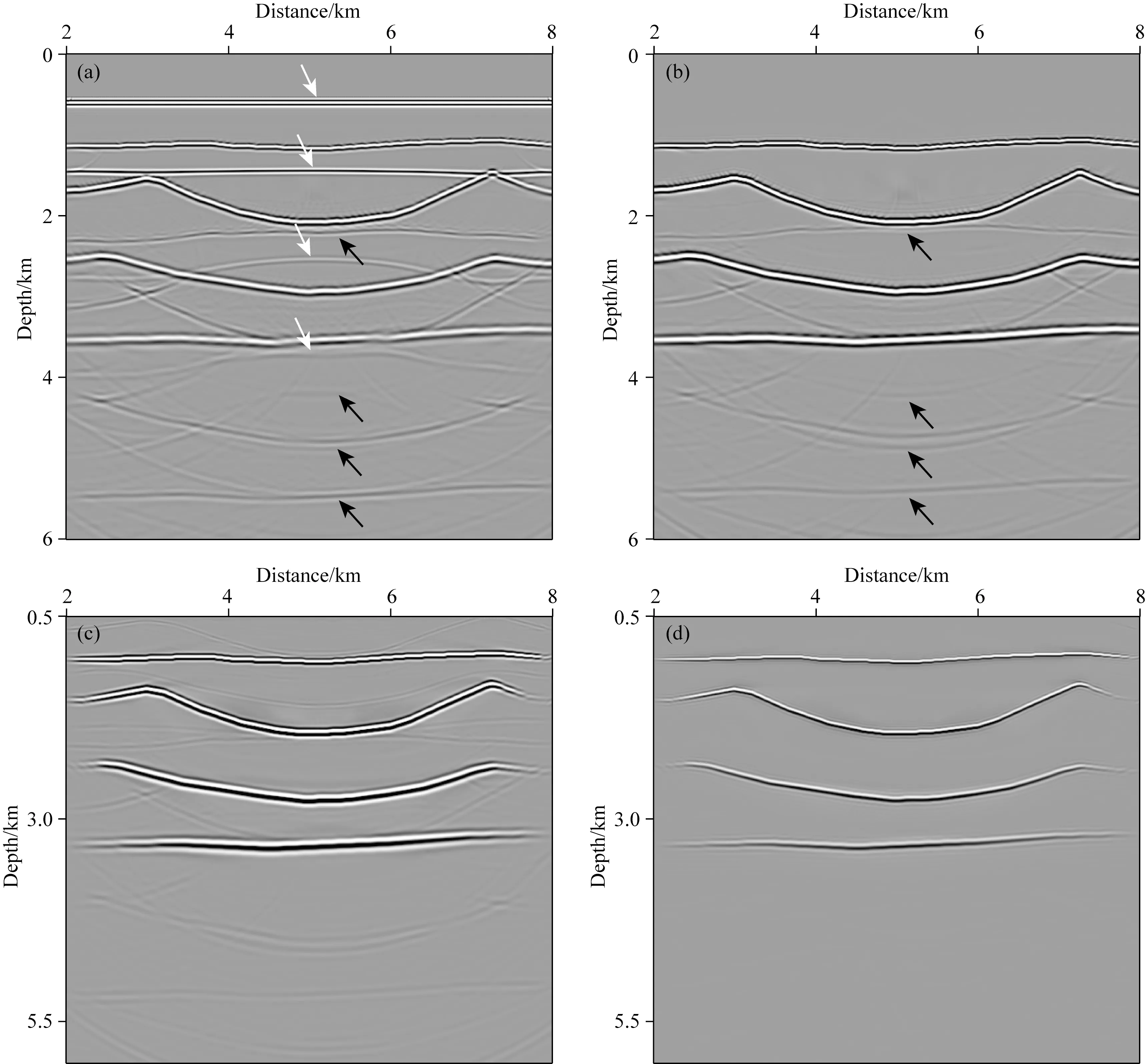
图20 输入不同炮道集的叠前深度偏移结果(a) 原始炮道集; (b) 分离后的上行波道集; (c) 经1次LSR迭代重构的虚拟炮道集; (d) 经50次LSR迭代重构的虚拟炮道集.Fig.20 Comparison of prestack depth migration results for various common-shot gathers(a) Input original gathers without up/down separation; (b) Input up-going waver field signal; Input reconstructed common-shot gathers after the (c) 1st and (d) 50th iteration of LSR.
4 讨论
针对OBN/OBC数据处理是一个复杂的系统工程,多次波压制需要一些必要的、合理的前处理步骤进行支撑.在完成检波器方向与耦合校正以及水检-陆检标定之后,联合声压与垂直速度分量的PZ叠加/相减分离出上、下行纵波信号,这就基本消除检波器端表面多次波对上行纵波记录的干扰.在此基础上,本文LSR方法通过多次迭代,干涉转化或消去的是源端表面多次波.如果数据中存在较强的横波能量,需要在海底观测面采用弹性波场分离方法(Muijs et al., 2004;刘学义等,2021a),则可在分离上-下行波之后进一步实现纵波与横波信号的模式解耦.理论上讲,以分离的上、下行P/S波作为输入,采用本文方法能够重构出已克服自由表面和海水层影响的PP和PS虚拟反射数据.这将在今后研究中加以验证.
值得注意的是,对大多数OBN/OBC数据来说,震源分布较为稠密,满足干涉法对空间采样的要求(即不存在图13那种极端稀疏观测情况).与OBC采集方式不同,由于OBN节点或者海底地震仪(OBS)造价比较昂贵,检波器分布相对稀疏一些.虽然LSR方法比较准确地重构出了任意两个检波器之间的格林函数场,形成海底虚拟观测记录,但若检波器间隔太大,会给后续偏移成像或参数反演带来挑战.对于海洋拖缆采集方式,若采用传统的单分量声压检波器,从观测记录分离上、下行波比较困难.若采用水-陆双检(dual sensor)观测方式,则可用PZ叠加/相减分离上、下行纵波信号.本文姊妹篇将讨论如何利用LSR原理消除拖缆地震数据中的表面多次波.
本文LSR方法完全是数据驱动的,与地下速度模型无关,因此直接适用于各向异性、黏滞性介质.它涉及的正演和泛函梯度计算分别通过上-下行波多维褶积和多维互相关实现.在CPU型号为Intel Xeon E7-8890的多核工作站上,前文二维简单模型和复杂模型的每一炮单次迭代平均耗时分别为1.2 s和18.4 s,总的计算量不大,但虚拟观测数据需要较大的内存开销,拓展到三维情况要从计算策略上加以优化.对深水或深层目标勘探而言,经LSR输出的虚拟观测数据已经剥离了自由表面和上覆介质的影响,显著压缩了模型空间和数据规模,有利于开展面向局部目标的精细反演成像,预期也可在油藏开发或二氧化碳填埋的时移地震监测中发挥积极作用.
5 结论
一次基准面延拓利用多维互相关消除上、下行波场中共同的波路经,从而在一定程度上剥离自由表面和上覆海水对基准面重构数据的影响,但仍然会产生能量较强的、由非匹配路径波场信号互相关引起的串扰噪声.借助最小二乘优化反演思想,本文LSR方法不仅能够很好地消除这些串扰噪音,还可一定程度压制不完备观测、鬼波效应和子波带限效应的影响,提升虚拟观测信号的分辨率和频带宽度.该方法充分利用表面多次波的照明优势和最小平方反演迭代过程,无需对表面多次波进行比较困难的分离或分阶提取即可实现向一次波的干涉转化.数值实验表明重构数据基本消除表面多次波的干扰,改善后续基于一阶散射理论的叠前偏移成像效果.
致谢感谢王腾飞老师、邹鹏博士、武泗海博士和黄河硕士等在本文研究过程中提供的建议.
附录A:基于互易定理构建实际观测和虚拟观测波场状态之间的转化关系
欲利用模型无关的基准面延拓方法克服表面多次波的影响,需建立实际观测和理想状态(无自由表面效应)虚拟观测之间波场信号的转化关系.这里采用的理论工具是由亥姆霍兹方程和高斯定理推导的单向波互易定理(Wapenaar et al. 2004).它揭示了封闭无源区域两个相互独立状态下波场的卷积或相关沿着封闭边界的积分是守恒的.卷积型互易定理用于描述波场传播问题,而相关型互易定理主要用于波场反向延拓、逆时聚焦以及干涉成像等(Schuster,2009;Wapenaar,2004).下面利用卷积型互易定理建立从虚拟观测数据到实际观测数据的映射(正演)方程.
根据文献(de Hoop,1988;Fokkema and van den Berg,1993),假定存在两个相互独立的波场状态A和B,它们在两个水平无限延伸界面Λi和Λj包围的封闭区域内介质特性保持一致且没有震源(封闭区域外介质特性可能不同,且可能存在震源),则单向波卷积型互易定理在频率-空间域具有如下形式(Wapenaar,1996;Wapenaar et al.,2004):
(A1)
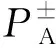
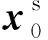
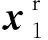
令Λi=Λ1,Λj=Λ2,将上、下行波格林函数场代入公式(A1)表征的褶积型互易定理,有:
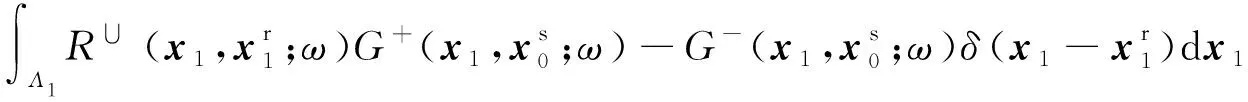
(A2)
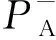
(A3)
它在时间域对应的多维褶积给出了地表脉冲震源激发、基准面检波器实际记录的上行波G-同在基准面虚拟激发、接收的上行波R∪之间的关系.
附录B:基于伴随状态法推导LSR泛函梯度
(B1)
针对LSR采用的L2范数目标泛函,形成如下约束优化问题:
=0.
(B2)
通过拉格朗日乘子法,将其转化为非约束优化问题,即:
(B3)
其中R表示取实部操作,λ为伴随状态变量.由于F(R∪,D-)=0,故有J(R∪)=L(R∪,D-,λ).
方程(B2)对应的最小化问题等价于寻求增广泛函L(R∪,D-,λ)的鞍点,对应其一阶偏导数为0的解,即:
(B4)
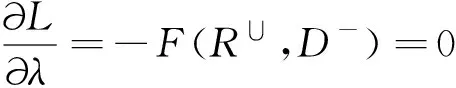

(B5)
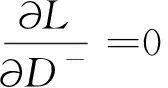
(B6)
其中δD-表示模拟数据与观测数据的残差.
由于λ与R∪无关,故有
(B7)
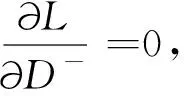
(B8)

