二维与三维大地电磁反演的敏感度研究

孟绿汀， 张慧茜， 黄清华*

1 北京大学地球与空间科学学院地球物理系， 北京 100871 2 河北红山巨厚沉积与地震灾害国家野外科学观测站(北京大学)， 北京 100871

0 引言

大地电磁法以天然交变电磁场为场源，通过在地表观测电场强度和磁场强度来研究地球内部电性结构.由于其对低阻层的高敏感度以及深达软流圈的探测深度，大地电磁法被广泛应用于资源勘探(Queralt et al., 2007)、岩石圈结构探测(Zhang et al., 2016)、地震孕震环境研究(叶涛等，2021)等方面.该方法假设电磁波以平面波形式透射入地表，利用电磁波的探测深度随频率变化的特征来重构地下结构的电阻率模型(陈乐寿和王光鄂，1990).由于大地电磁反演为非线性反演且耗时较长， 大多数实际研究仅关注反演给出的物理参数模型并结合地质资料对其进行解释，易于忽视反演模型的可靠性与分辨率等信息.事实上由于反演问题的多解性，反演模型可能与真实地质结构存在一定差异.此外，由于电磁扩散场的物理本质，大地电磁法重建的深部电性结构往往还具有分辨率不足的问题.定量估计大地电磁反演模型的可靠性和分辨率，能为后续精细地质解释提供依据.因此，如何构建经济高效、易于实现的反演结果评价方法，成为受到广泛关注的问题.

反演模型的可靠性可以从多种角度评价，评价方法各有优劣.采用解析方法计算趋肤深度(陈小斌等, 2007, 2019; Borah and Patro, 2019)和最大探测深度(Spies, 1989; Huang, 2005; 肖调杰等, 2015)简便易行，但只适用于一维层状模型，难以扩展到二维、三维场景.三维反演通常因为模型参数过多导致分辨率矩阵、协方差矩阵难以直接计算与存储(Menke, 2015)，因此衍生了许多间接计算的方法.非线性敏感度测试(Dong et al., 2014; Zhang et al., 2016)、探测深度指数(Oldenburg and Li, 1999; Oldenborger et al., 2007; Carrière et al., 2017)和目标函数极值分析(Jackson, 1976; Meju, 2009; Kalscheuer et al., 2010; de Wit et al., 2012)等间接方法常被应用于评价电磁反演结果.此类方法需要额外设计模型或重新求解最优化问题，所以很少应用于三维场景.基于高斯过程(Astic et al., 2020; Olierook et al., 2021) 或贝叶斯反演(Minsley, 2011; Xiang et al., 2018; 周思杰和黄清华, 2018; Ray and Myer, 2019; Manassero et al., 2020; Seillé and Visser, 2020; Blatter et al., 2021; Peng et al., 2021)等概率类反演方法可同时获得解的分布与不确定性.尽管可以采取高维奇异值分解、主成分分析等方法(Tompkins et al., 2011; Tompkins, 2012; Fernández-Martínez, 2015; Fernández-Martínez et al., 2019; Grana et al., 2019)对模型参数和数据参数进行降维处理，但耗时的正演计算和低效的采样算法依旧限制概率类方法与自抽样方法(Schnaidt and Heinson, 2015)在三维场景的应用.

随着算法的完善与计算力的提升，三维大地电磁反演技术已成为主流，但受限于野外工作环境、施工成本等因素，往往无法得到阵列式分布的大地电磁台站，台阵分布为多条长剖面相互交叉，这种情况下二维反演技术依然具有重要的应用价值 (Habibian Dehkordi et al., 2019; Nagarjuna et al., 2021).前人通过对三维数据进行二维反演揭示了二维反演潜在的局限性(Ledo et al., 2002; Ledo, 2006)，同时也利用三维反演解释二维剖面数据(Siripunvaraporn et al., 2005; 林昌洪等, 2011).尽管三维解释技术具有一定的优越性，但如何针对实际情况对比和分析二维与三维反演模型的差异依然具有较强的研究意义.本文尝试发展一种基于敏感度矩阵的反演模型评价方法，该方法的运算规模较小，且能够定性分析二维与三维反演结果的可信度.此外，大地电磁阻抗张量的对角元素、非对角元素与倾子在反演中对模型重建具有不同的贡献(Kiyan et al., 2014)，不同分量在数据采集中的信噪比及反演设定的误差限也存在一定差异，从理论上探讨各阻抗分量的敏感度对于实测资料解释具有一定指导意义.本文从求解三维大地电磁正演模型的伴随问题来获取完整的敏感度矩阵，并基于敏感度矩阵定量分析大地电磁数据不同阻抗分量敏感度，形成了一套经济高效的反演结果评估方法.该方法能够获得异常体的边界、垂向分辨率等信息.研究还利用合成数据定量讨论非阵列式数据二维与三维反演的有效探测深度，为二维反演与三维反演结果的对比提供了理论依据.

1 敏感度矩阵计算方法

如式(1)所示，敏感度矩阵表征数据对模型变化的响应，能够展示数据对模型的约束能力：

(1)

其中m为模型参数，f(m)为模型到数据的映射函数.

本文基于三维交错网格有限差分法(Egbert and Kelbert, 2012) 求解正演问题的伴随问题，间接得到完整敏感度矩阵计算公式.离散形式的频率域电磁偏微分方程一般表示为式(2)：

Sme=b,

(2)

其中b向量为边界条件与场源项，Sm为稀疏系数矩阵，e为交错网格中主网格上的电场值.由于磁场分量可由电场的旋度给出，此种情况下计算阻抗张量的函数与模型参数无直接关系，大地电磁正演过程可用式(3)描述：

f(m)=d(e(m)),

(3)

其中d为从离散电场值到阻抗张量、倾子的映射函数.对式(3)关于m求偏导可得敏感度矩阵：

(4)

将式(4)写作矩阵形式(5)：

J=LF,

(5)

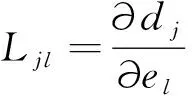
Sm0F=P,

(6)

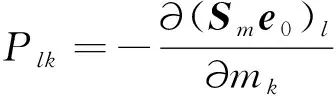
(7)

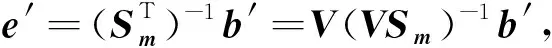
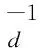
(8)

其中diag为提取矩阵对角线元素，Wd为数据协方差矩阵，表示对敏感度矩阵做关于数据误差的归一化，E为Nd×Nd(数据个数)的对角系数矩阵.E的对角线元素取值区间为0到1，取值代表该数据分量对模型影响的权重.当E为单位矩阵时，表示所有数据对模型参数影响的总和.通过至多Nd次计算可得到完整敏感度矩阵.

2 模拟结果

2.1 合成模型

合成数据测试使用的模型如图1所示，在100 Ωm的均匀半空间内交错排列有6个1000 Ωm的高阻异常(蓝色)和6个10 Ωm的低阻异常(红色)，厚度分别为10 km、25 km、60 km，中心深度12.5 km、32 km、92.5 km.模型网格划分为60×60×60个，中心计算区域网格为40×40×60个，水平网格尺寸5 km×5 km，边界区域由10个以1.5倍递增的网格组成，纵向网格第一层为20 m，以1.2倍向下递增.

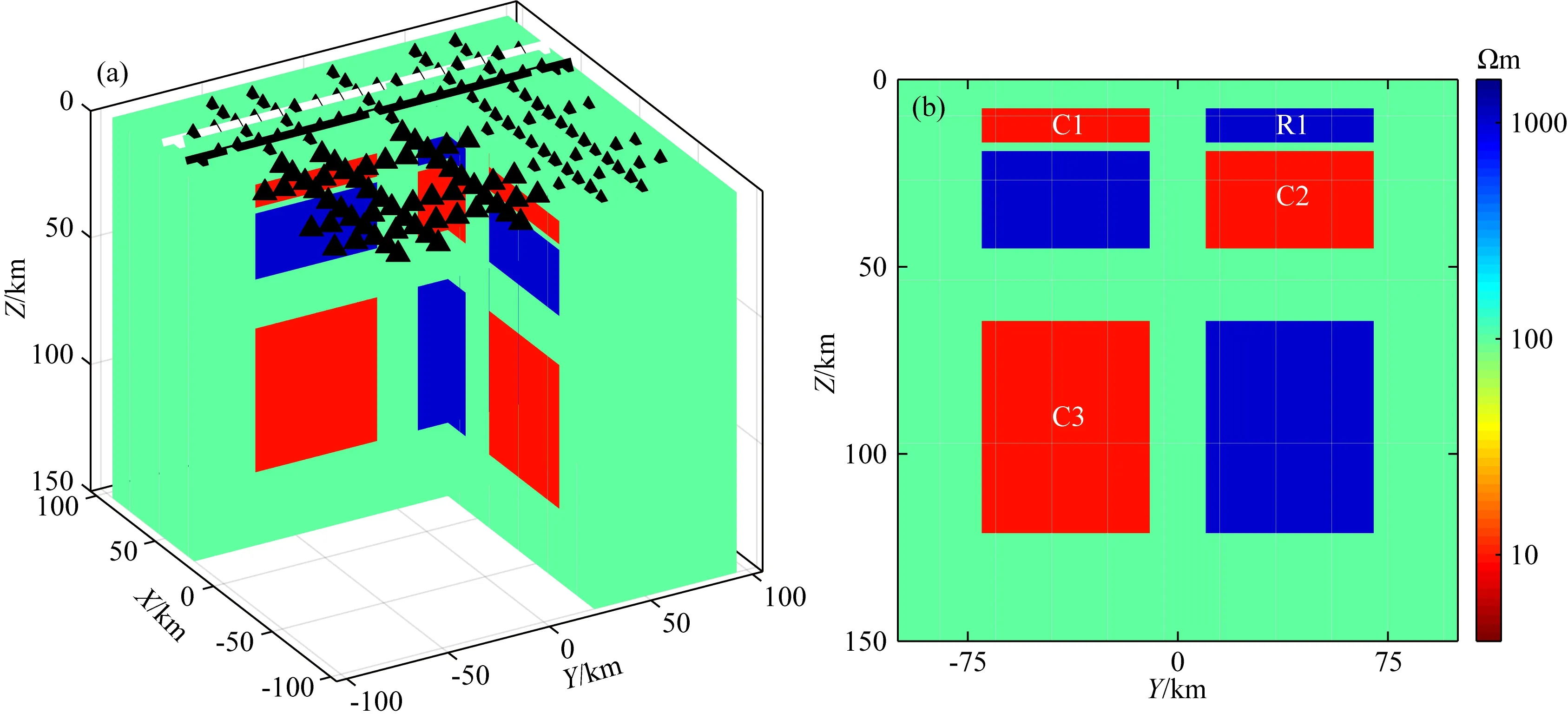
图1 (a)合成模型示意图蓝色为1000 Ωm 高阻异常体，红色为10 Ωm 低阻异常体.黑色实线(X=40 km)和白色实线(X=60 km)为本文研究涉及的垂向切片的位置，黑色三角表示数据接收点，白色三角表示模型中心处数据接收点.(b)沿黑色实线的垂向切片，其中C1、C2和C3表示低阻异常体，R1表示高阻异常体.Fig.1 (a) Synthetic model composed of anomaliesBlue and red colors indicate 1000 Ωm high and 10 Ωm low electrical resistivity anomalies, respectively. The solid black line (X=40 km) and solid white line (X=60 km) indicate the location of the vertical slices in this study. The black triangles indicate the stations and the white triangles indicates the locations of the station in model center. (b) The vertical slice along the solid black line where C1—C3 represent the three conductive anomalies and R1 represents the resistivity anomalies.

2.2 不同分量的敏感度

使用2.1节的合成模型，计算所有台站阻抗张量非对角元素、阻抗张量对角元素和倾子矢量的敏感度矩阵，周期范围0.2～8000 s，等对数间隔频点25个点.图2为部分代表性周期下阻抗张量非对角元素Zxy+Zyx的敏感度.在短周期时，高敏感度分布于浅层，集中在测点附近，这是因为大地电磁法满足扩散方程，短周期对应的趋肤深度较小.长周期时模型深部敏感度增加，不同周期下敏感度峰值处于不同的深度，与大地电磁反演常规认识一致.随着周期增加，灵敏度高的主要分布区间的厚度增大，一方面是因为模型网格尺寸随深度递增，导致灵敏度高的主要分布区间增厚.另一方面即使使用等间距网格，也会存在逐渐增厚的高灵敏度主要分布区间.表明大地电磁法对深部结构的分辨率有限.非对角元素的敏感度主要分布在横向边界附近，且低阻异常体附近的敏感度较大.

图2 不同周期下所有台站Zxy+Zyx敏感度沿X=40 km的垂向切片黑色虚线指示异常体位置.Fig.2 Vertical slices of all stations Zxy+Zyx sensitivity along X=40 km at different periodsThe dashed black lines indicate the locations of the anomalies.

如图3所示，阻抗张量对角元素不仅在低阻异常体附近有高敏感度，在高阻异常体边界处也有高敏感度，可以重建异常体边界.图4中倾子矢量的敏感度集中于异常体边界处，在异常体内部很小.值得注意的是，阻抗张量非对角元素的敏感度大于阻抗张量对角元素和倾子矢量的敏感度，表明权重相同时，非对角元素多用于重建研究区域内大尺寸结构，而对角元素和倾子矢量对部分边界敏感度高，在重建异常体的边界等精细结构上具有一定贡献.

图3 不同周期下所有台站Zxx+Zyy敏感度沿X=40 km的垂向切片黑色虚线指示异常体位置.Fig.3 Vertical slices of all stations Zxx+Zyy sensitivity along X=40 km at different periodsThe dashed black lines indicate the locations of the anomalies.

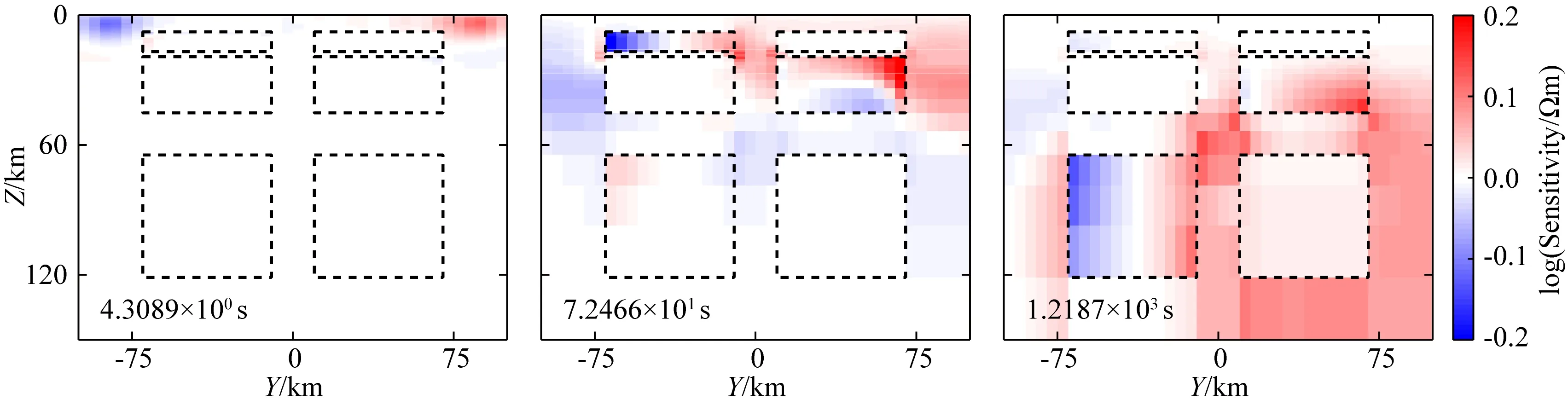
图4 不同周期下所有台站Tx+Ty敏感度沿X=40 km的垂向切片黑色虚线指示异常体位置.Fig.4 Vertical slices of all stations Tx+Ty sensitivity along X=40 km at different periodsThe dashed black lines indicate the locations of the anomalies.

图5为模型中心位置数据接收点(图1中白色三角)位置的全分量敏感度，虽然该点远离异常体正上方，但同样对异常体有敏感度.由于该点位于合成模型的中心对称点，敏感度在浅部横向对称分布，图6的深度5 km的横向切片显示敏感度呈现中心对称的十字型，周期4.3 s处敏感度达到峰值，表明在5 km处该周期起主导作用.

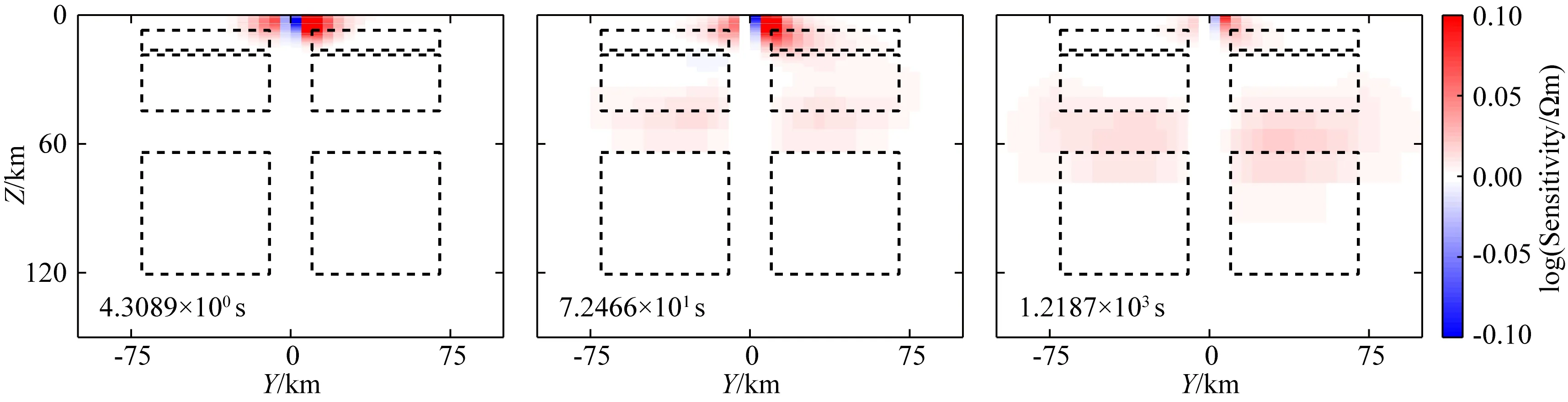
图5 不同周期下模型中心点位置全分量敏感度沿X=40 km的垂向切片黑色虚线指示异常体位置.Fig.5 Vertical slices of full component sensitivity of the model midpoint along X=40 km at different periodsThe dashed black lines indicate the locations of the anomalies.

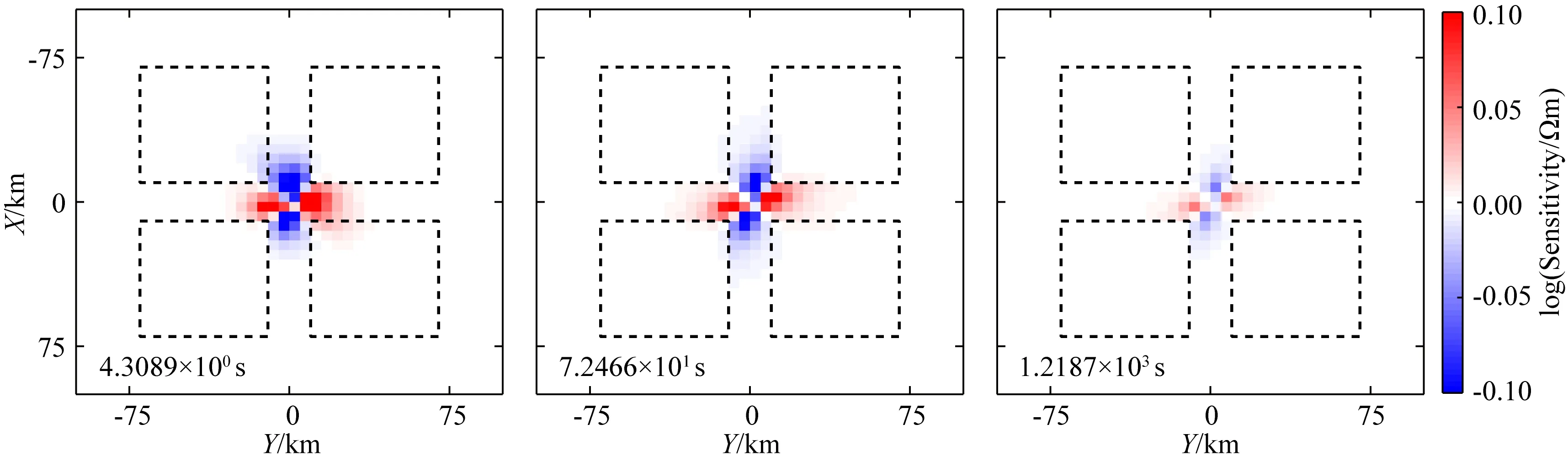
图6 不同周期下模型中心点位置全分量敏感度在深度5 km的水平切片黑色虚线指示异常体位置.Fig.6 Horizontal slices of full component sensitivity of the model midpoint along Z=5 km at different periodsThe dashed black lines indicate the locations of the anomalies.

3 二维与三维反演的对比

本文介绍的敏感度矩阵计算方法同样适用于二维反演，通过计算二维大地电磁反演中的敏感度矩阵，定量对比理论二维、三维反演的敏感度.研究选用图1中平行于YOZ平面的黑色实线剖面计算二维敏感度，周期范围为0.2～8000 s，等对数间隔频点25个.二维反演通常使用TM模式(蔡军涛和陈小斌, 2010)，当剖面平行于YOZ平面时，二维TM模式对应三维YX模式，三维Zyx分量和二维TM分量具有一定的可比性.将剖面上所有网格求和并除以敏感度矩阵最大值归一化，如图7所示，虽然随着周期增加，两种反演的敏感度均有所下降，但二维反演敏感度始终高于三维反演，且在长周期部分差距更为明显.需要指出的是，真实的地下结构往往具有一定三维性，实测数据可能不满足二维构造假设.为更好地指导实际应用，有必要对比三维合成数据的二维与三维反演结果，并探究反演模型中异常体边界的划定方法.

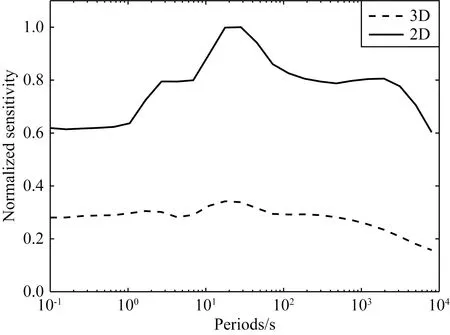
图7 二维与三维下反演归一化敏感度对比Fig.7 Comparison of normalized sensitivity in two-dimensional and three-dimensional inversions

3.1 异常体边界的划定

二维与三维反演使用第2节中加入误差的三维合成数据，其中倾子给定0.02的绝对误差，阻抗张量主对角元素给定10%的相对误差，非对角元素给定5%的相对误差.三维反演使用全阻抗张量和倾子矢量，二维反演使用TM分量.反演的初始模型为100 Ωm均匀半空间，初始正则化因子100，二维和三维反演结果的均方根数据拟合误差均收敛到1.05.本文选择了两条分别代表弱三维性(图1黑实线)和强三维性(图1白实线)剖面来进行二维与三维反演结果的对比.

由于体积效应的存在，大地电磁反演结果中，异常体与背景构造之间存在电阻率值过渡带.如图8所示，统计三维反演中三个低阻异常体C1—C3及其过渡带的电阻率分布，直方图显示电阻率分布存在峰值，在超过95%分位数时，电阻率值出现频次迅速降低，表明该阈值可以视为异常体边界.二维反演结果的边界重建方法相同，选取95%分位数作为阈值.多次的合成数据测试显示，95%分位数的阈值虽然是人为给定的数值，但具有一定的通用性.异常体中心测线的二维与三维反演结果如图9所示，黑色虚线指示异常体的真实位置，黑色菱形为重建异常体内部的极值，表示异常体的中心位置.三维反演和二维反演对浅部低阻异常体C1和C2的重建结果相似，三维反演得到的边界与真实边界更吻合.对于深部低阻异常体C3，三维反演敏感度在该深度范围较小，难以恢复异常体电阻率值，但使用全阻抗张量进行反演，重建的异常体边界与真实边界较为一致.虽然三维反演比二维反演更加吻合真实边界，但三维反演得到的异常体中心位置偏浅，二维反演得到的异常体中心更接近真实位置，并且在此深度范围内依然有较大敏感度，能够有效恢复电阻率值.图10为远离异常体中心测线的二维和三维反演，结果显示三维反演依然能够重建异常体边界，强三维性导致二维反演无法重建异常体，“拖尾”现象严重，出现虚假高阻异常.

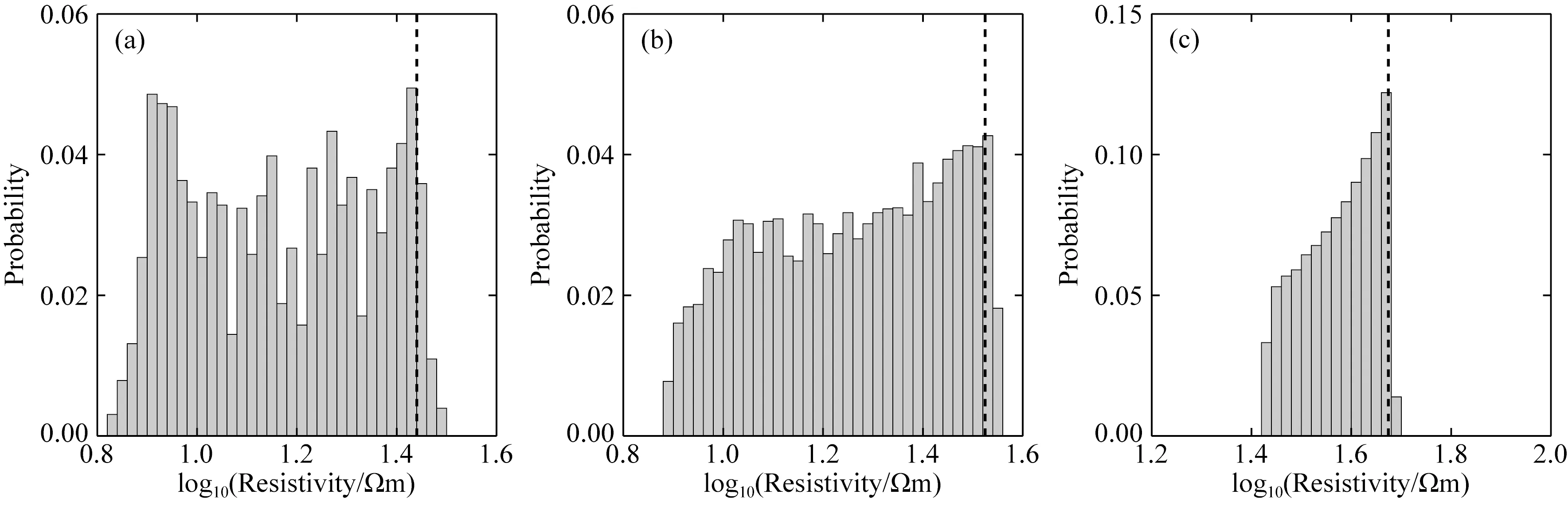
图8 三维反演中异常体(a) C1, (b) C2和(c) C3及其过渡带的电阻率分布黑色虚线指示95%分位数的电阻率值.Fig.8 Electrical resistivity distribution of anomalies (a) C1, (b) C2 and (c) C3 and their transition zones in the three-dimensional inversionThe electrical resistivity values at the black dashed line are at 95% quantile.

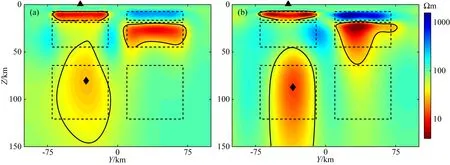
图9 合成数据(a)三维、(b)二维反演的电阻率模型垂直切片(X=40 km)黑色虚线指示异常体真实位置.黑色实线指示重建的异常体边界.黑色三角为计算垂向分辨率矩阵的位置.黑色菱形指示重建的异常体中心.Fig.9 Vertical slices of synthetic data (a) three-dimensional inversion and (b) two-dimensional inversion electrical resistivity model along X=40 kmThe dashed black lines indicate the true locations of the anomalies. The solid black lines indicate the reconstruction boundary of anomalies. The black triangles show the location of vertical resolution matrix. The black diamonds indicate the reconstruction center of anomalies.

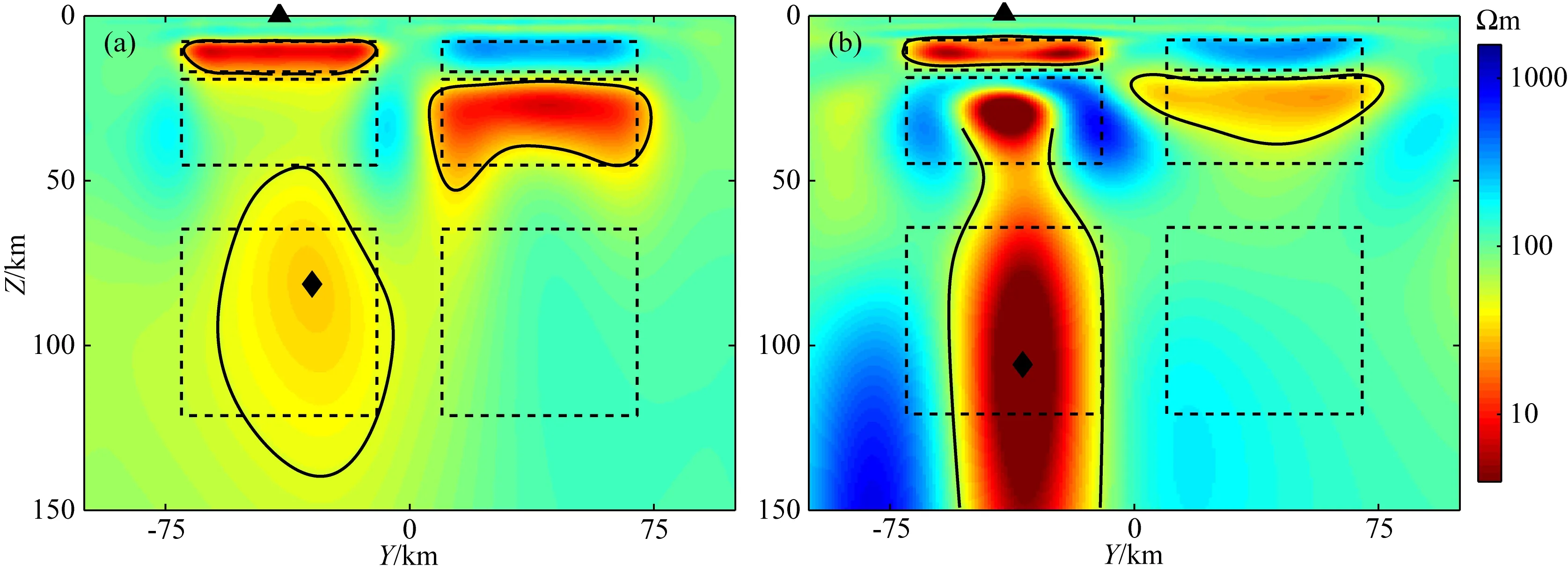
图10 合成数据(a)三维、(b)二维反演的电阻率模型垂直切片(X=60 km)黑色虚线指示异常体真实位置.黑色实线指示重建的异常体边界.黑色三角为计算垂向分辨率矩阵的位置.黑色菱形形指示重建的异常体中心.Fig.10 Vertical slices of synthetic data (a) three-dimensional inversion and (b) two-dimensional inversion electrical resistivity model along X=60 kmThe dashed black lines indicate the true locations of the anomalies. The solid black lines indicate the reconstruction boundary of anomalies. The black triangles show the location of vertical resolution matrix. The black diamonds indicate the reconstruction center of anomalies.

3.2 模型垂向分辨率

根据完整的敏感度矩阵，仿照线性反演中模型分辨率矩阵的定义式(9)(Egbert and Booker, 1992)计算了反演结果中不同位置的模型垂向分辨率其中P为二阶正则化矩阵，λ为最终反演结果对应的正则化因子.本文中垂向网格划分为60个，频点25个，阻抗张量和倾子矢量共6分量，考虑所有测点的影响总和，实际计算时只截取三维模型中的垂向一列，得到150×60的敏感度矩阵.理想状态下的模型垂向分辨率矩阵应该为一单位矩阵.如图11a所示，三维反演在(X=40 km,Y=-40 km)处分辨率极值主要集中于对角线两侧，等值线随深度增加逐渐扩散，表明反演结果是真实模型均匀平滑后的结果.图11b中二维反演的分辨率等值线在深度20～50 km向上偏离对角线，100 km后向下弯曲偏离对角线，说明二维反演结果在20～50 km深度上可能偏向于深部结构，在100 km深度以下偏向于浅于100 km的真实结构(即C3).图11c和图11d分别为三维、二维反演结果位于(X=60 km,Y=-40 km)处的垂向分辨率矩阵，由于该测点下方结构的三维性更强，二维反演分辨率等值线偏离对角线程度更大.对比结果显示当结构具有强三维性时，二维反演的垂向分辨率较差.

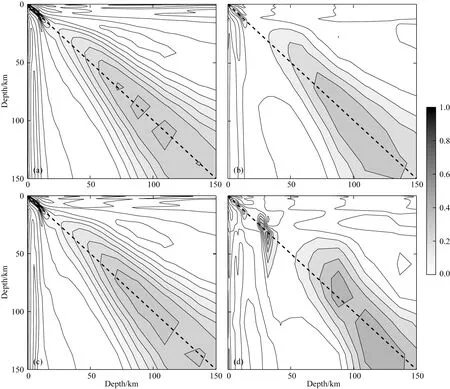
图11 (a)三维反演和(b)二维反演位于(X=40 km, Y=-40 km)处的垂向分辨率矩阵.(c)三维反演和(d)二维反演位于(X=60 km, Y=-40 km)处的垂向分辨率矩阵黑色虚线指示分辨率矩阵的对角线.Fig.11 Vertical resolution matrix at the location of (X=40 km, Y=-40 km) for (a) three-dimensional inversion and (b) two-dimensional inversion. Vertical resolution matrix at the location of (X=60 km, Y=-40 km) for (c) three-dimensional inversion and (d) two-dimensional inversionThe dashed black line indicates the diagonal line of the resolution matrix.

R=P-1JT(JP-1JT+λI)-1J,

(9)

4 结论

本文采用求解大地电磁正演伴随问题的方法，计算各个频点、观测分量和数据接收点在模型上的响应，得到了完整敏感度矩阵.敏感度矩阵对网格大小、数据接收点位置和目标函数的变化等均有响应，因此分析完整敏感度矩阵，有助于优化反演网格划分、野外测点布设和反演参数选择.本文在敏感度矩阵基础上计算模型垂向分辨率，并结合反演结果的电阻率分布，提出了一种定量表征异常体边界的方法.二维与三维反演合成模型测试表明，三维反演对浅部低阻异常体的重建优于二维反演.当电性结构三维性不强时，二维反演在深部具有更高敏感度，可以有效恢复深部低阻异常体的电阻率值，为深部地质解释提供定量约束.三维反演虽然能有效重建异常体边界，但无法恢复深部低阻异常体的电阻率值，并且重建的异常体中心偏浅.当电性结构三维性较强，三维反演重建的边界与真实位置更加吻合.二维反演所出现的“拖尾”现象并非对应真实结构，虚假异常体会对精细地质解释产生阻碍.因此针对由多条长测线交叉组成的非阵列式数据，建议在三维性不强的研究区域，联合使用二维和三维反演技术，提高深部地质解释的可靠性和准确性.