大落差输油管道局部高点水击压力预测方程研究*

孙璐璐，李长俊，贾文龙，张财功，余秋爽，罗金华

(西南石油大学 石油与天然气工程学院，四川 成都 610500)

0 引言

大落差输油管道所处地形复杂，局部落差大，压力差值高达4～8 MPa[1]。因此，管道在停泵、关阀作业中，极易出现水击问题，水击发生时，减压波[2]使得流过的管段压力降低，当压力低至油品饱和蒸气压时，会引起油品中轻质组分气化，产生的气泡运移、聚集在管道局部高点处，严重时引发液柱分离现象，造成管道失稳变形，危害管道正常运行[3-6]。由于大落差管道起伏较大，管道局部高点处的稳态运行压力较低，当瞬变流动工况发生时，局部高点压力会在压力波作用下进一步降低。因此，准确预测大落差管道局部高点瞬变压力，对于及时防止管道高点气泡聚集，保障大落差输油管道安全运行意义重大。

目前，国内外学者对输油管道动态水击问题开展研究：李伟等[7]分析输量变化与阀门动作对海底注水管道水击压力的影响；肖学等[8]采用拉丁超立方抽样法对长距管道工程事故停泵时管道瞬变流动水击计算模型进行全局敏感性分析，发现敏感度较高的参数为管径、关阀时间及管道输量。近年来，数值模拟技术的发展为水击分析提供技术上的突破[9-12]。Tae-oh等[13]采用CFD方法分析水击引起的管内压力状况及其变化；陆赛华等[14]采用SPS软件研究不同水力瞬变工况下长输管道内压力、流量波动情况；Ammar等[15]采用WaterGEMS并结合HAMMERCFD计算程序模拟分析管道水力瞬态过程。

现有研究主要基于传统水击计算方法[16]，采用管道末端阀门关闭模型对水击问题展开研究，针对大落差输油管道系统不同位置处阀门动作产生的水击影响进行评价比较困难。同时，大落差输油管道较平坦地区管道的水击波传播及压力波动情况存在显著差异，且水击过程复杂、影响因素众多。目前，围绕大落差输油管道的水击问题进行高点压力预测及变化规律的研究较少，现有研究方法难以准确预测大落差输油管道局部高点的压力变化机理。

鉴于此，本文针对大落差输油管道局部高点的压力预测问题，建立输油管道动态水击计算模型，考虑实际工况中水击发生位置存在多种可能性，并结合国内某大落差原油管道实际参数进行不同条件下关阀水击模拟，分析大落差输油管道动态水击规律。采用通用全局优化算法(Universal Global Optimization,UGO)与列文伯格-马夸尔特法(Levenberg-Marquardt, LM)，建立大落差管道局部高点压力预测方程，并对方程进行验证。研究结果可为大落差输油管道的安全运行与管理提供参考。

1 数学模型

1.1 水击基本方程

输油管道水击数学模型由连续性方程与运动方程构成，如式(1)～(2)所示：

(1)

(2)

式中：H为压头，m(油柱)；v为介质在管轴x处的流速，m/s；cf为压力波波速，m/s；α为管道倾角，rad；g为重力加速度，9.8 m/s2；x为管轴坐标，m；t为时间，s；D为内直径，m；A为管道截面面积，m2；λ为管壁与油品间的摩阻系数；Q为流量，m3/s。

1.2 水击波速计算

管道中的水击波动可视为声波运动[17]。在无限大流体中声波运动传播速度基础上，考虑管壁弹性与液体可压缩性[18]，推导水击波速如式(3)所示：

(3)

式中：E为管材弹性模量，Pa；δ为壁厚，m；ρf为管输油品密度，kg/m3；Kf为油品的体积弹性系数，Pa。

1.3 水击压力计算

根据动量定理分析水击发生后产生的水击压力，如式(4)所示：

(4)

式中：ΔH为水击增压，m(油柱)；v为液体流速，m/s。

2 数值模拟

2.1 模型建立

基于OLGA管流瞬态模拟软件，结合中缅大落差原油管道基础参数建立水击仿真模型如图1所示。管输介质为沙特轻质原油，密度为856 kg/m3。

图1 管道仿真模型

中缅原油管道存在多处大落差段，考虑怒江跨越处与澜沧江跨越处最大，落差分别为1 480，1 200 m[19]，同时管道沿线存在2处翻越点(1#翻越点169.4 km，2#翻越点473.7 km)，因此选取包含该范围的3处管段作为研究对象，局部高点及选取管段位置如图2所示。局部高点位置可根据高点距离上游站场的管线长度L1确定，动作阀门的位置由阀门与高点之间的高程差h及管线长度L2共同确定。通过利用模型进行不同条件下的关阀水击模拟，分析局部高点水击波变化规律。

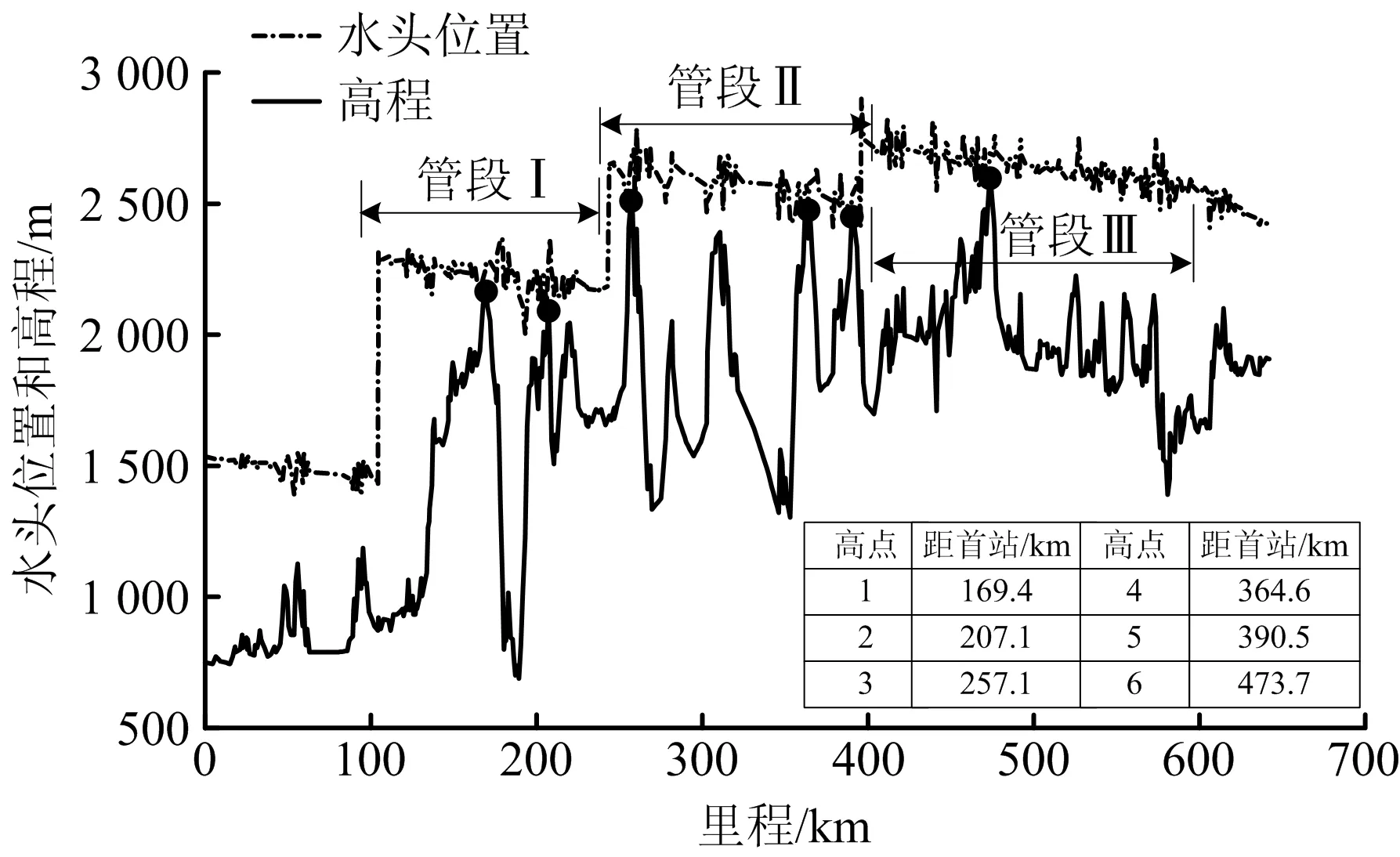
图2 局部高点及选取管段的位置情况

管道实际运行输量范围为1 000×104～1 300×104t/a。根据SCADA系统反馈数据，将各管段在不同输量条件下的稳态运行压力与OLGA软件模拟的稳态运行结果进行对比，见表1。由表1可知，误差范围在0.17%～1.86%，验证模型的可靠性。

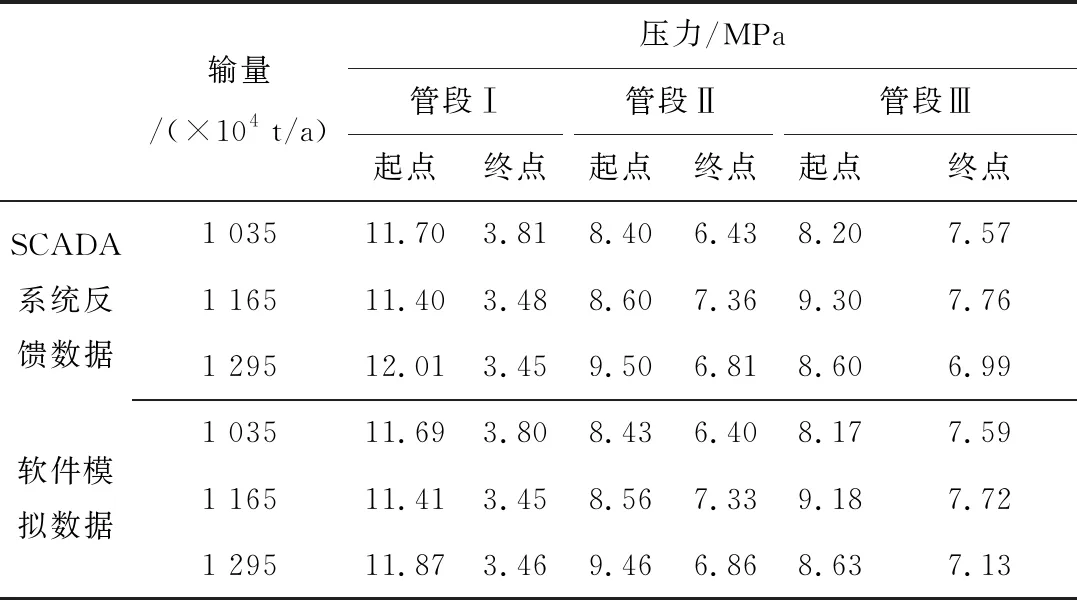
表1 选取管段的稳态运行压力情况

2.2 模拟工况设计

考虑大落差输油管道中影响高点水击压力的参数包括介质流速v，关阀时间t，局部高点稳态初始压力P0以及动作阀门位置(由h与L22个参数共同确定)。基于表1，确定模型介质流速为0.78，0.87，0.96 m/s。工况条件见表2，进行不同关阀时间(t=60，120，180 s)的水击模拟，得到局部高点稳态压力低于0.6 MPa时，不稳定流动工况中高点会出现不同程度低压。

3 主要因素分析

由表2可知，对高点水击压力影响程度较大的参数为介质流速v，关阀时间t，高点初始稳态压力P0以及管线长度L2。选取落差最大的管段Ⅰ，研究不同条件下关阀水击模拟中1#翻越点即高点1的压力变化，分析各参数对高点水击压力值的影响。

表2 模拟工况

3.1 高点初始稳态压力P0

当v=0.78 m/s，阀门位置L2=15.8 km，关闭时间t=180 s时，不同初始稳态压力P0下的关阀水击压力对比如图3所示。由图3可知，初始稳态压力P0越小，在同样水击增压情况下局部高点压力越小，高点处油品更容易发生气化，进一步佐证保障高点稳态压力可避免不稳定流动中出现液柱分离现象。

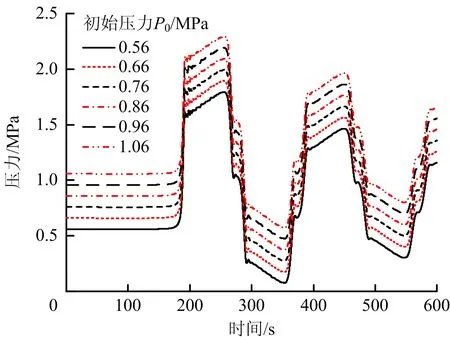
图3 不同初始压力P0下的水击压力对比

3.2 管内介质流速v

阀门位置确定即L2=15.8 km，阀门关闭时间t=180 s时，不同输量下的关阀水击压力对比如图4所示。由图4可知，当初始稳态压力确定，管内介质流速越大，水击产生的增压越大，阀门关闭产生的水击压力波动越剧烈，从而导致管道局部高点处更容易形成低压。

图4 不同介质流速下的水击压力

3.3 关阀时间t

当v=0.78 m/s，P0=0.37 MPa，L2=15.8 km时，关阀时间不同的水击压力对比如图5所示，关阀时间越短，水击波形振荡越剧烈，高点处的低压持续时间越长；当关阀时间大于120 s时，会在一定程度上减少高点低压持续时间。

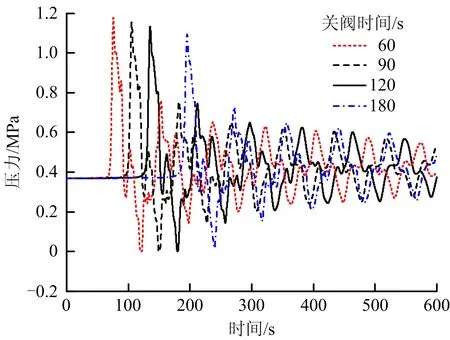
图5 不同关阀时间下的水击压力

3.4 动作阀门与高点之间距离L2

当v=0.78 m/s，P0=0.61 MPa，t=180 s时，动作阀门位置不同时的水击压力对比如图6所示，关阀位置距离高点越远，压力波在传递过程中的衰减程度越大，即水击波传递到局部高点处产生的瞬变压力下降，则高点处越不易形成低压状态。

图6 动作阀门与高点之间不同距离时的水击压力

4 局部高点压力预测方程建立

在实际工程中，一般根据局部高点处的压力值与油品的饱和蒸气压对比判断该处油品是否发生气化。其中，油品饱和蒸气压力主要基于原油气液相变转换模型[20]计算。当局部高点处的压力低于油品的气化压力，油品中轻质组分挥发，若低压持续时间较长，将会导致气泡大量聚集，影响管道安全运行。局部高点在不稳定流动工况下的压力可通过压力预测方程计算实现。

4.1 预测方程的建立

大落差输油管道高点处水击压力变化是多因素相互影响、共同作用的结果。基于1stOpt 软件，考虑对局部高点水击压力影响显著的介质流速v，关阀时间t，高点初始稳态压力P0，管线长度L2，结合阀门与高点之间的高程差h、局部高点距上游管线长度L1，采用LM法与UGO算法相结合的方法，建立局部高点水击压力预测方程如式(5)所示：

P=f(v,t,h,P0,L1,L2)

(5)

方程拟合建立过程中，为减少变量个数，令tanα=h/L2，其中α为管道与水平面的夹角。同时，为准确得到各参数与局部高点压力间的关系，采用分步方式进行拟合，具体步骤为基于表2计算不同模拟条件下的tanα值，根据模拟结果选取任意2个影响参数值与高点压力模拟值进行拟合，选取产生方程式中相关系数R较大的2组，分别为0.976，0.634。如式(6)～(7)所示：

(6)

Y2=b1×v2+b2×v+b3+exp(-1)L1

(7)

将式(6)～(7)中的计算值分别与剩余参数值进行拟合，取相关系数大的方程如式(8)所示：

Y3=c1+c2×Y1+c3×Y12+c4×Y13+c5×t

(8)

拟合相关系数R为0.975。

将式(7)～(8)的计算值与高点压力模拟值进行拟合得到式(9)：

(9)

整理代入即得到局部高点压力P与h，L2，P0，t，v，L1之间的关系，如式(10)所示：

(10)

拟合相关系数R为0.987。

式中：Ci=n2×ci；Yi为函数符号；P为高点压力，MPa；v为管内介质流速，m/s；t为关阀时间，s；P0为高点稳态压力，MPa；L1为局部高点距上游的管线长度，km；L2为局部高点距动作阀门的管线长度，km；h为局部高点与动作阀门的高程差，m；ai，bi，ci，ni为拟合常参数。常参数值见表3。

表3 常参数值

结合管道实时监测系统数据，采用局部高点压力预测方程计算局部高点压力值，并与油品的饱和蒸气压力比较。

4.2 方程评价与误差分析

为验证预测方程的准确性与适用性，分别以管段Ⅰ，Ⅱ，Ⅲ为对象，设定异于拟合方程的工况。运用OLGA软件模拟关阀水击，并与预测方程计算得到的高点水击压力值进行比较，结果见表4，管段Ⅰ，Ⅱ，Ⅲ的相对误差分别为1.58%，3.93%，3.43%，均小于5%，表明本文预测方程能较好的分析发生水击时局部高点的压力变化情况。

表4 验证结果

5 结论

1)在大落差管道关阀水击瞬变过程中，影响管道局部高点水击压力的关键参数为介质流速v、高点初始压力P0、动作阀门距高点距离L2及关阀时间t。

2)高点初始稳态压力越小，发生水击时油品越容易气化；管内介质流速越大或阀门位置距离高点越近，局部高点处越容易形成低压；关阀时间越短，局部高点处的低压持续时间越长。关阀时间大于120 s时，高点低压持续时间减少。

3)以管段Ⅰ，Ⅱ，Ⅲ为对象，验证本文预测方程，得到计算相对误差分别为1.58%，3.93%，3.43%，均小于5%，表明所建立的方程能够较好地预测局部高点水击压力。