高浓度全尾砂充填料浆流变特性及管路输送沿程阻力损失研究
梁新民,王怀勇,江国建,陈小伟,谢盛青(.中国恩菲工程技术有限公司,北京 00038;.招金矿业股份有限公司,山东 招远 65400)
1 前言
自工业革命以来随着矿产资源的大规模开采,赋存在地表浅部的高品位富矿资源已接近枯竭,矿山开采活动已经转入到深部开采,深井开采带来高岩温热、高地应力、高裂隙水压以及岩爆等一系列程地质灾害。与此同时,矿产资源的大规模开采导致地下产生大量采空区,造成地表塌陷、水资源流失等问题;地表堆存矿山固废的排土场和尾矿库占用大量土地,严重威胁了生态环境的可持续发展[1]。高浓度全尾砂充填采矿技术作为一种安全高效的绿色技术,在确保深井开采安全的情况下兼具生态环境保护和改善矿石贫化、损失率的多重功效,近年来得到相关行政部门和矿山企业的大力推广应用。
矿山充填系统设计时,需要对充填料浆的流变特性进行试验研究和定量分析,建立正确的流变模型。目前国内外不少专家、学者已经对高浓度尾砂充填料浆的流变特性和阻力损失计算进行了大量的研究,并基于重力理论和能量理论总结出沿程阻力的计算方法,如卡杜里斯基公式、杜兰德公式、金川公式、鞍山黑色金属矿山公式、会泽公式等,这些公式是在特定实验下得到的,受到设备、成本和现场条件等多方面条件的限制,存在针对性强、可复制性差等缺点,主要适合于自由沉降强的非均质流料浆[2]。高浓度全尾砂充填料浆属于非牛顿流体,即所谓的结构流体,只有正确的建立流变模型才能描述充填料浆的流变特性。随着计算机技术的不断成熟和更新,利用数值仿真软件模拟非牛顿流体的管路输送状态为研究充填料浆的流变特性提供了一种新的思路。
本文通过室内流变试验获得了某金矿高浓度全尾砂胶结充填料浆的屈服应力和黏度系数等。基于Fluent流体模拟软件建立了与矿山实际管路输送系统1∶1比例的数值仿真模型,模拟了高浓度全尾砂胶结充填料浆在管道中的流动特性,分别计算了不同浓度和配比的充填料浆在管道中的沿程阻力系数,确定了全尾砂胶结充填料浆最大允许充填倍线Nmax和临界输送浓度,数值仿真结果对优化矿山管道输送系统具有重要的指导意义。
2 矿山充填系统现状
某金矿位于山东省胶州半岛,生产规模为5 000 t/d,主要1#、2#矿体赋存于招平断裂带下,采用上向水平分层充填法和上向进路充填法,分级尾砂胶结充填和废石充填。充填系统工艺流程:选矿厂全尾砂经水力旋流器组分级,分级后的底流粗尾砂经渣浆泵泵送至立式砂仓内。分级尾砂在立式砂仓中自然沉降浓缩,底流进入搅拌机与胶结材料搅拌制备后,经由充填钻孔自流输送到采空区进行充填。不需要充填时,选厂全尾砂全部泵送至尾矿库。矿山现有的分级尾砂充填系统主要存在以下问题:
(1)井下充填消耗的尾砂量较少,大部分尾砂需要排至现有尾矿库。按照目前生产规模和充填方式,现有尾矿库仅能服务1~2年,急需要处理更多的尾砂。
(2)分级尾砂胶结充填料浆的质量浓度偏低,在长距离输送过程中离析严重,导致浇面强度达不到无轨设备通行要求,充填料在采场内的泌水率较大,影响了井下环境卫生。
(3)采场底部采用废石充填,充填劳动强度大、安全性差,废石充填成本高。
考虑到矿山现有充填系统处理尾砂的能力有限,为了提高尾砂的综合利用率,减轻尾矿库的库容压力,有必要将现有的分级尾砂充填系统改造高浓度全尾砂充填系统,并对高浓度全尾砂充填料浆的管道输送特性进行研究。
3 充填材料物理特性
充填粗骨料主要来自磨浮厂房的全尾砂,其物理性质、化学成分及粒径分布对充填料浆的性质产生重要的影响。
全尾砂密度测试参考《土工试验规程》SL237—1999进行,采用比重瓶法测量,计算结果见表1。
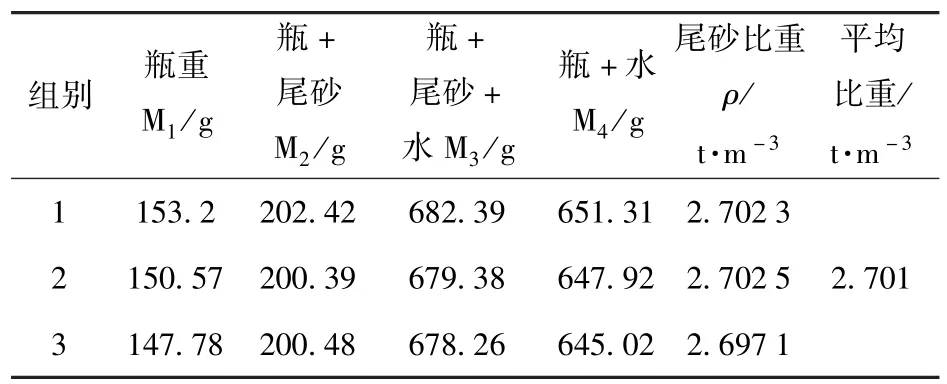
表1 全尾砂密度试验数据
矿床受断裂带的影响,主要赋存在黄铁绢英岩化碎裂岩和黄铁绢英岩化花岗岩中。选厂的尾砂产出率达到95%,全尾砂中SiO2含量占73.5%,属于惰性材料,无碱集料反应。全尾砂的化学成份分析见表2。

表2 化学成份分析表
全尾砂的粒级组成多用不同粒径区段的颗粒重量百分比表示,尾砂的粒级组成对于充填料浆的性质有着重要的影响。全尾砂粒级组成见表3。

表3 全尾砂粒级组成表
由表3可以看出,全尾砂中小于20 μm极细尾砂占比为30.10%,大于74 μm的较粗尾砂约占40.44%,平均粒径为75.36 μm,属于中粗尾砂。Cu=d60/d10=12.27,全尾砂级配Cu>5,说明级配较好,适合作为充填原材料。
4 充填料浆流变特性实验
4.1 实验原理
剪切屈服应力τ和黏度系数η是研究充填料浆流变特性的重要参数。对于非牛顿流体,剪切屈服应力τ主要指充填料浆发生屈服时的正应力,只有当外部施加的外力大于该剪切屈服应力,才能克服料浆中细颗粒絮凝团之间的相互作用,实现充填料浆的流动。充填料浆流动时,必然在浆体内部产生剪应力以阻止料浆的相对运动,料浆流体的这一特性称为黏度。充填料浆的黏度值一般与抵抗流体剪切变形的能力呈正比例关系[3]。
沿程阻力损失则表示为流体克服黏阻力而损失的能量,输送管路越长,所损失的能量越多,是判断充填料浆输送性能的重要因素。
全尾砂充填料浆作为一种复杂的固液两相浓悬浮液体系,在管路输送过程中管壁剪切应力与剪切速率并非遵循简单的线性关系,属于一种屈服伪塑性流体。当全尾砂充填料浆的浓度超过临界浓度值时,剪切应力随剪切速率的变化近似呈线性关系。因此,在工程实践中一般将高浓度全尾砂充填料浆视为宾汉姆流体[4-5]。宾汉姆流体的具有一定的初始剪切应力,低于此值时不会流动,其本构方程如式(1)所示。

式中:τ——管壁剪切应力,Pa;
τ0——初始剪切应力(或剪切屈服应力),Pa;
η——黏度系数,Pa·s;
du/dy——剪切速率,s-1。
根据料浆管道流速的分布,通过沿程阻力计算公式可以推导出不同流量、不同管径输送时充填料浆的沿程阻力损失,其单位长度沿程阻力公式为
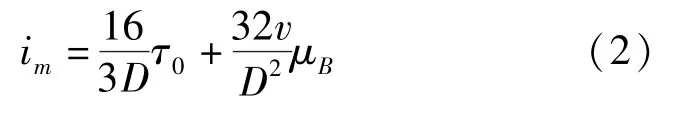
式中:im——单位长度沿程阻力,MPa/m;
D——直管内径,m;
μB——宾汉姆黏度(Pa·s),具有黏度量纲的常数;
v——平均流速,m/s;其中,Q为料浆流量,m3/s。
4.2 实验步骤
实验采用R/S-SST型软固体流变仪测定充填料浆的相应黏度和动态屈服应力,具体如图1所示,测量的数据可以在Rhoe3000软件上进行批量处理。这种测量流变参数的方法灵活简单,数据重复可靠,大大提高了充填料浆流变特性参数的测量精度和效率。该流变仪的基本工作原理是采用动态测定法,设置好剪切速率和测试时间,通过高速电机带动十字形转子旋转,充填料浆对转子施加黏滞阻力,通过仪器内部的传感器元件将这种阻力转换为扭矩和剪切应力,并实时绘制测试充填料浆的流变特性曲线图,利用宾汉姆模型、H-B(赫歇尔-伯克利)模型或自定义模型对监测的数据进行拟合,得到浆体的流变本构关系方程。

图1 RST-SST流变仪
根据已经完成的塌落度试验和强度配比试验,分别配置浓度为68%、70%、72%、74%,灰砂比为1∶6、1∶10的全尾砂胶结充填料浆作为本次流变试验测试对象,另外配置浓度为70% ~76%的全尾砂料浆作参考。胶凝材料选用胶固粉。试验温度保持在24℃下进行,尽量减少温度变化对测试结果的影响。图2、图3所示分别为浓度70%、灰砂比1∶6的全尾砂胶结充填料浆黏度和剪切率流变特性曲线图和剪切应力-剪切速率的流变特性曲线图。

图2 黏度-剪切率流变特性曲线图(浓度70%、灰砂比 1∶6)

图3 剪切应力-剪切速率的流变特性曲线(浓度70%、灰砂比1∶6)
4.3 料浆流变参数分析
利用Rhoe3000软件对各组方充填料浆的流变特性曲线进行拟合,可以得到不同组方的全尾砂充填料浆的动态屈服应力τ0和黏度系数η之间的回归方程,具体见表4。可以发现剪切应力与剪切速率基本呈线性关系,回归方程的稳定指数R2大于0.94,可以采用宾汉姆流变模型来描述该矿全尾砂充填料浆的流变特性。
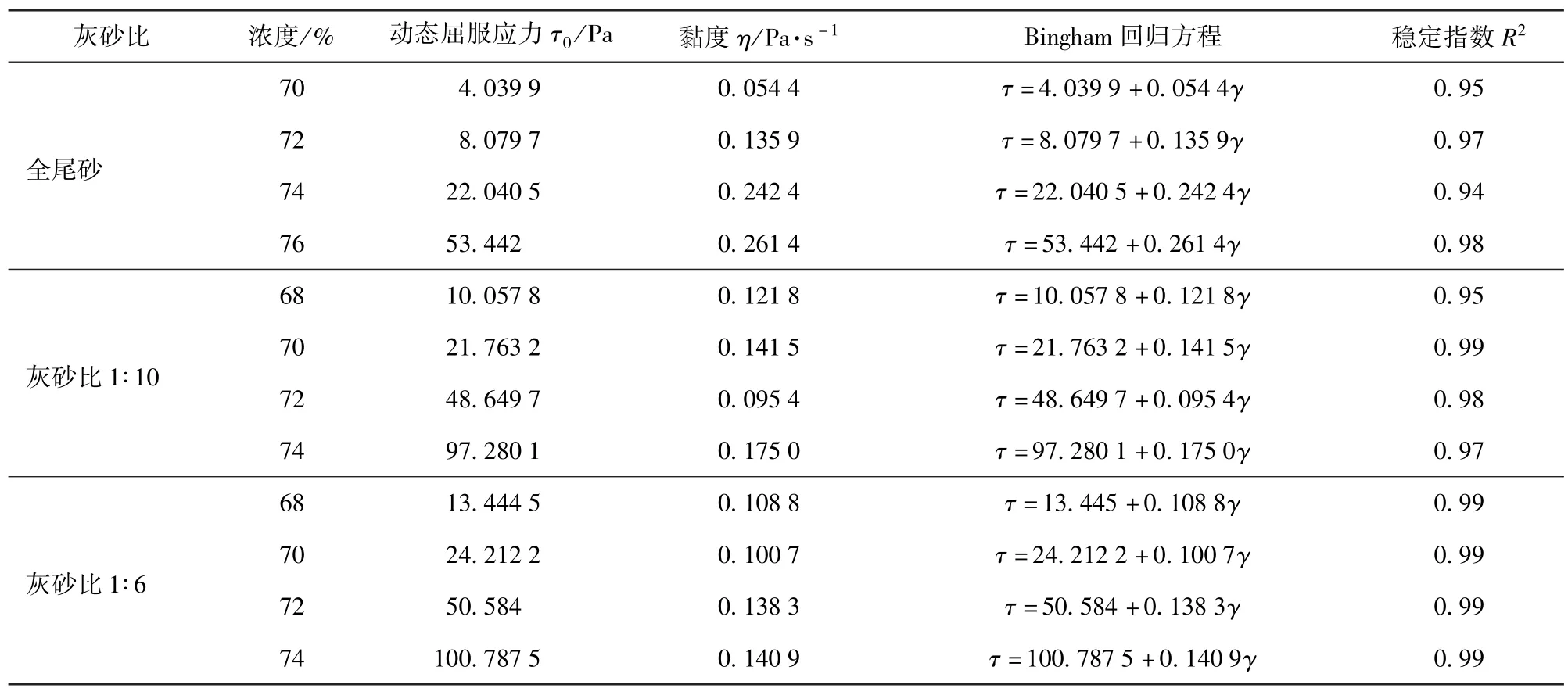
表4 不同组方充填料浆Bingham流变模型回归表
从表中也不难看出,充填料浆的动态屈服应力τ0随着质量浓度的不断增加而增大,这是因为充填料浆中含有正负电荷颗粒互相吸引,当质量浓度越大时,含有的颗粒数量越大,颗粒在料浆中形成的絮团结构需要施加一定的抗剪能力才能使料浆流动,即需要克服料浆的屈服应力。
充填料浆的动态屈服应力随着灰砂比的增加表现出增加的趋势,尤其在胶结充填料浆与全尾砂非胶结充填料浆之间,这种现象表现的更为明显。这是因为胶凝材料相对全尾砂的粒径较细,具有更大的比表面积,粒子之间有更大的相互作用的面积,进而表现出更高的屈服应力和黏度,灰砂比1∶6与灰砂比1∶10的充填料浆之间的屈服应力值差异相对很小。
5 基于FLUENT的管道输送数值仿真
5.1 模型建立
随着计算机技术、数值仿真技术的发展,目前模拟充填管路输送过程的软件主要有FLUENT、FLOW-3D及FLOTRAN等,其基本原理是通过数值求解控制流体流动的微分方程,得出流体流动的流场在连续区域上的离散分布,从而近似模拟流体流动情况[6]。
本次试验利用FLUENT软件建立该金矿的充填管路输送系统。该软件可以可以根据雷诺数Re精确地模拟无黏流、层流、湍流等模型,也可以根据需要自定义流变模型。Fluent软件的求解步骤一般需要通过几个基本步骤,并提供相关的参数或物理量。
(1)通过 Solidworks或者 SpaceClaim等建模模型。
(2)采用ICEM或Meshing等划分网格。
(3)针对模型的特征,运行合适的解算器:2D、3D、2DDP、3DDP。
(4)输入网格文件msh,检查网格,如果出现负体积的情况则需要进行检查修改。
(5)根据流体的特征,比如可压缩流或不可压缩流、定常状态或非定常状态等,从而选择解的格式。
(6)选择需要解的基本方程:层流还是湍流、化学组分还是化学反应、热传导模型等。
(7)设置材料的属性,包括比重、黏度等参数设定。
(8)指定操作环境、边界条件,调节解的控制参数,以达到预期的效果。
(9)初始化流场,进行迭代,迭代结束后检查、保存结果。
井下充填管路直径146 mm,壁厚12 mm,充填管路总长3 148 m。本次管道输送模拟仿真试验利用Solidworks前处理软件建立充填管路模型,利用Meshing工具将管路划分六面体结构网格,按照矿山真实的充填管路建立1∶1比例的输送仿真模型,如图4所示,模型中共划分为 10段管道,长度3 148 m,网格数量共计881 244个。

图4 三维充填管道数值仿真模型
5.2 基本假设与边界条件
1)基本假设
鉴于充填料浆在管路输送过程中的流变性及管路输送工艺的复杂性,需要根据实验目的确定主要影响因素,简化其他因素。对充填料浆和管路的相关特性进行必要的说明和假设:
(1)充填料浆的黏性不随温度、时间的变化而变化。
(2)充填料浆为宾汉姆体模型且不可压缩。
(3)不考虑采矿作业扰动等对充填管路的影响。
(4)不考虑与外界环境的热交换。
(5)充填料浆在管道输送过程中处于满管状态。
2)边界条件
将模型入口的inflow流速设置为匀速,流速方向垂直于管道的横截面,出口方向设置为outflow。管道壁面采用无滑移边界条件。采用自流输送方式,入口压力为标准大气压力。设置Z方向的重力加速度值为-9.8 m/s2。
模拟工况同表4中的各组数据,流量设置为80 m3/h,充填管路净直径122 mm,对应的流速为1.90 m/s,并输入各组方的料浆容重ρj。
5.3 模拟结果分析
1)灰砂比对沿程阻力损失的影响
图5所示分别为全尾砂、灰砂比1∶10、灰砂比1∶6,质量浓度72%的充填管路压力分布云图。从图中可以发现从地表140 m到井下-380 m水平,竖直管路的压力从上到下逐渐增大,在-380 m水平竖直弯管处压力达到最大值。由黏性流体的伯努利方程(式3)可知,重力势能在克服管路沿程阻力损失hw后,竖直管路的压力逐渐增加,在弯管处流体的动能最大。因此,在日常生产管理过程中,需要加强弯管处的管路监测和维护,防止管路过度磨损或发生堵管事故。水平管路由于存在沿程阻力损失hw,在重力势能维持不变的情况下,充填管路的压力逐渐减小,可以起到水平管路充填减压的作用。

图5 不同灰砂比下充填管路压力分布(质量浓度72%)
黏性流体的伯努利方程见式(3)
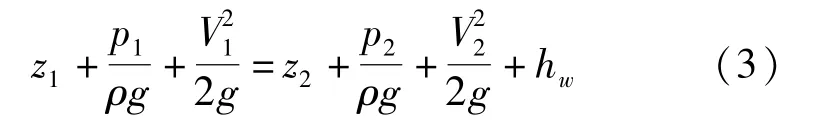
式中,Z1、Z2分别为单位质量流体的位能,p1/ρg称为流体功分别为单位质量流体的动能,hw为阻力损失。
从全尾砂到灰砂比1∶10、灰砂比1∶6变化时,充填管路出口处的压力从12.47 MPa、7.98 MPa到7.07 MPa逐渐减小,沿程阻力损失则逐渐增大。主要是因为细粒径胶凝材料比表面积大,随着胶固粉的增加,充填料浆的屈服应力相应增加。
2)质量浓度对沿程阻力损失的影响
图6所示为灰砂比为1∶6,质量浓度分别为68%、70%、74%时的充填管路压力分布云图。从图中可以发现,随着充填料浆质量浓度的增加,出口处的压力值大幅度降低,沿程阻力损失大幅度增加。即充填料浆的质量浓度与沿程阻力损失成正比例关系。

图6 不同质量浓度下充填管路压力分布(灰砂比1∶6)
3)自流输送可行性验证
为了满足充填料浆的自流输送,一般需要满足一定的高差,在充填料浆输送时产生一定的势能来克服充填管路的阻力。充填系统应满足以下条件

式中,H是充填料浆入口和出口的垂直高差,m;ρj为料浆密度,t/m3;im为阻力损失,kPa/m;L为充填管路总长度,m。
当重力势能大于沿程阻力损失时,充填料浆可以实现自流输送,反之则需要泵压输送。
表5中对充填管路输送的数值仿真结果与室内流变试验的结果进行了对比验证,结果表明两种计算方式的误差控制在10%以内,说明数值仿真模型计算的结果精确度较高,仿真结果对于优化矿山充填系统具有重要的指导意义。表5中的各组方充填料浆的沿程压差均为正值,可以实现自流输送,无需泵压输送。

表5 充填料浆管路输送沿程阻力损失验证
4)充填料浆临界输送浓度确定
充填倍线是表征充填系统料浆输送的重要参数。为保证充填料浆顺利实现管道自流输送,几何充填管路倍线N要小于最大允许充填倍线Nmax。
最大允许充填倍线Nmax是根据砂浆水力坡度和浆体容重计算的,实际应用中可按式(5)估算:

式中:K3——垂直管段的满管系数,取0.9;
γj——砂浆容重,t/m3;
K4——管道局部阻力系数,取1.1;
im——砂浆水力坡度(阻力损失),104Pa/m。
根据该金矿现有的充填管路系统布置情况,充填倍线普遍为2.5~4,部分采场最大达到4.6。由式(5)计算各料浆组方的最大允许充填倍线Nmax,结合表5中的数据,最终确定全尾砂胶结充填料浆的临界输送浓度为72%,具体数据见表6。对于偏远采场,需要适当降低输送浓度满足自流输送的要求。

表6 全尾砂胶结充填料浆临界输送浓度
6 结论
(1)为了提高尾砂的综合利用率,减轻尾矿库的库容压力,需要将现有的分级尾砂充填系统改造为高浓度全尾砂充填系统。
(2)对全尾砂的物理特性进行分析,全尾砂的平均比重为 2.701 t/m3;全尾砂中 SiO2含量占73.5%,属于惰性材料,无碱集料反应;全尾砂级配Cu>5,级配较好,属于中粗尾砂,适合作为井下充填原材料。
(3)利用流变仪对全尾砂充填料浆的黏度和动态屈服应力进行测定。研究结果表明高浓度全尾砂充填料浆符合非牛顿流体中宾汉姆流体的特征。充填料浆的动态屈服应力τ0随着质量浓度和灰砂比的不断增加而增大。
(4)基于Fluent软件建立了与矿山实际充填管路输送系统1∶1比例的数值仿真模型,分别模拟了不同浓度和配比的充填料浆在管道中的流动特性和沿程阻力损失情况,模拟结果表明,沿程阻力损失与料浆质量浓度和灰砂比呈正比关系,浓度越大,阻力损失越大;灰砂比对沿程阻力损失的影响较小。
(5)数值仿真结果与室内流变试验结果进行对比验证,结果表明用Fluent软件建立的管道输送数值仿真模型的精确度较高。通过数值仿真手段可以节约矿山的试验成本,仿真结果对于优化矿山充填系统具有重要的指导意义。
(6)根据沿程阻力损失的计算结果,计算各组方充填料浆的最大允许充填倍线Nmax,并确定全尾砂胶结充填料浆的临界输送浓度为72%,为矿山下一步全尾砂充填系统设计提供了可靠的数据支撑。

