利用Python编程实现基于EGM2008模型的高程异常计算*
吴 勇,常燕敏
(四川省地质矿产勘查开发局测绘队,四川 成都 610017)
0 引言
全球导航卫星系统(GNSS)以其定位快、精度高等优势在测绘、水利、交通、资源调查等领域被广泛应用,特别是连续运行参考站(CORS)已经成为外业数据采集的主要测量手段[2],但在高程方面,GNSS提供的不是正常高,而是大地高。将大地高转换成正常高,关键是高程异常的求解。高程异常分解成长波项、短波部分和残余部分,利用美国国家地理空间情报局(National Geospatial-intelligence Agency,NGA)研制的全球超高阶地球重力场模型EGM2008,能够精确表达高程异常的长波项,地形变化引起的短波部分可以利用剩余地形模型计算所得[3],也可以利用数字高程模型(Digital Elevation Model,DEM)格网数据求解所得。本研究主要运用在地形起伏不大,满足一定范围内的测绘需要,因此不单独考虑短波部分,将高程异常分解为高程异常长波项和残余高程异常值。采用“移去-拟合-恢复”法的思想,利用Python编程实现高程异常长波项的计算以及利用测区内极少数的GNSS水准点的残余高程异常值和一定的拟合函数计算出待求点的残余高程异常,从而求得待求点的高程异常值。
1 原理与方法
本文选择 “移去-拟合-恢复”法求解高程异常,高程异常值分解为高程异常长波项(ζEGM)和残余高程异常值(ζres)。高程异常ζ可以表示为:
ζ=ζEGM+ζres
(1)
高程异常长波项(ζEGM)可以利用EGM2008模型计算求得,残余高程异常值(ζres)需要利用测区内已知点的残余高程异常值通过数学函数拟合求得。
根据 “移去-拟合-恢复”的思想,先利用EGM2008模型计算已知GNSS水准点的高程异常长波项(ζEGM)[2],从已知点的高程异常(ζ)中移去已知点的ζEGM,获得已知点的ζres,将已知点的ζres代入数学函数中计算出拟合系数。
再利用EGM2008模型计算待求点的高程异常长波项(ζEGM),利用数学模型和拟合系数计算待求点的残余高程异常值(ζres)。将待求点的高程异常长波项和残余高程异常值相加,从而求得待求点的高程异常值(ζ)。具体处理流程见图1。

图1 高程异常计算流程图Fig.1 Flow of height anomaly calculation
1.1 求解高程异常长波项
EGM2008重力场模型使用了最先进的算法与建模技术,以 PGM2007B 模型( PGM2007A 的变种模型)为依据,计算中采用了 GRACE 重力卫星数据、全球5′×5′重力异常数据、TOPEX 卫星测量得到的高程数据、地形数据[3]。目前 EGM2008 全球重力场模型是使用最广泛的重力场模型,阶次完全至2 159。目前可用通过NGA网站下载1′×1′分辨率的格网数据,是目前计算高程异常长波项最理想的模型。
利用EGM2008模型来计算高程异常长波项可以采用现有的软件(Alltrans EGM2008 Calculator)计算,该软件调用1′×1′或10′×10′分辨率的格网数据插值计算出高程异常长波项[3]。考虑到程序的实用性和计算数据格式统一性,况且1′×1′分辨率的格网数据量较大(约980 M),不方便程序运行,因此本文编写的程序没有直接利用EGM2008模型求取高程异常长波项,而是利用Alltrans EGM2008 Calculator 1.2软件导出计算区域内各格网点的高程异常长波项数据,从格网点的高程异常值长波项数据中通过移动二次曲面拟合求得待求点的高程异常长波项。
在Alltrans EGM2008 Calculator 1.2软件的“Grid-area”选项输入需要求取高程异常值区域的纬度和经度范围。在“spacing”选项输入格网间距,可以根据计算精度选择不同的格网间距,点击“Calc!”即可导出每个格网点的高程异常长波项数据文件。如图2所示,左边是格网数据导出界面,在该界面中输入相应的参数,右边则是导出后的格网数据,即是本程序计算时需要调用的数据。

图2 导出格网数据的界面和导出后数据格式Fig.2 Interface for exporting grid data and exported data format
1.2 求解残余高程异常
待求点残余高程的求解主要分成两步进行,先利用已知点的残余高程异常值计算拟合函数的系数,再将待求点的数据代入拟合函数中计算出待求点的残余高程异常值。
1)根据式(1)可以计算出已知GNSS水准点的残余高程异常值。即残余高程异常值由高程异常值(ζ)减去高程异常长波部分(ζEGM),而高程异常值(ζ)由已知的大地高减去正常高。再将已知点坐标x,y和残余高程异常值代入拟合函数计算出拟合系数。可以根据测区的地形起伏、已知点分布和测区形状选择适当的拟合函数进行拟合,常用的数学函数有曲面函数、平面函数、线性函数,各种函数都有一定的局限性和使用范围,将在后面详细叙述。
2)将待求点坐标x,y代入上一步选择的拟合函数中,即可求出待求点的残余高程异常值。因本次测试数据所在区域高程起伏不大,不是带状分布,因此本文只利用了二次曲面拟合函数进行验证。在实际使用时可根据求解范围、区域地形起伏和已知点数据分布情况选择不同的数学函数进行拟合。
多项式曲线拟合主要是运用在线路上的高程控制点拟合,控制点呈狭长的带状分布,可看作一条曲线,因此选用一个多项式作为差值函数。残余高程异常值ζres与坐标xi(或yi,i=1,2,…,n)之间函数关系,可用多项式曲线拟合表示为:
(2)
式中:a0,a1,…,am为待定系数。
平面拟合法主要运用于小区域且地势较为平坦的区域,类似于利用平面区代替局部的似大地水准面。平面拟合表达式为:
ζres=a0+a1x+a2y
(3)
式中:x、y为点的坐标;a0、a1、a2为模型参数。
二次曲面拟合主要运用在地形起伏不大,控制点较少的情况下。因为二次曲面拟合的模型比较平滑,可以认为在一定范围高程异常是平缓的变化。二次曲面函数表达式为:
ζres=a0+a1x+a2y+a3xy+a4x2+a5y2
(4)
式中:x、y为点的坐标;a0、a1、a2a3、a4、a5为模型参数。
2 编程实现高程异常值计算
2.1 计算高程异常长波项
读取计算点的经纬和纬度,以计算点为中心在格网高程异常长波数据文件中搜索出距该点最近的12个格网点的数据,建立一个拟合曲面,即将这12个点的数据代入式(4)中求解出拟合系数a0、a1、a2、a3、a4、a5。再将计算点的经度、纬度和拟合系数代入式(4)中,求解出待计算点的高程异常长波项。
2.1.1搜索最近格网点
按行循环读取格网高程异常长波数据,调用距离计算函数(get_dist)计算每个格网点到计算点的距离,将距离计算结果添加到列表中,直到添加的距离个数等于K(搜索格附件网点个数)值时,再将计算的结果与列表中的最大值进行对比,如果小于列表中的最大值就将该值替换列表的最大值,实现代码如下:
for xx in B_L_z:
x=float(xx[0])
y=float(xx[1])
dist_1=get_dist(b,l,x,y)
if len(x_y_z) < k:
dist_all.append(dist_1)
x_y_z.append(xx)
else:
if dist_1 < max(dist_all):
site=dist_all.index(max(dist_all))
dist_all[site],x_y_z[site]=dist_1,xx
2.1.2计算函数拟合系数
主要调用 Python 的leastsq库对给定的三维数据点进行最小二乘拟合,需先定义拟合函数和错误函数,利用numpy库读取已知点数据,实现代码如下:
def func(p,x,y):
a,b,c,d,e,f=p
return a*x**2+b*y**2+c*x*y+d*x+e*y+f
def error(p,x,y,z):
return func(p,x,y)-z
b=np.loadtxt(file_path,delimiter=′,′)
Xi=b[:,0]
Yi=b[:,1]
Zi=b[:,2]
Para=leastsq(error,p0,args=(Xi,Yi,Zi))
a,b,c,d,e,f=Para[0]
3 案例计算
3.1 高程异常长波项精度检验
为验证本软件高程异常长波项计算的可靠性,本次测试数据采用某市1′×1′的网格点坐标。该市最高点海拔为4 984.1 m,最低点海拔为308 m。共测试30 691个坐标点,测试前利用Alltrans EGM2008 Calculator软件分别导出0.5′×0.5′和1′×1′的格网点高程异常长波数据,自编软件分别调用这两种分辨率的格网数据对待求点进行计算,求得高程异常长波项。再利用Alltrans EGM2008 Calculator软件中批量转换获得的高程异常值长波项与本软件计算所得的高程异常长波项进行对比。表1列举了部分点高程异常长波项不同软件计算的结果。
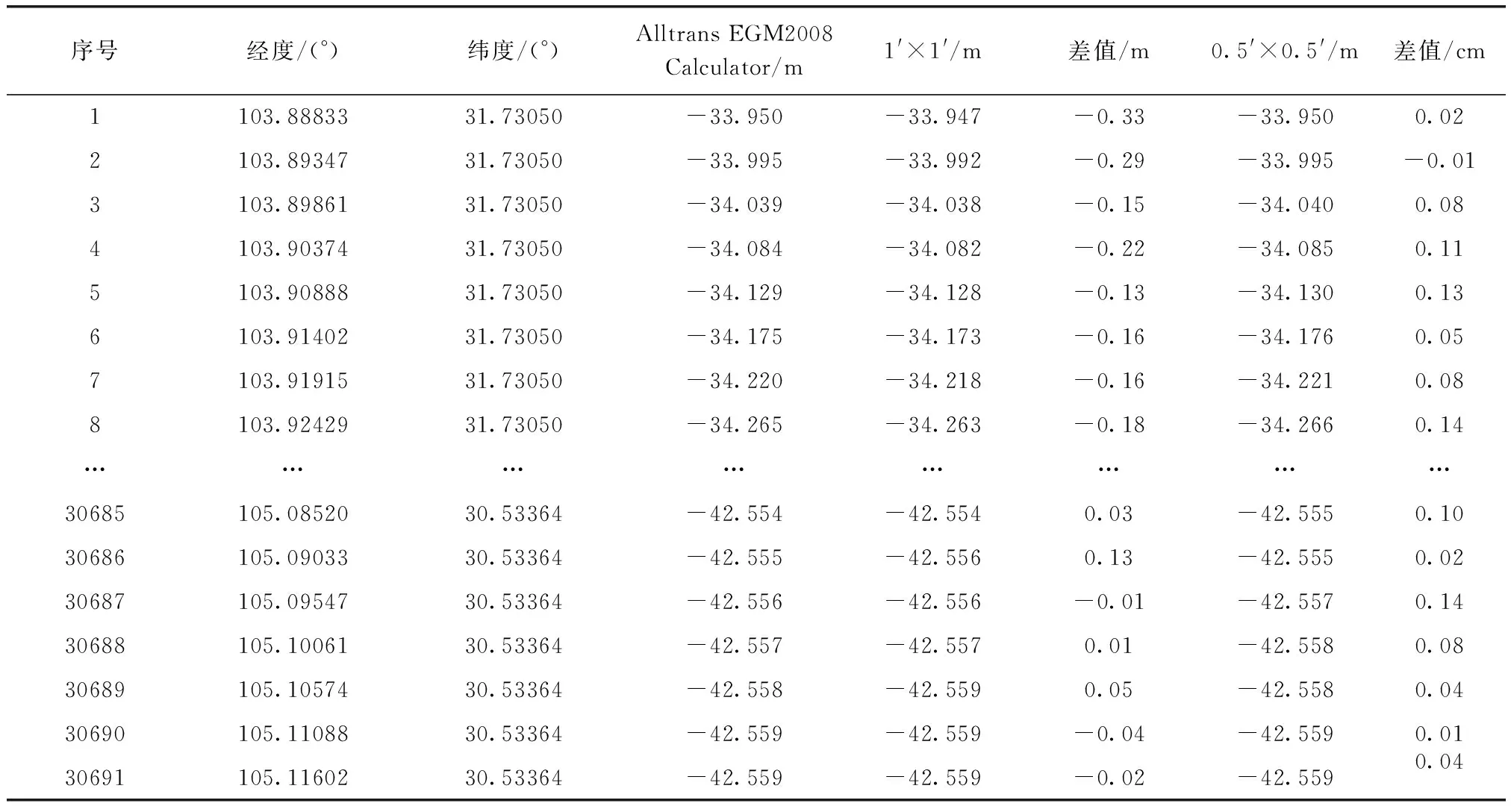
表1 部分点高程异常长波项计算对比表Tab.1 Comparison of long-wave component calculations for height anomalies at selected points
从表1中可以看出:采用1′×1′的格网数据计算的数据与Alltrans EGM2008 Calculator软件计算所得的差值最大为7.12 cm,中误差为1.85 cm。而采用0.5′×0.5′的格网数据计算的值与Alltrans EGM2008 Calculator1.2软件计算所得的差值最大为4.65 cm,中误差为0.98 cm。中误差均小于4.0 cm,满足区域似大地水准面精化基本技术规定中的城市级别的精度要求,因此本文提出的计算方法能满足高程异常的长波项计算。本文也对差值在不同区间段的数据进行统计,如图3所示。根据统计分析得知,采用0.5′×0.5′的格网数据计算的结果明显优于采用1′×1′的格网数据计算的结果,因此在实际生产运用中建议采用0.5′×0.5′的格网数据来计算高程异常的长波项,若只是满足等外水准的精度要求,也可以采用1′×1′的格网数据来计算。

图3 长波项差值在不同区间的统计图Fig.3 Statistical chart of long-wave component differences in different range of values
3.2 以某市各区县的控制点数据计算为例
某市总面积为5 911 km2,呈西北至东南的蚕形,西北为山区,中部为平原,东南是低山丘陵。考虑到西北山区没有收集到控制点,因此只利用了中部和西南地区共13个C级GPS点(同时具有正常高数据和大地高数据)作为已知点,控制区域约4 745 km2。点位分布如图4所示,已知点数据分布比较均匀,基本能覆盖整个计算区域。数据中最大高程为763.502 m,最小高程为398.234 m。考虑到本计算区域地势起伏不大,已知点数据也大于6个,因此计算采用二次曲面拟合函数进行计算,根据式(1)计算得出这13个已知点的残余高程异常最大为22.16 cm,最小为5.11 cm。利用该已知点数据计算二次曲面拟合函数的5个系数。表2列举了部分已知点数据的计算成果。

表2 部分已知点数据计算结果Tab.2 Data calculated results for some known points

图4 控制点和检核点分布图Fig.4 Distribution of control points and check points
利用实测的182个三等GPS水准点(同时具有正常高数据和大地高数据)作为检核数据,检核数据中最大高程为718.583 m,最小高程为329.472 m。将检核数据的高程异常视为真值。利用本程序计算的高程异常值与真值对比,最大差值为5.86 cm,最小差值为0.007 cm,中误差为2.56 cm,满足城市测量规范中的卫星定位高程控制测量中的相关要求。图5列出了差值分布在不同区间的个数,其中差值小于3.0 cm占比80%,证明本文的计算方法和自编程序计算的结果比较可靠。

图5 高程异常值的差值在不同区间的统计图Fig.5 Statistical chart of height anomaly differences in different range of values
4 结束语
根据“移去-拟合-恢复”的计算流程,本文提出了基于EGM2008模型,利用Alltrans EGM2008 Calculator软件导出高程异常格网数据,再利用自编程序利用高程异常格网数据计算出待求点的高程异常值数据,然后利用少量已知点的残余高程异常通过一定的拟合函数计算出待求点的残余高程[4],根据式(1)即可求得待求点的高程异常。通过与某市的实测数据对比,结果表明本文的计算方法和程序能满足大部分测绘工程的需求。本文未考虑地形因素的影响,如计算区域的地形起伏较大还应考虑地形因素的影响,后期将进一步完善程序,将地形影响因素也纳入程序中。

