考虑负荷多无功用电场景的城市配电网无功优化配置

杨秀，焦楷丹，孙改平，陈小毅，杜佳玮，仇志鑫

(1.上海电力大学电气工程学院，上海市 200090；2.国网上海浦东供电公司，上海市 200122)

0 引 言

近年来，在能源转型与科技进步的推动下，电力电子设备在电力系统中的应用取得了长足发展，一方面体现在大量特性各异的分布式发电、小型储能以及电动汽车等通过电力电子接口接入系统[1]，另一方面体现在大量含电力电子装置的新型负荷广泛接入配电网用户侧。高比例电力电子设备不仅使用户的负荷结构发生变化，也深刻改变着电力系统中负荷的无功特性，主要表现在用户的功率因数在不同时段变化明显，节点电压波动严重，越限的可能性增加[2]。此外，未来城市配电网电缆化率不断提升也会加重配电网的无功问题[3]。为适应高比例电力电子设备和高电缆化率的新型城市配电网安全经济运行需求，在无功补偿规划阶段必须考虑负荷无功用电变化的影响，研究考虑负荷无功用电不确定性的配电网无功优化配置。

配电网无功补偿优化配置的目的是在满足各种运行方式与约束条件下确定无功补偿装置的最优安装位置和容量，对降低线路损耗、稳定节点电压具有重要意义[4]。近年来，考虑不确定性的配电网无功优化配置问题受到广大学者的重视。文献[5]建立了两阶段随机优化调度模型，以提高系统对不确定负荷的适应性，但该模型的第二阶段依赖于日前风机出力预测和负荷预测。文献[6-7]建立了基于机会约束的配电网随机优化模型，将约束区间放大至某一置信区间，借助概率潮流求解，该方法能够有效减小负荷波动性对无功优化配置的影响。文献[8-9]用梯度模糊数来描述负荷的不确定性，构建多目标模糊优化模型，分别用降半Г型与降半直线型形成模糊目标函数，最后得到在不同运行方式下、不同负荷水平下的无功补偿最优值。但机会约束与模糊模型均改变了确定性无功优化模型[10]，且求解难度大。文献[11-12]建立了无功配置的两阶段鲁棒优化模型，两阶段交替进行，最终搜索到满足光伏与负荷出力最恶劣时节点电压不越限的控制变量取值，在保证电力系统安全运行方面有较好效果。但鲁棒优化是以最坏情况下的优化为基础，得到的最终结果保守且不一定最优。文献[13-15]利用场景分析法处理不确定性问题，用概率分布来体现不确定性，从而将不确定模型转换为多个场景下的确定模型。通过对场景进行合并缩减，分别生成风光荷的典型出力场景并综合全年出力水平进行无功补偿规划。与其他模型相比，基于场景概率的优化模型具有更好的精确性与针对性。

以上研究虽然考虑了负荷的波动性与不确定性，但在进行负荷建模时只考虑到负荷有功用电特性，认为在不同时间负荷的功率因数保持不变，并在这个假设的基础上进行无功优化配置。然而，在含有高比例分布式能源与高比例电力电子设备的新型城市配电网中，各类负荷的运行状态变化快，负荷常在轻载、重载甚至过载之间转换，许多设备(如电动机)在不同负载水平下的功率因数差异较大，导致负荷与电网交换的无功功率存在较大的不确定性。因此，考虑负荷无功用电特性，并借助概率建立模型，可以帮助电网人员更精准地制定无功补偿方案，从而提升电网运行的安全性与灵活性。

为此，本文基于随机规划中的场景法，构建考虑负荷无功用电不确定性的多场景期望值无功优化模型。由于负荷无功用电量往往与其有功用电量成正相关，通过负荷无功功率变化曲线无法很好地体现新型城市配电网中负荷的无功用电特性，因此本文采用负荷日功率因数变化曲线来反映负荷无功用电的波动性与不确定性。依据上海市某配电网不同类型用户的无功用电信息，利用大数据平台采集到的实际负荷数据，通过日功率因数变化曲线的组合场景及其概率来反映负荷无功用电的特征。首先，本文利用多重一维卷积自编码器(one-dimensional convolutional autoencoders，1D-CAEs)对负荷日功率因数变化曲线序列进行降维与特征提取，充分挖掘负荷的历史信息，然后用k-means进行场景缩减，获得不同用户的典型无功用电场景，并组合出多用户的场景集和相应概率，最后采用改进的IEEE 33节点系统验证所提方法的有效性。

1 多无功用电场景的期望值模型

1.1 目标函数

随机优化问题指带有不确定因素的最优化问题，期望值模型将含有不确定因素的目标函数用其数学期望代替，从而将随机规划转化为一个确定的数学规划问题[13]。本文采用场景分析法来描述负荷无功用电的不确定性，场景的概率作用于目标函数，而不直接作用于控制变量[16]，以运行成本的期望值最小为目标，加入节点电压罚函数，来保证在不同负荷场景下电压波动尽可能小，得到目标函数F为：

(1)

式中：ps为组合场景s出现的概率；fs为场景s的优化结果；S为组合场景总数。fs的表达式为：

(2)

式中：c1、c2为电容器、电抗器的单位补偿量价格；QCi、QLi为节点i补偿装置的补偿容量；cf为补偿节点的固定投资费用；NC、NL为安装电容器、电抗器的节点数；c3为电价；Y为投资回收年限；tmax为年最大负荷损耗时间；ΔPloss为减少的有功网损；λ为惩罚因子；UN为节点的额定电压；Ui为节点i的电压；Nover为电压越限的节点数。

1.2 约束条件

1)潮流方程约束。

(3)

(4)

式中：Pi、Qi分别为节点i注入的有功功率、无功功率；θij为节点间的电压相角差；Bij与Gij为节点导纳矩阵元素的实部与虚部；NB为系统母线节点数。

2)不等式约束。

优化模型的约束条件为：

QCi,t,min≤QCi,t≤QCi,t,max,i∈NC,t∈TC

(5)

QLi,t,min≤QLi,t≤QLi,t,max,i∈NL,t∈TL

(6)

Uimin≤Ui≤Uimax,i∈NB

(7)

cosφA,min≤cosφA≤cosφA,max

(8)

式中：QCi,t、QCi,t,max、QCi,t,min分别为第i个节点上电容器容抗及其上下限值；QLi,t、QLi,t,max、QLi,t,min分别为第i个节点上电抗器感抗及其上下限值；TC、TL分别为全天负荷较高与较低的时段；Uimax、Uimin分别为节点i电压的上下限值；cosφA、cosφA,max、cosφA,min分别为平衡节点的平均功率因数及其上下限值，当cosφA在0.95～0.98之间时，系统无功平衡情况较好[17]。

其中式(8)为平衡节点的平均功率因数约束，平衡节点的平均功率因数能够反映配电网的无功平衡[18]，设置此约束是为了限制负荷较低时系统向上级电网倒送无功功率。

2 模型求解

2.1 总体优化框架

由于本文基于场景分析，所以准确地生成用户的功率因数变化场景尤为重要。为了提升场景生成效率，本文采用深度学习中的1D-CAEs网络，对高维的负荷日功率因数序列逐层降维，提取出低维的深层特征；随后将低维数据送入k-means进行场景缩减，形成不同用户的典型功率因数变化曲线类型，根据不同类型在全年中出现的时间，组合形成多用户的无功用电场景集和相应概率。把无功用电组合场景集输入到期望值模型，用综合灵敏度筛选出最优补偿点，使用粒子群算法求解模型，最终得到兼顾多个无功用电场景的无功优化配置方案。主要的优化框架如图1所示。

图1 总体优化框架Fig.1 General optimization framework

2.2 基于1D-CAEs与k-means的无功用电组合场景生成

1)基于1D-CAEs的负荷无功用电特征提取。

自编码器的编码过程能将输入压缩成潜在的低维空间表征，因此在数据降维领域被广泛应用。卷积自编码器(convolutional auto-encoders，CAE)用卷积神经网络代替普通自编码器的全连接网络，利用卷积与池化操作，通过对卷积核的权重系数ω和偏差系数b不断调优来重构数据，最终实现对序列特征的深度挖掘与有效提取。

采用1D-CAEs方法得到的重构序列能够较准确地反映原序列信息[19-20]。利用1D-CAEs对日功率因数曲线降维，其原理如图2所示。CAE(1)的输入为初始的日功率因数曲线序列，经过卷积池化编码和反卷积解码过程训练网络，输出隐含层序列，此为第一重降维结果；将CAE(1)的隐含层输入至CAE(2)，通过编解码训练，输出隐含层至CAE(3)，以此类推；CAE(n)的隐含层序列经过展平层展平，再经嵌入层，最终得到低维的特征序列。

图2 1D-CAEs数据降维原理Fig.2 Data dimensionality reduction principle of 1D-CAEs

2)k-means场景缩减。

本文采用无监督聚类算法中的k-means方法对低维序列聚类，从而实现场景缩减。选择肘方法确定最佳聚类数。聚类数目确定后，k-means算法能够无监督地确定聚类中心，并把每条数据分到距离其最近的聚类中心所代表的类簇中。经过k-means场景缩减，得到不同负荷全年中典型的日功率因数变化场景，结合场景出现的时间，即可得到不同负荷无功用电的组合场景集及其概率。

2.3 基于综合灵敏度的无功补偿点确定

实际配电网节点数目庞大，补偿装置的安装位置将直接影响优化的效率与结果。从优化结果的可行性和运行的经济性出发，不同用电场景下的补偿点应该相同，为了确定出在不同场景下都能最大可能地保证节点电压合格、综合运行成本最低的无功补偿方案，筛选最佳的补偿节点尤为重要。

1)综合灵敏度指标。

综合考虑平均节点电压偏移灵敏度和网损灵敏度能够有效地确定配电网的最优无功补偿点[21]，定义电压灵敏度与网损灵敏度分别为t时刻节点i设有无功扰动q后引起的系统平均电压偏移和网损的变化量，如式(9)、(10)所示。

EUi,t=ΔUave,i,t|ΔQ=0-ΔUave,i,t|ΔQ=q

(9)

EPi,t=Ploss,i,t|ΔQ=0-Ploss,i,t|ΔQ=q

(10)

式中：EUi,t、EPi,t分别为t时刻的电压灵敏度和网损灵敏度；ΔUave,i,t、Ploss,i,t分别为t时刻系统平均节点电压偏移和系统运行总网损。

(11)

(12)

式中：Ui,t为t时刻第i个节点的电压；N为节点总数；Pl,loss,t为t时刻第l条支路的功率损耗；L为系统支路总数。

每个场景下的综合电压偏移灵敏度EUi和综合网损灵敏度EPi定义为：

(13)

(14)

(15)

(16)

式中：kUi,t、kPi,t分别表示t时刻电压偏移与网损占T时段总偏移量与网损总量的比重。引入kUi,t(kPi,t)的目的是为了提高电压偏移(网损)较严重时刻的电压(网损)灵敏度在确定补偿点时的决策度。

节点i的综合灵敏度指标ECi为：

ECi=α1Ui+α2Pi,α1+α2=1

(17)

式中：α1、α2为权重因子；Ui、Pi分别为经标准化处理的指标，标准化公式为

(18)

参照上述对EUi、EPi指标的定义，本文定义了EBi作为附加指标。筛选感性补偿节点时，先选择ECi指标较大的m个点为候选节点，再用EBi指标对候选节点作进一步筛选，计算公式为：

EBi,t=QB,i,t|ΔQ=0-QB,i,t|ΔQ=q

(19)

(20)

(21)

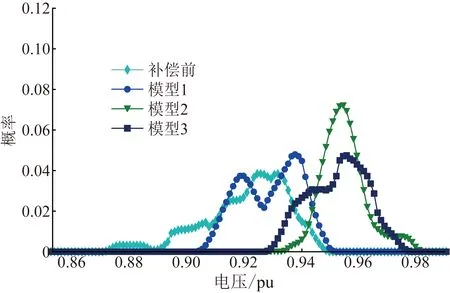
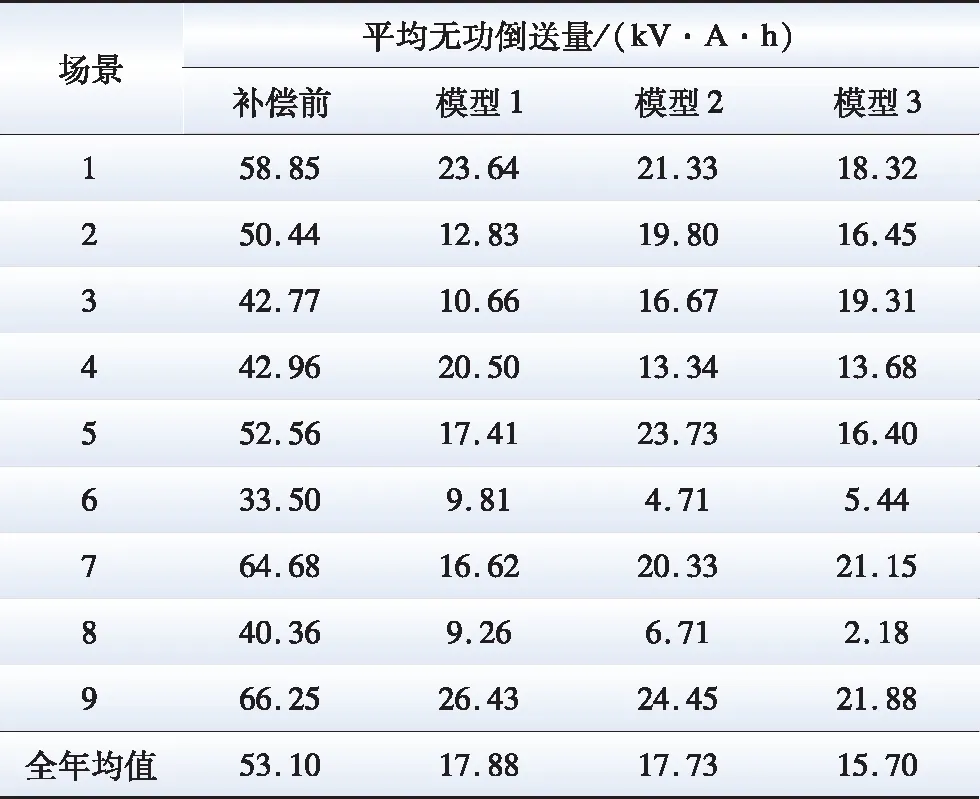
式中：EBi,t为t时刻节点i设有无功扰动后引起的配电网无功倒送量的变化；QB,i,t为t时刻该系统向上级电网倒送无功功率的数值。EBi指标较大的k(k

基于上述方法，在考虑多场景的期望值优化模型中，针对S个用电场景，每个节点可以得到S个综合灵敏度。用每个场景出现的概率乘以节点的综合灵敏度并取和得到综合灵敏度的期望值，由高到低排序，即可确定出期望值模型的最优补偿点。

2)熵权法计算权重因子。

熵权法通过熵值来判断指标的离散程度来计算各个指标的权重，常用来为多指标综合评价提供依据。信息熵的值越小，指标的离散程度越大，说明该指标对综合评价的影响越大。设指标样本数为n，评价指标数为m，根据式(22)计算第j个指标的信息熵ej。

(22)

式中：zij为对xij(第i个样本的第j个评价指标)标准化后的元素；pij为每个元素所占比重。

指标j的权重因子αj的计算公式为：

(23)

2.4 基于粒子群算法的模型求解

粒子群算法被广泛应用于求解非线性规划问题，针对传统的粒子群算法在迭代后期易陷入局部收敛的问题，本文对其参数进行了改进[22]，算法流程如图3所示。

图3 粒子群算法求解无功优化模型流程Fig.3 Flowchart of the PSO to solve the reactive power optimization model

在粒子寻优时，采用分组变化的惯性权重策略，将全部粒子分为两组，分别采取原始线性递减惯性权重ω1与基于反正切函数的非线性递减惯性权重ω2，公式为：

(24)

(25)

式中：ωstart、ωend分别为初始迭代权重和终止迭代权重；gmax、g分别为种群的最大迭代次数和当前迭代次数；k为控制因子。

此外，采用一种线性调整的学习因子策略，学习因子c1与c2更新公式为：

(26)

3 算例分析

选取改进的IEEE 33节点系统进行仿真实验，配电网架空线路全部改为电缆线路，支路电缆选择10 kV三芯交联聚乙烯电缆YJV-3*240，其参数见文献[23]，分布式光伏与负荷接入节点如表1所示。期望值模型中参数的取值：SB=10 MV·A，UB=12.66 kV，补偿装置的补偿容量单价为40元/(kV·A)，补偿节点固定投资费用为5 000元，网损成本为0.45元/(kW·h)，投资回收年限为10 a，最大负荷损耗时间取3 400 h，平衡节点功率因数波动范围为0.95～0.98，平衡节点电压为1.05 pu，其他节点电压范围为0.93～1.07 pu。

表1 分布式光伏与负荷接入情况Table 1 Parameters of distribution PV and load access

3.1 用户典型无功用电场景集生成

本文基于上海市某区域配电网不同用电类型用户2021年全年的实际用电数据建立仿真算例，经过数据预处理后，得到居民负荷、工业负荷与商业负荷各含423、611、740条数据，采样间隔为15 min，即每日包含96个数据。96维的日功率因数序列经过3个1D-CAE层、展平层、嵌入层得到12维序列，特征提取过程如表2所示。

表2 基于1D-CAEs日功率因数序列降维过程Table 2 Dimensionality reduction process of load’s power factor sequence based on 1D-CAEs

3层1D-CAE的卷积层步长为2，填充方式设为VALID，卷积核数量分别为32、64和128，卷积核大小为3。采用Adam优化器，学习率设为0.001，批尺寸设为64，迭代次数为500次，通过最小化均方误差损失函数对每层自编码器进行训练。

将低维数据送入k-means进行场景缩减，依据曲线的变化形态聚类，3种负荷日功率因数变化曲线聚类结果如图4所示，其中工业负荷共聚为3类，分别占总数据的0.337、0.230与0.443；居民负荷共聚为3类，分别占总数据的0.706、0.075与0.219；商业负荷共聚为4类，分别占总数据的0.649、0.081、0.205与0.065。经过场景缩减最终得到3种负荷的典型无功用电场景如图5所示。根据不同场景出现的时间，对用户的无功用电场景进行组合，共得到36个组合场景，但其中27个场景出现天数小于10天，因此最终确定出9个场景及其在全年中出现的概率，如图6所示。

图4 负荷日功率因数变化曲线聚类结果Fig.4 Clustering results of load power-factor curve

图5 负荷的典型无功用电场景Fig.5 Typical reactive power scenarios of loads

图6 无功用电组合场景Fig.6 Combination scenario sets

从图4—6的聚类与场景缩减结果显示，在新型城市配电网中，负荷的无功用电行为多样，不仅在全年不同时间的功率因数变化形态不同，在全天不同时段的功率因数波动也十分明显。可见，当前城市配电网负荷无功用电存在较大的不确定性。

3.2 无功补偿点筛选

系统平均无功用电量与线路充电功率如图7所示。在一天当中，09：00—21：00时段系统无功用电量较高，此时段应进行容性补偿；23：00—次日07:00，系统无功用电量较低，此时段应进行感性补偿，从而减小无功倒送。采用2.3节所述方法确定最优无功补偿点，取扰动ΔQ=0.003 pu，每个场景选取综合灵敏度较大的10个节点作为候选节点。结合每个场景出现的概率，最终确定期望值模型的容性补偿点为节点7、10、16、24、26、31，感性补偿点为节点7、9、16、26、31。

图7 线路充电功率与系统平均无功用电量对比Fig.7 The line charging power and the system average reactive power

3.3 结果分析

为了突出本文提出的无功补偿模型的优越性，共建立3种优化模型，分别比较其运行的经济性与可靠性。

模型1：假设负荷功率因数保持不变的传统优化模型，只考虑负荷有功用电的变化，用每个场景的功率因数均值计算负荷的无功用电量；

模型2：考虑负荷全天功率因数变化的优化模型；

模型3：本文提出的考虑多无功用电场景的期望值模型。

模型1与模型2都不考虑场景出现的概率，以运行成本最小为目标，对每个场景分别进行优化配置，目标函数如式(27)所示，约束条件如式(3)—(8)所示。

(27)

3.3.1 经济性分析

利用粒子群算法求解优化模型，得到每个模型的无功补偿方案如表3、4所示。

表3 各节点电容器配置情况Table 3 Capacitor capacity of each model

表4 各节点电抗器配置情况Table 4 Reactor capacity of each model

由表3、4可知，模型3的补偿点比模型1减少了4个，比模型2减少了5个，容性补偿量分别减少了290、555 kV·A，感性补偿量分别减少了265、665 kV·A。在补偿投资费用上，模型3比模型1和模型2分别节省了4.18万与8.60万元。模型1与模型2按照9个场景分别进行补偿点筛选和补偿容量确定，为保证各场景都能符合系统运行要求，将每个场景补偿节点的集合取并集，并按照补偿容量最大的情况进行配置，该配置方案对应的场景往往是较劣场景，从而导致补偿点较多，且对大部分场景而言补偿容量偏大。而模型3同时考虑负荷多无功用电场景，结合场景出现概率，以综合灵敏度的期望值作为筛选补偿点的标准，该方法相比模型1与模型2能够过滤掉非必要的补偿点，因此补偿点较少，实现对系统更精准的无功配置，避免补偿容量不足或冗余。

基于表3、4的补偿结果，不同场景平均网损以及网损每年产生的费用如表5、6所示。

由表5、6可知，3种模型都能减少有功损耗，平均网损比补偿前分别减小了38.72、45.48、48.00 kW·h，每年由网损产生的费用较补偿前分别减少了65.81万、77.34万、81.60万元。对比3个模型在不同场景中的降损效果，模型1在9个场景中都处于较差水平，说明按照负荷全天功率因数不变的假设进行补偿配置，应用在实际系统中尽管能在一定程度上减少网络损耗，但与其他模型相比还存在很大的提升空间。可见，目前多数学者建立的优化模型存在局限性，无法适应新型城市配电网运行的灵活性与多变性。模型2在3个场景中占优，出现的概率总和为0.236，模型3在6个场景中占优，出现概率为0.764，说明将场景概率考虑进优化模型能够在无功补偿投资最小的前提下，保证全年中大部分用电日的网损最低，发挥无功补偿的最大效益。

表5 不同模型平均网损Table 5 Average network loss of different models

表6 不同模型所需费用对比Table 6 Cost of different models

3.3.2 电压水平分析

采用不同补偿方案得到16：00—21:00时段的平均电压波动幅度如表7所示，各节点在不同场景的平均电压对比如图8所示。

表7 不同模型平均电压波动幅度Table 7 The average voltage fluctuation range of different models

图8 不同模型9个场景各节点平均电压对比Fig.8 The average voltage of nodes in 9 scenarios of different models

由表7和图8可知，补偿前系统的电压水平较低，全年内电压幅值波动严重。3种补偿模型中，模型1的调压效果最差，无法改善无功特性多变的新型城市配电网电压波动大的问题，且在某些极端场景下节点电压越限严重；模型2针对每一种场景分别进行了补偿配置，最终确定的补偿容量偏高，因此能够较好地提高系统节点的电压水平，电压幅值相对较高且波动小；模型3的电压波动相比模型2较大，并且越靠近线路末端的节点电压波动越明显，但是基本能够满足电压合格。图9与图10分别是16:00—21：00节点16与节点31电压幅值在全年中的概率分布。

图9 节点16电压幅值的概率分布Fig.9 Probability distribution of voltage amplitudes at node 16

图10 节点31电压幅值的概率分布Fig.10 Probability distribution of voltage amplitudes at node 31

分析图9、10，补偿前节点16与节点31全年的平均电压分别只有0.920、0.912 pu，电压不合格率为69.34%与88.22%，波动区间分别为(0.865，0.942) pu和(0.872，0.948) pu。采用模型1时，2个节点的平均电压分别为0.925、0.928 pu，不合格率分别为48.82%与63.72%，可见使用该方法无法达到系统稳定运行的需要；模型2两个节点的平均电压分别为0.955、0.949 pu，波动区间分别为(0.934，0.980) pu和(0.935，0.965)pu；模型3两个节点的平均电压分别为0.952、0.945 pu，波动区间分别为(0.930，0.977)pu和(0.927，0.964)pu。通过比较分别采用模型2和模型3进行无功补偿后2个节点电压全年的概率分布，发现采用模型3进行优化的末端节点电压在用电量高的时刻波动略大于模型2，可能会出现电压越下限的情况(如节点31)，但出现的概率只有1.5%左右，全年最多6天的用电高峰时段电压不合格。

3.3.3 无功倒送水平分析

不同模型在01：00—05：00的平均无功倒送量如表8所示。

表8 不同模型平均无功倒送量Table 8 Average reactive power reverse of different models

由表8可知，3种模型都能在不同程度上改善无功功率倒送的现象。其中，模型3的改善效果最好，平均无功倒送量由补偿前的53.1 kV·A·h降低至15.7 kV·A·h。图4—6的聚类结果能够发现在负荷较小时段，不同类型负荷的功率因数波动较小，因此，3种模型的补偿效果差异较小。

4 结 论

随着高比例电力电子设备广泛接入配电网，以及城市电缆化率的提升，用户无功用电发生明显变化。为了更好地进行无功优化配置，本文将负荷日功率因数曲线进行特征提取，并进行场景缩减，得到不同负荷无功用电组合场景集，然后综合考虑系统运行的经济性与安全性，建立了一种考虑负荷多无功用电场景的期望值无功补偿模型，通过修改后的IEEE 33节点系统进行仿真验证，得到如下结论：

1)根据大数据平台采集的信息，利用数据驱动，得到多用户日功率因数变化的组合场景集及其概率能直观反映新型城市配电网中负荷无功用电的不确定性，结合算例结果发现，此不确定性一方面体现在用户在不同时间里的功率因数差异较大，另一方面体现在配电网节点电压波动较大。

2)与传统优化模型相比，考虑负荷无功用电不确定性的无功优化配置能够更好地适应新型城市配电网运行的灵活性，防止电压越限，减小电压波动，保证系统运行稳定性。本文提出的考虑多无功用电场景的期望值优化模型可以在综合运行成本最低的条件下，最大程度保证系统电压水平，具备较好的经济性与灵活性。