基于SVD和双树复小波包的低速设备故障诊断
李洲统 张永杰
(1.绍兴天然气投资有限公司,浙江 绍兴 312075;2.北京讯腾智慧科技股份有限公司,北京 100029)
0 引言
低速重载设备是机械设备中最常见的设备,靠大齿圈与小齿轮啮合来传动的设备是低速重载设备中最典型的设备,齿轮副的运行状态直接影响整台设备的性能,因此,对这种低速重载设备的齿轮进行故障诊断具有非常重要的意义。
奇异值分解方法在信号降噪和周期成分提取方面具有优越性。但是对采集到的低速重载设备的信号来说,由于设备转速低,要想采集该信号的低频成分,保证较高的频率分辨率,就需要花费较长的采集时间,因此信号长度一般都很长,受计算机内存的限制,已无法用奇异值分解对这种信号进行降噪。
双树复小波变换是刚发展起来的一种新型的小波变换方法,其具有近似平移不变性、良好的方向选择性等特性,在图像处理、语音处理和故障诊断等领域已有相关应用。与传统小波包分解相比,双树复小波包分解的能量泄漏量更小,在该基础上进行后续包络分析,包络谱的特征更明显。
为了对低速重载设备进行故障诊断,该文有机融合了双树复小波包和奇异值分解方法,并将其成功应用于机械故障诊断。应用结果表明,该方法可以有效地提取低速重载设备的故障特征信息。
1 奇异值分解原理
奇异值分解(Singular Value Decomposition,SVD)是一种典型的正交化方法。对实矩阵∈R来说,不论其行、列是否相关,都存在一对正交矩阵(如公式(1)和公式(2)所示),使公式(3)~公式(5)成立。
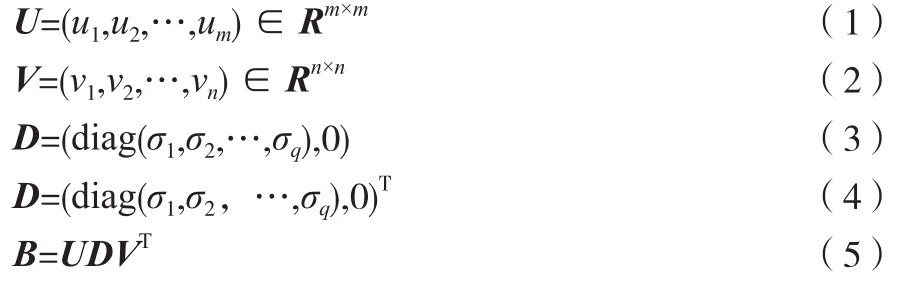
式中:和为一对正交的矩阵;u为矩阵中的列向量,每个列向量有个元素,个列向量u构成矩阵;R为行列的实矩阵;∈为集合中的属于;v为矩阵中的列向量,每个列向量有个元素,个列向量v构成矩阵;R为行列的实矩阵;为行列的实矩阵,即∈R;,,…,σ为元素 ;为特征值矩阵。
公式(3)或者其转置公式(4)主要取决于<还是>,∈,其中 diag(,,…,σ)为由元素,,…,σ构成的斜对角矩阵,=min(,),0为零矩阵,斜对角矩阵上的元素由大到小排列,即≥≥…≥σ≥0,这些元素称为矩阵的奇异值。
利用一维振动信号构造矩阵的方式有很多种,研究发现,构造Hankel矩阵更有利于信号的降噪。对离散信号=((1),(2),…,())来说,可以构造Hankel矩阵如公式(6)所示(1<<)。
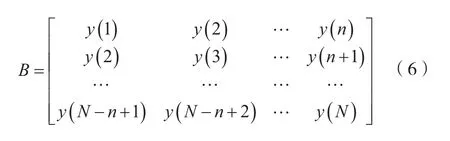
式中:为该矩阵不同的元素;括号中的数字为该元素在原始离散信号中的序列号,即这个在中是第几个数字。
令=-+1,则是一个行列的实矩阵,该矩阵被称为重构吸引子轨道矩阵,对该矩阵进行SVD分解,即可得到3个矩阵、和。
矩阵中的斜对角元素为奇异值,共有个元素,从大到小排列,依次为,,…,σ,下标数字表示该奇异值在奇异值序列中的位置,根据这个序列可以求得一个新的序列a,如公式(7)所示。
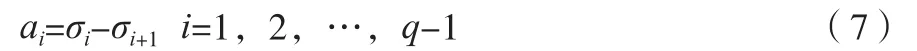
式中:σ为第个奇异值;为奇异值元素的下标(正整数),其取值为 1~-1。
按顺序将所有的a画出来,得到奇异值差分谱,如果相邻2个奇异值的差别较大,则在差分谱中产生1个峰值,在整个奇异值差分谱中必然存在1个最大的峰值a,这意味奇异值序列在处发生了最大突变,保留前个奇异值,其他奇异值置0,即可重构出1个新的信号,该信号包括原始信号中主要的频率成分。
奇异值分解是一种非常有效的信号降噪方法,在机电设备故障诊断中得到了广泛应用,但该方法存在一个明显的缺陷,即奇异值分解过程中涉及大量的矩阵运算,对计算机的内存有较高的要求,普通计算机处理长度为8 192的振动信号就已到极限,非常不利于低速重载设备的故障诊断,需要借助其他方法对低速重载设备振动信号进行降采样,同时又不能失去信号中的故障信息。
2 双树复小波包变换的基本原理
双树复小波包变换(DT-CWPT)的分解和重构过程如图1所示。其中,原始信号经过了2个并行的离散小波包变换,1个离散小波包变换为实部树,即图1虚直线的上半部,实部树中经过1个高通滤波器得到高频段的小波包分解系数,经过1个低通滤波器得到低频段的小波包系数,因此,该实部树将原始信号分解为2个不同的频段,到了第二层分解,又将高频段的小波包系数分解为高高频段和高低频段,将低频段的小波包系数分解为低高频段和低低频段,以此类推。图1虚直线下部为虚部树,采用另外1对高通滤波器和低通滤波器对信号进行分解。实部树和虚部树分解过程的区别如下:在进行第二层以上分解时,为了保证两树在该层和所有前层上产生的延迟差的总和相对原信号输入为1个采样周期,实树小波包分解交替使用Q_shift高通滤波器组,虚部树分解交替使用Q_shift低通滤波器组。
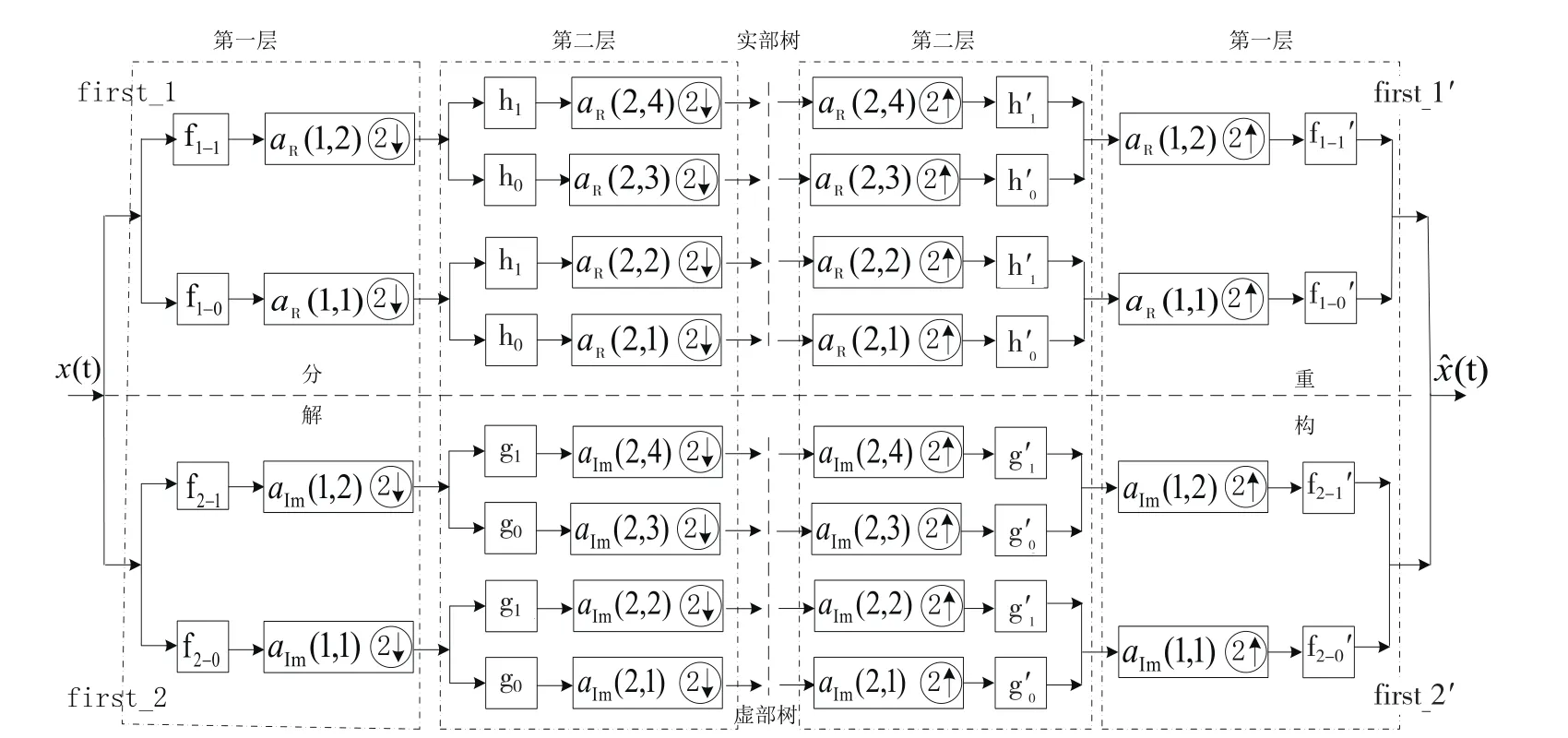
图1 双树复小波包变换的分解与重构过程
双数复小波包分解过程采用了系数二分法,去除了多余的计算,提高了分解效率,降低了信息的丢失率,且实部树和虚部树相结合的方式使双树复小波分解有更少的能量泄露,分解所得分量包括更少的理论频带范围外的干扰成分,更有利于后期的故障诊断。
在经过双数复小波包分解后,可以得到若干个不同频带的小波包分解系数,如果保留某个频带的小波包分解系数,将其他频带的小波包分解系数置0,然后再进行重构,就可以得到该频带范围内的振动信号,相当于对原始信号进行了一次带通滤波,但这种做法仍存在一定的局限性,即无法有效剔除该频带范围内的噪声,需要采用其他方法进行深度降噪。
与传统小波包分解一样,在双数复小波包分解过程中,每分解1次,数据量都会减半,分解层数越多,小波包分解系数的长度就会明显下降,从而给长数据的奇异值分解降噪带来可能性,利用奇异值分解对包括故障信息丰富的频带范围内的小波包系数进行降噪处理,然后再进行双数复小波包重构,可以极大地降低该频带范围内的噪声。
3 SVD和DT-CWPT诊断方法
为了实现低速重载设备的故障诊断功能,从而有效地去除低速重载设备振动信号中的强噪声,该文提出了有机融合奇异值分解和双数复小波包分解的诊断方法,步骤如下:1) 采集低速重载设备的振动信号,利用双树复小波包对该信号进行分解, 分解层数根据原始信号的长度来确定,要求分解得到的小波包系数的长度小于8 192。2) 选择包括故障信息最丰富的分量来构建Hankel矩阵,然后对该Hankel矩阵进行奇异值分解,在奇异值差分谱中找到最大的突变点,确定重构的奇异值个数,然后进行重构,实现信号的第一步重构。3) 对SVD重构的小波包系数进行双树复小波包重构,得到降噪之后的信号,再利用希尔包络解调方法得到该信号的包络谱,确定故障特征信息,识别故障类型。
4 工程应用
溢流型球磨机是金矿上的关键设备,一旦发生故障,将严重影响企业的正常生产。典型的溢流型球磨机结构如图2所示,球磨机一般有2个磨粉仓,矿石经进料口进入第一个磨仓,磨仓内装有很多不同大小的钢球充当研磨介质,驱动电机带动小齿轮,再驱动大齿轮旋转,大齿轮带着滚筒同步旋转,转动中产生一定的离心力,钢球在离心力的作用下到达一定的高度,又在自重力高于离心力后落下,撞击矿石,以达到研磨的目的,研磨到一定程度后再进入第二个磨仓进行细磨,磨成粉状物后通过卸料板排出,从而完成矿石的粉磨作业,为后续的冶炼黄金奠定基础。
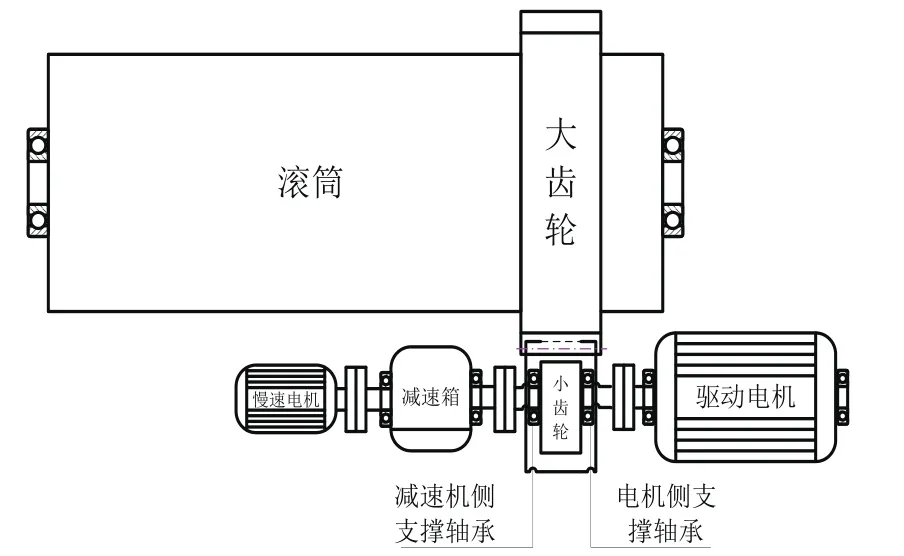
图2 溢流型球磨机结构示意图
某金矿1台球磨机发生较大的振动,技术人员采集了该球磨机的振动信号,测量位置为小齿轮两端、减速机侧支撑轴承以及电机侧支撑轴承。大齿轮转频即滚筒转频为0.240 Hz,小齿轮转频为3.333 Hz。由于信号长度超过8 192,传统的奇异值分解方法已不再适用,因此利用该文所提出的方法对该信号进行分析,从而对球磨机进行故障诊断分析,故障诊断中所用的数据见表1。
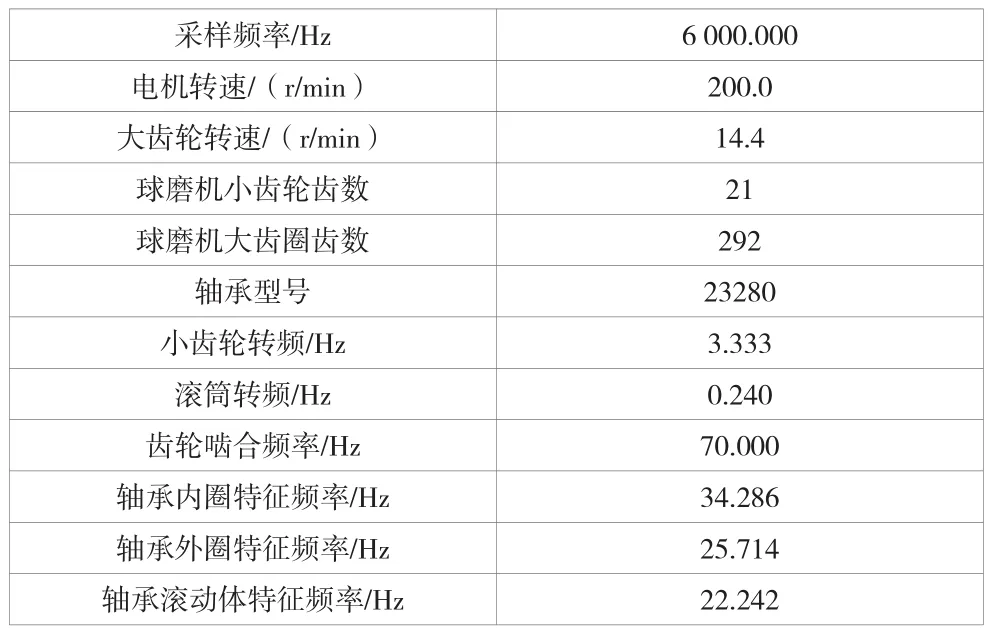
表1 相关参数
采集到的振动信号如图3所示,时域波形比较杂乱,看不出任何故障信息,频谱图中存在明显的啮合频率(70.040 Hz)及其倍频(140.000 Hz、210.100 Hz和280.000 Hz),啮合频率是齿轮运转过程中经常出现的频率成分,无法据此识别故障齿轮对应的特征频率。
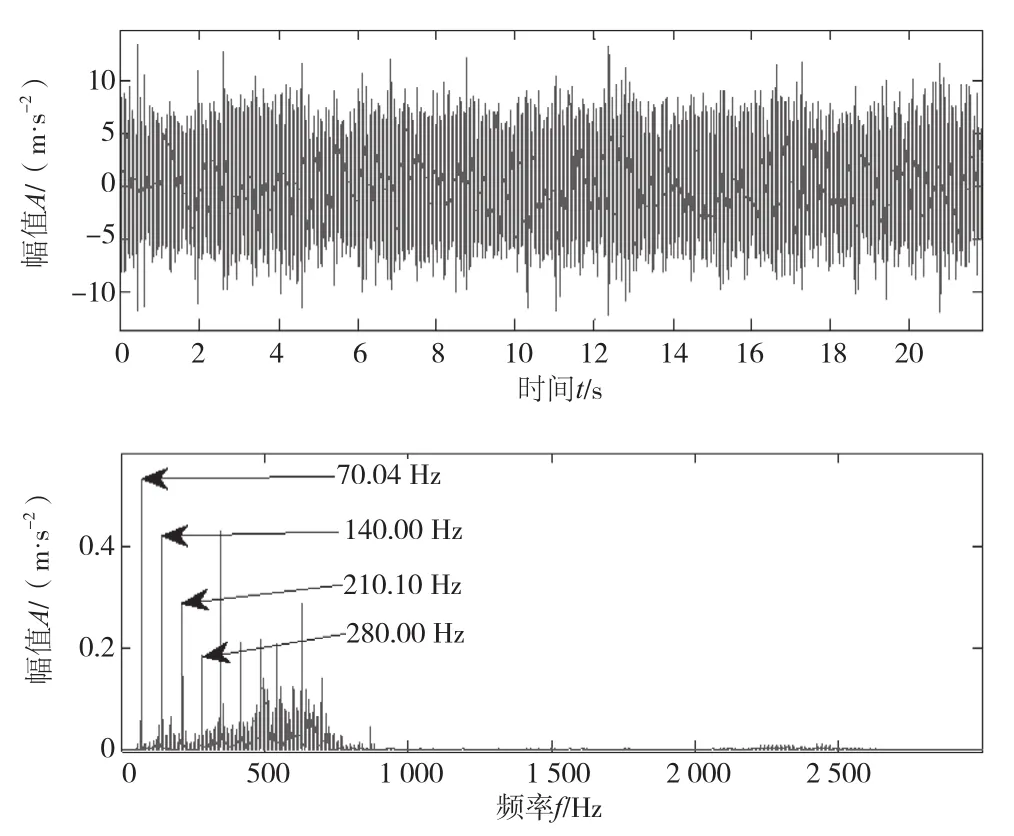
图3 原始信号的波形图和频谱图
由于信号的长度为131 072,因此无法直接进行奇异值分解,必须把数据长度降到8 192以内,利用该文提出的方法对该信号进行4层双树复小波分解,每个频带的点数为8 192。
因为啮合频率70.040 Hz附近的冲击比较大,所以对包括70.040 Hz的频带(即第一个频带)的小波系数进行奇异值分解,实部和虚部的奇异差分谱如图4所示,实部和虚部都在第四点出现了较大突变,对实部和虚部奇异值分解的前4个分量进行奇异值重构,从而对第一个频带的小波系数进行降噪,双树复小波重构后的信号如图5所示,时域波形中出现明显的周期性冲击,周期大约为4.368 s,对应的频率为0.228 94 Hz,与表1中的大齿轮故障特征频率非常接近,啮合频率70.040 Hz局部放大图如图6所示,出现了边频70.270 Hz,边频带宽为0.230 Hz,与大齿轮的转频0.240 Hz非常接近。
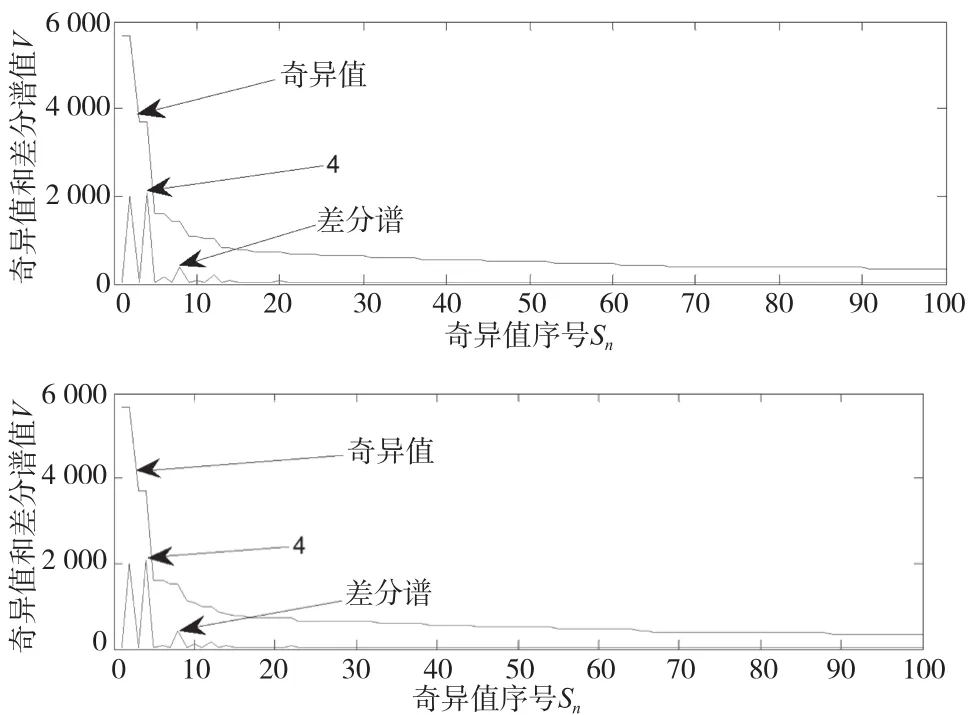
图4 奇异值和差分谱前100个点
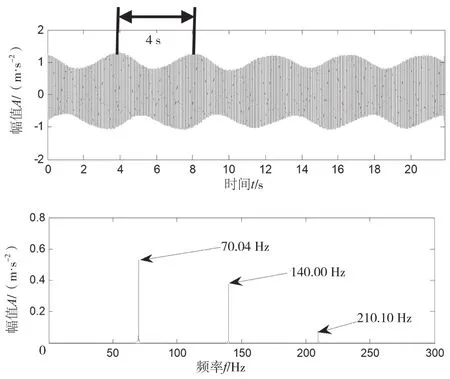
图5 重构后信号的波形和频谱
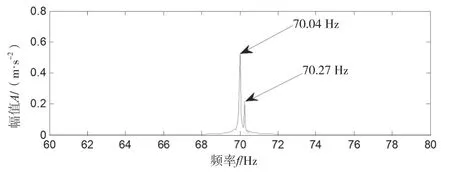
图6 频谱局部放大图
重构信号的包络谱如图7所示,包络谱中存在2个明显的峰值(0.228 9 Hz和0.457 8 Hz),与大齿轮的转频和二倍频非常接近,因此可以断定大齿轮发生了故障,后来该厂工作人员对球磨机进行检查,发现大齿轮出现了磨损故障,与利用该文所提出的方法的诊断结果相吻合。
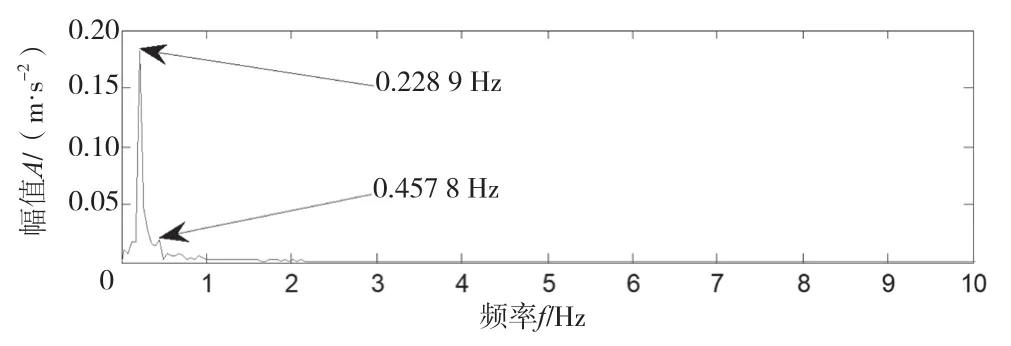
图7 重构后信号的希尔伯特包络谱
5 结语
该文研究了将奇异值分解与双树复小波包分解结合的方法,通过仿真实例和工程应用验证了该方法的有效性,得出的结论如下:1) 双树复小波包可以将振动信号分解为多个不同频段的分量,从而有效去除一些干扰成分。2) 奇异值分解可以保留信号中绝大部分有用成分,同时又最大限度地消除噪声。3) 将2种方法有机融合并应用于低速重载设备的故障诊断可以有效地找到故障特征信息,从而达到识别故障模式的目的。

