次分数布朗运动机制下具有浮动敲定价格的亚式期权定价
王竟莘,王欣怡,郭志东
(安庆师范大学数理学院,安徽 安庆 246133)
0 引言
期权定价一直是金融数学领域的热点问题.自经典定价模型Black-Scholes模型被BLACK和SCHOLES[1]提出以来,研究者们通常用几何布朗运动和分数布朗运动作为驱动源驱动标的资产价格,取得了大量研究成果.韩利华等[2]基于几何分数布朗运动,利用保险精算方法求得亚式期权定价公式.于文明等[3]建立混合分数布朗运动和不变方差弹性的亚式期权定价模型,利用渐进展开方法给出了期权定价公式,对赫斯特指数和渐进逼近值进行数值分析.陈聪等[4]给出了在几何布朗运动下的算数平均半亚式期权定价的近似半解析法,进一步利用对偶变量技术减少该方法的计算时间.KAHALÉ[5]运用多层次蒙特卡洛方法计算到期日的亚式期权价格,并将此方法与Milstein格式(由标量随机微分方程驱动的过程)、Euler格式(由多维随机微分方程驱动的过程)相结合,数值结果表明该方法优于传统的蒙特卡洛算法.LU等[6]研究了基于不确定理论的亚式期权定价问题,利用期望值和乐观值给出了亚式期权的定价公式,通过数值实验验证了结果的有效性.王伟[7]建立分数布朗运动下的亚式期权定价模型,利用无套利原理,经过Markov调制求得具有固定敲定价格的亚式看涨和看跌期权定价公式.沈明轩[8]建立了混合分数布朗运动下的幂型几何平均亚式期权定价模型,利用拟条件期望给出其定价公式并推广到支付红利情况下.ZHANG[9]建立了分数布朗运动下带有交易费和支付红利的亚式期权定价模型,利用无套利原理和分数公式,给出了几何亚式期权的定价公式和看涨-看跌平价公式,通过数值计算讨论赫斯特指数和到期日对期权价格的影响.
2004年,BOJDECKI等[10]提出次分数布朗运动,相较分数布朗运动,次分数布朗运动具有协方差随时间的增加而迅速衰减、增量在非重叠区间内的相关性较弱、同样具备相似性和长程相关性的特点,因此次分数布朗运动更适合应用于金融市场.许多学者进行了相关研究,程潘红等[11]建立了该环境下支付连续红利的可分离交易可转债定价模型,利用Mellin变换得到了显示公式,通过数值模拟分析交易可转债价格随参数变化的趋势.梁喜珠等[12]利用随机分析理论和保险精算方法,建立该环境下的最值期权定价模型并求得定价公式,通过数值计算对市场不同的分形结构对期权价格的影响进行分析.刘晓敏[13]建立了单资产多噪声的最优投资组合模型,利用随机分析理论给出了次分数布朗运动下最优投资组合的显示公式.然而,上述研究并未探讨次分数布朗运动机制下具有浮动敲定价格的几何亚式期权定价问题,本文将对该问题进行研究.
1 次分数布朗运动和亚式期权

(i)自相似性:当a>0时,有{ξH(at),t≥0}{aHξH(t),t≥0};

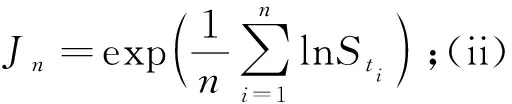
2 次分数布朗运动机制下具有浮动敲定价格的亚式期权定价
基于偏微分方法,讨论次分数布朗运动下具有浮动敲定价格的几何平均亚式期权定价问题.考虑Black-Scholes模型的次分数形态,即简单金融市场模型下,其标的资产价格St满足:
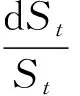
(1)
引理2.1[15]若函数f(t,ξH(t))为一个二元微分,则次分数布朗运动有It公式:
(2)
证明
定理2.1 假设标的资产价格St符合(1)给出的模型,则该亚式期权的V(t,S,J)价格满足偏微分方程
(3)
且终值条件满足:
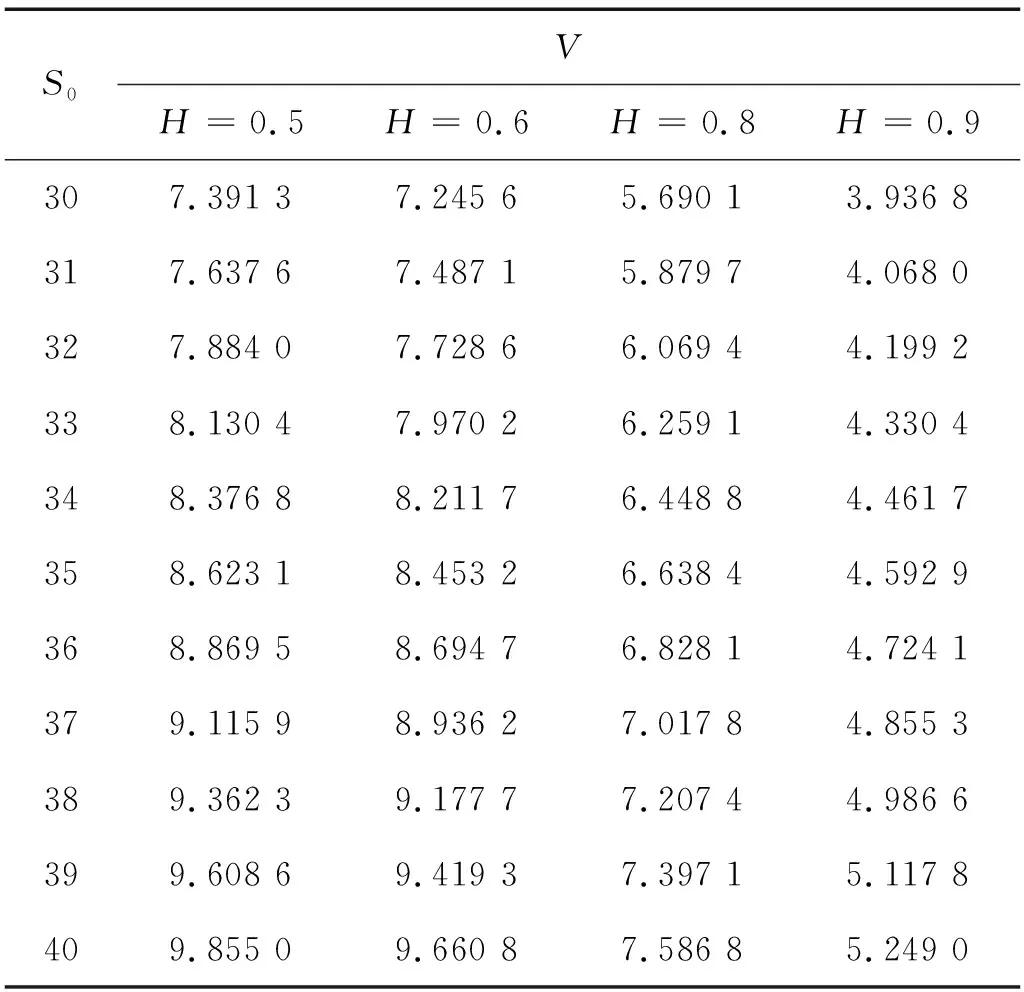
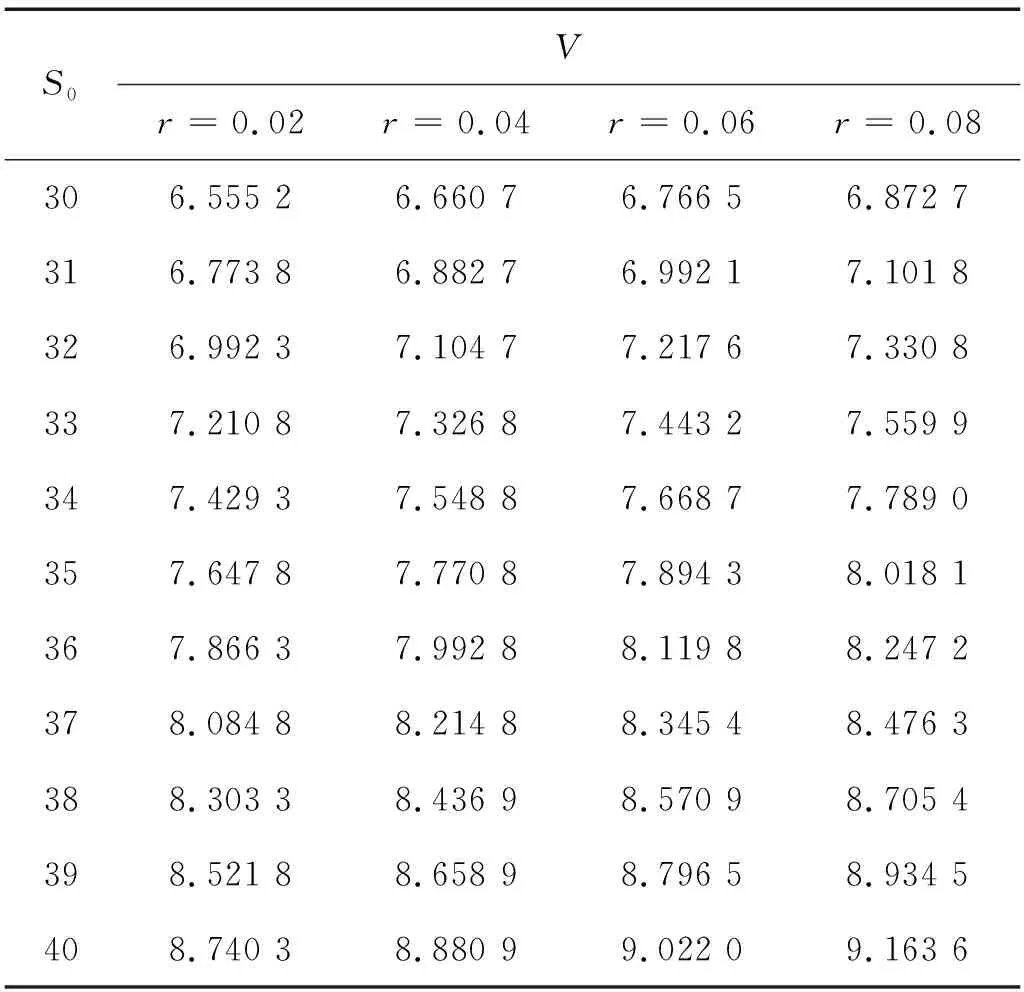
V(T,S,J)=(S-J)+,0 (4) 证明 考虑一个复制的投资组合Π包含一份期权Vt(t,St,Jt)和Δ份股票.在t时刻这个投资组合的价值为Π=V-ΔS. 假设Δ在时间区间(t,t+Δt)内没有变化,则我们选择合适的Δ,使Π在时间区间(t,t+dt)内无风险. dΠ=dV-ΔdS= (5) dΠ=rΠdt=r(V-ΔS)dt, 可得 (6) (7) 替换(7)到(6)中,可得 (8) 则定理2.1得证. 若求解偏微分方程(3)和终值条件(4),可得如下定理. 定理2.2 若标的资产价格St遵循(1),则该亚式期权的Vf(t,S,J)价格为 (9) 其中,函数Φ(x)是标准正态分布的累积概率函数,J为路径变量,且 证明 令 x=lnS, (10) V=U(x,y,t). 有偏微分: (11) 将(11)带入(3)(4),可得 (12) U(T)=(ex-ey)U0(x,y). (13) (14) (15) 求解微分方程(14)(15),得到 (16) 其中, h4=r(T-t)-h1, h6=r(T-t), 利用傅里叶逆变换,可得 (17) 其中, U0(μ,k)=(eμ-ek)+, (18) 最终由公式(10)(17)(18),定理2.2得证. 定理2.3 几何平均亚式期权看涨-看跌平价关系式为 C(S,J,t)-P(S,J,t)= 证明 令 W(S,J,t)=C(S,J,t)-P(S,J,t), 在{0≤S<∞,0≤J<∞,0≤t≤T}上,W满足: (19) 考虑Cauchy问题: (20) (21) W(x,y)=a(t)ex-b(t)ey. (22) 带入(20)(21),经比较系数得 (23) 且有 (24) 求解(23)(24),得到 (25) 将(25)代入(22),并考虑(10),定理2.3得证. 基于次分数布朗运动模型,以具有浮动敲定价格的亚式期权为例,用数值模拟计算探究Hurst指数H对期权价格的影响. 已知t=0时,有几何平均亚式看涨期权Vf(0,S,J). Vf(0,S,J)=S0Φ(-d1)-S0exp(ρ1-ρ2)Φ(-d2). 假设模型相应参数为T=0.5,r=0.05,σ=0.8,Hurst指数H分别为0.5、0.6、0.8、0.9时,次分数布朗运动下,具有浮动敲定价格的几何平均亚式看涨期权的计算结果如表1所示,比较图如图1所示. 表1 r=0.05,H取不同值时几何平均亚式看涨期权计算结果 图1 H取不同值时几何平均亚式看涨期权计算结果比较 T=0.5,H=0.7,σ=0.8,无风险利率r分别为0.02、0.04、0.06、0.08时,次分数布朗运动下,具有浮动敲定价格的几何平均亚式看涨期权的计算结果如表2所示,比较图如图2所示. 图2 r取不同值时几何平均亚式看涨期权计算结果比较 表2 H=0.7, r取不同值时几何平均亚式看涨期权计算结果 由表1和图1可知,H固定时,随着股票价格S0增加,期权价格V逐渐增加;S0固定时,随着H增加,期权价格V逐渐减小. 由表2和图2可知,r固定时,随着股票价格S0增加,期权价格V逐渐增加;S0固定时,随着r增加,期权价格V也逐渐增加. 比较图1和图2可发现,从整体趋势来看,期权价格V受Hurst指数H的影响相对来说较大,受无风险利率r的影响相对来说较小. 求得期权的显示表达式是研究期权定价问题非常重要的一步.本文运用傅里叶变换方法给出了具有浮动敲定价格的几何平均亚式期权显示表达式,进而探究了次分数布朗运动机制下具有浮动敲定价格的几何平均亚式期权定价问题.通过数值计算结果发现,Hurst指数和无风险利率固定时,股票初始价格与该期权价格呈正比;股票初始价格固定时,Hurst指数与该期权价格呈反比,无风险利率与该期权价格呈正比.
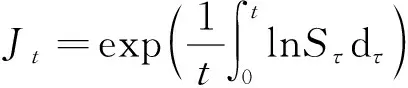
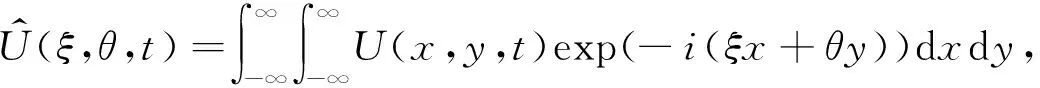
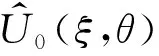


3 数值计算


4 结语

