基于腐蚀损伤和裂纹损伤的金属结构疲劳寿命研究
徐罗军 徐 超 邓代军 黄罗飞 张丛敏
湖北特种设备检验检测研究院宜昌分院 宜昌 443000
0 引言
起重机械中多数机械零部件所承受的工作载荷是交变载荷。结构零部件在交变载荷作用下,某些高应力或存在缺陷的部位会发生损伤并逐步积累,致使功能退化,表现为裂纹萌生、扩展直到彻底断裂的失效形式,使用频率越高起重机械的金属结构越容易发生疲劳破坏[1]。
起重机械的失效可由一种或多种过程引起,其失效形式可以是单一的过程现象,也可以是组合的过程现象,其结果是一个宏观现象的表征。如腐蚀一般被认为是单一的过程,过程表征是构件表面受到腐蚀损伤;疲劳一般也被认为是单一的过程,由周期变动载荷引起构件的机械损伤,过程表征是构件中疲劳裂纹的萌生、扩展以至断裂。腐蚀或疲劳各是独立的一种失效形式,而腐蚀疲劳则可认为是组合的过程现象,由于其出现的普遍性、后果的严重性,且腐蚀与疲劳互相增强,往往不作为是2 个单一失效形式的同时出现,而是两者组合由协同效应引起的一种失效形式。在腐蚀疲劳失效中,活性腐蚀的存在会加剧疲劳,而周期变动的疲劳载荷的存在又加剧了腐蚀,腐蚀疲劳已被作为一种独立的失效形式。
起重机械的有效工作年限主要取决于其金属结构不发生疲劳破坏[2,3],对起重机械金属结构的疲劳寿命研究我国有许多学者专家进行过研究,徐格宁等[4]利用Paris 公式和Miner 线性累积损失理论推导了桥式起重机焊接箱型主梁的疲劳剩余寿命公式,并开发了剩余寿命预估系统;程文明等[5]在断裂力学基础上运用时间循环法,通过仿真计算金属结构裂纹的疲劳裂纹扩展寿命;杨先勇等[6]将现场测试结果与有限元计算结合编制载荷谱,并应用修正Miner 法则、修正后的P-S-N 曲线和Corten-Dolan 非线性损失理论对起重机在变幅载荷下的疲劳裂纹扩展寿命进行了分析;张川等[7]采用分形维数法考虑闸门锈蚀特性,并构建了基于分形维数预测金属剩余寿命的完整体系;张福泽[8]提出了D-H 曲线预测金属任意腐蚀损伤推算日历寿命模型。现有通常所采用的起重机械金属结构疲劳寿命计算过程中,将材料腐蚀损伤因子和焊缝裂纹损伤因子两者独立考虑,未将两者的协同损伤过程同时考虑,故在进行寿命预测过程中与实际情况存在较大的偏差。
在对起重机械金属结构疲劳寿命评估计算过程中,同时考虑了材料腐蚀损失和焊缝裂纹损伤,分别求出钢结构的腐蚀、焊缝这2 个因素对钢结构屈服强度的损伤因子,最终求出材料随着时间老化后的屈服极限,利用这几个因素来建立一个钢结构屈服特性随时间变化的模型,从而得出钢结构比较可靠的屈服强度极限,并利用疲劳累积损伤假说理论计算金属结构疲劳寿命,使计算结果更加符合实际和准确。
1 疲劳寿命评估原理
考虑到机器随着服役时间的增长,其材料的屈服极限会因为工况、环境因素等有所下降,所采用的寿命研究思路是分别求出钢结构的腐蚀、焊缝这2 个因素对钢结构的屈服强度的损伤因子K2、K3,最终求出材料随着时间老化后的屈服极限,利用不做试验求金属结构疲劳强度的理论公式验证求得的屈服强度,采用累积损伤理论计算实际工况下不同情况的最大等效应力值对应的寿命,最后结合疲劳累积损伤假说公式计算出最终的剩余寿命。
1.1 材料随时间老化后的屈服极限模型建立
考虑到机器随着服役时间的增长,其材料的屈服极限会因为工况、环境因素等有所下降,分别求出钢结构的腐蚀、焊缝这2 个因素对钢结构屈服强度的损伤因子K2、K3,求出材料随时间老化后的屈服极限σst为

由式(1)中的因素建立一个钢结构屈服特性随时间变化的模型,可得出钢结构比较可靠的屈服强度极限。绘制出考虑损伤因子的钢结构S-N 曲线后,并将应力循环(应力水平、应力循环次数可认为在各个年份基本不变)也放入该S-N 曲线图中,则两者必定会在某处有一个交点,而这个交点即为预测的剩余使用寿命值。
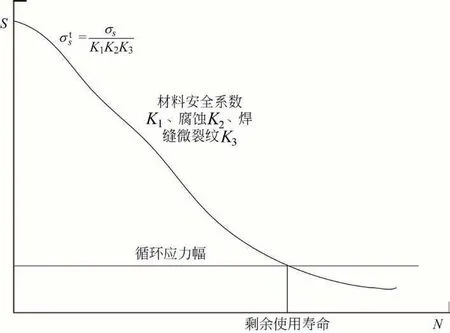
图1 考虑损伤系数的S-N 曲线
1.2 安全系数K1 的确定
依据GB/T 3811—2008《起重机设计规范》[9]无风工作情况、有风工作情况、受到特殊载荷的工作或非工作情况3 种不同情况,确定金属结构安全系数K1。如表1 所示,A 为无风工作情况,B 为有风工作情况,C 为受到特殊载荷的工作情况或非工作情况。
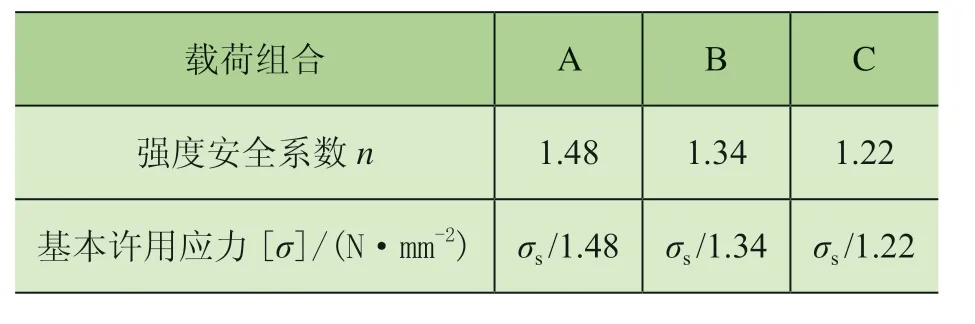
表1 安全系数K1 和钢材的基本许用应力[σ]
1.3 腐蚀对屈服强度的损伤因子
文献[8]给出了腐蚀损失容限和金属日历寿命的函数关系,提出将金属的腐蚀容限设置成一个变量处理,并推导出金属腐蚀试验日历寿命为
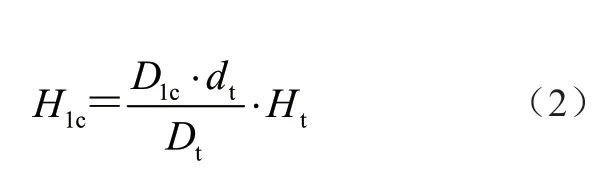
式中:D1c为正常使用情况下的湿度、温度、腐蚀溶液浓度对应的腐蚀损伤容限值,H1c为与D1c对应的正常使用寿命,dt为腐蚀试验溶液浓度,Dt为腐蚀损伤,Ht为试验历时。
文献[10]对式(2)进行变形,得腐蚀系数k 为
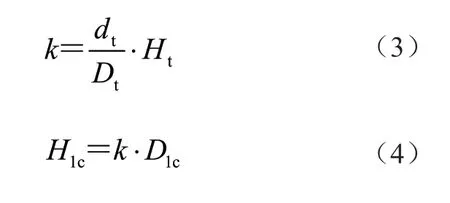
李伟康等[10]通过金属加速腐蚀实验得到了Q235 钢材的屈服强度指标,对公式的正确性进行了验证,并确认了k 为一常数,近似等于46.58。同时对Q235 钢材不同失重率下的实际屈服强度进行最小二乘法线性回归,得到其屈服强度与失重率退化的关系,如图2 所示。

图2 锈蚀钢材屈服强度比与失重率关系
其拟合曲线函数式为
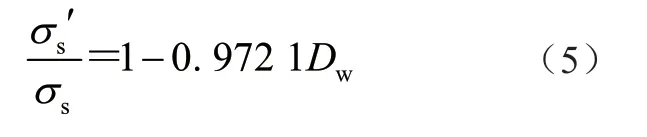
式中:Dw为失重率,σs'为锈蚀后的屈服强度,σs为钢材原屈服强度。
近似认为Q235 的蚀余屈服强度模型也能适用于Q345,通过式(5)分别计算出Q345 在失重率为6%、7%、8%、9%、10%的锈蚀后的屈服强度为324.88 MPa、321.52 MPa、318.17 MPa、314.82 MPa、311.46 MPa。由于该实验对应不同失重率的时间是在实验室的加速腐蚀试验条件下进行的,所以在自然状态下达到相应的失重率的时间应该更长,而水工门式启闭机经常做锈蚀防护,故这个时间被延长。
分别对厚度6 mm、9 mm、14 mm 的失重率与实验时间进行线性拟合得出的函数为
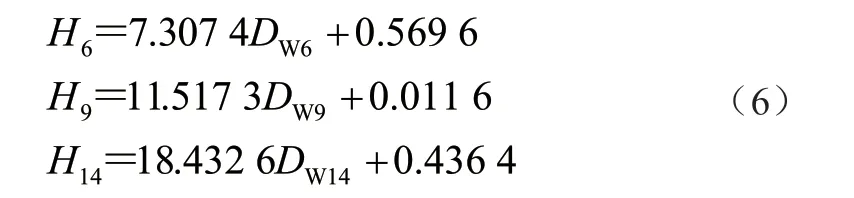
式中:H6为厚度6 mm 钢材的实验时间,DW6为厚度6 mm钢材的失重率,H9为厚度9 mm钢材的实验时间,DW9为厚度9 mm 钢材的失重率,H14为厚度14 mm 钢材的实验时间,DW14为厚度14 mm 钢材的失重率。
在对其进行统一得到一般厚度下腐蚀时间与失重率的数学模型为

式中:H 为钢材的实验时间。
式(7)可计算出腐蚀到6%的失重率时所花的时间为74.85 d(室外加速腐蚀时间),最终需要根据起重机在有防护条件下得出腐蚀失重率与实际时间的关系,则需要引入修正系数K2、常数项M,得出的函数式为

由于没有文献给出该加速实验相较于自然时间的函数关系,故无法得出式(8)中的修正系数K2。而式(8)求出的时间单位为天,若将其转化为年时,上式的常数项M 可忽略不计。所以,当腐蚀时间单位为年时,腐蚀时间与腐蚀率成正比例关系。

由此,得出其失重率与实际时间的函数关系为
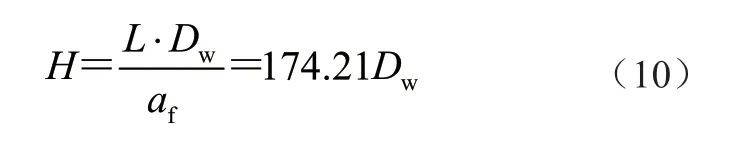
式中:af为材料的腐蚀速率;L 为材料的初始厚度,此处考虑现场结构钢板厚度,取值为10 mm。
结合式(5)、式(10)得出各腐蚀率下的材料屈服强度的腐蚀损伤因子,如表2 所示。

表2 腐蚀损伤因子
1.4 焊缝裂纹对屈服强度的损伤因子
门架作为起重机械典型的焊接结构,由于焊接部位存在着如焊接残余应力等焊接缺陷,在使用过程中,结构断焊、焊缝开裂以及断裂等现象时常发生。焊接主梁是门架的主要结构件,交变载荷是其主要载荷特征,疲劳失效是其主要失效形式,故有必要对焊接主梁疲劳裂纹扩展的机理进行分析。焊缝许用应力如表3 所示。

表3 GB/3811—2008 焊缝的许用应力
在文献[12]中,初始裂纹长度a0=0.5 mm,临界裂纹长度ac=100 mm,由表4 可知当裂纹扩展长度达到临界裂纹长度时,焊接主梁的疲劳寿命约为 27.17 a。
由表4[12]可知,当裂纹长度小于16 mm 时,裂纹扩展的速度缓慢,此阶段焊接主梁趋于安全;当裂纹长度超过16 mm 时,裂纹扩展的速度呈陡增趋势,故此阶段焊接主梁趋于危险。当门式启闭机使用超过24 a 时,应对门式启闭机给予高度重视,及时维修或更换危险部件。
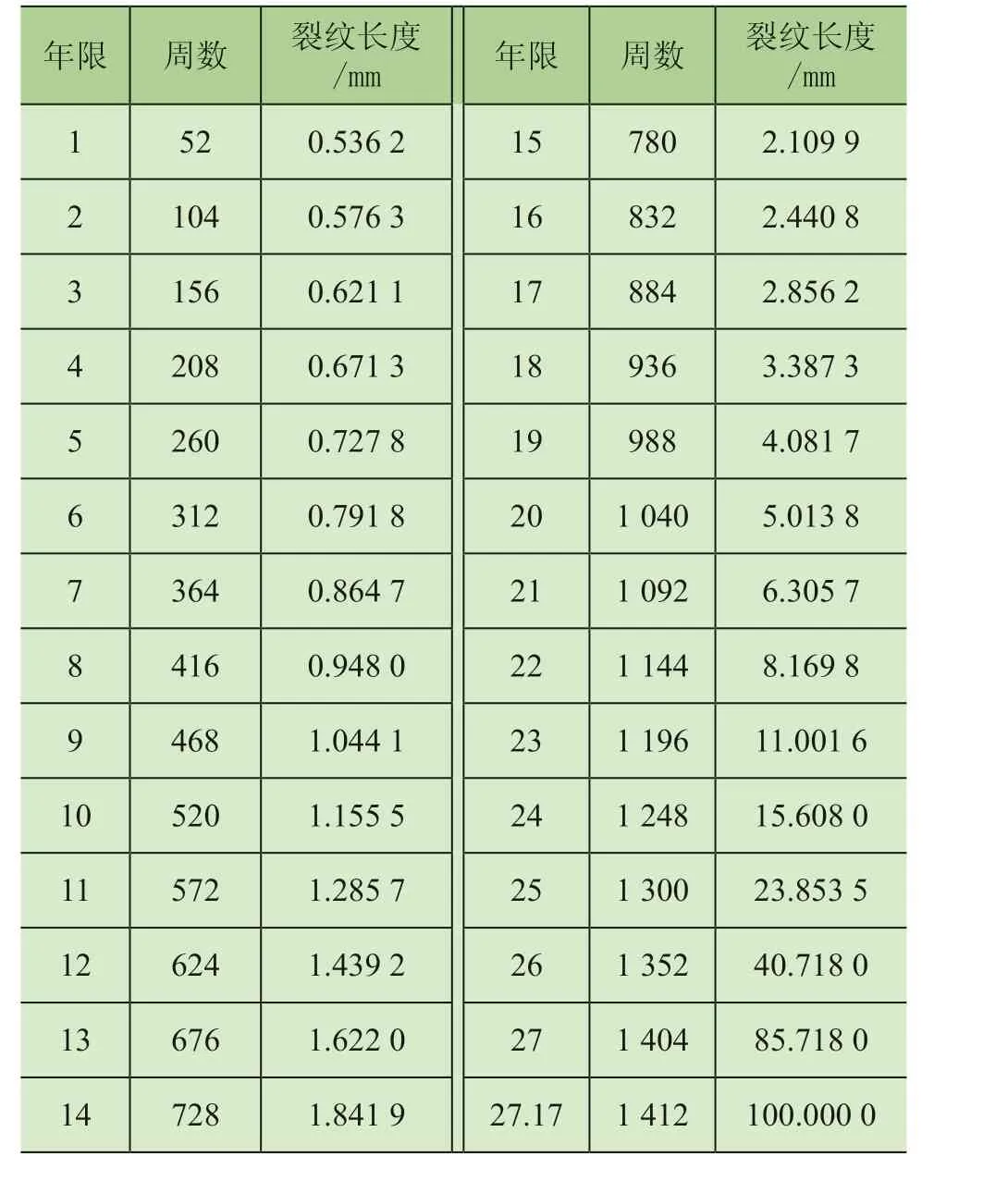
表4 焊接主梁裂纹扩展
由上述可知,当主要受力构件上的裂纹长度达到该部位允许的最大裂纹长度(临界裂纹长度)的16%时,应对此给予高度重视并及时进行维修。
在课堂上我们利用微课小视频进行教学,在课后我们仍旧可以利用微课让学生巩固课堂知识。课堂的时间是有限的,我们在抓住课堂时间进行教学时,也需要让学生科学合理地利用课后时间,因为课后学习很多时候没有教师请教也没有同学讨论,这时候微课的价值就得到了充分的体现,学生可以根据自己的实际学习情况选择微课学习,在微课堂中讨论学习内容等。另外我们鼓励学生运用微课的同时,我们自己也要善于利用微课,让微课更好地服务学生、服务数学课堂。我们在教学过程当中可以通过微课不断学习优秀教师的教学方法,使其内化到自己的教学体系当中,从而更好地传授学生知识、引导学生学习,这样才能使课堂质效有更好的提升。
在文献[12]中,针对无限长裂纹,推导计算出与S-N曲线对应的含无限长裂纹结构质量等级,确定了不同质量等级下无限长裂纹的允许深度,根据文献[13]中的图9 可以得出结果如表5 所示。

表5 工件厚度对应的最大裂纹深度
根据对现场门式启闭机主要结构件的焊缝进行的超声检测结果,在焊缝超声检测报告中,检件的厚度L =10 mm,其中在0 ~800 mm 和0 ~1 200 mm 这2 处有缺陷,其长度分别为800 mm、1 200 mm;深度缺陷分别为8 mm、9 mm,显然处于不合格等级内。目前尚未有裂纹与剩余强度关系的实验数据,于是结合表1 和表3 选择正常的无风工作情况,即A 载荷工况与D 等级应力情况来求出焊缝在焊缝缺陷达到临界状态时的强度损伤系数K3。

又根据焊缝裂纹的超声波检测中35 个测点只有3个不合格,对K3' 引入修正系数f,其中f =1-3/35。最终求得焊缝裂纹损伤系数K3= f·K3'=1.62。
2 疲劳极限及循环基数
2.1 疲劳极限及循环基数的确定
考虑腐蚀和焊缝裂纹后的剩余屈服强度为

根据式(12)求出材料的最终剩余强度,考虑材料加工成零件时会有一定的损伤,故最终的门机主梁剩余屈服强度σst =100 ~130 MPa。查找材料的屈服特性为100 ~130 MPa 的材料试件的S-N 寿命试验数据,从中找出对应的对称循环应力σ-1下的试验寿命N0。结合在现场测试的5 种应力状态对应的工况下,并考虑小车4 对轮组的质量为42 t,小车钢结构的质量为32 t 之后的最大等效应力值分别为(载荷15 t)181 MPa、(载荷45 t)192.62 MPa、(载荷87.3 t)209.6 MPa、(载荷75 t)204.66 MPa 和(载荷145.5 t)232.67 MPa,其年均循环次数分别为163 次、106 次、106 次、57 次、57 次,算出目前已经服役34 a 的工作时间所有工况的应力循环次数。
根据铸铁类别、铸件的壁厚以及其力学性能的对应关系,假设剩余拉伸强度接近HT250 ~HT300,考虑到机构尺寸越大其强度越小,且从材料到零件有一定的损伤,故可取剩余拉伸强度σbt=270 MPa。
又根据《机械设计手册》[14]可知Q 系列钢材其抗拉强度为355 ~600 MPa(见表6),由于本文计算出来的剩余屈服强度明显要小于一般的钢材,但材料与灰铸铁的性能不太相同,本文按照大尺寸零件的抗拉强度的线性变化对其进行拟合,相应的拟合曲线如图3所示。

图3 σb 与σs 的线性拟合
表6 C 钢抗拉强度线性取值
得出的函数关系式为

式中:σb为试件的抗拉强度,σs为材料的屈服强度。
根据拟和关系求得σb=245 MPa,这与根据工况参考HT250 ~HT300 比较一致,本文根据文献[15]不做试验求其疲劳强度的理论计算方法

式中:σ-1为试件的试验疲劳强度,E 为钢的弹性模量。
由文献[16]可知,在弯曲疲劳和拉伸疲劳时,中等尺寸零件取m =9、应力循环基数N0'=5h 106;大尺寸零件受弯曲疲劳时m =9,N0'=5h 107。考虑到门式启闭机已经服役34 a,此处本文取最小值,取m =9,N0'=5h 106。又根据文献[14]计算疲劳试验的循环基数公式
式中:N0为试件的疲劳试验的循环基数,取N0=5.26h 106。
2.2 疲劳极限及循环基数的理论值检验
由《机械设计》[16]可知,经过调制后的45 号钢的抗拉强度σb>600 MPa,屈服极限σs为355 MPa,其某一项的弯曲疲劳试验中的相关性能数据:σ-1=301 MPa,m =9,N0=5h 106。该钢材经过调制处理,故可取抗拉强度650 MPa。按照理论计算,得出其σ-1=309 MPa,取m =9 和循环基数N0=4.8h 106。σ-1与实际结果基本一致,只是循环基数可能存在较小偏差,故可按照上述的理论方法进行计算。
3 考虑损伤系数的疲劳寿命计算的案例实施
案例选取某电站坝顶门式启闭机,其主要金属结构为Q345,屈服强度为345 MPa。通过对其主要金属结构进行基于腐蚀损伤因子和焊缝裂纹损伤因子累计损伤计算,确定其剩余疲劳寿命。首先利用Ansys 对门式启闭机进行三维建模仿真,结合实际情况进行有限元分析,明确在主梁中部为应力集中危险部分。然后现场贴片,进行实际吊载动态应力测试,测得不同工况下的等效应力值。最后建立金属结构剩余疲劳强度模型,查出结构的安全系数,计算出腐蚀损伤系数和焊缝裂纹损伤系数,并利用模型计算出结构剩余疲劳强度。
零 件 的 性 能 为σ-1=116 MPa,m =9,N0=5.26h 106。对试件进行试验,以对称循环变应力σ1=181 MPa 作用5 542 次,σ2=192.62 MPa 作用3 604 次、σ3=209.6 MPa 作用3 604 次,σ4=204.66 MPa 作用1 938 次和σ5=232.67 MPa 作用1 938 次,以后使用过程中选择以σ6=204.66 MPa 作用于试件。
利用不做试验求其疲劳强度的理论得
利用计算疲劳试验的循环基数公式得
式中:m、c 均为常数,N 为应力循环基数,σi为第i 种情况下的对称循环变应力。
分别求出5 种工况下的循环寿命为

根据疲劳累积损伤假说有

式中:Ni为第i 种工况下的循环寿命,ni为第i 种工况下的工作周期数。
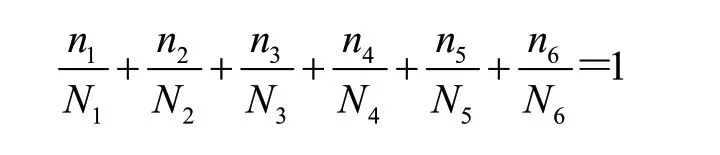
求得n6/N6=0.481。
按照工况4,每年工作365 次,n6=0.481 N6=15 274.113 次,则15 274.113/365 =42,即该门式启闭机还能工作42 a。
4 结论
1)金属结构的腐蚀与疲劳是互相增强,往往不作为是2 个单一失效形式的同时出现,而是两者组合有协同效应引起的一种失效形式。
2)考虑到起重机械金属结构在实际使用中受到腐蚀和焊缝裂纹损伤双重因素的影响,引入材料腐蚀损伤因子和焊缝裂纹损伤因子,建立材料剩余屈服强度模型,并对其进行计算,解决一直以来计算金属结构疲劳寿命只考虑某单一因素引起的误差,使计算结果更加符合实际和准确。
3)对某大坝已服役34 a 的门式启闭机进行应力检测、虚拟仿真,在计算出材料腐蚀损伤因子和焊缝裂纹损伤因子前提下,根据疲劳累积损伤假说理论计算出门式启闭机的金属结构的剩余疲劳寿命为42 a,计算结论与实际结果拟合程度较好。

