考虑原产地规则的跨境纺织供应链网络设计
茅 茂, 王长军
(东华大学 旭日工商管理学院, 上海 200051)
近年来,一方面,经济的全球化趋势促使包括纺织企业在内的中国制造企业展开跨境布局,以获得原料、生产及市场等要素的全球配置;另一方面,随着国内劳动力等各项成本的不断攀升,也促使制造企业“走出去”。在如上的外部和内部因素驱动下,我国纺织企业的供应链网络全球化也已成为趋势[1],但是,跨境布局的企业却面临着贸易制度安排带来的挑战和机遇。在阻碍跨境贸易的众多制度中,原产地规则是需要被重点关注的一项[2],它会造成跨境贸易中关税差别对待,这迫使企业为规避贸易管制措施,改变自身的供应链安排[3],从而,在一定程度上改变了全球供应链的布局。注意到这样的贸易管制措施会对全球供应链造成的复杂影响,经济联系紧密的国家会考虑联合起来,通过达成大型区域贸易协定,以新的制度安排,以规范贸易障碍对全球供应链利益实现带来的干扰[4]。其中,最具有代表性的就是2020年底签署的《区域全面经济伙伴关系协定》(RCEP协定)[5]。该协定由东盟发起,中、日、韩、澳及新西兰等15个国家签署加入。为减少域内企业的贸易壁垒,RCEP协定中最重要的突破之一便是制定更为灵活自由的区域累积原产地规则,即产品增值部分只要属于成员国,且累积增值超过40%,便可视为原产地产品,享有关税免除。而考虑到协定实施后可覆盖全球近一半人口和近三分之一的贸易量,相关制度安排将显著改变世界贸易格局[6]。我国已完成RCEP的核准[7]。RCEP于2022年1月1日起包括中国、日本、泰国、新加坡在内的10个国家正式生效。由此,对于跨境布局的企业,特别是以东南亚为主要布局区域的纺织企业[8]而言,如何在新的贸易规则安排下,实现对自身的跨境供应链网络规划,是相关企业“走出去”面临的紧迫问题,也是本文的研究重点。
国内外已有不少学者在全球供应链网络优化决策领域开展了相关研究。其中,早期研究起源于Hodder和Jucker[9]对全球工厂的选址问题研究。之后,Cohen和Lee[10]将其扩展为多阶段全球供应链布局模型。之后,引发了关于跨境选址-配送的大量研究,例如Christina等[11]研究了跨境的工厂以及配送中心的选址,及其之间的运输决策。Cohen和Lee[12]、Boujelben和Boulaksila[13]对相关研究进行了综述。在这些工作基础上,有学者从不同角度对经典选址-配送模型进行了扩展,其中,有相当多的研究考虑了跨境交易过程中的关税问题。如Wilhelm等[14]以北美自由贸易协定下美墨贸易展开研究,提出了一个混合整数规划模型解决关税影响下的供应链网络决策。汪传旭[15]考虑优化多阶段全球供应链网络,旨在实现基础设施成本、生产成本、关税成本等之和最小。Boujelben等[13]则综合考虑了关税、汇率、转移价格等因素。
但是,现有研究还存在一定的局限性。首先,考虑原产地规则的研究极少。文献[16]是为数不多的将原产地规则引入全球供应链网络优化的研究,但该研究只是考虑了原产地规则对原材料和产成品进出口配额的影响,并没有考虑相应的关税代价,以及企业如何通过供应链布局来规避对其不利的规则。更没有工作针对RCEP协定中区域累积规则带来的影响展开研究。其次,近年来,针对特定行业的研究引发了广泛的关注,如液氮[17]、有色金属[18]等,但针对纺织企业的全球供应链网络优化的研究还极为有限。
综上,本文针对纺织行业,研究跨境供应链网络优化决策。其中,在供应链网络优化方面,综合考虑多种纺织原料下的供应商选择、工厂选址、产能规划,以及采购、生产和运输决策;在跨境贸易因素上,重点关注原产地规则的影响,以及RCEP协定下的区域累积规则带来的影响。为此,提出了一个新的考虑原产地规则的混合整数规划模型。然而,由于原产地规则的考虑,使得构建模型为非线性。为最优求解,将其线性化为等价的线性模型,并设计了基于Benders分解的求解算法。最后,将模型应用于某纺织企业在东南亚建设面料生产线的决策上,通过对不考虑原产地规则、非区域累积的原产地规则和区域累积的原产地规则3种情况的对比,验证本文研究的有效性并得到相关管理结论。
1 跨境纺织供应链网络模型构建
1.1 问题描述
本文考虑由分布在不同国家的供应商、工厂和分销商组成的3级纺织供应链网络,如图1所示。其中,供应商提供生产所需的棉纱、涤纶、氨纶等纺织基础原料,工厂按给定的物料消耗表(bill of material, BOM)生产面料,并为全球的分销商提供产成品。为解决中国纺织企业“走出去”战略面临的相关决策问题,研究以工厂为主体,考虑其面临的工厂选址、产能规划、供应商选择、原料采购、产成品生产以及供应链网络各节点间的运输决策。
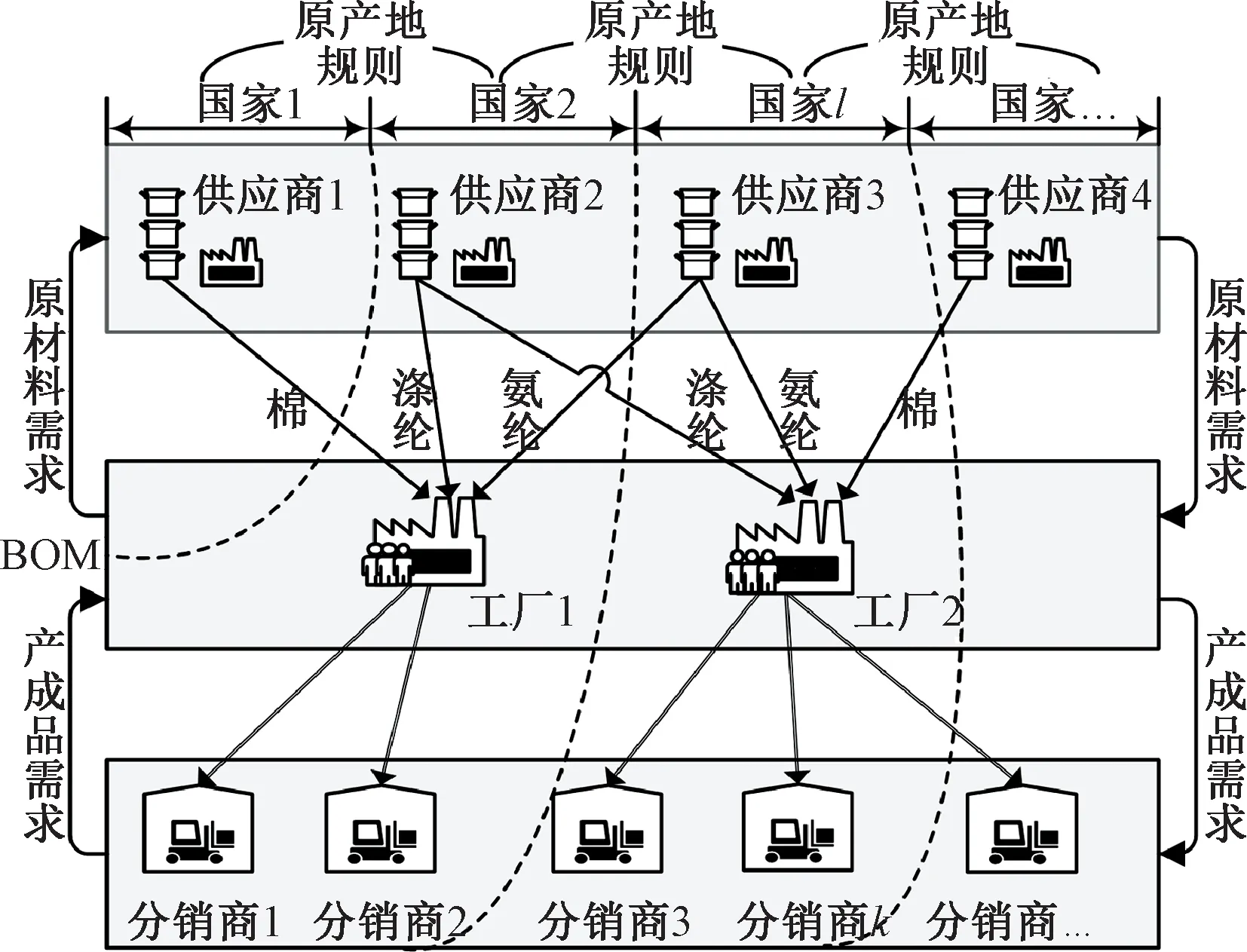
图1 跨境纺织供应链网络图
研究中特别考虑了原产地规则带来的影响。其中,采用基于增值百分比标准的原产地规则,即以某国家或地区对货物进行加工制造时,货物发生的价值增值(包括原材料、劳动力的价值以及其他资本价值的投入)不低于规定的比例α时,该货物的生产地才能被认定为该国家或者地区。令a为货物最终价值,b为非某国的材料价值,c为不明原产地的材料价值,原产地规则的概念公式可表达为
而RCEP采用的是更为友好的区域累积原产地规则,只要在15个成员国内的总价值增量不低于规定的比例40%时,便可认定为原产地货物,享有优惠关税。
综上,拟构建相应的优化模型解决上述相关决策,模型以利润最大化,即销售收入减去成本为目标。其中,成本包括工厂选址、产能建设、供应商选择、原料采购、生产、运输、缺货惩罚,以及受原产地规则支配的关税。
然而,由于原产地规则的考虑,导致所建模型为非线性。为实现对模型的最优求解,需对其进行线性化。为此,本文首先给出相关参数和变量说明;继而构建混合整数非线性规划模型,并将模型线性化;针对线性化后模型设计基于Benders分解的最优求解算法;最后将研究应用于实际问题的解决中,以展现其有效性。
1.2 变量说明
建模所需的集合、参数和决策变量如表1~3所示。

表1 集合说明

表2 参数说明

表3 决策变量说明
1.3 模型构建
构建考虑原产地规则的跨境纺织供应链网络模型,以企业利润最大化为目标。目标函数可大致分为销售收入、供应链布局成本、供应链运营成本以及关税成本4个部分。具体来说,销售收入为
P=∑j∑l∑k∑l′Vjlkl′·pjl
(1)
供应链布局成本包括了工厂选址与建设、供应商选择的代价:
(2)
供应链运营成本,包括了原料采购、生产、缺货、运输成本:
C2=∑m∑i∑lcmil·(∑j∑l′Qmiljl′)+
∑j∑lgjl·Gjl+∑k∑lskl·Skl+
∑i∑l∑j∑l′∑mqmiljl′·Qmiljl′+
∑j∑l∑k∑l′vjlkl′·Vjlkl′
(3)
关税的费用为
(4)
综上,供应链设计的优化目标可表示为
(5)
同时满足如下约束:
∑j∑l′Qmiljl′≤hmil·Xil∀i,∀m,∀l
(6)
∑m∑i∑lQmiljl′≤M·Yjl′∀j,∀l′
(7)
∑k∑l′Vjlkl′≤M·Yjl∀j,∀l
(8)
∑l″Amiljl′l″≤Qmiljl′∀m,∀i,∀l,∀j,∀l′
(9)
Gjl≤Ujl∀j,∀l
(10)
∑k∑l′Vjlkl′≤Gjl∀j,∀l
(11)
Skl′+∑j∑lVjlkl′=dkl′∀k,∀l′
(12)
(13)
rl″l′(∑m∑i∑lcmil·Amiljl′l″+gjl′·∑kVjl′kl″)≤
∑m∑i∑l=l′cmil·Amiljl′l″+gjl′·
∑kVjl′kl″+(1-Rjl′l″)·M∀j,∀l′,∀l″
(14)
∑m∑i∑l=l′cmil·Amiljl′l″+gjl′·∑kVjl′kl″≤
rl″l′(∑m∑i∑lcmil·Amiljl′l″+gjl′·∑kVjl′kl″)+
Rjl′l″·M∀j,∀l′,∀l″
(15)
Ujl,Gjl,Qmiljl′,Amiljl′l″,Vjlkl′,Skl≥0
∀m,∀i,∀l,∀j,∀l′,∀k,∀l″
(16)
Rjll′,Xil,Yjl∈{0,1} ∀i,∀l,∀j,∀l′
(17)
其中:式(6)为原材料供应与供应商选择的约束,即若供应商未被选中,则不能提供原材料;若选中,提供的原材料数量不能超过其产量约束;式(7)为原材料采购与工厂选址约束,其中M为一足够大正数,表示若l′国某工厂j不被选择则不进口原材料,被选择时则进口原材料;式(8)为产成品出口与工厂选址约束,若l′国某工厂j不被选中,则无法向分销商运输产品,若选中则可运输产品;式(9)为生产使用的原材料数量的约束,l′国某工厂j使用的来自l国某供应商i的某原材料m的数量不得超过该工厂从l国某供应商i进口的该原材料的数量;式(10)为工厂产能约束;式(11)表示运输量与产量约束;式(12)表示运量、需求和缺货数平衡约束;式(13)表示产成品和原料使用量约束;式(14)、(15)判断产成品是否满足原产地规则要求。当l′国某工厂生产的产成品满足l″国的原产比例要求时,Rjl′l″取值为1,否则,取值为0。式(16)和(17)是对决策变量取值的约束。
1.4 模型等价转化
在上述模型中,由于原产地规则的考虑,使得模型目标函数中的式(4)出现了非线性项,即决策变量Rjll′和Vjlkl′的乘积。为对其线性化,引入辅助变量,用于表示某工厂出口至l″国的产成品由于不满足原产地规则而需缴纳的关税额,即
此时,式(4)可表述为
(18)
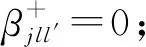
∀j,∀l,∀l′
(19)
(20)
1.5 基于Benders分解的算法设计
所建模型中包含了大量难求解的0~1变量,也存在如采购量、运输量、产量、缺货量等线性变量。为对其最优求解,考虑采用Benders分解[19]。该方法可用于解决大规模混合整数规划模型。其核心是根据变量类型的不同,将模型分解为只含有整数变量(也称复杂变量)的主问题和包含连续变量的子问题,以降低求解难度。并通过主子问题的迭代求解获得模型的最优结果。Benders分解自提出以来,就被广泛应用于各种场景的大规模问题求解中[20]。
为将Benders分解用于本文问题的求解中,将线性化后模型分解为主问题和子问题。首先,构建仅保留线性变量的子问题如下:
∑m∑i∑lcmil(∑j∑l′Qmiljl′)+
∑i∑lgjlGjl+∑m∑i∑l∑j∑l′qmiljl′Qmiljl′+
∑j∑l∑k∑l′vjlkl′Vjlkl′+∑k∑lsklSkl+
(21)
服从于式(6)~(15),(19),(20)。其中,整数变量可由主问题计算给出,是已知的,因此,子问题为标准线性规划。继而,由子问题,构造向主问题添加的最优Benders割,如式(22)所示:
(22)
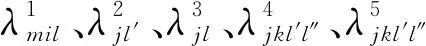
由此,可构造主问题模型为
服从于式(22)
Xil、Yjl、Rjll′∈{0,1} ∀i,∀l,∀j,∀l′
(23)
其中,式(22)为添加的最优割。由于本文允许缺货,即需求可不被满足,故而子问题总有可行解。所以无需向主问题添加可行割。

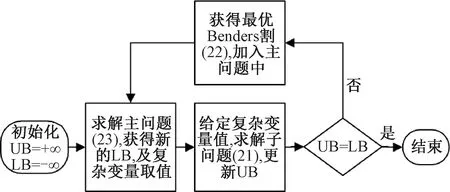
图2 Benders分解算法流程图
2 算例仿真与分析
2.1 仿真参数
本文考虑某纺织企业主要生产涤/棉/氨混纺面料。主打面料产品面密度为0.23 kg/m2,其中,涤纶(T)含量为62%,棉(C)为33%,氨纶(SP)为5%,具有良好的柔软性和透气性。由于东南亚地区与中国地理位置接近,且劳动力价格低、土地价格相对便宜,因而受到很多劳动密集型企业的青睐[8]。该企业为了能够享有东南亚地区的生产成本优势以及贸易协定优惠等,考虑将生产工厂布局至相关地区。
考虑10个工厂待选点,分别在越南(VIE)、缅甸(MYA)、印度尼西亚(INA)、泰国(THA)、柬埔寨(CAM)。该企业将在中国(CHN)、印度(IND)、澳大利亚(AUS)、越南和缅甸挑选棉纱供应商;在中国、印度、韩国(PRK)、日本(JPN)、印度尼西亚和泰国挑选涤纶和氨纶丝的供应商。生产的产成品将出口至中国、韩国、日本、印度尼西亚、泰国、越南、柬埔寨、缅甸和老挝(LAO),每个国家分别有2个分销商。产成品单位售价以美元计为9.6美元/kg。单位质量单位距离的运费为0.262美元/(1 kg·1 000 km)。假设运输成本与运输距离呈正比,供应链中各节点间的距离根据谷歌地图近似估算而得。其余相关数据如表4~6所示。表中缩写代表国家名,不同供应商用括号加数字区分,工厂用下划线加数字区分。

表4 供应商相关数据(选择成本、原材料价格、供货能力)
2.2 仿真结果
针对如下3种场景展开仿真:1)不存在关税减免,所有货物交易按照现行关税执行;2)采用非区域累积的原产地规则,实现的增值部分属于当地且超过40%,可视为原产地产品,享受关税免除;3)考虑RCEP协定中的区域累积原产地规则,即实现增值部分属于域内国家且累积超过40%,即可视为原产地产品,享受关税免除[21]。
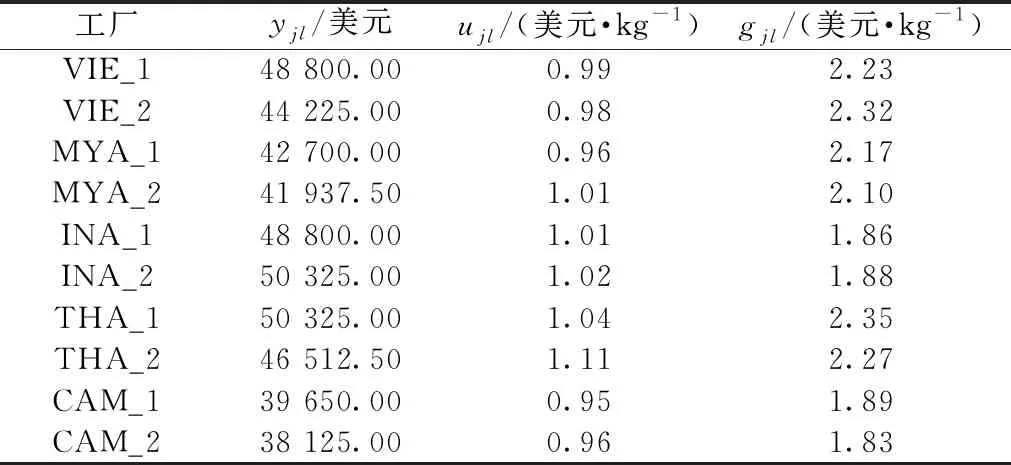
表5 工厂相关数据(选择成本、建设成本、生产成本)
在主频为2.6 GHz,内存为8 GB的笔记本电脑上,利用Visual Studio C++实现Benders分解算法。其中,算法迭代中的主子问题最优求解通过调用求解器ILOG CPLEX12.5实现。由此,得到3种场景的最优结果如表7所示。其中,工厂布局成本包括选择工厂的固定成本以及建设成本;采购成本包括原材料采购以及供应商选择成本;运输成本包括原材料以及产成品的运输成本。原材料采购量如表8所示,未被选中的供应商不在此表中显示。
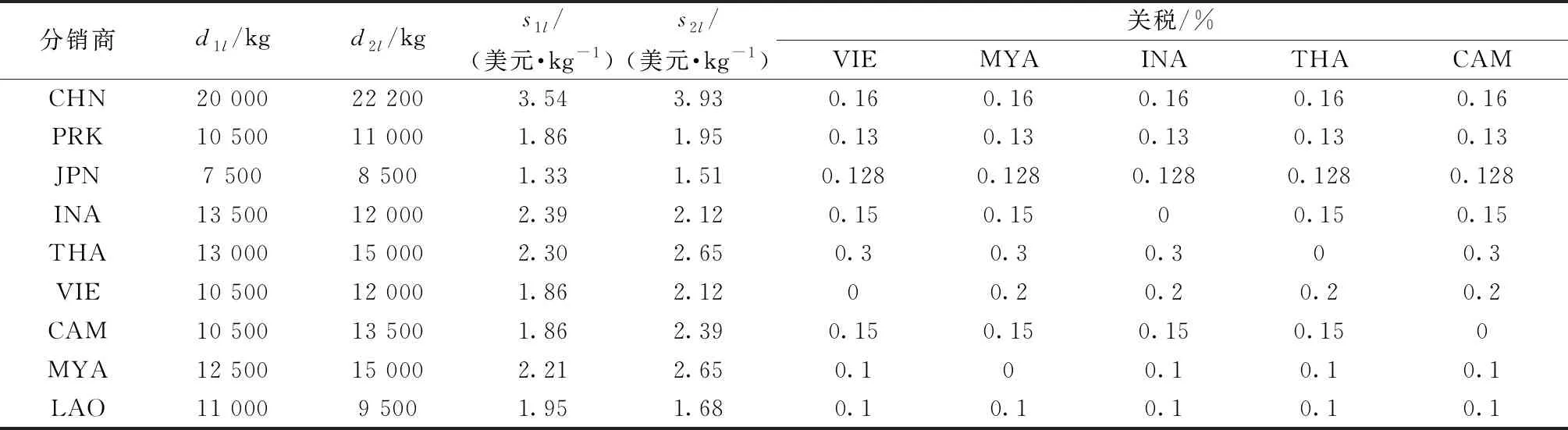
表6 分销商相关数据(需求、缺货成本、关税)
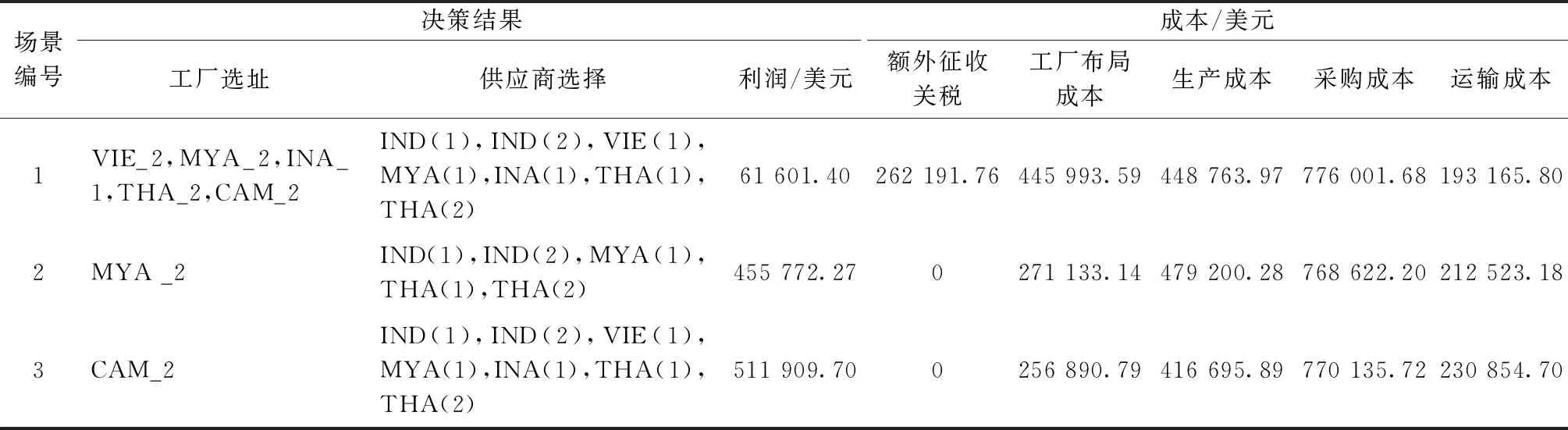
表7 不同场景下的最优解及最优决策
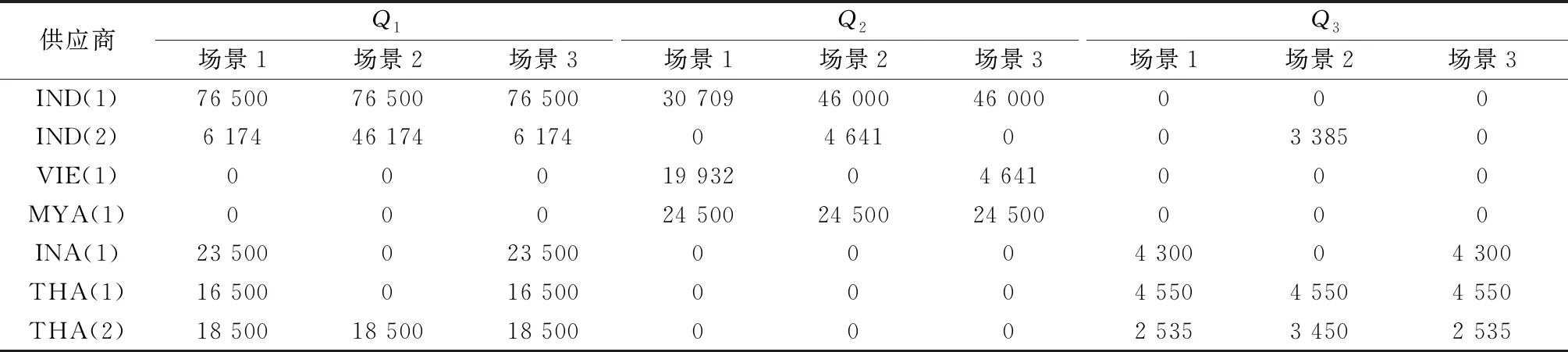
表8 不同场景下的原材料采购决策
通过上述的仿真结果发现,首先,在不考虑原产地规则的情况下,即场景1,不存在相应的关税减免。为尽可能降低关税带来的影响,在本文中,企业不得不在分销商,即主要市场所在的国家选建工厂(见表7)。显然,这会导致工厂布局成本增加,从而造成利润下降。
其次,在非区域累积的原产地规则下,优惠关税的存在会在一定程度上促进出口贸易,但原产地规则是基于特定国家的增值。显然,这会促使企业集中布局到具有产业集聚优势的国家,即该国同时具有较有竞争力的供应商和工厂待选点。由此,最终选择了工厂待选点MYA_2,同处一国的供应商MYA(1)也被选择,并产生了较大的采购量(见表7)。基于这些决策,实际生产的产成品实现了47%的原产比例,满足40%的政策要求。
第三,RCEP实施的是区域累积的原产地规则,即关注的增值是发生于RCEP成员国。显然,这一政策改变将赋予企业更为自由的选址及生产采购决策空间,更有利于实现全球供应链的最优配置。仿真结果也验证了这一点。具体来说,工厂选址于更具有成本优势的CAM_2。而该工厂所在地由于缺乏有竞争力的供应商,在场景2中是不会被选择的。此外,供应商选择则可综合其地理位置和供应商自身竞争力在域内国家自由布局,见表7。特别应当注意到,这一决策方案在场景2下,实际生产的产成品只能到达35%的原产比例,无法满足关税减免的条件。而在区域累积规则下,则可实现64%的原产比例。
此外,有必要说明,为与场景3中的基于区域累积的原产地规则作对比,场景2构造非区域累积的原产地规则,并假设所有国家均设定原产比例40%。这一假设与实际情况不完全一致。为此,下文对场景2的原产比例要求展开灵敏度分析。通过变化这一比例要求,得到企业利润与各工厂出口产成品达成的原产比例的平均值,如图3所示。
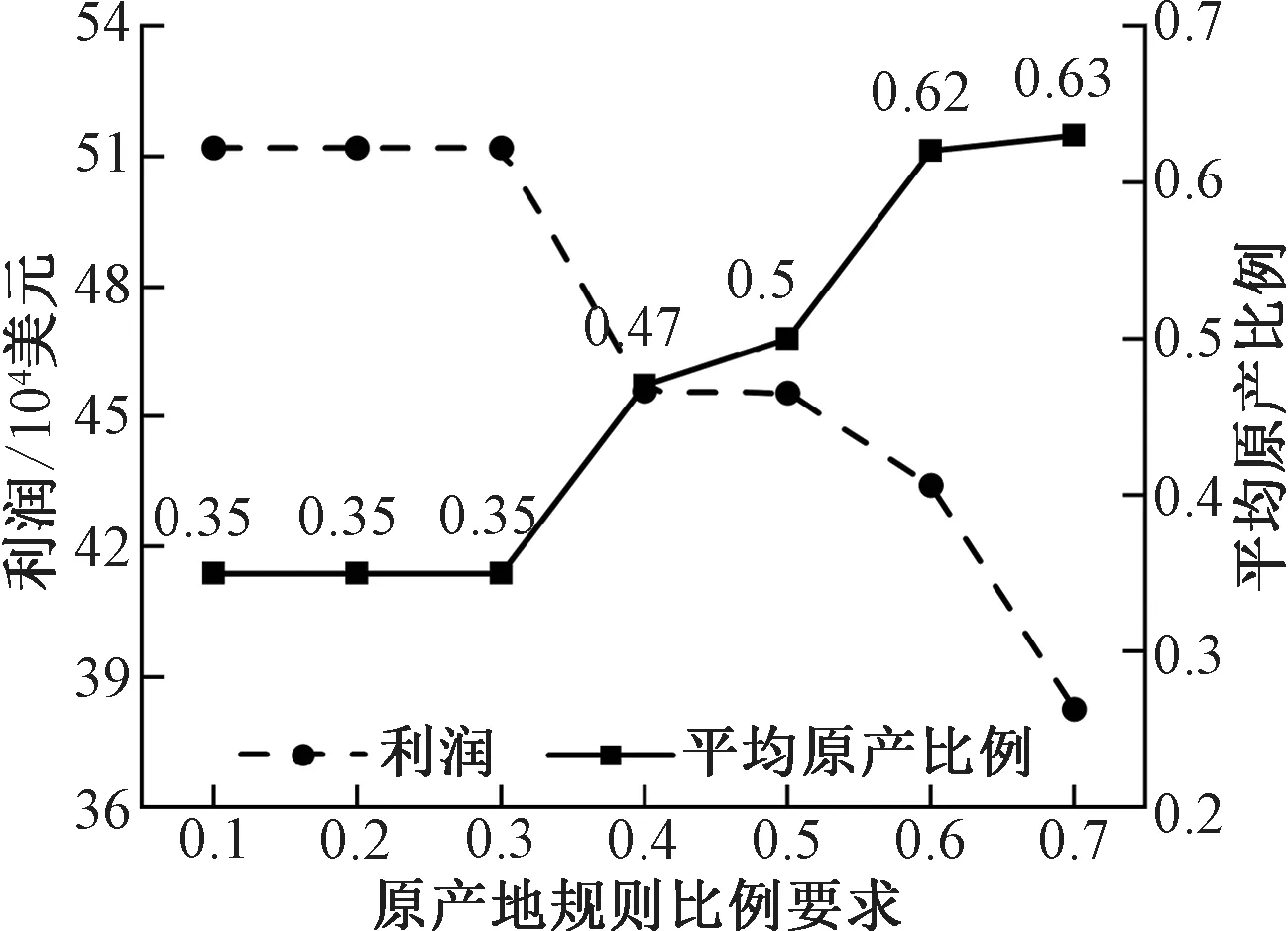
图3 基于原产地规则比例要求的灵敏度分析
由图3可知,随着原产地规则比例要求的变化,企业的利润和实际达成原产比例变换呈现相反的趋势。具体来说,当原产比例要求低于35%时,企业决策基本保持不变,此时产成品的实际原产比例可以达到35%。由于原产比例要求不高,企业可以相对自由配置供应链网络,因此利润也维持较高的水准。此时的利润基本与场景3中的结果一致,由此也体现了区域累积规则能够给相关企业创造的价值,但是,当原产比例要求高于35%之后,受限于这一要求,企业的供应链布局不断发生变化。由此,产成品的实际达成原产比例也相应提升,但利润在不断下降。
综合以上结果可知,原产地规则会显著影响决策者的供应链布局。在非区域累积规则下,具有产业集聚优势的国家会受到跨境布局企业的偏好。而RCEP的区域累积规则下企业可以在域内自由布局,减轻了关税壁垒对于跨境供应链利益实现的干扰,有望给企业带来更大的收益,但是,随着企业的跨境布局,在RCEP实施后,企业将面临着跨境运作和物流的挑战。
3 结束语
海外布局的制造企业面临原产地规则的制约和挑战。本文针对纺织企业,在考虑原产地规则以及RCEP协定的基础上,研究了包括工厂选址、产能规划、供应商选择、原料采购、成品生产,以及运输等在内的供应链网络设计决策。为此,构建了相应的混合整数非线性规划模型。为实现对模型的最优求解,先将其线性化,然后设计了基于Benders分解的最优求解算法。最后,通过将其应用于某企业的海外布局决策中,对于包含RCEP协定的3种情况进行了仿真对比,验证了本文工作的有效性,也分析了原产地规则,特别是RCEP协定中区域累积规则所带来的影响。
由于跨境贸易影响因素众多,在后续的研究中,结合重要而紧迫的因素,如人民币国际化、贸易摩擦等展开研究,是未来的一个可能的方向。在这些因素中,有相当一部分存在不确定性,由此,根据随机因素特征的不同,选取合适的不确定优化方法展开供应链网络的优化设计,这也是未来的主要研究内容。

