基于岭回归方法的羊毛衫洗后特征感性评价

赵 馨， 王彩霞， 周小皮， 丁雪梅

(1. 东华大学 服装与艺术设计学院， 上海 200051； 2. 东华大学 现代服装设计与技术教育部重点实验室， 上海 200051; 3. 松下家电(中国)有限公司， 浙江 杭州 310018)

感性是基于人体五官感觉和大脑认知的综合心理学概念[1]。消费者的感性评价是一个复杂的综合判断过程[2-3]，常被认为只能定性、难以量化、非理性且无逻辑。感性工学研究是运用现代计算机辅助、数理统计等方法，将消费者对产品的感性认知转化成具体量化的产品设计要素的过程[4]。其研究结果不仅可帮助研发企业精准定位消费者的关注重点，而且可以及时了解产品功效是否与消费者需求相匹配，能够极大地降低新产品开发的风险。

目前，感性工学被普遍应用于服装[5]、家具[6]、生产装备[7]等各类产品[8]研发中，尤其是服装设计中，例如采用感性工学方法进行旗袍图案设计[9]、针织服装领型的设计[10]、女装色彩搭配[11]、运动内衣款式设计[12]、袜子图案设计[13]、生理内裤设计[14]等研究。通常，感性工学的研究过程可概述为以下4个步骤：1)调查、实验等方法确定产品的设计要素；2)通过调研、访谈等方法获得消费者对产品的感性诉求；3)感性评价数据分析，构建感性工学系统；4)使用感性工学系统进行产品开发。其中，通过数据分析，建立消费者对产品某一种或多种特征与整体印象感性评价之间的量化关系，是一个非常重要的成果输出，不仅可帮助产品研发企业精准定位消费者的关注重点，而且可预测消费者对产品功效的感性评价，对研发企业具有重要意义。

通常情况下，多种变量间相互依赖的定量关系采用最小二乘线性回归法求解，普遍应用于生物科技[15]、环境[16]、水文预测[17]等众多领域，但当变量之间存在显著共线性关系时，需要使用最小二乘线性回归法的改良方法，即岭回归方法。例如，人口规模、经济增长以及技术进步之间相互制约与影响，3组数据之间存在多重共线性关系，张国兴等[18]使用岭回归方法得出三者之间的量化关系；同样，岭回归方法也曾被用于探究东北三省大豆与玉米生产替代关系[19]、估测肉牛体重[20]，以及预测短时交通流[21]等问题。

在纺织服装的感性评价研究中，服装不同特征的感性评价之间也存在相互制约的共线性关系，如当平整度感性评分较低时，服装的尺寸比例感性评分也会较低，导致整体印象感性评分也会越低，然而，消费者对服装多种特征与其整体印象感性评价之间量化关系的研究方法尚未见报道。本文基于松下家电(中国)有限公司对新型洗涤设备的研发背景，以多种洗涤方式处理的羊毛衫为对象进行感性评价，并采用岭回归数据分析方法，建立羊毛衫洗后多种特征与整体印象感性评价之间的量化关系，研究结果对新型洗涤设备的优化研发具有重要的指导作用。

1 实验过程

1.1 实验材料

选用浙江康赛妮集团有限公司生产的未经防缩处理的粗纺羊仔毛纱线，由新奥毛衫厂(浙江嘉兴)使用针号为12的针织横机织造，共计17件同款同色的经典套头款羊毛衫，号型均为160/84A，颜色为米白色，羊毛衫大身为纬平针组织，领口、袖口、下摆为螺纹组织，具体参数见表1。

表1 羊毛衫参数

根据Woolmark TWC-TM309《“手洗”羊毛产品在滚筒式干衣机中的性能测试方法》与GB/T 4288—2018《家用和类似用途电动洗衣机》，首先将所有羊毛衫在水温40 ℃、液体洗涤剂质量浓度为1 g/L的水中浸泡30 min，然后冲洗2次并平铺晾干，以消除羊毛衫织造中产生的应力。保留1件预处理后的羊毛衫作为洗前的标样，即评分为5分的标准样品，如图1所示。剩余的16件羊毛衫分别经过新型洗涤A、轻柔机洗B、手洗C、常规机洗D 4种洗涤方式各完成1、3、5、10次的洗涤。新型洗涤是一种通过气囊产生轻柔打击动作的洗涤形式[22]，具体可参考文献[22]。常规机洗与轻柔机洗分别指的是使用松下洗衣机(XQG100-EG128)进行棉程序与羊毛程序的洗涤。手洗程序由松下公司根据中国消费者的手洗调研数据设计制定，具体为经过训练的实验者以2 s/次的频率抓、放浸泡的羊毛衫1.5 min。然后，用手将样品从洗涤剂溶液中拎起、再放回到溶液中，如此漂洗8个循环，重复以上漂洗动作2次。最后，使用滚筒洗衣机以500 r/min的转速脱水。

图1 评分为5分的羊毛衫

羊毛衫平铺晾干后，陈列在号型为160/84A的人台上，如图2所示。依据洗涤方式与洗涤次数样品命名，方法：字母A、B、C、D分别表示洗涤方式，数字表示洗涤次数，如A-1代表经过A洗涤方式洗涤1次的羊毛衫。可观察到，经过洗涤处理后的16件羊毛衫在尺寸比例、领口形态、下摆形态、大身平整度、弹性等特征均出现了不同程度差异，其中，D-3、D-5、D-10这3件样品尺寸显著收缩，不具有服用性，因此不用于感性评价，剩余13件洗后羊毛衫及原样共计14件羊毛衫作为感性评价样品。

图2 洗涤处理后的羊毛衫人台陈列图

1.2 羊毛衫感性评价

3位服装专业测评人员通过观察、轻轻触摸等方式提炼出14件羊毛衫的9种显著特征，具体为尺寸比例、领口形态、下摆形态、袖窿接缝(服装大身与袖片的接缝)平整度、大身平整度、起毛起球、磨损程度、弹性、蓬松度。测评人员根据羊毛衫整体的优劣感受，综合给出整体的感性评价，即为整体印象。综上，羊毛衫感性评价的调查问卷为以上样品的9种特征和整体印象，共计10项评价内容。

采用李克特量表对每道评价内容进行5分评分设置，从1～5分，消费者对羊毛衫特征或整体印象的心理接受度逐渐增加，分别为效果非常差、效果较差、效果一般、效果较好、效果非常好，评分精确至小数点后一位。当评分为4分以上时，测评者认为是可直接穿着外出，不需要熨烫等整理。

生活中购买洗护用品与服装的用户多为女性，因此本文通过调研公司招募了上海地区30名25～55岁，有穿着与洗涤护理羊毛衫习惯的女性作为羊毛衫感性评价的测评人员。

参照GB/T 10220—2012《感官分析 方法学 总论》, 感性评价实验前，向测评人员解读问卷内容和评价语义标尺，防止歧义混淆。实验室环境光线稳定均匀、温湿度适宜，且避免评价人员看见样品陈列等准备过程。然后，测试人员依次进入感性评价实验室，首先展示5分标准样品(见图1)。然后，测评人员依次观察陈列的13件羊毛衫(见图2)，并完成每件羊毛衫所有评价内容的评分。在评价期间，测评人员可以来回自由观察、用手轻轻触碰面料，但不可交流。实验室内安排有3～5名工作人员，进行现场答疑与管理。实验结束后，回收所有问卷。

2 洗后羊毛衫感性评价数据分析

2.1 感性评价结果

为检验调研数据的有效性，即检验30名测评人员之间的评价标准是否一致，将数据使用多配对样本的Kendall协同系数检验，结果见表2。

表2 Kendall′s W检验统计量

表2显示，Kendall′s W协同系数为0.6，大于0.5，接近1，检验概率P值小于显著性水平0.05，意味着30名测评人员对14件羊毛衫的感性评价一致性较显著，调研数据均为有效数据。

表3为羊毛衫感性评价结果统计表。其中，X1、X2、X3、X4、X5、X6、X7、X8、X9、Y分别为尺寸比例、领口形态、下摆形态、袖窿接缝平整度、大身平整度、起毛起球、磨损程度、弹性、蓬松度、整体印象的评价值。可看出羊毛衫的尺寸比例、领口形态、下摆形态、大身平整度、弹性等特征的感性评分均呈现出不同程度的差异，与羊毛衫人台陈列图的效果一致。羊毛衫的9种特征与整体印象评价值的变化趋势基本一致。对比表3中X1、X2、X3、X4、X5、X6、X7、X8、X9、Y的数据变化趋势，发现整体印象数据趋势与大身平整度、弹性的数据趋势一致性较好，可初步判断羊毛衫的大身平整度、弹性对整体印象的感性评价有较强相关性，即较强影响作用。同时，10组感性评价数据的两两相关性系数均在0.8以上，且相关系数检验概率P值(显著性双侧)都近似为0，也反映了羊毛衫多种特征感性评价数据之间可能存在共线性问题。

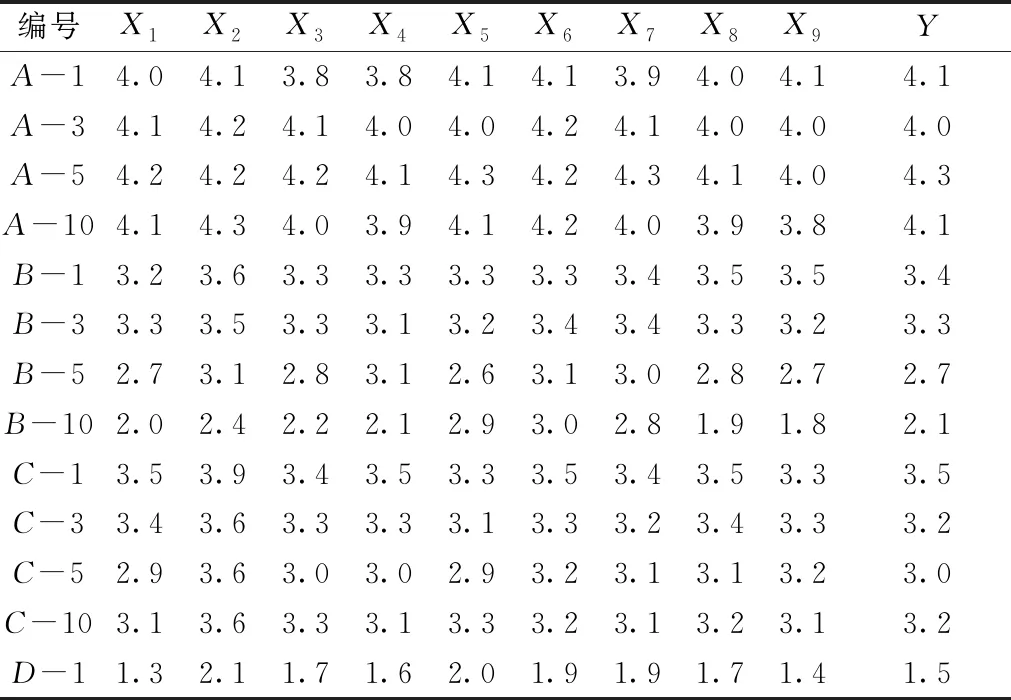
表3 羊毛衫感性评价结果统计表

2.2 感性评价之间量化关系

为了建立羊毛衫多种特征与整体印象感性评价的量化影响关系，首先采用最小二乘法线性回归分析，回归模型表示为

Y=Xβ+ε

(1)

式中：Y为因变量;X为自变量;β为回归系数;ε为误差。

如果回归系数β按照最小二乘法的估计，则:

β= (XTX)-1XTY

(2)

式中：基于式(1)假设，X不一定是方阵，因此两边乘以X的转置矩阵XT，再取其逆矩阵。当矩阵XTX非奇异，则β有唯一解。得到最小二乘法线性回归拟合精度与模型，具体见表4与表5。

表4 最小二乘法线性回归拟合精度

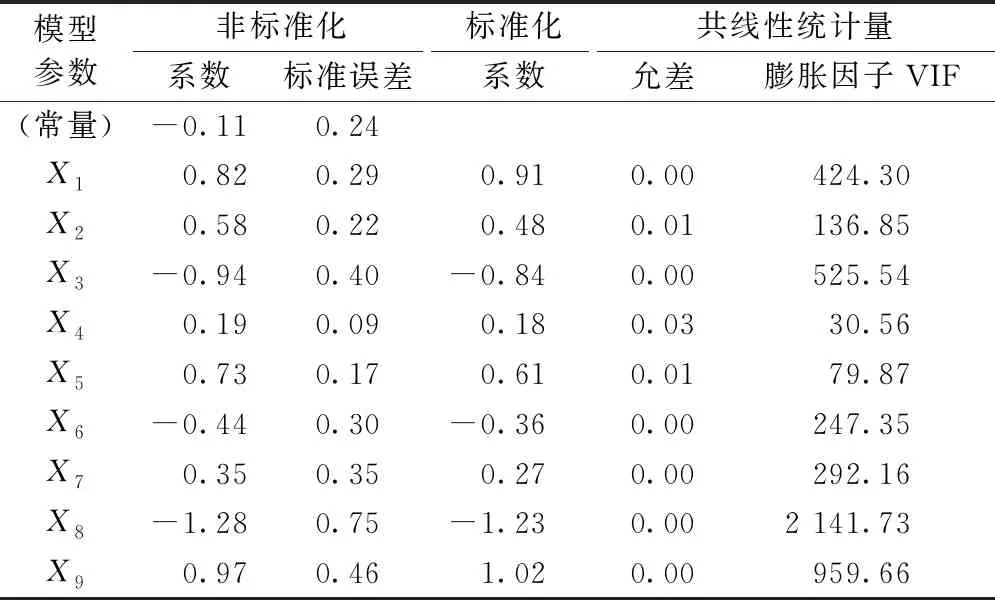
表5 最小二乘法线性回归模型

表4中，R2为决定系数，描述回归曲线对真实数据点拟合程度的统计量，调整后R2是R2决定系数加上残差自由度后的重新计算结果，表示模型的拟合精度。调整后R2为0.997比较接近1，拟合度较高。

非标准化系数与标准化系数均为回归系数，标准化是去除量纲的，体现了变量间的相对重要性，只用于自变量进行比较。解释自变量对因变量的作用时，使用非标准化的回归系数β。标准估计误差是指因变量各实际值与其估计值之间的平均差异程度，其值越小，回归方程的代表性越强。在非标准化系数列中，X3、X6、X8的系数为负数，即下摆形态、起毛起球、弹性效果评分越高时，整体印象评分越差，这与实际逻辑不符，无法用专业知识来解释。此外，共线性统计是衡量变量之间存在相关性的严重程度，当允差与膨胀因子VIF的值接近0和大于10时，说明整体印象Y与其他解释变量的多重共线性很严重[23-24],因此该模型不可用。

改用岭回归方法求解，回归系数β为

β= (XTX+kI)-1XTY

(3)

式中：k为岭回归参数，k∈[0，1]，k=0，即为最小二乘法估计；I为单位矩阵。

其原理是给矩阵XTX加上一个对角阵，尽量将奇异矩阵(XTX)转化为非奇异矩阵(XTX+kI)，以使矩阵XTX尽可能可逆，以便能够求出回归系数，提高参数估计的稳定性和可靠性[25]，得到更真实的、反映客观实际的参数。k越大，消除共线性影响效果越好，但拟合方差越大，拟合精度越低,因此，必须在消除共线性与提高拟合精度二者之间找到最佳平衡点，使k既能足够消除共线性对参数估计的影响，又尽可能提高拟合精度。

运用数据处理软件工具，设定迭代步长为0.01，运行得到岭迹图，如图3所示。其中横坐标为岭回归参数k，纵坐标为岭回归系数估计值。

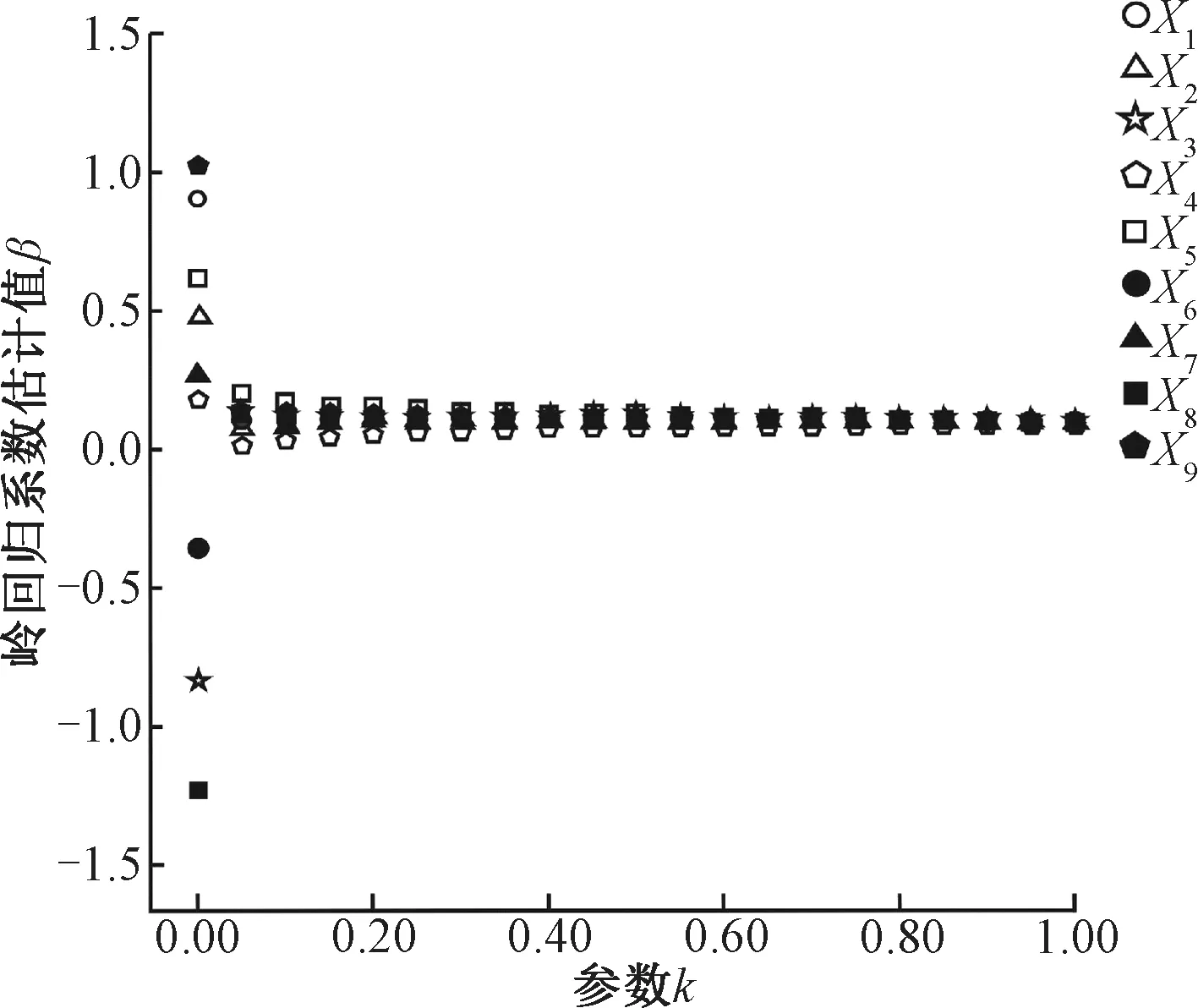
图3 岭迹图

k选取的原则是: 在岭轨迹变化趋于稳定时选取其最小值。从图3可见，当k=0.20 以后，自变量系数基本不变。故设置k=0.20，得到岭回归结果，具体见表6、7。

表6 岭回归拟合精度

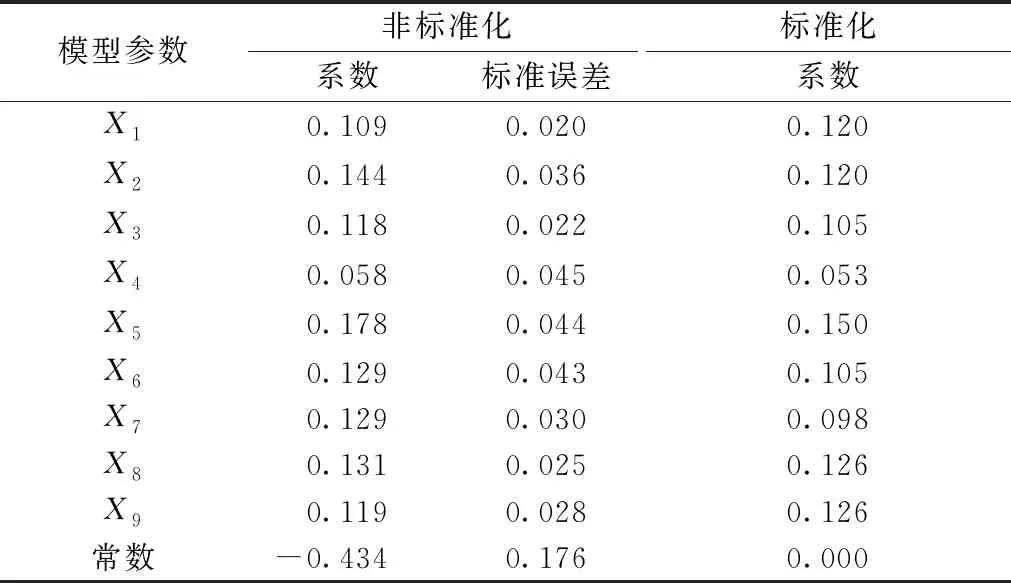
表7 岭回归模型

Y=0.109X1+0.144X2+0.118X3+0.058X4+

0.178X5+0.129X6+0.129X7+

0.130X8+0.119X9-0.434

(4)

岭回归方程中，自变量的标准化系数皆为正数，符合逻辑，反映了它们对因变量的影响。将样品的多个特征感性评价数据代入岭回归方程式(4)得到羊毛衫整体印象的岭回归预测值，图4为羊毛衫整体印象的调研值与岭回归预测值的对比图。显示2组数据值十分接近，回归模型拟合度非常好，拟合度为0.977，能够准确预测消费者对羊毛衫整体印象的感性评价。

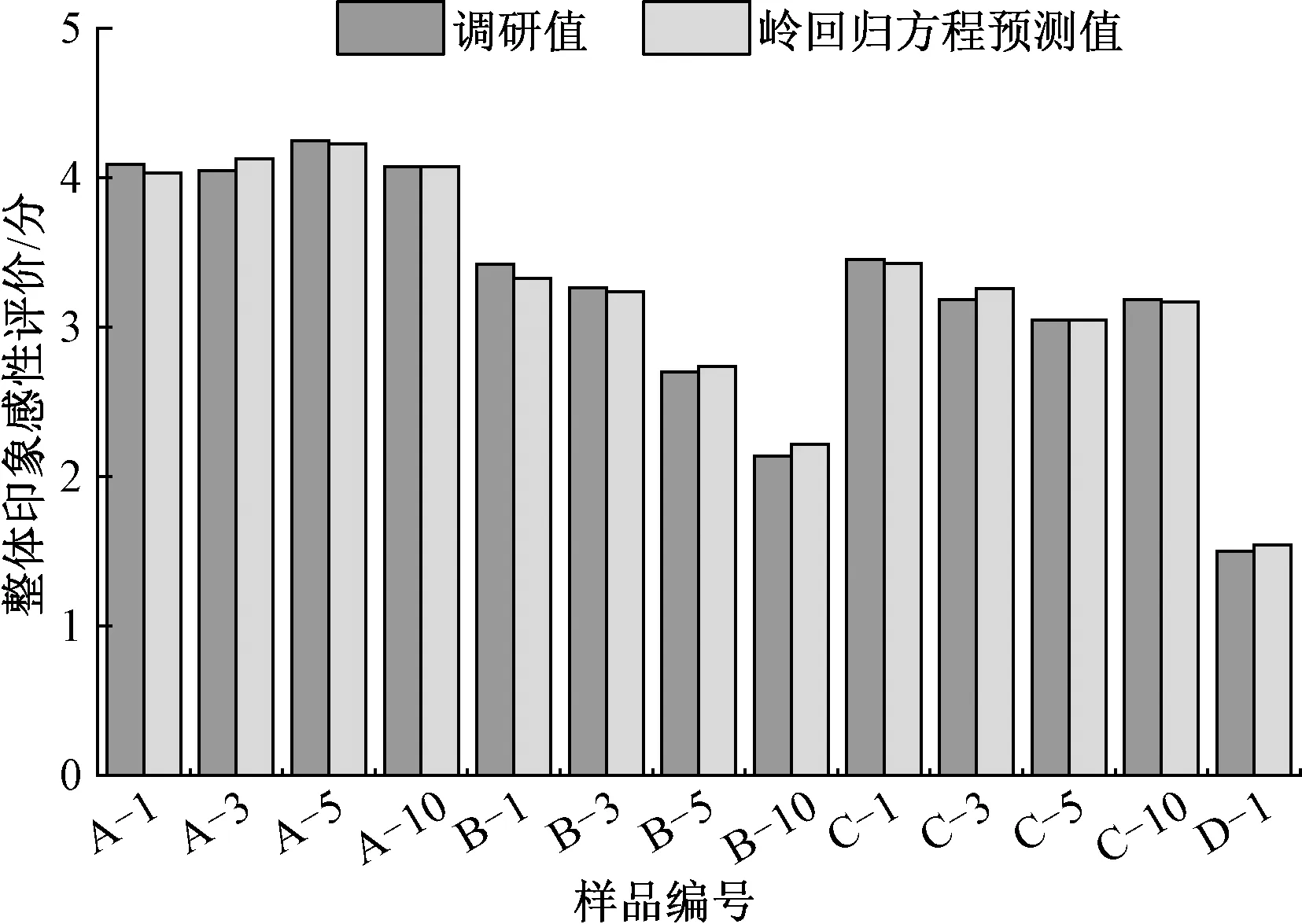
图4 羊毛衫整体印象调研值与岭回归预测值的对比图

以上岭回归结果显示，大身平整度和袖窿接缝平整度是消费者对套头款羊毛衫整体印象感性评价最重要和最不重要的影响因子。大身平整度及服装前后片部位，视觉面积较大，因此导致大身平整度是羊毛衫整体印象感性评价的最重要影响因素，同时，由于消费者观察习惯，较少关注服装肩部袖窿接缝位置[26]，因此，羊毛衫袖窿接缝平整度对服装整体印象效果的影响较小。此外，尺寸收缩十分显著的3件羊毛衫未参与感性评价实验，而参与感性评价的14件羊毛衫在尺寸比例方面差异不显著，故尺寸比例对整体印象的影响权重位于第4位。

基于岭回归方法的羊毛衫感性评价研究结果，既能表明服装不同特征对整体印象感性评价的影响权重，也能表明它们之间的岭回归方程式。根据影响权重大小，研发企业可识别出消费者对该类型服装的关注重点，如上文研究显示，平整度对羊毛衫整体印象评价具有较高的影响权重，即为消费者对羊毛衫护理重点是平整度，企业可以有针对性地进行平整度相关的优化设计；此外，岭回归方程可定量地预测消费者对产品功效的感性评价，及时帮助企业了解产品功能是否始与消费者需求相匹配，极大地降低新产品开发的风险，提高产品的研发效率。通常越大的样本量更能准确地反映事物之间的逻辑关系，本文问卷设计和问卷收集的样本量均为最低，在后续的研究中这方面有待改进。

综上，岭回归方法能够将消费者对产品的感性评价规律转化成具体的量化关系，是一种良好的感性工学研究方法，可广泛用于不同类型产品的感性工学研究中。

3 结 论

通过现场问卷调查，得到30名消费者对羊毛衫整体印象及9种特征的感性评价，研究结果如下。

1)羊毛衫不同特征及整体印象的感性评价数据的两两相关性系数均在0.8以上，且最小二乘线性回归分析也显示，服装感性评价数据存在显著共线性问题，因此，最小二乘线性回归法不适用于建立感性评价数据间的量化关系。

2)改用岭回归方法分析，得到羊毛衫9种特征对整体印象感性评价的影响权重排序为：大身平整度、弹性、蓬松度、尺寸比例、领口形态、下摆形态、起毛起球、磨损程度、袖窿接缝平整度，影响权重分别为0.15、0.126、0.126、0.120、0.120、0.105、0.105、0.098、0.053。

3)羊毛衫9种感官特征的感性评价与整体印象感性评价的量化关系为Y=0.109X1+0.144X2+0.118X3+0.058X4+0.178X5+0.129X6+0.129X7+0.130X8+0.119X9-0.434，岭回归方程拟合度为0.977，岭回归模型拟合度非常好。

4) 研究证明了岭回归方法适用于建立具有共线性关系的服装感性评价的量化关系，可广泛应用于不同产品的感性工学研究。