一种孤岛直流微网等微增率下垂控制方法*
孙峰洲
(国网福建省电力有限公司经济技术研究院,福建 福州 350012)
0 引言
随着直流负载利用率的不断提高及光伏发电系统和燃料电池等直流分布式电源(distributed generations,DGs)的普及,能高效集成直流源荷,实现功率集中调控的直流微网受到广泛关注[1]。在孤岛直流微网中,各台分布式电源需要在没有主网提供功率支撑的条件下,保持直流母线电压稳定,并按比例实现负荷功率的自适应分担[2]。P-V下垂控制是直流微网分布式电源的一种常用控制方式,但在传统下垂控制方式下,直流母线电压在负荷波动时会产生稳态电压偏差,导致供电质量下降[3]。同时,由于不同分布式电源的发电特性差异,无法保证发电成本实现最优化[4]。
为了减小传统下垂控制引起的电压偏差,相关文献提出电压二次控制方法来改善电压质量[5]。Mazumder等[6]通过调整传统下垂控制的电压设定值,实现集中二次控制。然而,该控制方式需要依赖中央控制器的实时通信,降低了系统的可靠性。Anand[7]提出了分布式二次控制,可在本地控制器中实现电压设定值调整,有效避免集中控制下中央控制器故障带来的影响,Nasirian等[8]在此基础上提出了一种改进电压二次控制方法,以进一步改善负荷频繁波动条件下直流母线电压的稳定性。上述研究工作主要集中于改善直流母线电压质量,而没有充分考虑系统的经济运行。Nutkani[9]提出了一种并网型直流微网分布式电源功率自适应分配方法,考虑了各分布式电源不同额定容量与发电成本曲线的影响,但该方法需要大电网提供直流母线电压支撑,不适用于孤岛直流微网。Nutkani[10]提出了分布式电源非线性下垂控制方法,并采用集中式智能优化算法最小化孤岛交流微网的运行成本,但微网中任意源荷接入与退出都需要重新求解整个优化问题,系统可拓展性较差。Xin等[11]进一步引入了电压三级控制,在补偿母线电压偏差的同时保障系统经济运行。然而,为实现多个控制器的动态解耦,该方法的暂态响应较为缓慢,且无法完全消除稳态电压偏差。
针对上述问题,为兼顾微网经济运行和直流电压恢复,本文提出了一种孤岛直流微网等微增率下垂控制方法,在下垂控制策略中增加了发电成本微增率(cost incremental value,CIV)的时滞前馈路径。在第一阶段,各分布式电源基于等微增率原则响应负荷波动;在第二阶段,由时滞环节实现直流母线电压自适应恢复。此外,为进一步提高系统的可靠性,提出了基于该下垂控制方法的即插即用策略。
1 等微增率下垂控制方法
典型孤岛直流微网拓扑示意图如图1所示,多种不同类型的分布式电源通过DC/DC变流器连接到直流母线,分布式电源在分担负荷功率的同时需要维持直流母线电压稳定。P-V下垂控制是直流微网中最为常用的分布式电源控制方法,其下垂方程如下:
(1)
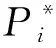
然而,传统下垂控制在负荷波动时会不可避免的产生直流母线电压偏差,且由于不同分布式电源的发电成本曲线差异,按额定容量比例分担负荷功率无法保证微网运行经济性最优。为了使总发电成本最小化,需要在下垂控制环节中考虑不同分布式电源的发电成本函数。一般而言,分布式电源的发电成本包括维护成本、燃料成本、排放罚款和空载成本等,其函数可表示为:
(2)
式(2)中,ai,di,ci,bi,yi表示成本系数。
成本微增率函数是发电成本函数的导数,表示为:
λi(Pi)=aiPi+bi·eyiPi+di
(3)
在孤岛微网中,系统各分布式电源可基于等微增率原则运行实现总发电成本最优[10]。为了克服传统下垂控制的缺点,并实现控制环的简化,本文提出了一种基于时滞前馈环节的等微增率下垂控制方法,各台分布式电源的下垂控制框图如图2所示。
如图2所示,对第i台分布式电源,其具体下垂控制方程表示为:
(4)
(5)
式(5)中,T表示延迟时间常数;w表示低通滤波常数。
与传统下垂控制相比,本文提出的λ-V下垂控制以发电成本微增率作为下垂控制变量,以微增率的时滞前馈项作为下垂参考值,间接调整发电功率以实现系统经济运行。值得说明的是,为保证等微增率原则成立,各台分布式电源的下垂控制参数均设为统一变量,即具有相同的直流母线电压参考值udcref和下垂系数k。此外,假设变流器出口线路阻抗R2,i已知[9]。
图3展示了当负荷在t=0出现阶跃增长时的下垂控制时序。本文提出的下垂控制暂态响应过程可以分为两个阶段,阶段I从0到T时刻,为等微增率控制阶段;阶段II从T到T2时刻,为电压恢复控制阶段。T2定义为电压恢复时间。A表示初始运行点,B表示电压恢复启动点,B表示电压恢复完成点,此时系统重新达到稳态。
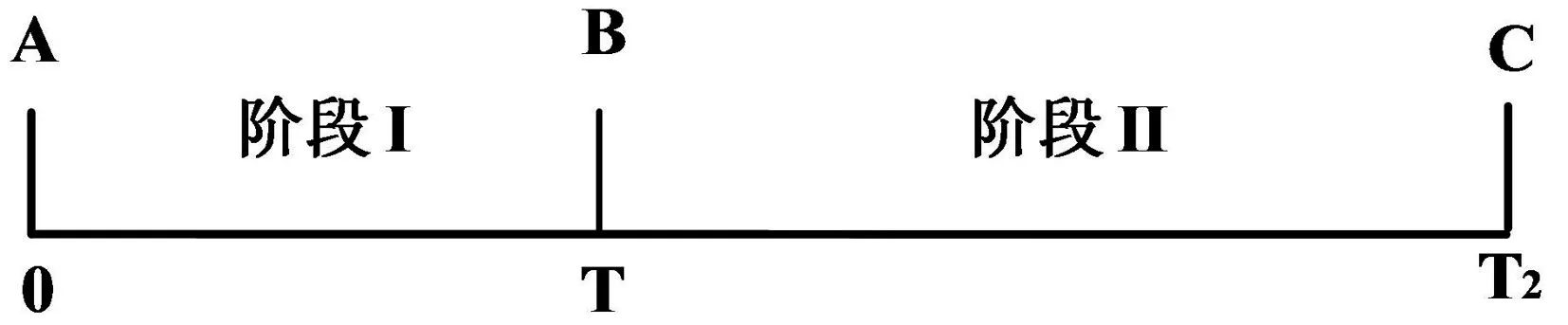
图3 下垂控制时序
(1)等微增率控制阶段
假设变流器实际出口电压能始终跟随电压指令值,则根据式(4),直流母线电压可以表示为:
(6)
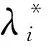
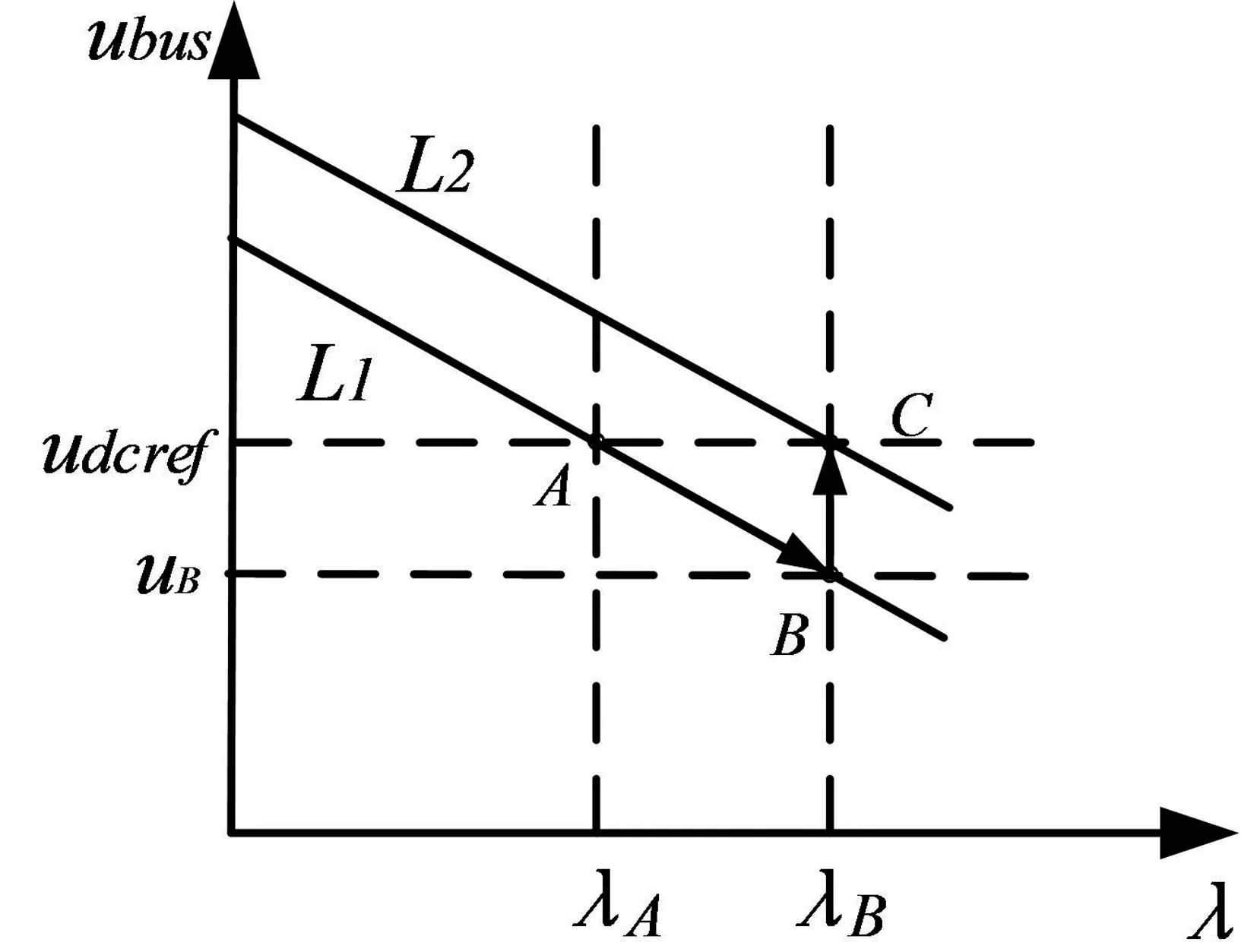
图4 λ-V下垂控制曲线
(2)电压恢复控制阶段
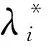
x(t)=1-e(-t/w)
(7)
当追踪误差小于0.5%时,响应时间约等于6w,所以总电压恢复时间为:
T2=T+6w
(8)
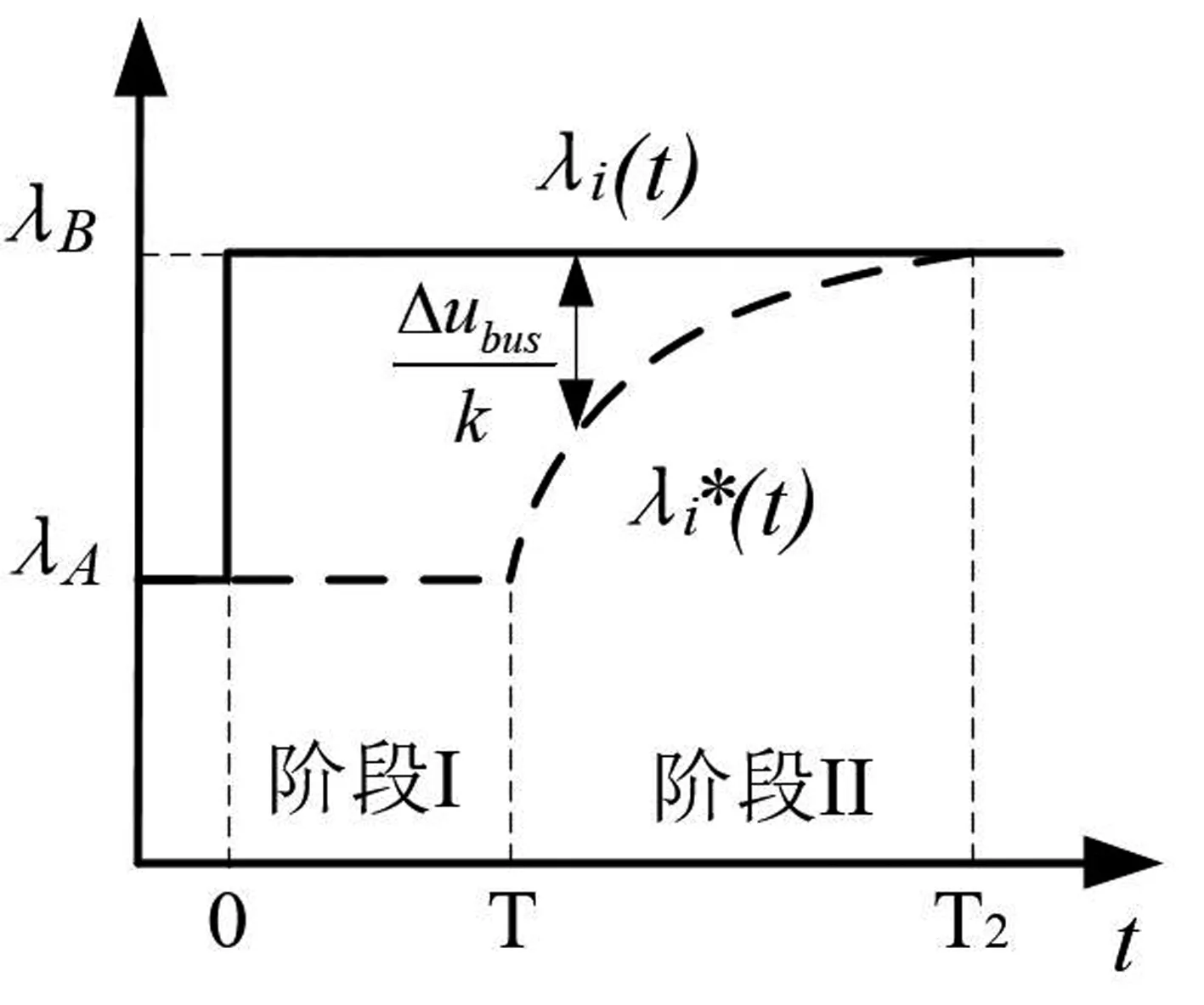
图5 电压恢复过程
2 即插即用控制策略
为进一步提高系统的可靠性与拓展性,基于上述等微增率下垂控制方法,本文提出了两种即插即用控制策略,分别为无需通信的分散式即插即用策略和基于通信的分布式即插即用策略。
2.1 分散式即插即用策略
当一台新的分布式电源接入直流微网分担负荷功率时,已经并网的分布式电源发电功率会下降,由式(6)可知,直流母线电压会上升。因此,各台分布式电源可通过检测直流母线电压的幅值和变化率,实现控制模式的切换,控制切换标准为
(9)
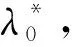
基于上述控制,各分布式电源仅依靠本地信息,无需通信即可实现即插即用功能。但是,该策略无法分辨直流母线电压的变化是因分布式电源接入还是由于负荷变化所致,因此当负荷产生较大突变时该控制策略同样会被触发,从而加剧直流母线电压的波动。
2.2 分布式即插即用策略
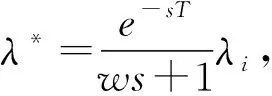
值得说明的是,延迟时间T2的设置是为了保证控制的无缝切换,在控制切换时不产生大的功率扰动。与分散式即插即用策略相比,基于分布式通信时系统直流母线的电压稳定性和暂态响应性能均可得到改善,且不会受到负荷波动的影响。
3 小干扰稳定分析
本节通过建立等微增率下垂控制的小信号模型,对孤岛直流微网的稳定性进行分析。本文中,采用一阶Padé近似对时延环节进行近似,如式(10)所示:
(10)
由图2可列出基于等微增率下垂控制的分布式电源小信号模型,表示为:
(11)
设3台分布式电源接入直流母线,孤岛直流微网示意图如图6所示,各分布式电源对应发电成本微增率曲线如图7所示。
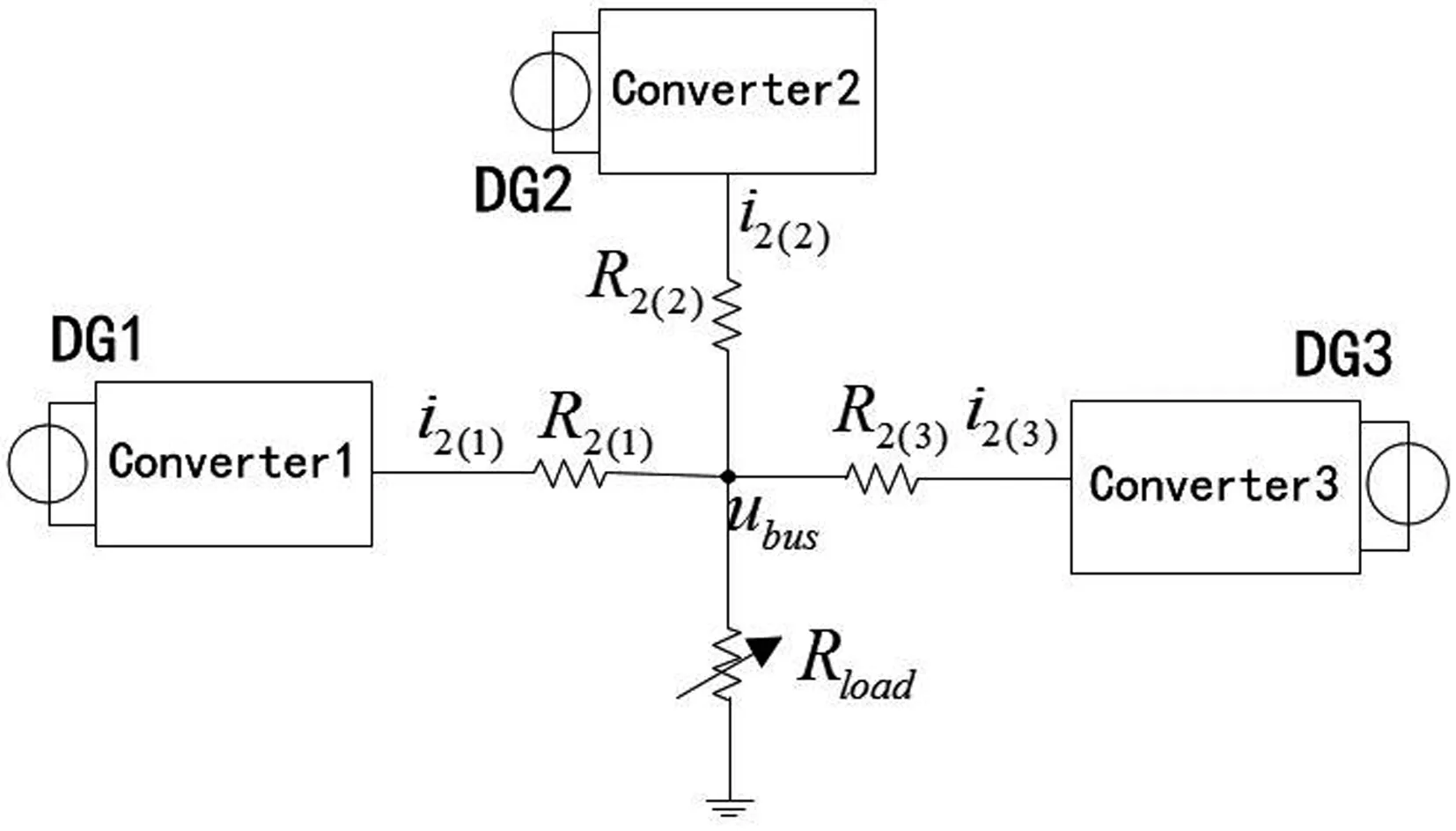
图6 直流微网结构图
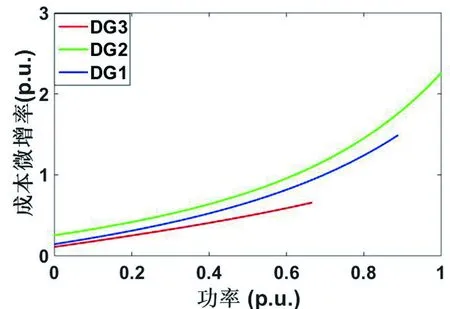
图7 分布式电源发电成本微增率曲线
图8展示了当下垂系数k从10增加到200时小信号模型主导特征值的变化。由图8可知,在较广的下垂系数变化范围内,主导特征值始终落在s域的左半平面,可以保证直流微网稳定运行,随着下垂系数k的增大,系统稳定性先逐渐改善,随后逐渐减弱。值得说明的是,下垂系数除了影响系统稳定性外,还会影响直流母线电压变化的暂态性能,经过权衡,最终在该算例中选取k=60。同样,通过小干扰稳定性分析可选取等微增率控制参数T=0.1,w=0.05。

图8 分布式电源发电成本微增率曲线
4 算例分析
为了验证本文所提等微增率下垂控制方法的有效性,在RTLAB和Matlab/Simulink中搭建如图6所示的直流微网模型,直流母线电压为600V,三台分布式电源接入直流微网分担负荷,发电成本微增率曲线如图7所示。
4.1 下垂控制方法调控性能分析
在该算例场景中,设初始负荷为60kW,在t=1s时,负荷下降至45kW;在t=2s时,负荷增加至65kW;在t=3s时,负荷进一步增加至73kW;在t=4s时,负荷降至60kW。图9和图10分别展示了传统下垂控制和等微增率下垂控制方法下直流母线电压的变化。
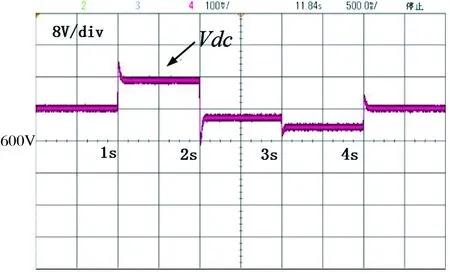
图9 传统下垂控制

图10 λ-V下垂控制
由图9和图10对比可知,传统下垂控制中,直流母线稳态电压偏差无法避免,且该偏差反比于负荷功率波动。而等微增率下垂控制可以完全消除直流母线稳态电压偏差。电压变化暂态过程分为两个阶段,在t=1s时,随着负荷下降,直流母线电压升高至607V,0.1s后开始电压恢复过程,经过0.3s,电压恢复至额定值,总电压恢复时间为T2=0.4s,与第一节理论分析相吻合。其余场景电压变化过程与之类似。
为进一步验证负荷快速波动时等微增率下垂控制的稳定性,考虑负荷波动如图11所示,负荷变化时间间隔为0.1s。图12和图13分别展示了三台分布式电源的发电微增率变化曲线和直流母线电压变化曲线。
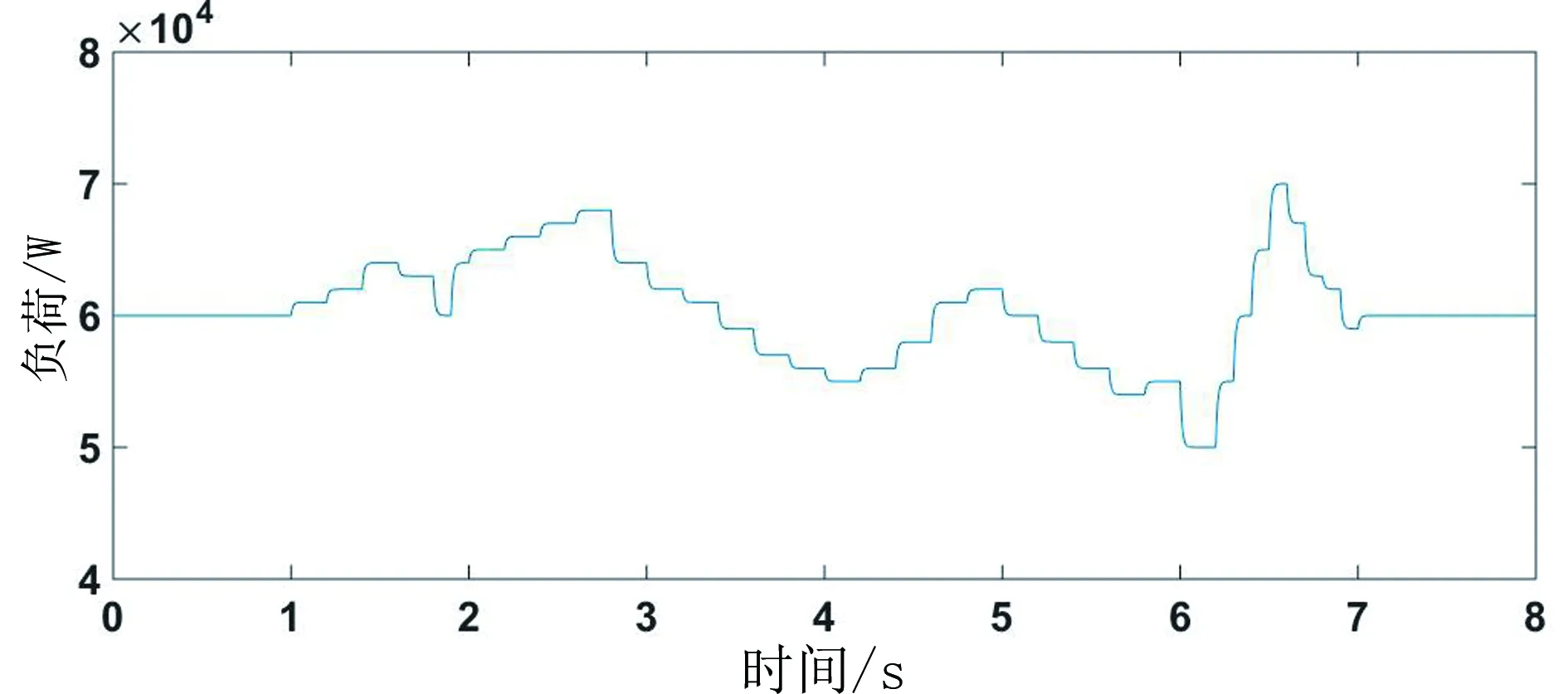
图11 负荷变化

图12 发电成本微增率变化
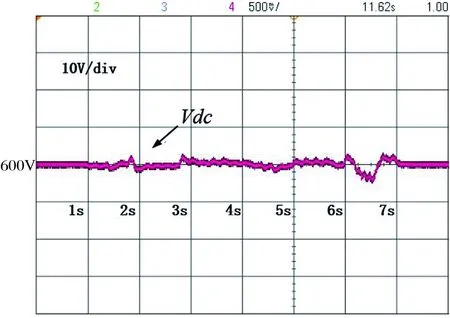
图13 直流母线电压变化
由图12和图13可知,各分布式电源可以在保证等微增率运行的同时快速追踪负荷变化,实现负荷功率的经济分担。直流母线电压在负荷波动时始终处于安全运行域范围内,且当t=7s时可以重新恢复至额定值600V。综上,本文提出的等微增率下垂控制方法在负荷快速变化时具有良好的动态性能。
4.2 即插即用策略有效性分析
在该算例场景中,设初始负荷为50kW,在t=1s时,DG1断开,由DG2和DG3为负荷供电;在t=2s时,DG1重新接入直流微网。图14和图15分别展示了分散式即插即用和分布式即插即用策略下各台分布式电源的发电成本微增率曲线。由图可知,分散式即插即用策略由于存在母线电压检测延迟,因而在t=2s DG1刚并入微网的时刻无法维持等微增率运行,同时在t=2.5s控制切换过程中存在微小的功率扰动。而分布式即插即用策略以增加通信成本为代价,在DG1断开及接入时,各并网电源均能保持等微增率运行,且功率曲线更加平滑,产生的功率扰动较小。

图14 分散式即插即用成本微增率变化
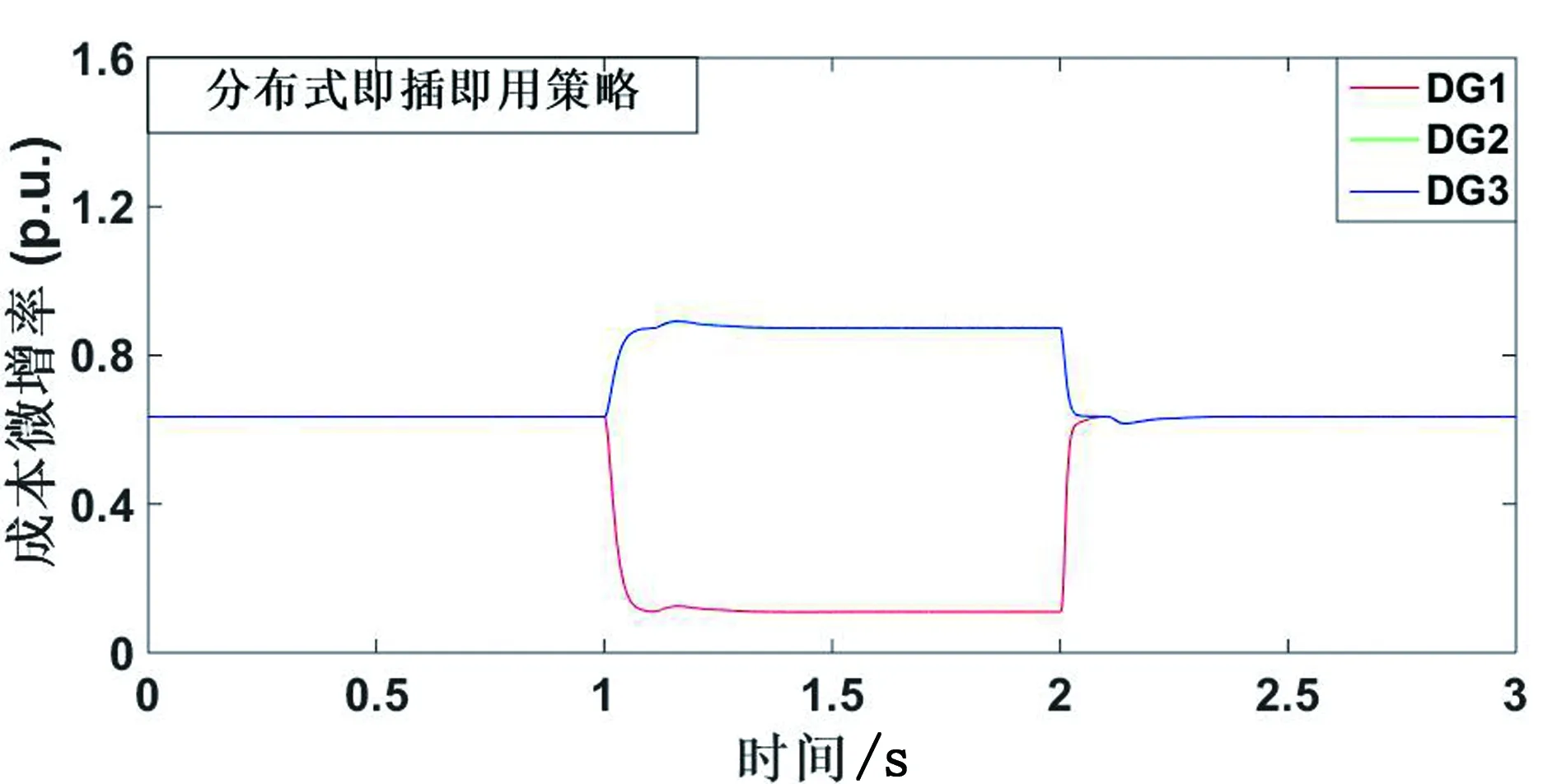
图15 分布式即插即用成本微增率变化
5 结论
本文提出了一种适用于孤岛直流微网的等微增率下垂控制方法,以提高直流母线电压质量和微网的运行经济性。通过在下垂控制中增加成本微增率的时滞前馈环节,该控制方法可以在消除直流母线稳态电压偏差的同时保证各分布式电源等微增率运行,以实现发电成本最优。此外,为了提高系统的运行可靠性及可拓展性,提出了两种即插即用控制策略,分布式即插即用策略与分散式即插即用策略相比,以增加通信成本为代价,可以有效改善分布式电源接入与退出时系统的暂态响应性能。

