改进Mein-Larson模型的花岗岩残积土边坡降雨入渗研究

郭志峰，宿文姬，张 伟，郑志文，魏平新

（1.华南理工大学土木与交通学院，广州 510640，2.广东省地质环境监测总站，广州 510510）

0 引言

降雨是滑坡灾害中最为突出的一个致灾因素[1]，雨水下渗过程中，湿润锋面也同步向下推进，导致边坡性能软化，安全系数逐步降低。在研究湿润锋向下发展的运移规律中，多是将土体的初始含水率简化为与标高成正比的线性分布，而较少考虑土体中初始含水率非线性分布对于湿润锋运移规律的影响，而实际上自然界中土体初始含水率的分布通常都是非线性的，充分考虑这一差异对于准确描述湿润锋运移规律是十分重要的，也关系到边坡的稳定性。

传统Green-Ampt 降雨入渗模型以湿润锋为界，将土层分为两个区域，以上为饱和层，以下为初始层，假定两层土体含水率都均匀分布，而Mein-Larson 入渗模型则在Green-Ampt 入渗模型的基础上考虑了坡面倾角和弱降雨—自由入渗的情况，适用性更广。但实际的入渗过程中，土体的初始含水率分布并不均匀，基于此，众多学者对于降雨入渗模型都进行了部分改进，以期能够获得适应性和准确性更强的入渗模型。如马娟娟等[2]基于Green-Ampt 入渗模型考虑地表积水厚度变化，推导湿润锋入渗深度与时间的变化关系；彭振阳等[3]基于土体分层假定对Green-Ampt 入渗模型进行改进，推导出湿润锋椭圆形向下推进时的入渗深度-时间变化规律，并基于Richards 方程的土壤水运动模型进行验证；唐扬等[4]考虑初始含水率的线性分布，针对Mein-Larson 入渗模型进行改进，得出一种新的降雨模型，并与有限元法结果进行对比，证实了土体初始含水率的分布影响到湿润锋的下移。杜京房等[5]采用修正Mein-Larson 入渗模型进行干湿循环与降雨双重因素影响下的边坡稳定性研究；陈俊成[6]基于Mein-Larson 入渗模型，假定土体初始含水率呈反比例分布，推导出强降雨和弱降雨阶段的湿润锋入渗深度-时间变化关系，并针对改进模型进行数值模拟验证与现场试验验证。

对于土体初始含水率呈指数型分布的研究还较少，综上所述，本文将提出一种新的指数型函数来表征初始含水率分布，对Mein-Larson 模型进行改进，推导湿润锋入渗深度随时间的变化规律，并针对改进模型进行对比验证。

1 Mein-Larson入渗模型及改进

1.1 传统Mein-Larson入渗模型

20 世纪中叶，Mein 和Larson 两位学者针对传统G-A 模型未考虑边坡倾角和弱降雨—自由入渗的不足进行推导，提出了Mein-Larson 入渗模型（以下简称M-L 入渗模型）。它主要建立在以下几个假定的前提下：①边坡为均质土体；②雨水入渗过程中，土体分为湿润层和初始层两层，两层的含水率均匀分布，初始层含水率为初始体积含水率；③水分的传导方向为垂直坡面向下即湿润锋面垂直坡面向下平行推进；④湿润锋面处基质吸力不变，为常量。

Mein-Larson 入渗模型如图1 所示，先分析弱降雨—自由入渗阶段即降雨强度小于土体入渗率阶段，此时湿润锋以上的含水率为湿润含水率θw，湿润锋以下的含水率为土体的初始含水率θi，坡面倾角为β，坡面上z*方向的入渗率为i，以坡面作为参考面，以沿坡面垂直向下作为z*轴正方向，θ 轴为土体的含水率轴，根据达西定律可得式：

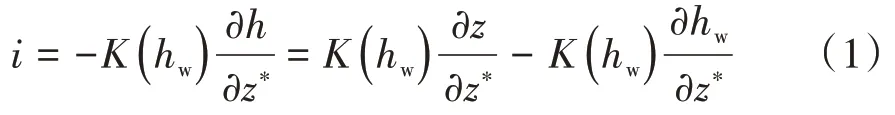
式（1）中：hw为压力水头；K( )hw为与压力水头hw相关的土体渗透系数。

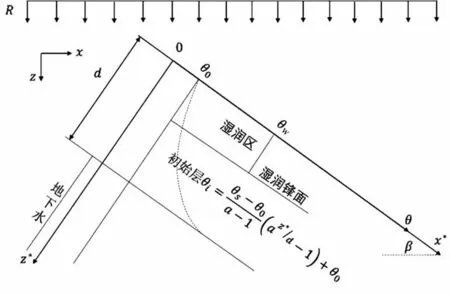
图1 Mein-Larson入渗模型（自由入渗阶段）Fig.1 Mein-Larson infiltration model（free infiltration stage）

根据坐标的转换关系，可得式：

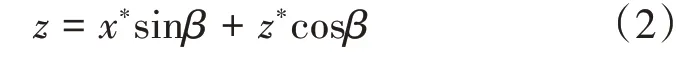
联立式和式，整理可得：

图2 Mein-Larson入渗模型（有压入渗阶段）Fig.2 Mein-Larson infiltration model（with pressure infiltration stage）

1.2 M-L入渗模型的改进

传统M-L 入渗模型假设土体初始含水率均匀分布，这显然与自然土体中的含水率分布相差甚远，难以准确描述土体中水分的分布情况，且为了简化研究，将湿润锋的发展规律假设为直线均匀推进，与实际情况不符。本文针对M-L 入渗模型存在的上述不足，基于分层假定引入一种新的指数型分布函数表征土体的含水率对其进行改进。

1.2.1 土体含水率分布函数修正

假定土体初始含水率分布函数为指数型分布，湿润层内土体的含水率为湿润含水率θw，初始层内的土体含水率为θi，改进模型如图3 所示，两层区域的土体含水率分布函数如式（22）和式（23）：

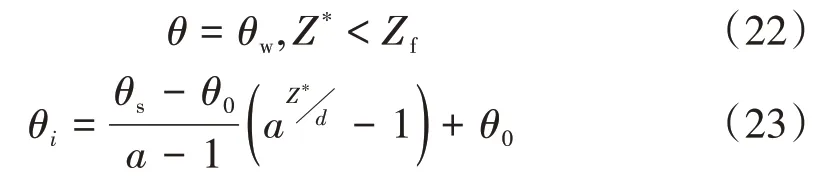
式（23）中，Zf为湿润锋的入渗深度（m）；Z*为土体深度（m）；θs、θw分别为土体饱和含水率与湿润层土体含水率；d 为地下水埋深（m）；θ0为土体含水率拟合参数，物理意义为表层土体含水率；a 为土体含水率拟合参数。

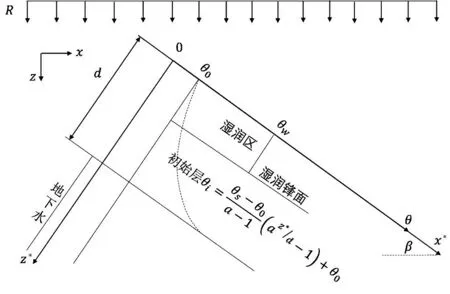
图3 改进M-L降雨入渗模型Fig.3 Improved M-L rainfall infiltration model

1.3 改进Mein-Larson入渗模型的建立

本文提出的改进降雨入渗模型分为弱降雨和强降雨两个情况分别对应自由入渗和有压入渗，基于上述的假定来推导湿润锋入渗深度Zf与时间t的关系，先分析弱降雨—自由入渗阶段，改进降雨入渗模型如上图3所示，由于此阶段降雨强度恒小于土体入渗率，此时坡体法向的入渗率即为降雨强度在此方向的分量，表达式见式（26）。

对式（28）进行积分运算，并带入初始条件Zf|t=0= 0，积分可得：

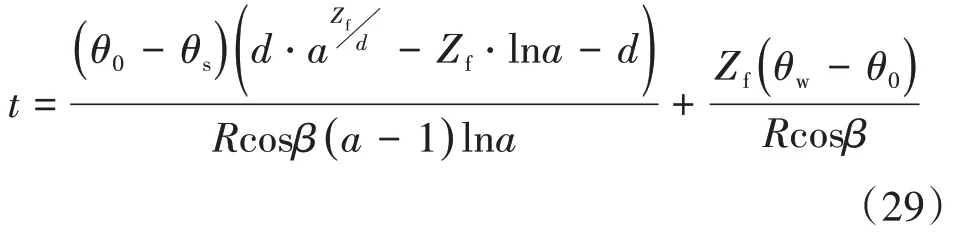
式（29）即为改进之后，自由入渗阶段湿润锋入渗深度随时间增长的变化关系式。

再来推导强降雨—有压入渗阶段，湿润锋随时间的变化关系式。此阶段降雨强度恒大于土体入渗率，由土体入渗能力控制水分入渗，由达西定律可以得知：

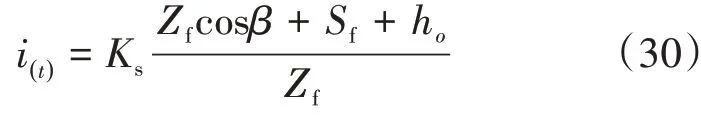
考虑边坡入渗时间很长即形成稳定的坡面径流时的情况或坡面径流高度较小时，此时可以将ho忽略不计。

同理，将累计入渗总量I对时间t求导，即为土体入渗率i(t)，联立式（27）及式（30），化简整理可得：

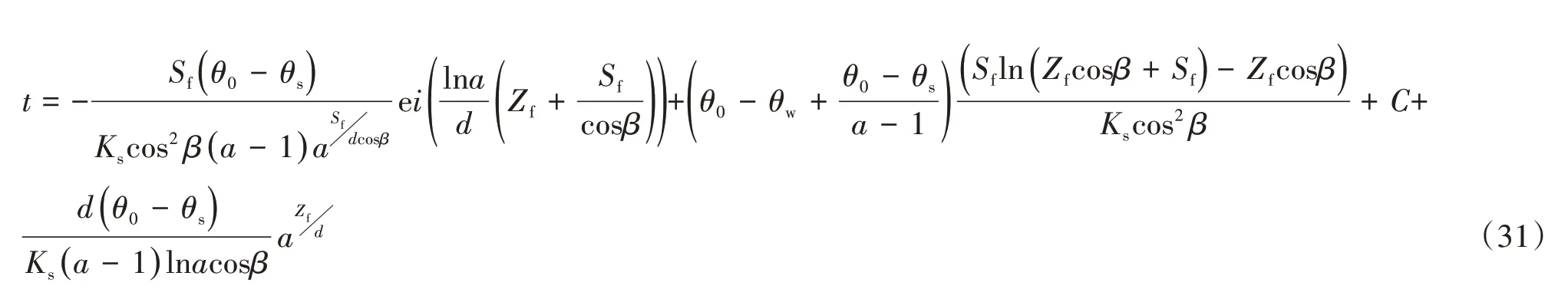
式（31）中C 为积分常数，代入初始条件 |Zft=0= 0便可求得。式（31）即为改进之后，有压入渗阶段湿润锋入渗深度随时间增长的变化关系式。

当降雨强度略大于土体的饱和入渗率时，降雨前期会发生自由入渗，经过积水时刻后，发生有压入渗，此时的水分入渗经过自由入渗到有压入渗的转化。现进行此入渗过程中湿润锋入渗深度随时间的变化关系的推导。

两个阶段的转化时刻即为坡面开始积水时刻，设为tp，累计入渗雨量设为Ip，湿润锋入渗深度设为Zp，此时，土体入渗率在数值上就等于降雨强度在垂直坡面方向的分量。

联立式（26）及式（30），可求解得到Zp如下所示：

坡面开始积水时刻的累计入渗雨量Ip表达式如式（33）：

当t ＜tp（即自由入渗阶段）时，湿润锋入渗深度随时间的变化关系表达式同式（29）。

当t ≥tp（即有压入渗阶段）时，湿润锋入渗深度随时间的变化关系表达式需要对式（31）进行修正，式（31）是以t = 0 作为入渗的开始时刻点，而实际上的有压入渗阶段发生在积水点之后也即t =tp之后的阶段，并考虑将初始条件 |Zft = tp= Zp，则修正之后的表达式（37）如下式所示，其中累计入渗总量见式（25）：

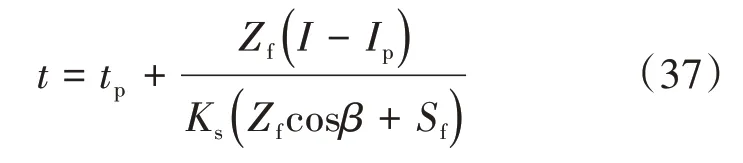
式（29）及式（37）即为降雨强度略大于土体饱和入渗率时，全降雨阶段的湿润锋入渗深度随时间的变化关系表达式。

2 改进M-L入渗模型的验证

2.1 试验简介

本文选取华南地区花岗岩残积土边坡来进行改进M-L 模型的试验验证。该试验边坡坡高10 m，坡长20 m，坡角为30°，地下水埋深7 m，其基质吸力水头取为8.14×10-2m，土体的具体参数列于下表1所示。

表1 花岗岩残积土计算参数Table 1 Calculation parameters of granite residual soil

表中：θr为土体残余含水率；θs为土体饱和含水率；Ks为土体饱和渗透系数(m·d-1)；α、n 为土体特征曲线拟合参数。

2.2 改进后的土体初始含水率分布验证

根据该边坡在不同深度处的初始含水率数据，利用式（24）进行拟合，该拟合结果见图4。

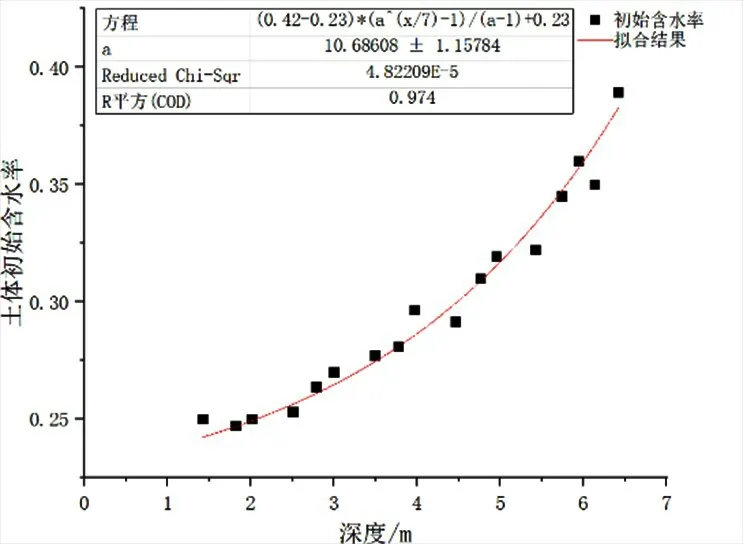
图4 土体初始含水率拟合结果Fig.4 Fitting results of soil initial moisture content

由上图可知，R2=0.974拟合优度接近于1，拟合效果具有可信度，依此便可以得到土体初始含水率随深度的变化规律曲线，具体表达式见下式（38）。

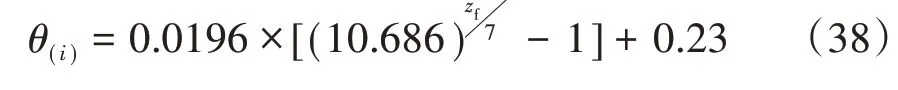
2.3 湿润锋深度验证

本文改进M-L 模型主要有弱降雨—自由入渗阶段和强降雨—有压入渗阶段，依据该地区降雨数据，针对本试验边坡模型选取两个降雨强度，分别为R = 8.0和R = 50.8，另外在降雨强度略大于土体饱和入渗率时，存在一个弱降雨向强降雨转化的阶段，故增加一个降雨强度为R = 26.0，进行验证。水分在入渗过程中，湿润锋上部的土体体积含水率通常不饱和，故此湿润锋上部土体体积含水率取为θw= 0.9,θs= 0.378，将a = 10.686，d =7m，β = 30o，θ0= 0.23，R = 0.192 代入式（29），便可以求得自由入渗阶段降雨强度为8.0 的湿润锋入渗深度随时间的变化曲线，绘出该曲线如图5 所示。将R = 0.624，Sf= 0.0814 m，Ks= 0.594 与上述参数分别代入式（34）、式（36），便可求得Ip=0.2643 m，tp= 0.489 d，将上述数据分别代入式（29）及 式（37）便可以求得降雨强度R = 26.0 时，在整个降雨入渗过程中，湿润锋入渗深度随时间的变化曲线。绘出该湿润锋入渗深度-时间变化曲线如图6 所示。将R = 1.22 与上述参数代入式（37），便可求得降雨强度R = 50.8 时，在整个降雨入渗过程中，湿润锋入渗深度随时间的变化曲线。绘出该湿润锋入渗深度-时间变化曲线如图7所示。

文献[6]中的改进降雨入渗模型是基于M-L 模型，考虑倾角和初始含水率呈反比例函数分布推导得出的，该反比例型初始含水率分布见式（39），式（40）为自由入渗和有压入渗两个阶段的表达式，本文将其作为对比模型1。文献[7]中的改进降雨入渗模型则是基于G-A 模型，考虑倾角的影响推导得出的，式（41）为该模型的表达式，本文将其作为对比模型2。式（40）及式（41）中各物理量意义同本文。

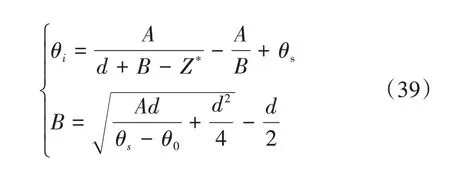
式（39）中：A、B 为拟合参数；d 为地下水埋深（m）；θ0为坡面表层土初始含水率；θs为饱和含水率。针对本试验边坡，各参数分别取值为A =0.8306，B = 3.0709，d = 7 m、θ0= 0.232，θs= 0.42，h0= 0。式（41）中Kw取为土体的饱和渗透系数。将上述两个模型得出的解以及本文M-L 改进模型的解与数值解进行对比分析，分析结果列于表2。

表2 不同降雨条件下湿润锋入渗深度随时间的变化关系Table 2 Variation of wetting front infiltration depth with time under different rainfall conditions

工况2 中：本文改进模型积水时刻为0.536 d，此时湿润锋入渗深度2.183 m；对比模型1 积水时刻为0.722 d，湿润锋入渗深度3.523 m；对比模型2积水时刻为0.569 d，入渗深度2.182 m。

由上表可以看出，本文改进降雨入渗M-L 模型的计算结果与模型1、模型2 及数值解均具有较好的一致性，按照本文的模型来考虑初始含水率非线性的指数型分布是可靠的。分析上表，即可看出在工况1 和工况3 两种情况下，本文提出的模型计算结果与模型-1 的计算结果相比，湿润锋入渗深度较小；在工况-2 情况下，本文的改进模型计算结果较模型-1 的计算结果相比较大，这主要的原因在于：模型-1 中的初始含水率分布是假定为均匀分布与实际土体中含水率分布的不均匀所导致的。这得出的结论与文献[6]得到的结论也是一致的。由下图5 与图6 对比分析可以看出模型-2 的计算结果与本文模型变化规律是大致相同的，这主要是因为两种模型都是基于指数型初始含水率的分布形式推导得出的。

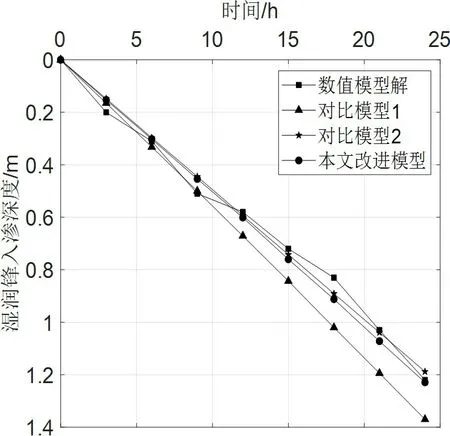
图5 工况1湿润锋-时间变化曲线Fig.5 Wetting front-time curve of working condition 1

图6 工况2湿润锋-时间变化曲线Fig.6 Wetting front-time curve of working condition 2

图7 工况3湿润锋-时间变化曲线Fig.7 Wetting front-time curve of working condition 3

对比上述三图可以得出：在弱降雨-自由入渗阶段，湿润锋的入渗规律随时间基本上呈线性变化的，这大致上有两方面的原因：其一是该阶段的入渗主要由降雨强度控制；其二是降雨强度过小，累积入渗量过小，不足以推进湿润锋向深处发展。在自由入渗—有压入渗转化阶段，本文改进模型的积水时刻较对比模型1早了4.5 h，在工程上来讲是更偏于安全的，完全可以接受。而对比模型2 与其他三个模型的解在同一时刻，湿润锋入渗深度差值较大，吻合度较低，主要是因为对比模型2 将初始含水率假定为均匀分布，过于依赖初始含水率的取值，敏感性太大，这充分说明初始含水率非线性分布的必要性。积水时刻之后，本阶段大致以湿润锋入渗深度为4 m 时为界，变化曲线逐渐呈现出指数变化的形式，其原因大致有两个，其一是越靠近地下水位，其土体初始含水率便越大，入渗所需的雨量便越小，则在降雨强度不变的条件下，湿润锋的入渗速率便越快。其二是坡面上方形成径流，导致湿润锋下渗的动力增加，下渗的速率加快。同理，在强降雨-有压入渗阶段，大致以3.5 m为界，变化曲线呈现指数变化规律，也可由此解释。

3 结论与建议

（1）本文提出了一种新的基于指数型的土体初始含水率分布拟合函数，用来研究边坡在降雨过程中，湿润锋入渗深度随时间的变化规律，通过数值模拟与实际土体边坡初始含水率分布验证了该拟合函数的准确性与适用性。

（2）通过对比前人提出的两种入渗模型和数值模型解，发现本文改进入渗模型与数值模型的拟合效果相较前人提出的两种模型效果更佳，且与前人提出的初始含水率呈反比例分布的模型具有较好的一致性，极大消除M-L 模型考虑初始含水率线性分布的不足，本文改进M-L 入渗模型较前人模型出现坡面积水的时刻早4.5 h，积水时刻之后的湿润锋入渗深度-时间变化曲线呈现指数型发展的规律，与数值模型解具有一致性，说明了本文提出的改进模型比前人提出的两种模型效果更佳。