数据驱动下供应链系统变更自适应预测控制
刘炜 恒庆海 李庆奎
北京信息科技大学自动化学院,北京 100101
0 前言
供应链系统是由供应商、制造商、分销商和零售商组成的复杂网络系统,具有原材料采购、材料转化为中间产品和成品以及成品分销的功能,并通过控制信息流和物流[1]传递给客户。目前,大多数的动态供应链系统采用机理建模[2]的方式,利用物料平衡等原理对供应链系统进行建模,然后从控制工程的角度设计控制策略,改善系统的性能,抑制不确定需求对供应链系统的影响,以达到更加高效的供应链管理和决策。事实上,复杂供应链系统由于节点多,运行时间尺度不一,以及模态混杂,机理建模通常不易实现,而利用供应链运作过程中产生的数据进行建模比机理建模更加贴近实际。在无法获取系统内部参数的条件下,子空间辨识方法可以利用输入输出数据获得预测矩阵,这种直接数据驱动方法在学术界和工业界已有使用,WOODLEY B R等人[3]将该子空间辨识方法进行扩展并应用到了H∞控制中,其设计方法更方便扩展到自适应控制算法。GHASEMI H等人[4]的研究表明,子空间预估器可以对系统未来状态进行预测,满足预测控制的要求。KADALI R等人[5]提出了利用预估器设计预测控制的算法。另一方面,对于供应链系统为了降低企业成本,优化生产策略,在应对客户需求的不确定性下出现的库存积压以及供应链中生产环节的变更造成的库存波动,许多学者[6-7]采用预测控制策略进行生产库存的决策。
预测控制来源于工业应用[8],在化工、航天等领域均有涉及。由于其对建模精确程度要求不高,并且在控制周期内采用滚动优化策略,故对于系统模型失配和干扰抑制的性能较好,所以在供应链系统中也常使用。BOSE S等人[9]研究了预测控制在供应链系统中的应用,结果表明,这种滚动优化的策略在供应链系统的优化决策中有突出的优势。PEREA-LÓPEZ E等人[10]采用模型预测控制策略,寻找多产品供应链中利润最大化的最优决策变量,在集中管理和分散管理方式下均取得了较好的效果。
传统动态供应链系统的研究一般是在基于机理建模下讨论末端不确定用户需求对供应链系统各级节点的影响[11-12]。然而,由于突发事件或各种因素的影响造成供应链系统变更是不可避免的。研究基于变更设计的供应链系统分析、控制及预测问题,具有重要的现实意义,尤其在新冠疫情及贸易争端背景下,全球供应链系统受到重要影响,有些处于中断或阻塞状态,对经济平稳运行产生巨大影响。众多研究者从不同角度开展相关研究,如:QI X等人[13]研究了静态方式下存在需求中断时供应链协调的条件;HEARNSHAW E J S等人[14]的研究表明,供应链系统变更首先会影响该节点中的设备,其次,由于供应链的级联特性,某一节点的变更会使得该供应链中的其他设备也受到影响;BLACKHURST J V等人[15]指出由于供应链之间的关联性、全球性,所以在中断等突发事件的影响下会破坏人员、货物、信息的流动而使供应链的成本增加。为解决上述问题,ZHAO K等人[16]使用拓扑分析等技术提高了供应链网络的鲁棒性;BEHZADI G等人[17]利用鲁棒优化技术,得到了期望利润和风险为目标的风险规避解。上述研究大多基于供应链管理角度研究系统变更造成的不良影响并未考虑各生产节点的动态,本文旨在从工程控制论的角度设计控制器来进行生产决策,利用数据驱动方法可以很方便地将供应链系统变更问题建模为系统内部参数的变化,从而避免由于系统内节点变更导致对供应链系统的不良影响。
本文借鉴上述文献的思想,从工程控制论的角度,针对动态供应链系统中节点发生变更的情况,提出了一种基于数据驱动的自适应预测控制方法。首先,为更加符合实际供应链运行状况,利用数据驱动的方法建立供应链系统的子空间预估模型,由于运行过程中系统发生变更,故引入滑动窗口机制对系统进行在线辨识,利用异常数据检查机制更新预估器矩阵;其次,将子空间预估器作为预测模型,利用预估矩阵参数设计自适应预测控制器,通过滚动优化和反馈校正机制,进一步求得多级供应链系统在运作过程中发生内部节点变更状况下的库存控制策略;最后,以三节点生产—库存供应链系统为例,验证所提出的方法。在仿真部分,验证了基于数据建模的准确性和供应链系统在自适应预测控制的生产策略下,其在内部节点发生变更前后库存水平的波动状况,仿真结果表明该方法的鲁棒性和有效性。
1 问题描述
如图1所示的多级供应链系统,其中,xi表示下游节点给上游节点的订单量;ui表示节点i的生产量;yi表示每个生产节点的库存数量。假设,每个节点的yi和ui均可获得,且在理想状态下不考虑运输途中的损失,根据文献[18],供应链系统动态可以用差分方程来表达,当多级供应链中的某一个节点或者几个节点由于突发原因产生变更时,必然造成系统内部参数的变化,这些变化最终会反映到系统的输入输出数据上。本文采用数据驱动的思想对供应链系统进行在线建模,利用预测控制求解生产策略,从而使系统在发生变更后仍然能够稳定运行。

由于多级供应链系统末端用户需求一般视作不确定的,且与生产量之间是相互独立的,采用POMOSEP法对上述多级供应链系统进行辨识。基于数据驱动的供应链系统可以用下式描述:

其中,(k) ∈Rm——各级理想生产量;
(k)∈Rl——理想状态下各级库存量;
f(·) ——未知函数;
θ(k) ——时变参数用来刻画系统的变更情况,采用有限时域的滑动窗口在线辨识方法,递推更新模型。在进行闭环辨识的过程中会有各种干扰,定义输入输出信号测量模型:

其中,ω∈Rl、v∈Rm分别为各级库存量的测量噪声和生产量的测量噪声,ω和v是有界的且与过去的控制量u不相关。子空间预估器采用如下不确定形式描述:
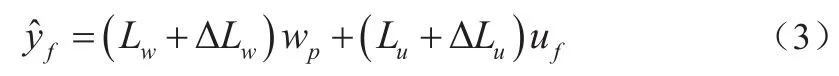
uf=节点未来的生产量;
k——当前采样时刻,每个元素均为列向量;
wp=过去库存水平和生产量的输入输出矩阵;
Np——预测时域;
Nc——控制时域。
公式(3)表征了各级生产量与各级库存量之间的关系,模型参数可直接作为控制器的设计参数,ΔLw和ΔLu表示模型的不确定性。
2 子空间辨识与预测控制
2.1 自适应子空间辨识与异常数据检查策略
构造输入量U的Hankel矩阵如下:

其中,p、f——“过去”和“未来”;
Up——系统“过去”的输入;
Uf——系统“未来”的输入。

其中,L=[L,L]为子空间矩阵,满足L1∈R(l×N)×((l+m)×N),
12分别表示状态和确定性输入子空间预估器矩阵。
公元618年,唐国公李渊长安称帝,建立了繁荣的大唐帝国,从此中国封建社会进入了最为强盛的时期。一个民族音乐文化的发展壮大,有的时候需要几个世纪的文化沉淀,而就在唐朝建立初期,这个漫长的音乐文化沉淀已悄然开始。它融会贯通、博采众长,造就出了历史上空前强盛的局面,为中国古代音乐文化做出了积极的贡献。唐代的音乐机构主要分由政府管辖和宫廷管辖两个不同的体系,其中太常寺是唐代最高的行政机构,大乐署、鼓吹署隶属于太常寺,属于政府管理的音乐机构,监管雅乐与俗乐。教坊和梨园则隶属于宫廷管辖。
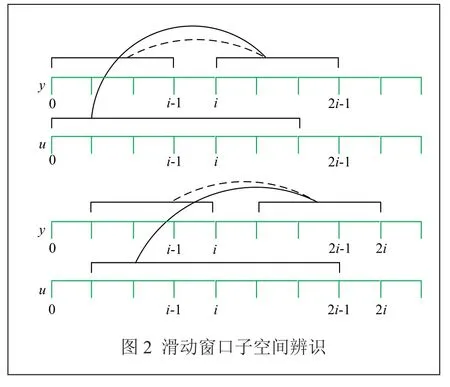
对于式(1)的系统,设计长度为n的滑动窗口方法在线更新用于计算子空间预估器矩阵的数据,并且在每个采样时刻利用递推方法更新一次数据集,从而实现预测模型的在线求解。
设Ξ∈R4N(m+l)×j为k时刻的输入输出Hankel矩阵:
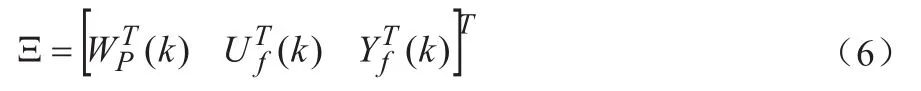
其中,Wp(k)、Uf(k)和Yf(k)分别为闭环系统采集到的过去生产量和库存水平数据矩阵、未来生产量数据矩阵和库存水平数据矩阵。将Ξ最左列的[19]数据定义为在k+1采样时刻,将一组新的生产量和库存水平数据定义为,其 中,
在k+1采样时刻的输入输出Hankel矩阵Ψ为:

其中,Wp(k+1)、Uf(k+1)和Yf(k+1)与Wp(k)、Uf(k)和Yf(k)的定义类似。
为了保证滚动窗口大小固定,须将ξ从Ξ中移除,并将ζ添加到Ξ中,因此得到关系式 [Ξ :ζ]= [ξ: Ψ],进一步有 [Ξ :ζ][Ξ :ζ]T= [ξ: Ψ][ξ: Ψ]T,对该式分解得到:

则k+1时刻的输入输出Hankel矩阵Ψ的QR分解结果:
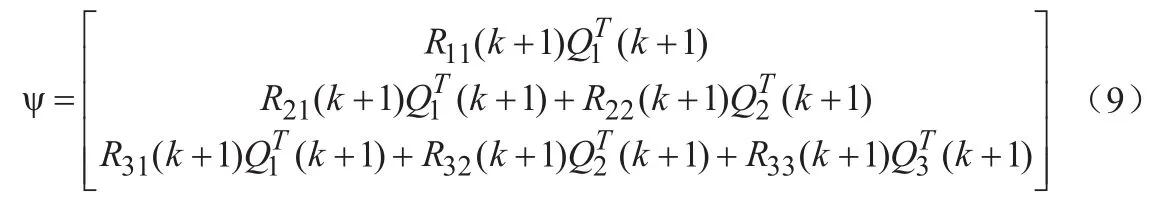
同理,对k时刻的Ξ进行上述操作,由上述定义和式(8)可分别求得ζζT和ξξT,进一步可得预估器矩阵R(k+1)中:
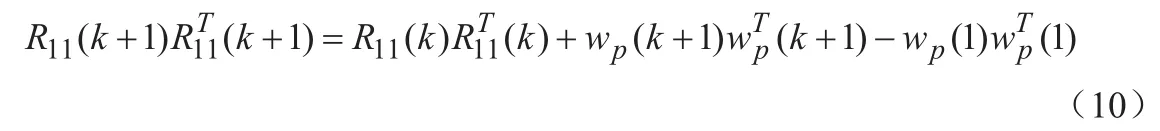
故:
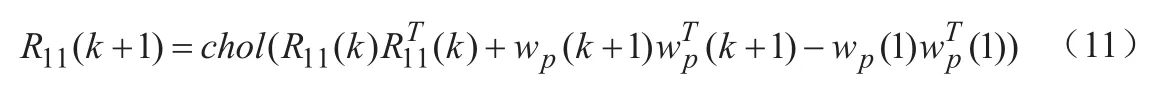
其中,chol(·)为Cholesky分解。要得到子空间预估器矩阵,需先求R21(k+1)、R22(k+1)和R32(k+1)。

同理,利用式(8)与Cholesky分解可分别求得R31(k+1)、R22(k+1)和R32(k+1)。

其中, † 表示伪逆矩阵,通过奇异值分解得到,式(3)表示的子空间预估器模型中,Lw=L1,Lu为L2的前l×Nu列元素。
2.2 异常数据检查策略
由于动态供应链系统的运作过程存在用户的不确定性需求,各级库存量的测量过程难免存在噪声影响,这些因素会降低滑动窗口自适应策略的辨识精度。采用一次预测误差的数据检查策略来消除异常数据对在线辨识过程的影响[19-20]。
计算数据更新前的预测误差:

yk+1——k+1时刻的实测值。

在下一采样时刻,重复上面的异常数据检查策略。
通过滑动窗口自适应机制与异常数据检查策略有ΔLw→0,ΔLu→0,故式(3)可以转化为:

2.3 控制器设计与自适应预测算法
在预测控制设计中,定义性能指标函数为:

rf——参考库存水平;
uf——控制量;
Q≥0,R>0。
将上述滑动窗口自适应辨识策略与预测控制相结合,则自适应预测控制问题可以描述为求解如下的优化问题,即:

将式(17)带入式(18)可得:
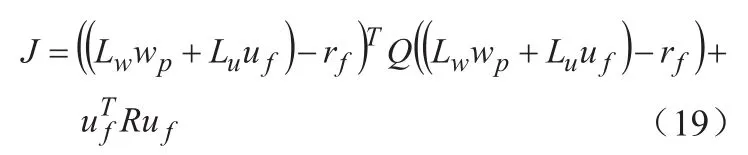

系统在每个采样时刻重新计算式(19)的优化问题,得到最优控制序列uf,取最优控制序列的第一项作为当前的控制率施加到控制系统中。
自适应预测控制算法步骤:
(1)采集多级供应链系统中各级生产量与库存量,构造闭环供应链系统的Hankel矩阵;
(2)在采样时刻k,利用QR分解计算初始Lw和Lu;
(4)利用式(20)计算最优预测控制序列uk,并施加到系统中;
(5)在采样时刻k+1,采集到新的系统数据时,执行2.2节中的异常数据检查策略,当新数据异常时,保持uk,否则,进行如下步骤:
(6)构造新的生产量与库存水平的Hankel矩阵Ψ,通过式(11)~(13)计算R矩阵;
(7)进行异常数据检查,决定是否更新R矩阵,通过步骤(3)和步骤(4)计算预测输出和最优预测控制序列uk,然后返回步骤(5)进行异常数据判断。
3 仿真分析
以三节点生产—库存供应链系统[9]为例,验证上述算法的有效性,其中,yi(s)为供应链系统的3个生产环节的库存水平;ui(s)为供应链系统的3个生产环节的出货量,其中,θi为生产运输延迟,αi为损耗系数。

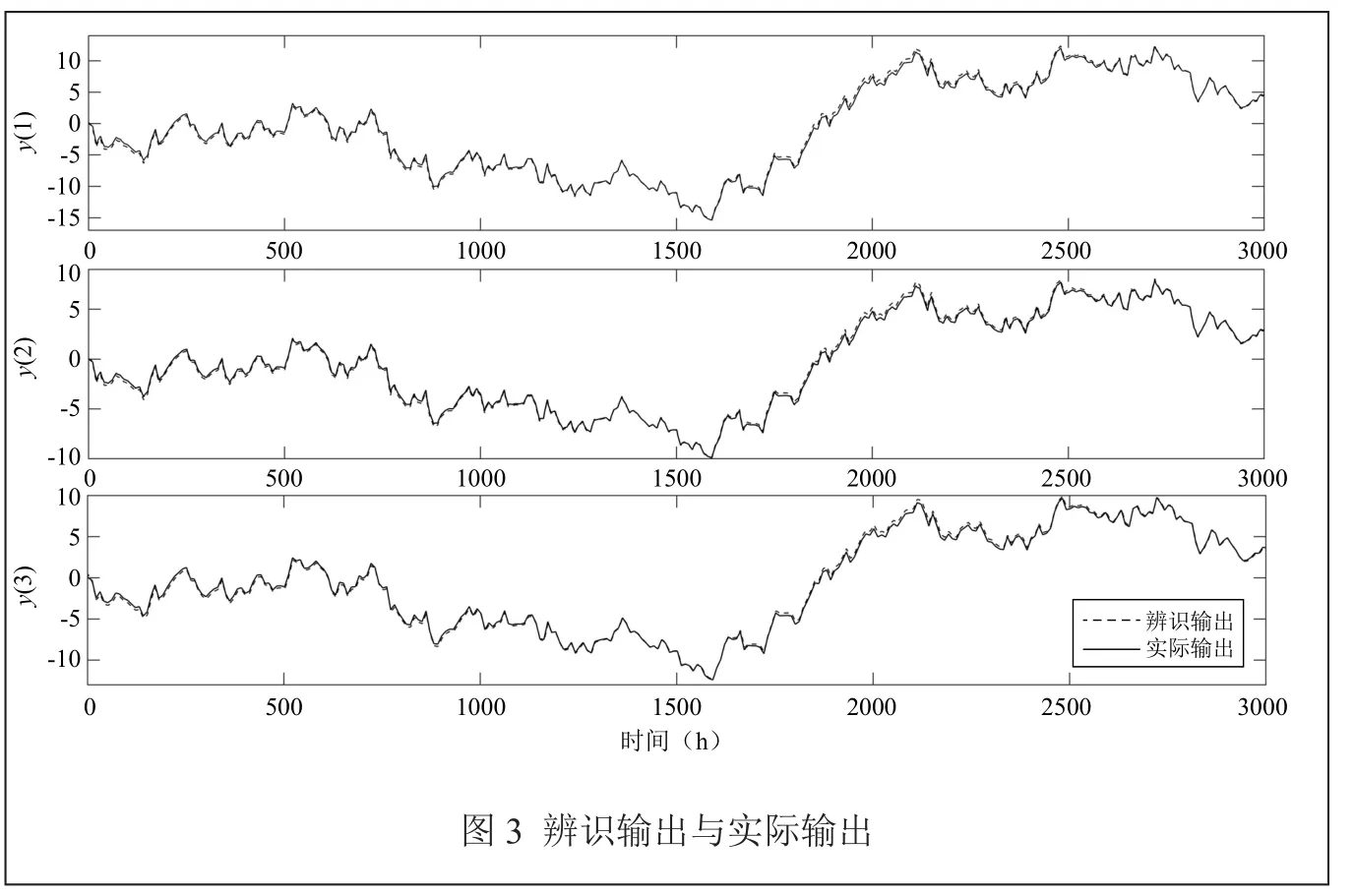
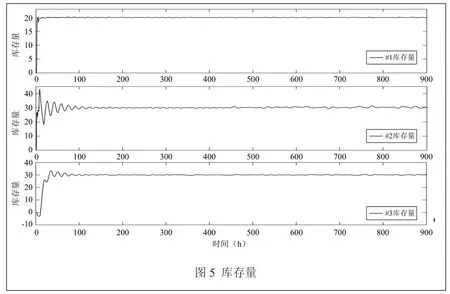
假设三节点生产—库存供应链系统在t=450时,由于突发事件造成生产环节的第二环节发生变更,其延迟系数变为θ2′=3。采用自适应预测控制策略进行生产决策,设置控制时域Nc=40,预测时域Np=60,不确定用户需求满足正态分布(μ,σ),其中,μ=0,σ=0.01,库存水平设定值为一号仓库20,二号仓库30,三号仓库30。仿真结果表明,在上述用户需求下,采用自适应预测控制策略可以使得库存水平维持在设定值范围内。在t=450时,二号节点仓库发生变更,可以看出,库存水平虽然波动,但仍在允许范围,仿真结果如图5所示。
5 结束语
本文对多级供应链系统在正常生产运作过程中某生产环节发生变更的情况下,从控制理论的角度提出了基于数据驱动自适应预测控制的生产-库存控制策略。为了更符合实际供应链系统的运行状况,文中采用数据驱动的方式对系统进行在线辨识,将生产环节的变更问题建模为系统内部的可变参数。为增加控制器的鲁棒性,利用滑动窗口子空间线辨识方法,结合异常数据检测机制更新预估器矩阵建立系统的预测模型,将子空间预估器参数与预测控制相结合,利用滚动优化与反馈校正机制,设计了自适应预测控制器在线求解最优控制率,最后在仿真部分利用一个三节点生产—库存供应链系统验证了所提方法能够在发生系统变更的情况下,将库存水平维持在给定值允许的误差范围内,表明该方法的鲁棒性和有效性。