基于低Q 腔的无集体弛豫量子信息处理

刘阿鹏，郭 奇

(1.山西工程技术学院 基础课教学部，山西 阳泉 045000；2.山西大学 物理电子工程学院，山西 太原 030006)

腔量子电动力学(Cavity Quantum Electrodynamics,Cavity QED)由于其优秀的原子与光子之间相互作用的可操控性，已经成为一个研究量子信息处理(Quantum Information Processing,QIP)的范式[1-5].然而，对于一个原子囚禁于量子化光场的系统，高Q值以及将原子精确囚禁于腔内仍然是富有挑战的.在实际量子系统中，量子系统与环境不可避免的相互作用会破坏其相干性.因此，人们提出了各种各样的方案来对抗环境噪声，例如拓扑量子计算[6]、自避错量子计算[7-8]、无消相干子空间[9-26]等等.其中，当环境噪声具有某种对称性时，将量子比特编码在无消相干子空间会是一种简便的方法.例如，为了避免集体消相位错误，可以利用2 个量子比特编码为1 个逻辑比特，即对于集体消相位错误，人们已经提出了一些量子逻辑门和量子通信方案[14-19].例如，魏海瑞等[17]提出了无消相干的量子态转移和量子隐形传态方案.2010 年，陈琼等[16]提出了一个基于低品质腔的无消相干纠缠制备方案，基于低Q腔的量子逻辑门[18]和纠缠浓缩方案也已经提出[19].此外，基于光学系统，夏岩等[20-21]还提出了无消相干的光子极化纠缠态制备方案.最近，利用交叉克尔非线性，在集体旋转无效消相干子空间内的纠缠浓缩方案也被提出来了[22].

不仅如此，在另外一些情况下，当环境噪声是σx型集体噪声时，1 个量子比特会发生如下变化：|0〉→|1〉，|1〉→|0〉.在这种对称性的集体弛豫噪声下，可以将逻辑量子比特编码为算符的2 个本征态此时，1个量子态会演化为所以，量子态 |ψ〉对于集体弛豫错误是免疫的.也就是说，对于1 个量子比特系统，由展开的2 维子空间是一个集体弛豫无消相干子空间(Collective-relaxation Decoherence-free Subspaces，CRDFS).目前为止，只有几个基于超导量子比特系统[23-24]和腔QED 系统[25]的针对集体弛豫的量子计算方案.例如，2018 年，崔文学等[25]提出了对 σx型集体噪声免疫的量子逻辑门和纠缠浓缩方案，但是该方案需要强耦合和高品质腔条件.受之前工作的启发，本文首先提出了2 个构建光子和CRDFS 内逻辑量子比特之间的杂化受控相位翻转(Controlled-phase-flip，CPF)门方案，然后展示了在CRDFS 内的逻辑量子比特之间的纠缠制备方案.在我们的方案中，输入输出过程中由于法拉第旋转效应(Faraday Effect)，光子会根据囚禁腔内原子的不同状态得到不同的反射系数，我们分析了系统参数对反射特性的影响.我们的方案具有以下几个优点：首先，将逻辑量子比特编码在CRDFS 内，使得方案对于集体弛豫噪声免疫.其次，这些方案只需要中度耦合和低Q腔条件，这使得相较于以前的需要强耦合和高Q腔条件的方案，我们的方案实验难度更小.

1 原子-腔系统的输入输出过程

如图1 所示，考虑N个原子囚禁在一个单边光学腔内，每一个原子都具有λ型能级结构，这里PBS 代表一个极化光分束器，C 代表一个光学循环装置.对于第j个原子，|0〉↔|e〉之间的跃迁由H-极化光子驱动，且共振地耦合于腔模，耦合常数为gj.这样的系统具有与Jaynes-Cummings 系统相似的特性，它的哈密顿量为

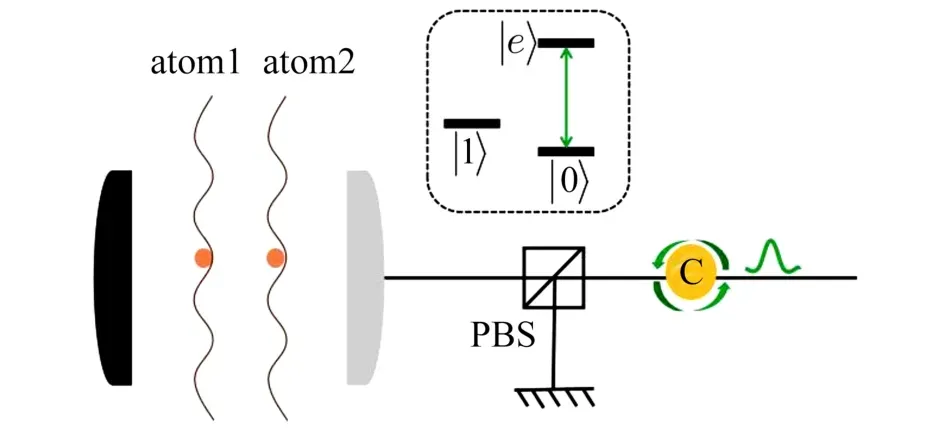
图1 腔辅助单光子输入输出过程示意图Fig.1 Schematic diagram of the cavity-assisted singlephoton input-output process

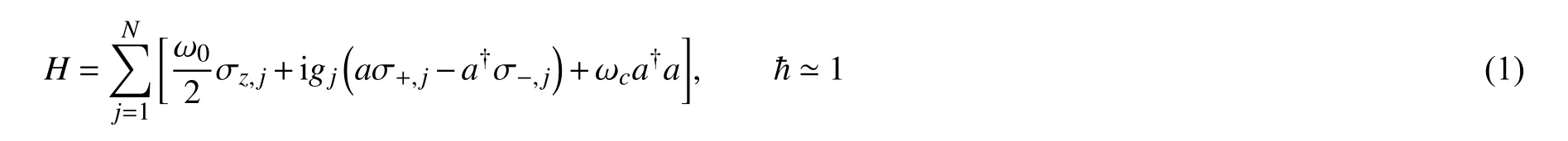
这里 ω0和 ωc分别是原子的跃迁频率和腔场频率，a†和a分别是腔场的产生和湮灭算符，σ+、σ-和σz分别用于表示原子内相应2 个能级之间的的上升、下降和反转算符.

当考虑环境温度很低，可以忽略真空输入场.根据输入输出关系[14,16,27]，得到

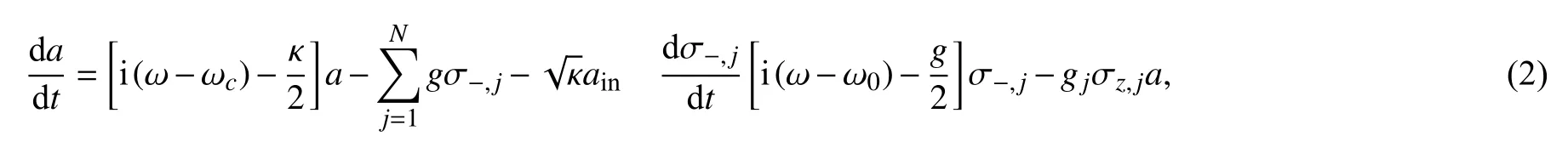
在输入场很弱的情况下，也就是，取〈σz〉≈-1，这个系统的反射系数可以表述为

当输入光子不耦合于腔模时，即g=0 时，得到对于一个冷腔的反射系数

(4)式和(5)式中的反射系数意味着反射光子会根据腔内原子的不同状态经历不同的反射相移.根据以上的讨论，当1 个光子被微腔反射，它会变为1 个输出脉冲，这里rn(ω)是由(4)式和(5)式确定的反射系数.而在本文中，如图1 所示，当2 个原子囚禁于1 个腔内时，对于1 个光子的H-极化部分，当2 个原子都处于 |1〉态，反射系数为r0；当2 个原子都处于 |0〉态，系统的反射系数为r2；而如果仅有1 个原子处于 |0〉态，系统的反射系数将是r1.另一方面，如果输入1 个光子的V-极化部分，它会被PBS 反射而不进入此腔内，此时无论腔内原子处于什么状态，反射光子不会有任何相移，即反射系数为1.

2 基于输入输出过程的杂化CPF 门

为了执行在CRDFS 内的量子信息处理任务，接下来我们说明如何实现1 个光子-逻辑量子比特之间的杂化CPF 门，其可以利用上述的光学旋转选择规则来实现.当腔内仅有1 个原子时，考虑低Q情况，g=κ/2，κ≫γ，当ωc=ω0=ω+κ/2时，根据(4)式和(5)式，可以得到r1=-1，这个过程中的单光子输入输出操作可表达为UR1=exp(-|1〉〈1|⊗|H〉〈H|).在同样的条件下，当腔内囚禁2 个原子时，可以得到r0=i，r1=-1，r2=-i，此输入输出操作可表示为UR2=exp[(-i|00〉〈00|+i|11〉〈11|-|01〉〈01|-|10〉〈10|)⊗|H〉〈H|].

基于上述输入输出过程，可以构建光子和逻辑量子比特之间的CPF 门.为此，将腔内2 个原子编码为这里 |0〉和|1〉是图1 虚线框内所示原子能级.假设输入光子和腔内的逻辑量子比特组成的复合系统初始态为

方法1：第1 个实现杂化CPF 门的方法是基于UR1操作的.过程如下：首先，将原子1 送入腔中而保持原子2 在腔外，让输入光脉冲的H 部分注入腔中.在光脉冲从腔反射出来后就对原子1 执行UR1操作，此操作可记为.其次，将原子2 送入腔中而保持原子1 在腔外，并且通过利用一个光学旋转装置让输入光脉冲的H部分再次注入腔内.在这个相互作用过程之后，就执行1 次操作.实验上已经实现了基于腔QED 系统对原子的囚禁和运输[28-30].最后，需要将原子1 再次移入腔内.这样，杂化CPF 门构建如下：

方法2：为了构建杂化CPF 门，也可以基于UR2操作，按顺序对初始态执行UR2操作，也就是这里代表腔内原子1 对原子2 的受控相位翻转门，它可以以很高的保真度和成功概率实现[29-31].具体过程为：2 个原子始终保持在腔内，首先执行原子1 对原子2 的CPF 操作，其次输入1 个初始态为的光脉冲，在这个相互作用过程之后，执行1 次UR2操作.之后，再次执行原子1 对原子2 的CPF 操作，并且利用一个光学旋转装置让输入光脉冲再次注入腔内，最终执行UR2操作.这个操作过程可以表述为

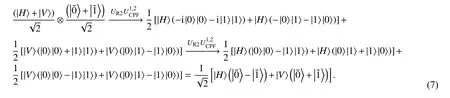
3 在无弛豫子空间内的纠缠态制备

在这一部分，我们说明利用上述的杂化CPF 门实现无弛豫纠缠态的制备方案.如图2 所示装置可以制备2 个逻辑量子比特之间的纠缠态，其中 HWP 代表半波片，D 代表单光子探测器.假设这2 个逻辑量子比特初始制备于态，这里 α，β，γ，δ是归一化常数.令1 个处于态的光子，连续进入2 个腔.HWP 是1 个半波片，其功能是这个混合系统的演化可以具体地写为：

图2 贝尔态制备装置示意图Fig.2 Schematic illustration of setups for Bell states

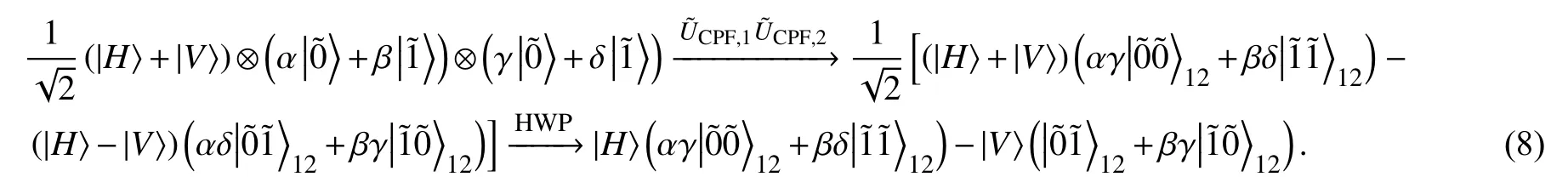
很明显，利用更多的逻辑量子比特，结合自发拉曼绝热通道[32-33]对逻辑量子比特进行合适的单量子比特操作[25]，这个方案可以很直接地拓展来制备在CRDFS 内的多逻辑量子比特Greenberger-Horne-Zeilinger (GHZ)态和团簇态[34].

4 分析与讨论

有必要在实际环境下证明这个模型的可行性并评估我们方案的表现.之前已经有很多方案研究了2个原子囚禁于1 个光学腔内系统的输入输出过程.(3)式的一个关键条件是〈σz〉≈-1，如果保持 κ足够大的话，这一条件总是能满足的，所以(3)式即使在g大于 κ时也是适用的.正如文献[35]所讨论的，在输入输出过程中的弱激发条件也可以通过利用高品质单光子源来满足.我们画出了反射系数的实部(图3(a))和虚部(图3(b))与比率(ωc-ω)/κ之间的关系，这里红色实线代表光子脉冲与原子不耦合的情况(g=0).绿色点划线和蓝色虚线分代表有1 个原子和2 个原子在腔内时的反射系数r1(ω)和r2(ω)，其中采用κ/γ=100.图3 说明，在中度耦合条件下(g=κ/2)，当ωc=ω0=ω+κ/2满足时，我们可以得到想要的反射系数.同时，我们画出了反射系数的实部(图4(a))和虚部(图4(b))与比率g/κ之间的关系，这里红色实线代表光子脉冲与原子不耦合的情况(g=0)，绿色点划线和蓝色虚线分别代表有1 个原子和2 个原子在腔内时的反射系数r1(ω)和r2(ω)，其中κ/γ=100.注意到当g/κ增大时，r0(ω) 趋近于i，这个结果可以写为UR=exp(i|11〉〈11|⊗|H〉〈H|)，这实质上是一个iPHASE 门.此外，我们画出了UR2操作的保真度与比率 γ/κ和g/κ之间的关系，如图5 所示.从图5 可以看出，随着比率γ/κ的增大，UR2操作的保真度逐渐降低，当γ/κ ＜0.01，g=κ/2时，保真度F＞0.971.

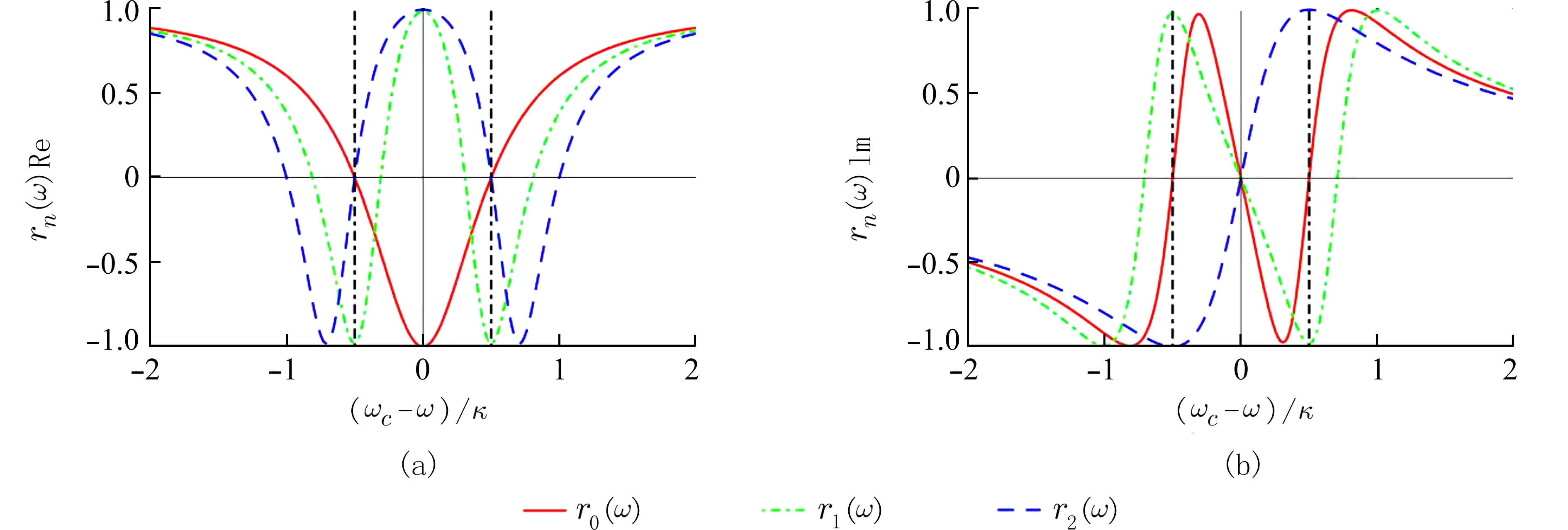
图3 当g=κ/2时，反射系数的实部(a)和虚部(b)与单光子脉冲频率与腔模频率之间失谐量的关系Fig.3 The real part (a) and the imaginary part (b) of the reflection coefficients as functions of the detuning between the input single photon pulse and the cavity mode on condition that g=κ/2

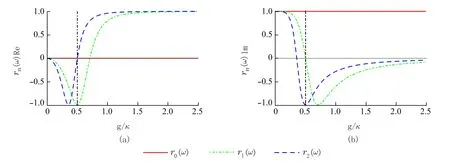
图4 当ωc=ω0=ω+κ/2时，反射系数的实部(a)和虚部(b)与比率g/κ之间的关系Fig.4 The real part (a) and the imaginary part (b) of the reflection coefficients as functio ns of the ratiog/κon condi tion that ωc=ω0=ω+κ/2

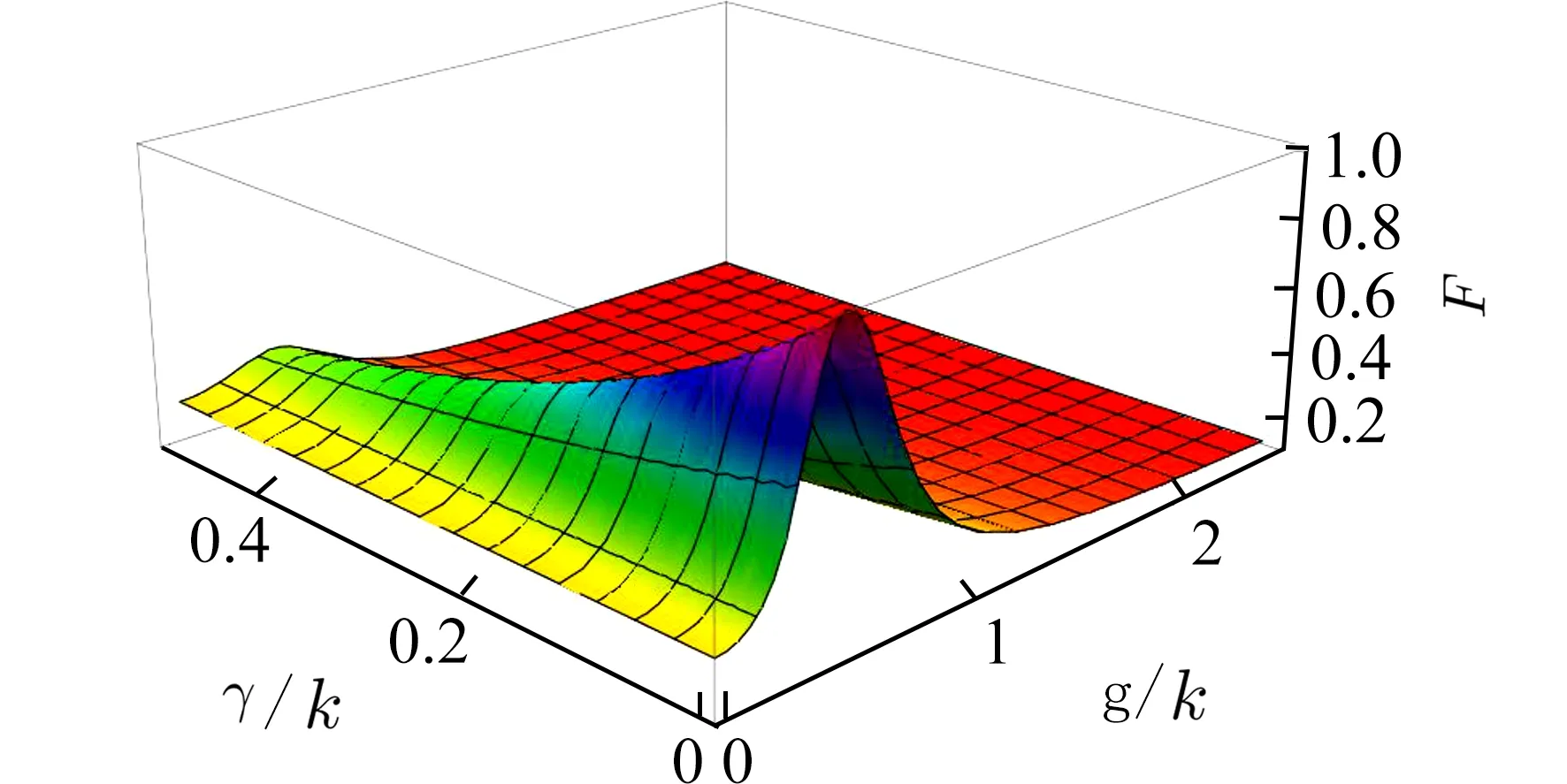
图5 UR2操作的保真度与比率γ/κ和g/κ之间的关系（ωc=ω0=ω+κ/2）Fig.5 The fidelity of theUR2 operation versus the ratioγ/κ and g/κ (ωc=ω0=ω+κ/2 is adopted)

我们的方案要求2 个原子与腔模的耦合常数相等，这从实验角度是有困难的.假设g2=(1+ε)g1，g1=g，我们画出了UR2操作的保真度与 ε之间的关系，如图6 所示.从图6 可以看出，即使存在偏差ε，UR2操作的保真度仍然很高并且随着 |ε|的增大而有轻微下降.例如，ε从-0.2 变化到0.2，UR2操作的保真度仍然大于0.979.所以即使2 个原子的耦合强度存在偏差，这对我们的方案的保真度影响也很小.尽管实验上已经实现了在强耦合条件下中对超冷原子的单独寻址和探测[28]，但是为了能够更好地完成当前方案，仍然需要更好的实验技术.在纠缠制备过程中，原子态的弛豫时间必须比光子间隔时间和操作时间更长，以完成编码和解码量子比特，否则会很难获得高保真度的纠缠态.

图6 UR2操作的保真度与 g2和g1之间偏差 ε关系（假设g2=(1+ε)g1，g1=g.这里ωc=ω0=ω+κ/2）Fig.6 The fidelity of theUR2 operation versus deviationε betweeng2 andg1(Assumeg2=(1+ε)g1,g1=g.Here ωc=ω0=ω+κ/2 is adopted)

在实际情况中，可以考虑2 个87Rb 原子囚禁于1个法布里-珀罗(Fabry-Perot)腔[36].取原子的5S1/2能级的|F=2，mF=±1〉态为基态 |0〉和|1〉，而采用5P3/2的|F′=3，mF=0〉态为激发态 |e〉.此时，跃迁频率为ω0=2πc/λ(λ=780 nm).正如文献[36]报道的，一个F-P 腔的Q值可以达到3.63×106，此时，相关实验参数为[g,κ,γ]/2π=[215,53,3]MHz，如果增大腔镜的透射率，坏腔条件g=κ/2是可以满足的，此时腔的Q值减小到仅仅～105.为了得到(6)式的反射系数，光子脉冲带宽 Δω要远远小于腔模损耗κ，可以精确设定频率失谐量(ωc-ω)，这样可以得到确定的反射系数.这就要求|∂φ/∂ω|ωceΔω ≪π/2(ωce是光子脉冲的中心频率)[22].当Δω ≪κ/2时，这一条件可以很好地满足.实验中可以通过量子点单光子源[33-34]或者纳秒级光脉冲来得到这样的单光子脉冲.

应该强调的是，我们的方案中单光子探测并不会破坏原子的状态，所以方案是以一种“重复直到成功”的方式运行，所以如腔镜吸收、光纤吸收以及探测失效等实验缺陷的存在只会降低方案的成功概率而不会降低方案的保真度.随着逻辑量子比特数的增加，方案的效率会降低，但是原则上它仍然是可拓展的.当利用高品质单光子源(每30 s 产生300 000 个高品质单光子)[35]，本文的方案可以快速完成.

5 结论

基于2 个原子囚禁于单模光学腔系统，分析了其输入输出过程.基于该系统，利用2 个原子编码为1个逻辑量子比特，提出了2 种光子-逻辑量子比特之间杂化CPF 门的方案以及无弛豫的Bell 态制备方案.将量子信息编码在CRDFS，使得我们制备的纠缠态对于集体弛豫错误是免疫的.提出的方案只需要低Q腔条件和原子与腔场之间的中度耦合，这可以降低实验难度.实验缺陷仅仅会降低方案的成功概率而不会降低其保真度.分析结果表明，提出的方案在当前实验条件下可能实现，随着腔QED 系统构造技术的进步，这些方案对未来的量子信息处理会是有用的.