基于决策树的客户流失预测模型
张静怡,胡俊英,李卫斌
(1.厦门大学经济管理学院,福建 厦门 361005;2.西北大学数学学院,陕西 西安 710127;3.西安电子科技大学北斗时空智能研究中心,陕西 西安 710126)
1 引言
随着社会经济的飞速发展,吸引了越来越多的社会资金进入证券市场,然而,由于证券企业管理能力的差异,又导致了证券交易客户的频繁流动.对一个证券企业而言,客户的流失与企业的利润息息相关,有研究表明,对于电信业,银行业等,客户流失率下降5%,就可以为该行业带来25%-85%的利润[1-4].由此可以看出,设计准确的潜在流失客户的预测方法,对这些潜在流失的客户提前采取有效的有针对性的挽留方法,对降低客户流失率至关重要.
近年来,国内外学者对此也进行了很多研究,针对不同行业客户数据的流失预测模型逐渐出现.文献[5-9]利用单调分类法,支持向量机和卷积神经网络网络等方法分别研究了电信用户,网络用户和银行用户的流失影响因素,进而给出了流失预警.文献[10]利用K-means聚类和Logistic回归分析了各种因素对客户流失的影响程度.文献[11]利用随机森林法对数据类噪声滤波基础上提高了分类器的性能,进而对公司客户流失进行预警.文献[12]使用神经网络的自适应算法,将代表离网用户行为特征的45个指标进行样本训练,最终得客户流失行为倾向的判断模型.文献[13]在对XgBoost算法进行改进的基础上建立数学模型预测了电信用户的流失问题.
上述研究主要通过算法的改进,提高模型预测的准确性,几乎所有的方法都是直接对原始数据进行分析处理,缺乏对数据本身蕴含信息的提取和利用,而且所建立的数学模型也是针对具体行业客户数据,导致模型难以推广应用.本文主要通过挖掘证券客户交易数据的深层信息,并利用CART算法[14-15]构建预测模型,以提高潜在流失客户的预测精度.具体地,首先定义合适的时间窗,基于交易数据序列建立信息熵,趋势值和波动值等特征指标体系,再利用CART算法构建决策树模型,用于预测潜在流失客户.在真实数据集上进行实验验证,结果表明本文提出的方法可以准确预测潜在流失客户.
2 相关算法
2.1 CART算法概述
决策树是一种经典有效的回归与分类方法,其中CART算法[8]是应用最广泛的一种决策树学习方法,本文使用决策树中的CART算法来训练一棵二叉树作为预测模型.CART算法由特征选择、树的生成及剪枝三部分共同构成,该算法首先假设决策树是二叉树,递归地二分每一个特征,将特征空间分割成有限个单元,并在这些单元上确定所要预测的概率分布.本文将遵循基尼指数最小化准则,进行特征选取,生成最优决策树.
2.2 基尼指数
分类问题中,假设有K类,样本点所在区域属于第k类的概率值为pk,则概率分布的基尼指数可以被定义为
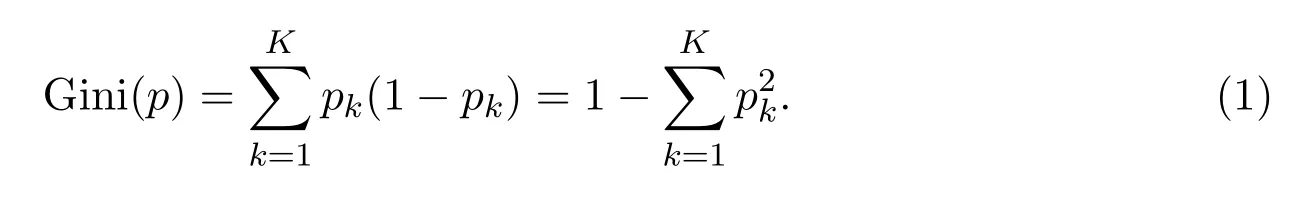
对于二分类问题,若样本点所在区域属于第1类的概率值是p,则概率分布的基尼指数为

对于给定的样本集合D,其基尼指数为
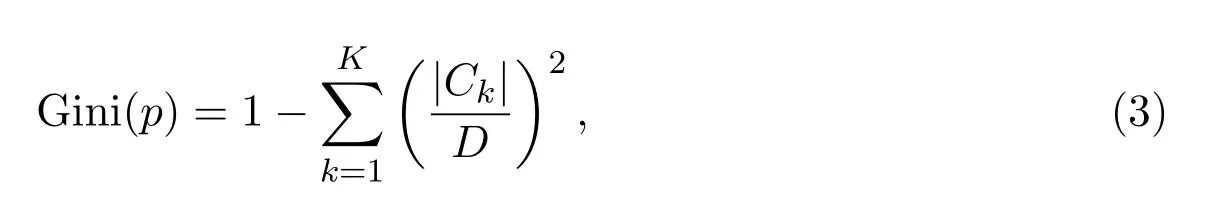
其中,Ck表示D中属于第k类的样本子集,K表示类的总个数.
如果根据特征A是否等于某一可能值a,将样本集合D分割成D1和D2两部分,即D1={(x,y)∈D|A(x)=a},D2=D-D1,则在特征A的条件下,按照下式定义集合D的基尼指数
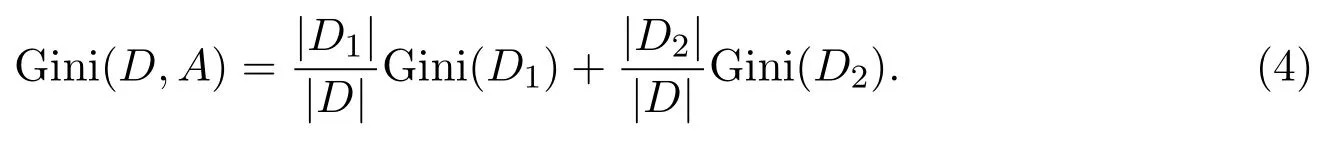
基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性.基尼指数越大,样本集合的不确定性也就越大.
2.3 生成算法
输入:训练数据集D,停止计算的条件;
输出:CART决策树.
根据训练数据集,从根结点开始,依次对每一个结点进行以下处理去构建二叉决策树:
(1)设结点的训练数据集为D,计算已有特征关于该数据集的Gini指数.在这种情形下,对每一特征A,对其可能取到的每一个值a,按照样本点是否满足A=a这一试验条件,分割为D1和D2两部分,再利用(4)式计算A=a时的Gini指数Gini(D,a);
(2)在所有可能的特征A以及他们所有可能的切分点a中,选择Gini指数最小的特征和与其相应的切分点作为最优特征与最优切分点.依最优特征与最优切分点,从现结点生成两个子结点,将训练数据集依特征分配到两个子结点中去;
(3)对两个子结点递归地调用(1)式-(2)式,直至满足停止条件(节点中样本个数小于预定阈值,样本集的Gini指数小于阈值,或者没有更多的特征).
(4)生成CART决策树.
2.4 剪枝算法
输入:CART算法生成的决策树T0;
输出:最优决策树Tα.
(1)设k=0,T=T0;
(2)设α=∞;
(3)自下而上地对各内部节点t,计算C(Tt),|Tt|以及
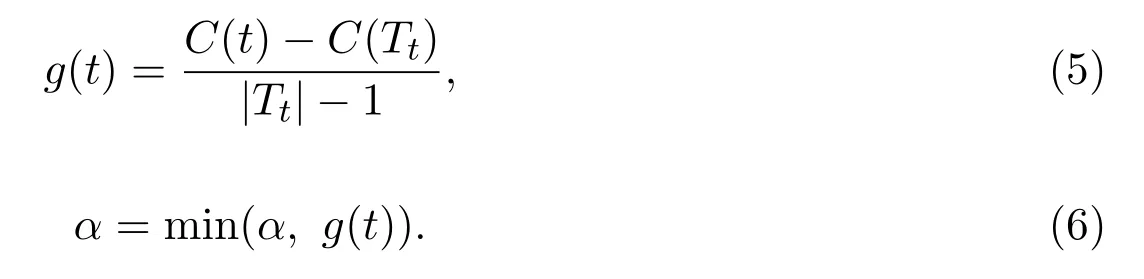
(4)对g(t)=α的内部节点t进行剪枝,并对叶节点t以多数表决法决定其类,得到树T;
(5)设k=k+1,αk=α,Tk=T;
(6)如果Tk不是由根结点及两个叶节点构成的树,则回到步骤(2);否则令Tk=Tn;
(7)采用Cross-validation在子树序列T0,T1,···,Tn中选取最优子树Tα.
3 基于决策树模型的实证分析
3.1 数据获取
本文数据来源于某证券有限公司.数据包含了从2011年7月到2012年10月的16 074个客户交易记录,其中正常客户记录10 000条,销户客户记录6 074条.具体数据由10张信息表组成,包括:
·销户客户和正常客户基本信息表各一张(包括客户ID,开户日期,销户日期,年龄,性别,客户状态,有无客户经理)
·销户客户和正常客户持仓比例表各一张
·销户客户和正常客户交易信息表各一张(包括交易次数,交易额,佣金)
·销户客户和正常客户买入信息表各一张(包括买入次数,买入额,佣金)
·销户客户和正常客户卖出信息表各一张(包括卖出次数,卖出额,佣金)
·销户客户和正常客户日均资产表各一张
·销户客户和正常客户月末资产和证券市值表各一张
·销户客户和正常客户转账信息表各一张(包括转账次数,转账金额)
·销户客户和正常客户转入信息表各一张(包括转入次数,转入金额)
·销户客户和正常客户转出信息表各一张(包括转出次数,转出金额)
3.2 构造数据集
3.2.1 数据预处理
由于原始数据从数据库中导出时会有一些分类错误和数据信息错误的情况,所以需要对原始数据做处理,以便避免错误数据对后续建模的影响.数据预处理包含以下几个步骤:
(1)根据客户状态将销户客户和正常客户正确分类.因为存在从数据库导出数据的过程中,部分销户和正常客户分类错误的现象.
(2)删除错误客户的信息记录.例如:在本数据中,出现了持仓比例大于1的两位客户记录,这显然是错误数据,故将此类客户的所有信息记录剔除.
经过上述两步处理,现有总客户记录16 072条,其中正常客户记录10 355条,销户5 717条.
3.2.2 时间窗口
需要定义预测的输入变量(自变量)和预测变量(因变量)的时间窗口.在自变量时间窗口方面,如果取的时间段太短,不确定因素较多,客户行为有很大的随机性,不具有代表性;取的时间段太长,数据过于陈旧,不能准确反映客户的最新行为趋势.另外,考虑到销户时间在2011年7月到2011年12月底之间的流失客户记录仅为73条,若自变量窗口多属于这6个销户月内,那么在解析问题的时候会由于销户客户的数据量不足,不具有说服力.综上考虑,将自变量窗口时间宽度取为6个月,时间跨度为2012年1月至2012年6月.
对因变量(客户是否流失)的数据窗口来说,为了使得到的预测结果不仅起到预判的作用,又能为营业部提供充足的时间制定策略对客户进行挽留,本文考虑将因变量的时间窗口起点定在自变量时间窗口的一个月之后.定义因变量的时间窗口宽度为3个月.
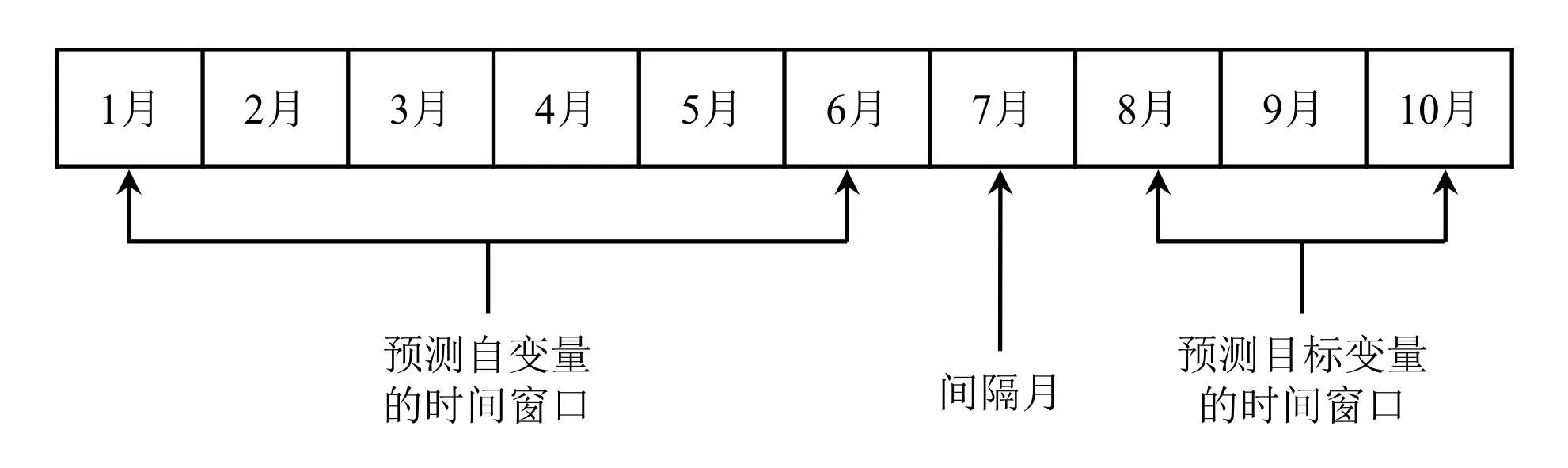
图1 时间窗口表
3.2.3 流失定义
方便起见,本文用0代表正常客户,1代表销户客户.从客户状态来看,这个原始分类仅就销户时间而定.实际上,经分析有些客户虽是未销户的状态0,但表现出的行为特征,比如日均资产减少,交易频率低,账户活跃度低等皆与流失客户的表现一致.虽然从客观上来看,销户日期是鉴定客户是否流失的唯一标准,但若仅仅以销户日期作为客户是否流失的标准必然会对后续模型的建立产生不良影响.鉴于这个考虑,本文结合实际情况,将满足如下两个因素中任意一条即视为销户:
(1)交易记录中有明确的销户日期;
(2)一定时期内无交易记录,且日均资产偏低.
为确定条件(2)中日均资产的临界值,本文利用SPSS对正常客户和销户客户的日均资产从2012年1月到2012年6月的总和做频率分析,结果如表1:
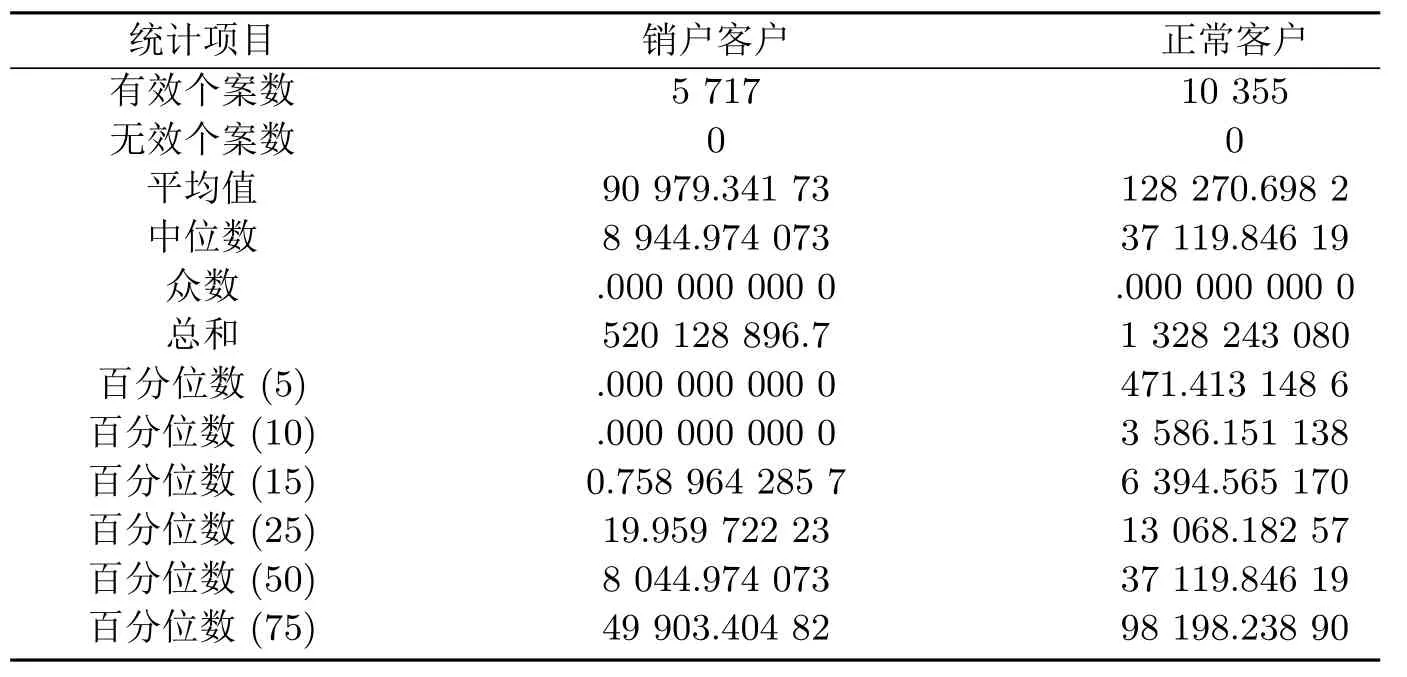
表1 日均资产统计表
由表1可以看出销户客户的日均资产50%的分位点为8 044.974 073,而正常客户日均资产25%分位点就已经是13 068.182 57.为了选取一个日均资产的销户临界值,本文希望尽量地多包含销户客户,而将正常客户的包含率控制在15%以内,同时为了方便筛选数据,对正常客户日均资产15%分位点6 394.565 170向下取整,即得到销户定义所需的日均资产临界值6 395.
在此数据集条件下,第二条销户定义为六个月交易次数和为0且六个月日均资产平均值小于6 395时为流失客户.
此时,在剔除了销户时间在2012年以前的数据记录后,利用EXCEL对原始客户状态进行更改,原来的10 355条正常客户中有1 553条更新为销户状态.并将新的客户状态命名为new client state.
经过客户状态更新,现共有15 999录,其中正常客户记录为9 902条,销户客户记录为7 197条.
3.2.4 指标体系建立
原始交易记录数据虽然能够在一定程度上反映正常客户和销户客户之间的区别,但是具体的区别却很难直接观察得到,因而需要根据实际问题的需要,从实际交易数据中抽取能够反映两类客户真正区别的指标.本文考虑选择客户基本信息,交易次数,交易金额,转账次数,日均资产,持仓比例和证券市值这7个指标作为基础数据,利用这些基础数据构建新的特征指标,具体包括:
(1)趋势类指标
对时间序列而言,趋势变化是一个非常重要的方面.对于证券交易客户,交易次数、持仓比例、日均资产的变化趋势应该能够在一定程度上反映该客户是否可能流失,如果一个客户的交易次数,持仓比例,日均资产的趋势有降低的倾向,那么这个客户流失的可能性将会变大.为能够准确反映某一项统计数据的变化趋势,本文采用以时间为自变量,以一项统计数据为因变量建立回归模型,以回归系数作为该统计数据对应的趋势类衍生指标,具体公式为
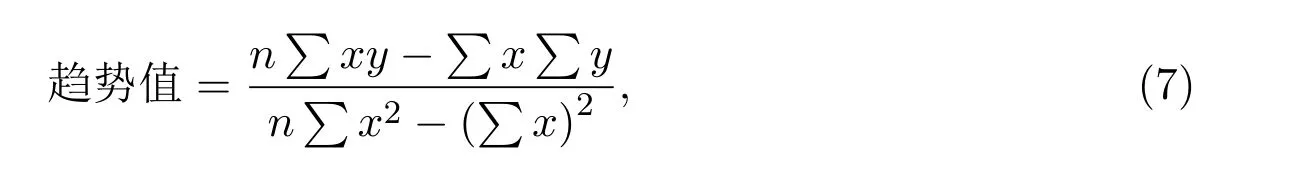
其中,x表示月份,y表示相应指标值,n表示月份数.
(2)波动类指标
趋势可以反映时间序列变化的大致方向,但无法反映变化过程的波动,因此针对统计数据,定义其波动指标为
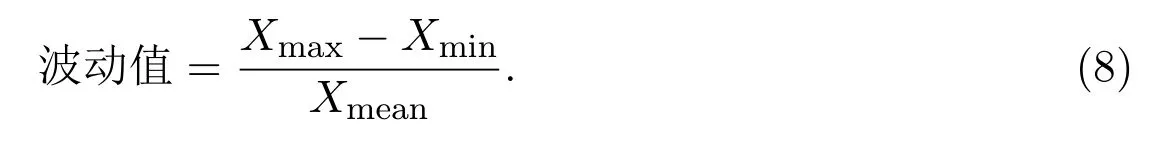
(3)信息熵
将客户的交易数额看作一个随机过程,从而可以用随机变量的信息熵来表示交易过程的不确定性,公式为
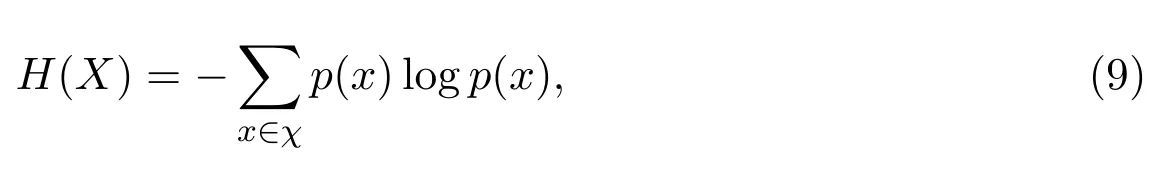
其中p(x)表示统计数据取值为x的概率,具体计算参考集合的特征函数[9]与朴素贝叶斯法参数估计[10]的思想,按照如下方法进行:
Step1:提取每个客户、每个指标在自变量窗口时间下的最大值max;
Step2:将[0,max]等分为五个区间:Ai,i=1,2,···,5;
Step3:按照每个月的指标值xj是否属于区间Ai计算概率
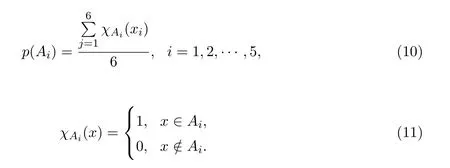
本文按下述步骤进行衍生指标计算,具体结果见表2:
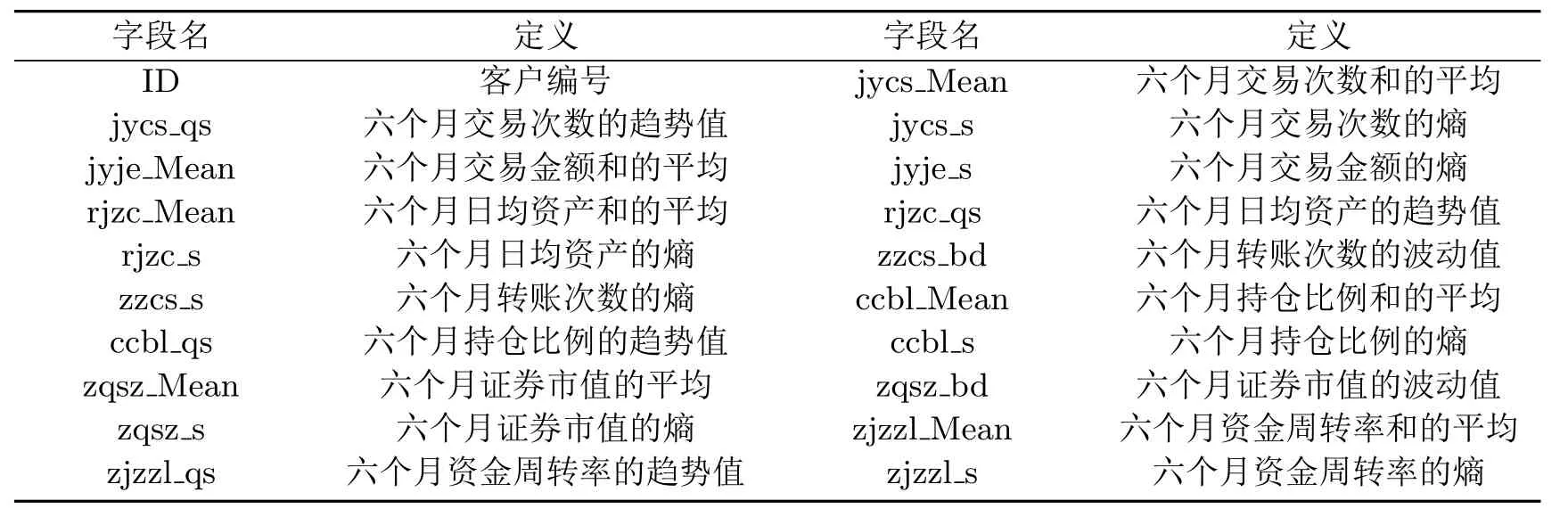
表2 相关字段及定义
(1)将客户六个月的交易次数,交易金额,转账次数,日均资产,持仓比例和证券市值做了汇总平均;
(2)生成交易次数,日均资产,持仓比例的趋势指标;
(3)生成证券市值,转账次数的波动指标;
(4)利用交易金额和日均资产这两个单变量生成资金周转率指标,具体计算公式:资金周转率=交易金额/日均资产,并对资金周转率进行六个月的汇总平均.同时,计算资金周转率的趋势指标;
(5)生成交易次数,交易金额,转账次数,日均资产,持仓比例和证券市值的熵指标;
(6)归一化处理.
为了加快学习算法的收敛速度且使不同量纲的特征处于同一数值的量级,进行min-max归一化,公式如下:

其中,min,max分别为该指标的最小值和最大值.
3.3 数值实验结果
以7:3的比例将原有数据进行随机拆分,分为训练集和测试集两个客户群体.使用CART算法建立决策树模型并在训练集中进行模型训练,基于Gini指数进行分类,在测试集上进行预测,结果在表3中展示,最终构建的部分决策树详情见图2:
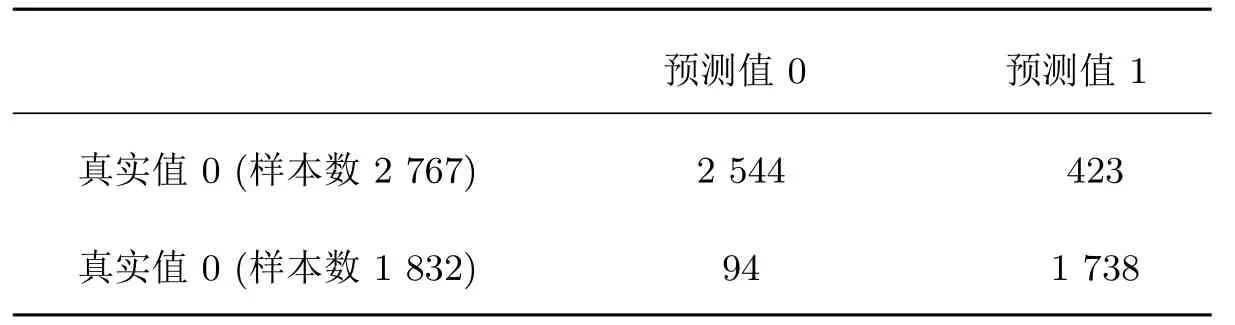
表3 预测结果

图2 部分决策树
可得出建立的预测模型的精确率为89.23%.实验结果表明基于提取的数据的深层特征(信息熵、趋势值和波动值)所构建的预测模型,获得了较高的预测准确度,证明了所用方法的有效性.
4 结论
本文通过提取数据的深层特征,基于这些特征CART算法训练的决策树模型可以较准确地预测到有流失风险的客户,预测成功率达到0.89,模型效果较好,对证券公司客户流失预测的实际应用具有较大的参考价值.通过决策树也可看出,日均资产和持仓比例是衡量顾客是否流失的重要指标,因此,证券公司可据此提供针对性服务,挽留客户.

