Toeplitz算子的频繁超循环性*

郭志涛

(河南工学院 理学部,河南 新乡 453003)

0 引言

其中,N∈N。显然,频繁超循环算子必为超循环算子。

设T表示复平面C上的单位圆周,L2表示T上关于规范化Lebesgue测度平方可积的函数空间,则χn(eiθ)=einθ,n∈Z构成L2上的一组规范正交基。Hardy空间定义如下:

1 幺模特征值准则

Bayart和Grivaux[3]给出了利用特征值判定算子频繁超循环性的“幺模特征值准则”。该准则说明,如果算子T的模为1的特征值所对应的特征向量有足够多,那么T就是频繁超循环算子。以下假设底空间为无限维可分的复Hilbert空间H。

定义1[3]设T为H上的有界线性算子,如果存在T上的一个连续的概率测度σ,使得对任意满足σ(A)=1的σ-可测子集A⊂T,有

则称T具有幺模特征值所对应的特征向量的完美张成集,其中,如果对于每一个λ∈T,都有σ({λ})=0,则称σ为连续的测度。

定理1(幺模特征值准则)[3]设T为H上的有界线性算子,若T具有幺模特征值所对应的特征向量的完美张成集,则T在H上是频繁超循环算子。

2 Tλχ-k的频繁超循环性

利用幺模特征值准则,我们讨论Toeplitz算子Tλχ-k的频繁超循环性。为此,先证明以下引理。

引理1 设λ∈C,k∈N+,则δ是Tλχ-k的特征值等价于|δ|<|λ|。

证明 假设δ是Tλχ-k的特征值,则存在

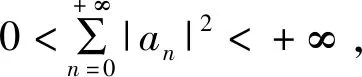
即|δ|<|λ|。

定理2 设λ∈C,k∈N+, |λ|>1,则Tλχ-k是H2上的频繁超循环算子。

证明 由引理1,满足|δ|<|λ|的δ是Tλχ-k的特征值。此时,算子Tλχ-k-δI的核Ker(Tλχ-k-δI)是由以下函数所张成的k-维线性空间:

〈g,f0〉=〈g,f1〉=…=〈g,fk-1〉=0

我们有

…

由于A是T的一个不可数子集,故A在圆盘D(0,|λ|)={z∈C:|z|<|λ|}上有一个聚点;另一方面,函数Φ0,Φ1,…,Φk-1在圆盘D(0,|λ|)上是解析的,因此,我们有Φ0=Φ1=…=Φk-1≡0。由此可知,对于所有的n∈N,有

〈g,χnk〉=〈g,χnk+1〉=…=〈g,χnk+k-1〉=0

从而g=0。所以,Tλχ-k-δI(δ∈A)的核Ker(Tλχ-k-δI)张成H2的稠密子空间。根据幺模特征值准则(定理1),Tλχ-k在H2上是频繁超循环算子。

3 频繁超循环准则

判定算子的频繁超循环性,还有一种证明方法,即下述的“频繁超循环准则”。本文最后,我们利用以下准则给出定理2的另一种证法。

⋮

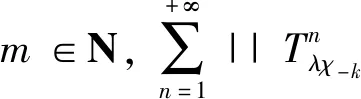
必存在某个正整数t∈N+使得m

另一方面，我们有Snχm=λ-nχm+nk，且

利用频繁超循环准则(定理3)，Tλχ-k是H2上的频繁超循环算子。