浅谈矩阵的初等行变换在线性代数中的应用

张亚龙

(北京科技大学天津学院基础部 301830)

目前，《线性代数》这门课程是理工科和经管类必开设的一门课程，主要内容包括行列式、矩阵、线性方程组、向量组、相似矩阵、二次型等.矩阵的初等行变换贯穿在整个线性代数的内容中，为了方便学生学习，下面归纳总结了关于矩阵初等行变换在线性代数中的应用.

1 矩阵中的应用

1.1 求矩阵的逆

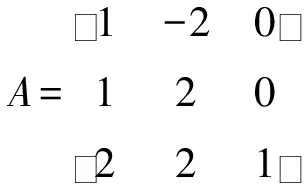
解作一个3×6的矩阵(A，E)，并对其做矩阵的初等行变换.

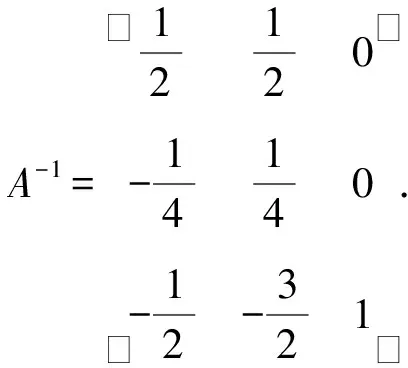
1.2 求矩阵的秩

矩阵秩的定义是非零子式的最高阶数，我们知道初等变换不改变矩阵的秩，对矩阵A做初等行变换化为行阶梯形矩阵B，由行列式的性质可知，矩阵A和矩阵B的非零子式最高阶数相同，所以矩阵A与矩阵B的秩相等.

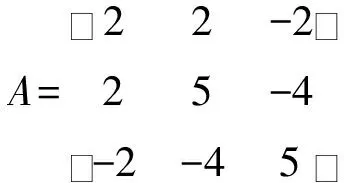
解对矩阵A做初等行变换化为行阶梯形矩阵.

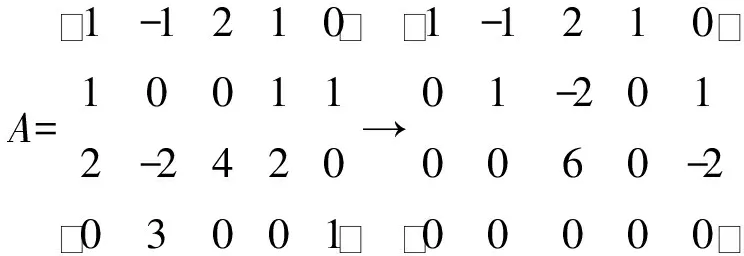
因为矩阵B中有三个非零行，即R(B)=3，所以R(A)=3.

2 在向量组中应用

2.1 求向量组的秩

由于任何矩阵A，它的行秩=列秩=R(A)，因此我们只需将向量组中的向量均按列构成一个矩阵A，向量组的秩就等于矩阵A的秩.

例3求向量组α1=(1，-2，2)，α2=(1，-4，0)，α3=(1，-2，2)的秩.

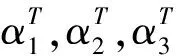
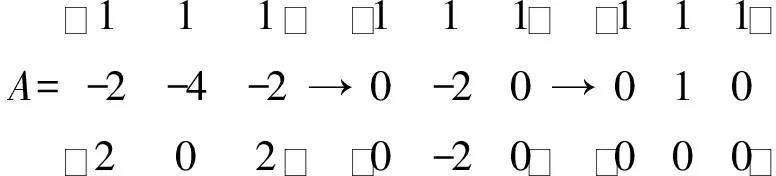
2.2 求向量组的极大无关组

由于初等行变换不改变矩阵列向量的线性关系，因此可由初等行变换求解向量组的极大无关组.

例4求向量组α1=(1,2,3,0)，α2=(-1,-2,0,3)，α3=(2,4,6,0)，α4=(1,-2,-1,0)的一个极大线性无关组.

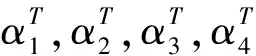
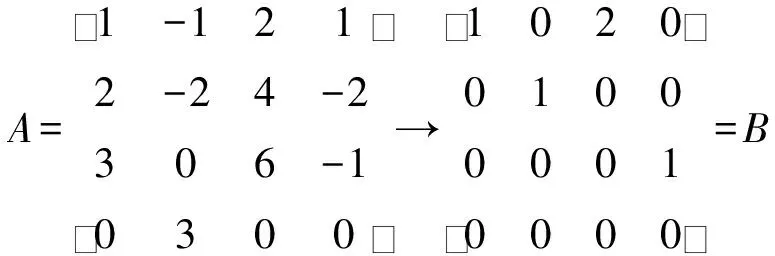
非零行首非零元1所在的列作极大线性无关组，因此向量组α1,α2,α3,α4的一个极大线性无关组为α1,α2,α4.

3 在线性方程组中的应用

通过一系列的初等行变换，将系数矩阵或增广矩阵化为行最简形矩阵，判断方程组是否有解，有解的情况下，求出通解.

3.1 解齐次线性方程组

例5求解齐次线性方程组

3.2 解非齐次线性方程组

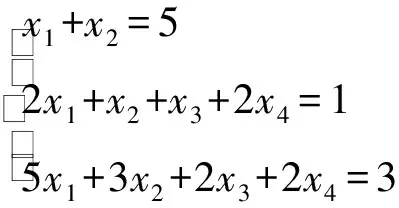
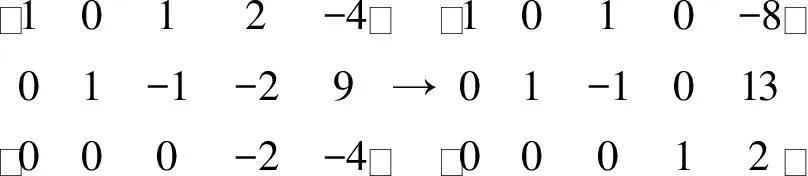
解对增广矩阵B进行初等行变换，化为行最简形矩阵.

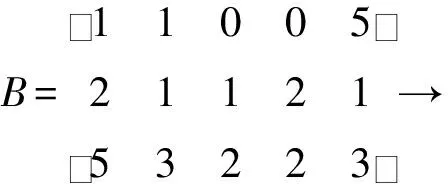
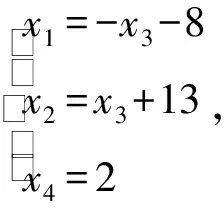
4 在矩阵特征向量中的应用

上面我们介绍了用初等行变换求解线性方程组，计算矩阵的特征向量就会涉及到解齐次线性方程组.

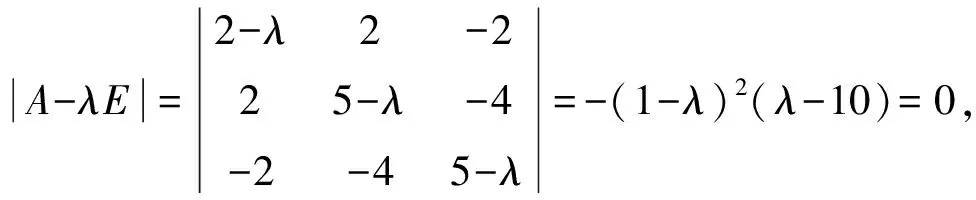
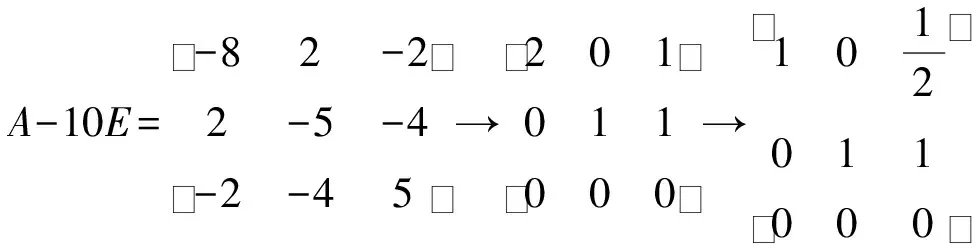
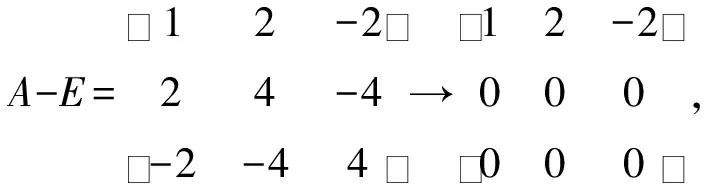
矩阵的初等行变换贯穿于整个线性代数章节中，熟练应用初等行变换是学好线性代数的基础，学生要在平时学习中，学会归纳总结，使每个知识点建立联系.