Design and FPGA implementation of a memristor-based multi-scroll hyperchaotic system

Sheng-Hao Jia(贾生浩)， Yu-Xia Li(李玉霞)， Qing-Yu Shi(石擎宇)， and Xia Huang(黄霞)

College of Electrical Engineering and Automation，Shandong University of Science and Technology，Qingdao 266590，China

Keywords: multi-scroll hyperchaotic attractor，memristor，FPGA

1. Introduction

Since the first chaotic system was found by Lorenz，great interest in chaos phenomena has been shown.[1]At present，the generation of chaotic systems with rich dynamic behaviors has been widely studied.[2–9]As we all know， chaotic systems are extremely sensitive to slight changing of initial conditions. Therefore， chaotic systems have been applied to many engineering fields， such as image encryption，[10–12]secure communication[13，14]and weak signal detection.[15]

In general，the number of scrolls is closely related to the topological complexity of chaotic systems.The phase trajectories of a multi-scroll chaotic system can randomly jump in all scrolls. Thus，comparison with single-scroll and double-scroll chaotic systems，multi-scroll chaotic systems have even more complex dynamic behaviors and topological structures.[16]In recent decades， design and implementation of multi-scroll chaotic systems have been emerging. The multi-scroll chaotic systems can be obtained by introducing a certain kind of nonlinear functions into some existing dynamic systems to expand the saddle-focus equilibrium points(EPs). For example，based on the improved Chua’s system，Liet al. proposed an infinitescroll chaotic system by employing the sine function，and the number of scrolls increases with the increase of the calculating period of the implemented chaotic system.[17]Based on the Jerk system， Wanget al. designed a multi-scroll chaotic system by employing a nested sine-PWL function.[18]On the basis of the Jerk system，Dinget al. presented a grid multi-scroll chaotic system by employing sign function series and a modifying sine nonlinear function， which can generate (m×n)-scroll chaotic attractors.[19]Based on the Chua’s system，Jiaet al. designed a three-dimensional multi-scroll chaotic system by employing logarithmic function series.[20]On the basis of the Sprott-A system，Huet al.realized two simple chaotic systems by employing two different nonlinear functions， which can generate multi-scroll hidden attractors.[21]

In 1971， Chua predicted the memristor as the fourth circuit element， whose constitutive relation is defined on the charge-flux plane.[22]In the last few years， a large number of chaotic systems and hyperchaotic systems are presented by introducing memristors into some existing dynamic systems. Owing to the natural nonlinearity and memory characteristics of memristors， the memristor-based chaotic and hyperchaotic systems possess rich and complex dynamic behaviors such as coexisting attractors[23]and coexisting infinitely many attractors.[24]By means of a smooth flux-controlled memristor， a memristor-based hyperchaotic system is constructed，which has single-scroll，double-scroll and four-scroll hyperchaotic attractors.[25]On the basis of the Jerk system，Liet al. designed a four-dimensional chaotic system by employing a memristor， which can exhibit extremely rich dynamic behaviors.[26]Yanget al. presented a memristor-based four-dimensional hyperchaotic system by introducing a memristor into the Chua’s circuit to replace the resistance.[27]Xuet al. realized an asymmetric memristive diode-bridge(MDB)-based Jerk circuit，which reveals rich and striking dynamic behaviors including periodic limit cycles and chaotic attractors.[28]

In comparison with the multi-scroll chaotic systems and the hyperchaotic systems， the multi-scroll hyperchaotic systems have even more complex and richer dynamic behaviors and better unpredictability. Thus， the multi-scroll hyperchaotic systems are of great research significance. On the basis of the multi-scroll Jerk system， a memristor-based fourdimensional multi-scroll hyperchaotic system is constructed by employing a flux-controlled memristor.[29]Xiaet al. presented two kinds of novel memristor-based multi-scroll hyperchaotic system by adding two new voltage-controlled memristors and a nonlinear function to the Jerk system， which can generate(2N+2)-scroll and(2M+1)-scroll hyperchaotic attractors.[30]By means of the Jerk system， Zhanget al. realized a multi-scroll hyperchaotic system，which can generate(N+M+2)-scroll hyperchaotic hidden attractors.[31]

In addition，the research on the implementation of chaotic systems has also been intensively investigated. At present，there are several methods to implement chaotic systems，which include field programmable gate array (FPGA)，[32–34]analog circuits[35–37]and digital signal processing (DSP).[38，39]The analog circuits have some practical difficulties such as sensitivity of components to the temperature， and the aging of the equipments. As the digital signal processors with highprecision operation， the use of FPGA and DSP digital implementations can effectively avoid these problems. Nowadays，FPGA-based digital implementation of chaotic system is one of the most popular way due to its lower cost and shorter design periods with comparison to the other hardware platforms.

In this paper，a modulating sine nonlinear function and a voltage-controlled memristor are jointly introduced to generate a memristor-based multi-scroll hyperchaotic system. By comparison with many of the existing results， the main innovations of this paper are as follows:

(i) A modulating sine nonlinear function is designed to expand the number of saddle-focus line EPs with index 2. It is convenient to control the number of scrolls by adjusting the parameters of the modulating sine nonlinear function.

(ii)A voltage-controlled memristor is introduced，and by using this memristor， the proposed system can display some complex dynamic behaviors including hyperchaotic attractors and coexisting attractors.

(iii) In contrast with many existing published literature，this paper combines a nonlinear function and a memristor to design a multi-scroll hyperchaotic system.It provides a convenient method to generate multi-scroll hyperchaotic attractors with adjustable scroll numbers.

The rest of the paper is organized as follows.In Section 2，a three-dimensional multi-scroll chaotic system is designed by introducing a modulating sine nonlinear function into a known chaotic system. Then， by introducing a voltage-controlled memristor into the above-designed three-dimensional multiscroll chaotic system， a novel four-dimensional memristorbased multi-scroll hyperchaotic system is proposed and its phase portraits are described. In Section 3， the dynamical characteristics of this system are analyzed by using the stability analysis of EPs， Lyapunov exponents， bifurcation diagrams and basins of attraction. In Section 4， FPGA implementation of the proposed memristor-based multi-scroll hyperchaotic system is designed，and the experimental results of the FPGA-based digital circuit are shown on the oscilloscope.

2. A memristor-based multi-scroll hyperchaotic system

2.1. The design of a modulating sine nonlinear function

In this subsection，a modulating sine nonlinear function is designed to expand the number of saddle-focus EPs with index 2. Thus， the number of scrolls can be expanded conveniently by adjusting the designed modulating sine nonlinear function.

Consider a known chaotic system，[40]the mathematical model of which is

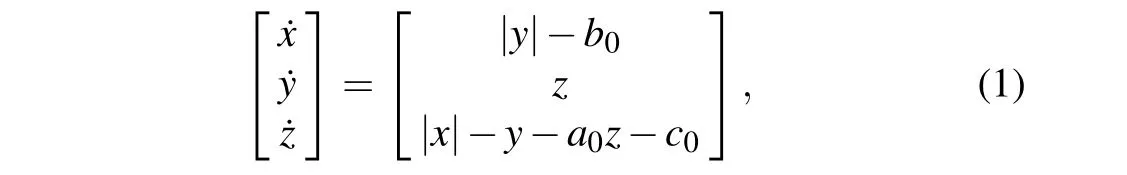
wherex，y，andzare the state variables，anda0，b0，andc0are system parameters.

Based on system (1)， a novel three-dimensional multiscroll chaotic system is proposed as follows:

It should be noticed thatf(y) is a modulating sine nonlinear function， which decides the number of scrolls in system(2). To be specific，since the number of saddle-focus EPs with index 2 is determined by the number of negative slopes of the sine function， we transform the positive slope of the sine function into the negative slope for this purpose. It makes the number of saddle-focus EPs with index 2 doubled. Therefore，the number of scrolls in the proposed system(2)has doubled by employing the modulating sine nonlinear function. When the parametersMandNare set as different values，system(2)can generate multi-scroll chaotic attractors with different number of scrolls. The waveform of the modulating sine nonlinear functionf(y)withM=N=4 is depicted in Fig.1.

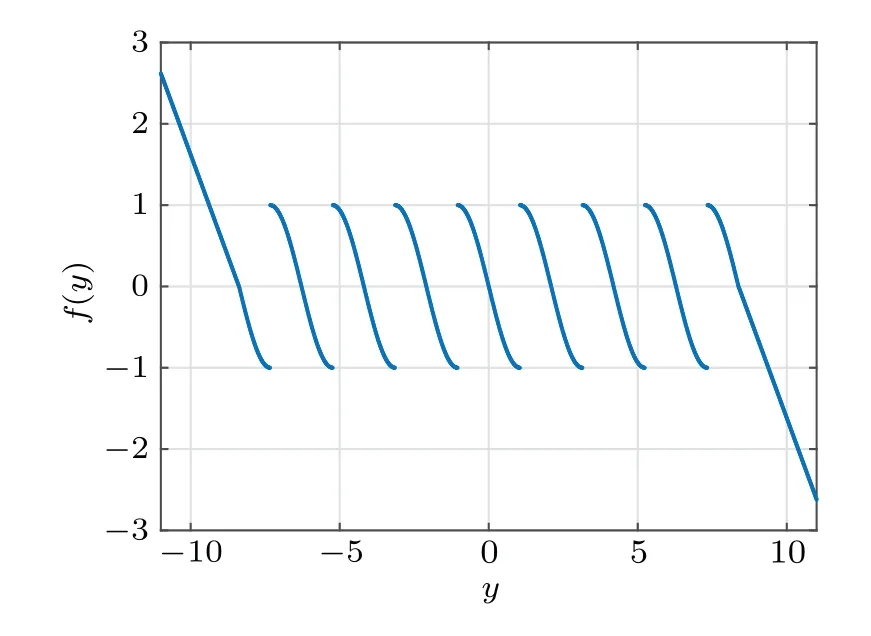
Fig. 1. The waveform of the modulating sine nonlinear function f(y)with M=N=4.

Based on system (1)， the novel multi-scroll chaotic system (2) can be got by expanding the number of saddle-focus EPs with index 2 in theydirection. Taking four groups of parametersM=1，N=2，M=2，N=3，M=N=3 andM=N=4 as examples，the chaotic attractors of the proposed system (2) are displayed in Fig. 2. It can be observed from Fig. 2 that system (2) can generateM+N+1-scroll chaotic attractors，and the number of scrolls is decided byMandN.

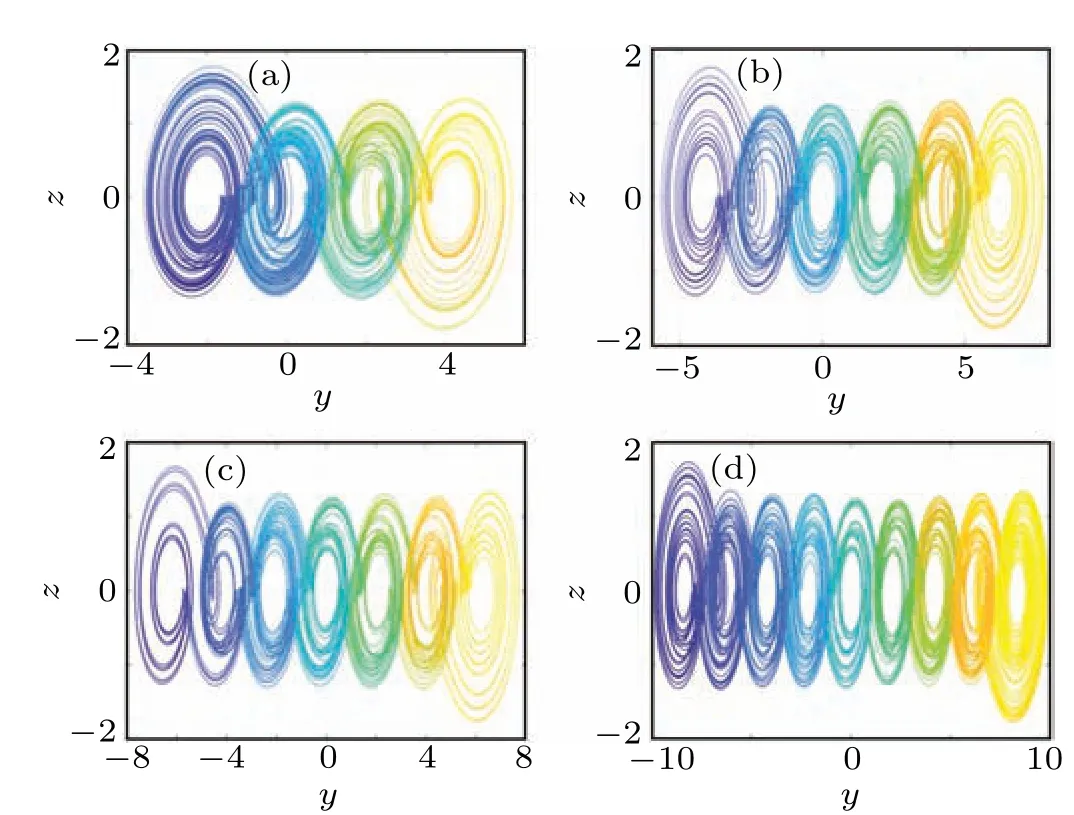
Fig. 2. The chaotic attractors of the system (2) with respect to different parameters M and N: (a) M =1， N =2， (b) M =2， N =3， (c)M=N=3，(d)M=N=4.

2.2. The design of a voltage-controlled memristor

In this subsection， a voltage-controlled memristor is introduced to enrich the dynamic behaviors of system(2). The nonlinear relationship between the voltagevand the currentiof the voltage-controlled memristor can be expressed as

whereW(φ) is the memductance function. In this paper， a quadric nonlinearity function is selected， which is defined asW(φ)=-0.5+φ2.

To get a memristor-based multi-scroll hyperchaotic system，the voltage-controlled memristor defined in Eq.(5)is introduced into system(2). Then，a new memristor-based multiscroll hyperchaotic system is proposed as follows:

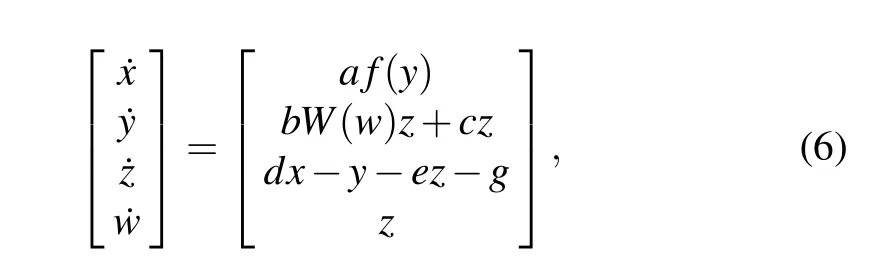
whereW(w)=-0.5+w2andf(y)is the modulating sine nonlinear function defined in Eq.(3).

Next，it will be shown that system(6)can generate hyperchaotic attractors with controllable number of scrolls in theydirection. When the parameters are selected asa=3，b=g=1 andc=d=e=0.5， system (6) can generate multi-scroll hyperchaotic attractors. Meanwhile， the number of scrolls is decided by the parametersMandNof the modulating sine nonlinear functionf(y). It means that system(6)can generateM+N+1-scroll hyperchaotic attractors for different values ofMandN. Taking four groups of parametersM=1，N=2，M=2，N=3，M=N=3 andM=N=4 as examples，and the initial conditions are taken as(0， 0， 0， 0)T，system(6)can generate 4-scroll， 6-scroll， 7-scroll and 9-scroll hyperchaotic attractors， respectively. Correspondingly， the phase portraits of the 4-scroll，6-scroll，7-scroll and 9-scroll hyperchaotic attractors in they-zplane are described in Fig.3.It can be clearly concluded from Figs.2 and 3 that，owing to the introduction of the memristor(5)，the system(6)can generate multi-scroll hyperchaotic attractors with different sizes， in contrast with the multi-scroll chaotic attractors in system(2).

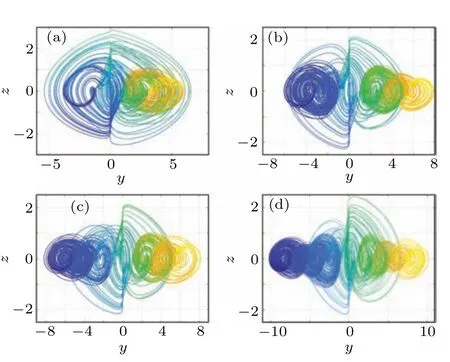
Fig. 3. The hyperchaotic attractors of the system (6) with respect to different parameters M and N: (a)M=1，N=2，(b)M=2，N=3，(c)M=N=3，(d)M=N=4.

3. Dynamic analysis

In this section，the dynamical characteristics of system(6)are further analyzed， such as the EPs and their stability， Lyapunov exponents， bifurcation diagrams and basins of attraction.

3.1. EPs and their stability analysis

By comparison with system(2)，the number and the properties of the EPs of system(6)have changed greatly，because of the introduction of the memristor (5). At a result， the EPs of system(2)have been extended to line EPs. To get the line EPs of system(6)，let ˙x= ˙y=˙z= ˙w=0，then

It can be clearly seen from the above analysis that the number of critical EPs and saddle-focus line EPs with index 2 changes for varying values of the parametersMandN. Therefore，when the parametersMandNare set as different values，the corresponding number of critical EPs and saddle-focus line EPs can be expended. Note that，the saddle-focus line EPs are very important to generate chaotic attractors， and the number of saddle-focus line EPs with index 2 has a one-to-one correspondence with the number of scrolls. Therefore， we can control the number of scrolls of attractors by selecting appropriate parametersMandN，and then theM+N+1-scroll hyperchaotic attractor can be obtained.

3.2. Lyapunov exponents and bifurcation diagrams

To explore the influence of the nonlinear function(3)and the memristor (5) to the nonlinear dynamical characteristics of system (6)， the Lyapunov exponents and bifurcation diagrams with respect to parametersaandbare investigated in this subsection. For simplicity， only system(6)with parametersM=N=4 is used as an example to explore the dynamical characteristics. The MATLAB simulation results are shown in Figs.4 and 5 with initial conditions(0， 0， 0， 0)T.

Fig.4. Lyapunov exponents and bifurcation diagram of the system(6)with respect to a: (a)Lyapunov exponents;(b)bifurcation diagram.

Whenb=g= 1 andc=d=e= 0.5， the Lyapunov exponents and bifurcation diagram are shown in Fig. 4 with respect to the parameteravarying in the range 0＜a ＜5.It can be clearly seen from Fig. 4 that system (6) in turn goes through period， chaos and hyperchaos with the increase of parametera. When 0＜a ＜0.91， the sign of the Lyapunov exponents are (0， 0，-，-)， so the attractors is periodic. When 0.91＜a ＜1.58，the sign of the Lyapunov exponents are (+， 0，-，-)， so the system is in a chaotic state.When 1.58＜a ＜5， the sign of the Lyapunov exponents are(+， +， 0，-)， it implies that the system is in a hyperchaotic state. It can be concluded that the hyperchaotic system(6)has even more complex dynamical characteristics than the chaotic system(2).

On the other hand，when the parameterbvaries from 0 to 9，the Lyapunov exponents and bifurcation diagram are shown in Fig. 5 witha=3，g=1 andc=d=e=0.5. It can be concluded from Fig.5 that system(6)possesses sustained hyperchaotic state with the increase of parameterb， and the bifurcation diagram match well with the Lyapunov exponents.

Fig.5. Lyapunov exponents and bifurcation diagram of the system(6)with respect to b: (a)Lyapunov exponents;(b)bifurcation diagram.

3.3. Coexisting multi-scroll hyperchaotic attractors

To further explore the influence of the memristor(5)upon the dynamic behaviors of system (6)， the coexisting multiscroll hyperchaotic attractors are investigated in this subsection. For simplicity， the system parameters are set asa=3，b=g=1，c=d=e=0.5 andM=N=4 to explore the coexisting hyperchaotic attractors by analyzing the Lyapunov exponents，bifurcation diagrams and basins of attraction.

When the initial conditions of system (6) are set to be(0，y(0)， 0， 0)T， the Lyapunov exponents and bifurcation diagram are described in Fig.6 with respect to the initial conditiony(0) varying in the range-9＜y(0)＜9. It can be seen from Fig.6(a)that system(6)remains sustained hyperchaotic state and the Lyapunov exponents vary for different initial conditionsy(0). It is observed from Fig.6(b)that the bifurcation diagram has a symmetric relationship about the origin. To better show this interesting phenomenon， some phase portraits are given with different initial conditions. The hyperchaotic attractors of system(6)are displayed in Fig.7 with the initial conditions(0，y(0)， 0， 0)T，wherey(0)is set to be±2.3，±4.4 and±6.2. It is observed from Fig.7 that system(6)can produce 9-scroll hyperchaotic attractors. In addition， when two initial conditions are opposite to each other， the hyperchaotic attractors have a symmetrical positional relationship about the origin.

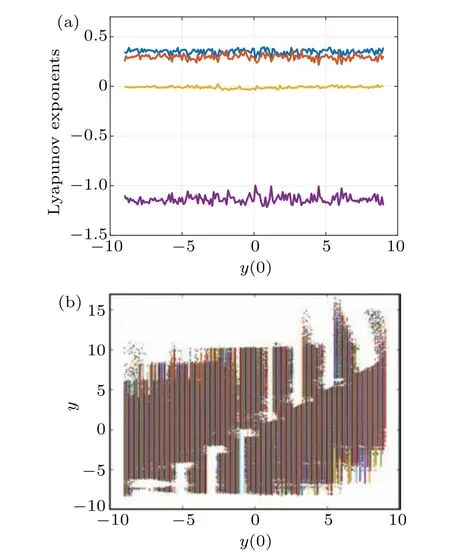
Fig.6. Lyapunov exponent and bifurcation diagrams of the system(6)with respect to the initial conditions (0， y(0)， 0， 0)T: (a) Lyapunov exponents;(b)bifurcation diagram.

When the initial conditions of system (6) are set to(0， 0， 0，w(0))T，the Lyapunov exponents and bifurcation diagram are described in Fig.8 with respect to the initial conditionw(0) varying in the range-9＜w(0)＜9. From Fig. 8，it can be concluded that the Lyapunov exponents and bifurcation diagram are approximately symmetric aboutw(0)=0，and system (6) stays on sustained hyperchaotic state with respect to the initial conditionw(0)in the range-9＜w(0)＜9.For instance，whenw(0)is set to be 1，3.5，5 and 8，the system can generate 9-scroll，4-scroll，double-scroll and single-scroll hyperchaotic attractors， respectively. From Fig. 9， it can be seen that the number of scrolls of system (6) varies with the change of the initial conditionw(0).

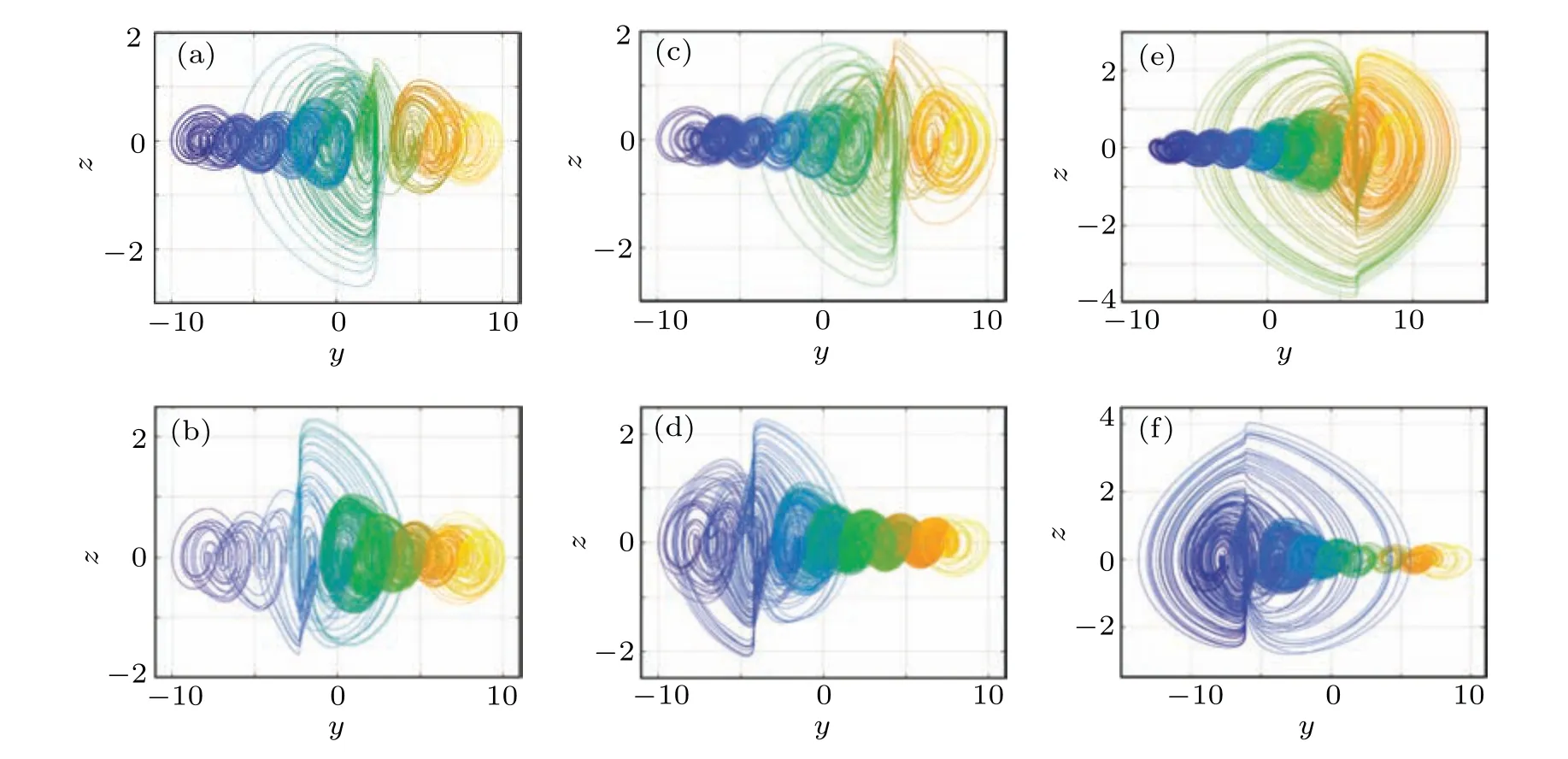
Fig.7. The hyperchaotic attractors of the system(6)with respect to different initial conditions: (a)(0， 2.3， 0， 0)T;(b)(0， -2.3， 0， 0)T;(c)(0， 4.4， 0， 0)T;(d)(0， -4.4， 0， 0)T;(e)(0， 6.2， 0， 0)T;(f)(0， -6.2， 0， 0)T.

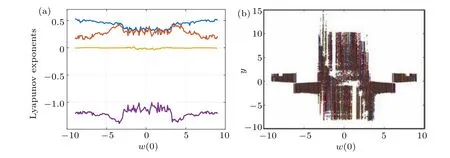
Fig. 8. Lyapunov exponents and bifurcation diagram of system (6) with respect to the initial conditions (0， 0， 0， w(0))T: (a) Lyapunov exponents;(b)bifurcation diagram.

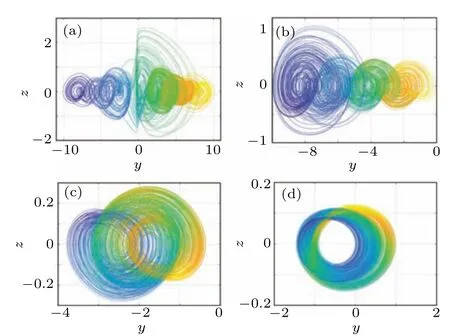
Fig. 9. The hyperchaotic attractors of system (6) with respect to different initial conditions: (a) (0， 0， 0， 1)T; (b) (0， 0， 0， 3.5)T; (c) (0， 0， 0， 5)T;(d)(0， 0， 0， 8)T.

To further confirm that system (6) has coexisting hyperchaotic attractors，the basins of attraction of the system(6)iny(0)–w(0)plane are displayed in Fig.10 with the initial conditionsx(0)=z(0)=0. Different colors in Fig.10 represent different types of hyperchaotic attractors，in which white represents system divergence，yellow represents the single-scroll hyperchaotic attractor，brown represents the double-scroll hyperchaotic attractor，green represents the 4-scroll hyperchaotic attractor and gray represents the 9-scroll hyperchaotic attractor. It is worth noting that， for simplicity and intuition， only five color regions are labelled in the basins of attraction. In fact，for different initial conditions，the various types of attractors can be found in system(6)，such as 9-scroll hyperchaotic attractors with different topological structures.

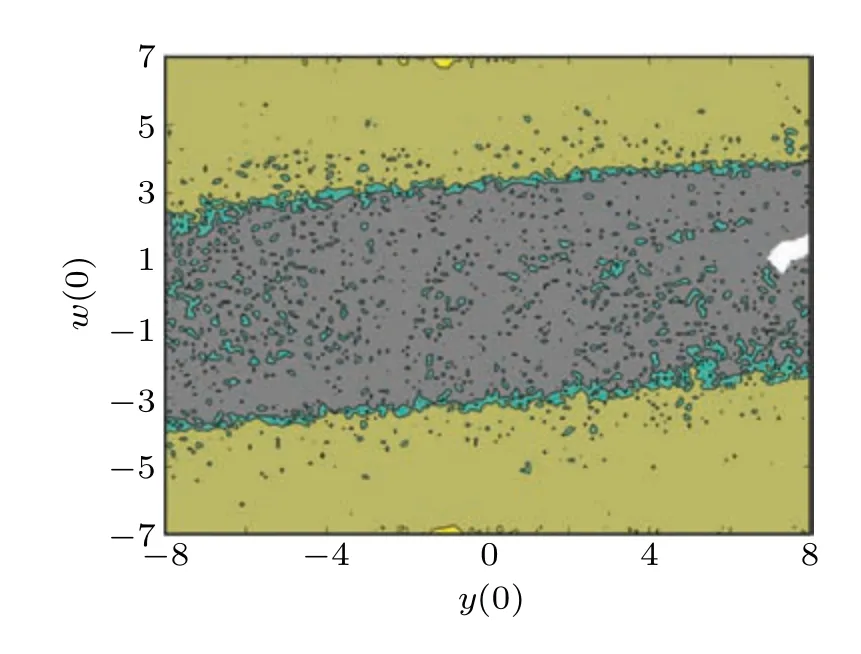
Fig.10. The basins of attraction of the system(6)in y(0)–w(0)plane.

It can be concluded from the above analysis that there exist various coexisting hyperchaotic attractors in system(6)，owing to the introduction of the memristor (5). This phenomenon means that，in contrast with system(2)，the state trajectories of system (6) are even more sensitive to the initial conditions， and it implies that system (6) has even richer dynamic behaviors than many existing memristor-based chaotic systems.

4. FPGA implementation

In this part，the FPGA-based digital implementation is designed for the proposed multi-scroll hyperchaotic system(6).Meanwhile， the hyperchaotic attractors with different initial conditions are implemented by FPGA. Firstiy， the hyperchaotic system is described by the improved Euler algorithm.The discrete state equation of the memristor-based multi-scroll hyperchaotic system(6)is described as follows:

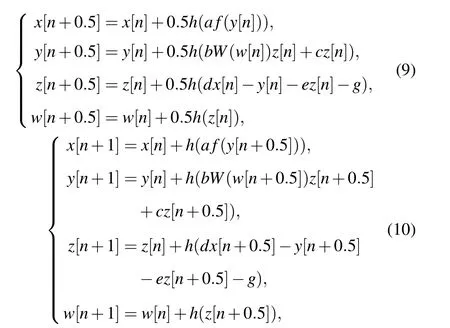
with

In Eqs. (9) and (10)，his the iteration step and set to beh=1/128. Then，the iteration operation of Eqs. (9)and(10)can be described by employing a three-stage state machine.Finally， the output digital signals in the FPGA development board are converted into the analog voltage signals， and the phase portraits of the multi-scroll hyperchaotic attractors of system(6)are displayed on the oscilloscope.

Firstly， for the high operation accuracy requirement， the state variables are described by employing 32-bit fixed-point numbers. In this 32-bit fixed-point numbers， we use 1 bit to represent the sign bit， 7 bits to represent the integer part and 24 bits to represent the decimal part. Then，the digital implementation of system(6)is designed.The iteration operation of Eqs.(9)and(10)can be easily realized by using the three-stage stage machine.The design of the three-stage state machine for the hyperchaotic system(6)is displayed in Fig.11.

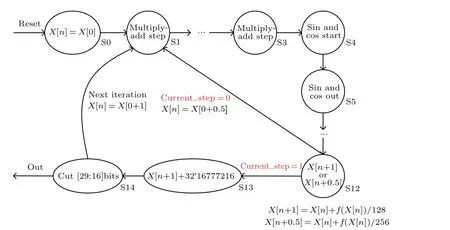
Fig.11. State machine description of the system(6).

Thereafter，Eqs.(9)and(10)are directly described in the Quartus II design software by using the Verilog HDL language.Then，the Verilog HDL code of the FPGA-based digital implementation is downloaded to the FPGA chip after compilation. The FPGA chip is Altera Cyclone IV EP4CE10F17C8 and the DAC module is AN9767. The digital signals can be converted into analog voltage signals to display on the oscilloscope， by employing the DAC module. To prove the feasibility of the design method，the experimental equipment based on FPGA is tested and shown in Fig.12.

Fig. 12. Experimental testing of the memristor-based multi-scroll hyperchaotic system.

Setting all the system parameters asa=3，b=g=1，c=d=e= 0.5 andM=N= 4， we can obtain the hyperchaotic attractors of system (6) corresponding to different initial conditions as shown in Fig.13， respectively. Form Fig.13， it can be clearly seen that the hyperchaotic attractors of system (6) displayed on the oscilloscope are all in accordance with the numerical simulation results of MATLAB in the Figs.3，7 and 9. The existence of the hyperchaotic attractors is confirmed in Fig.13.

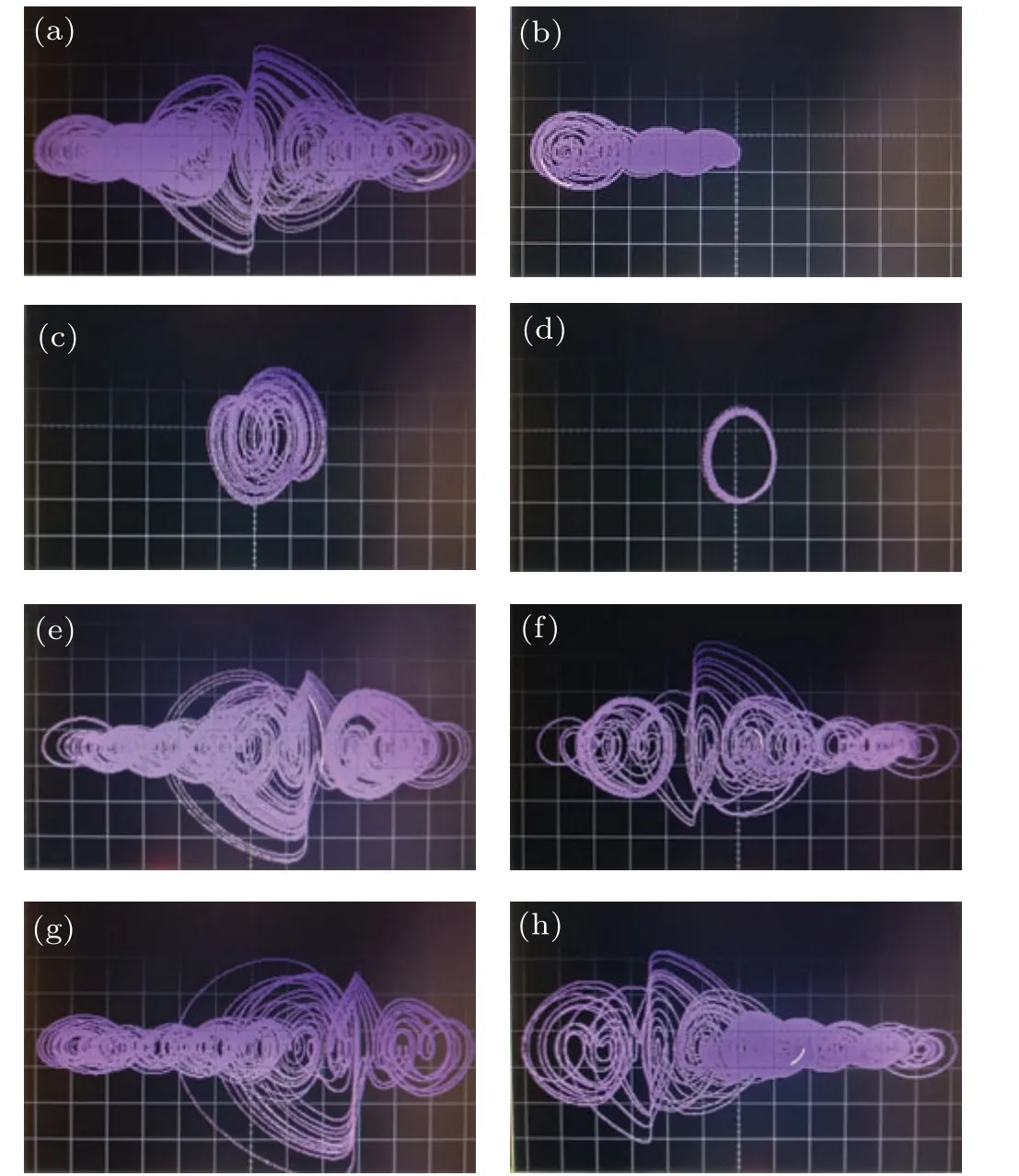
Fig.13. The experimental results with respect to initial conditions: (a)(0， 0， 0， 0)T; (b)(0， 0， 0， 3.5)T; (c)(0， 0， 0， 5)T; (d)(0， 0， 0， 8)T;(e) (0， 2.3， 0， 0)T; (f) (0， -2.3， 0， 0)T; (g) (0， 4.4， 0， 0)T; (h)(0， -4.4， 0， 0)T.

5. Conclusion

The paper proposes a novel method to generate multiscroll hyperchaotic attractors by employing a modulating sine nonlinear function and a voltage-controlled memristor. A novel memristor-based multi-scroll hyperchaotic system is constructed which can produce coexisting hyperchaotic attractors with different topological structures， and meanwhile the multi-scroll hyperchaotic system (6) is realized by FPGA. In contrast with most of the existing results， the main innovations of this paper are as follows: To increase the number of scrolls， the modulating sine nonlinear function (3) is designed to change the number of saddle-focus line EPs with index 2. Thus，the number of scrolls can be controlled by selecting appropriate parametersMandNin the modulating sine nonlinear function(3). On the other side，owing to the introduction of the voltage-controlled memristor(5)，the proposed system (6) can generate various complex dynamic behaviors，such as hyperchaotic attractors and coexisting attractors(e.g.，M+N+1-scroll，4-scroll，double-scroll and single-scroll hyperchaotic attractors)，in comparison with the multi-scroll system(2). Hence，it is more convenient to generate multi-scroll hyperchaotic attractors with controllable scroll numbers than many of the existing published literature. In summary，in contrast with many chaotic systems，the presented multi-scroll hyperchaotic system has larger key space and more complex dynamic behaviors，and therefore is especially suitable for engineering applications.

Acknowledgements

Project supported by the National Natural Sciene Foundation of China(Grant Nos.61973199 and 61973200)and the Taishan Scholar Project of Shandong Province of China.