直驱式输电线路作业车BP神经网络调速控制

马利群，范学军，阚志忠

(1.邯郸欣和电力建设有限公司，河北 邯郸 056004； 2.国网河北省电力有限公司邯郸供电分公司，河北 邯郸 056004； 3. 燕山大学 电气工程学院, 河北 秦皇岛 066004)

0 引言

在电力系统中进行封网施工作业是防止在更换“三跨”型输电线路(跨铁路、跨高速、跨输电通道)导地线过程中，因导地线坠落可能导致严重交通事故的有效手段。利用封网作业车替代传统人力方式可使得施工人员避免身处高危环境，防止人员高空摔落及触电，节省封网作业成本和时间。研究能够适应多种工况(架空线线径，档距、弧垂、导线表面摩擦力等诸多不同)、对线路损伤低、可满足穿越带电线路、高速公路电气化铁路等线路进行封网的直驱式轻型封网作业车具有重要的实用价值[1]。

如图1所示的永磁直流电机直接驱动滚轮在线路上运行的封网作业车因省却减速齿轮，具有结构简单、重量轻等优点，但也因电机轴与被拖动滚轮直接耦合导致其转轴机械转动惯量易受负载惯量变化影响，电机运行在柔性轨道，其转速易受到负载特性变化的直接影响。直驱式封网作业车直流电机调速系统面临高空不确定性风阻力和摩擦阻力等扰动，且直流电机调速系统存在多变量耦合、系统非线性以及系统参数时变、不确定等扰动问题。为改善传统的固定系数比例、积分、微分(PID)控制性能，有学者对自适应、模糊、神经网络PID相融合的智能控制算法开展了研究工作[2-3]，但是此文献中的被控制对象并非为多变量耦合的电机系统，进入21世纪的近十年，研究人员试图进一步将智能算法与PID控制器相结合应用于通用型机电运动系统[4-12]，这样既保留了传统PID控制的特有优势，又能够在线实时调整PID参数，从而保证被控制对象具有良好的动静态性能。人工神经网络为解决非线性、参数不确定系统的控制问题提供了一种方法，其中文献[4-5]将BP神经网络PID控制方法初步应用于直流电机控制，以应对某些控制环境条件变化对传统PID直流电机转速控制性能影响，但此两篇文献均未有针对性地明确提及影响直流电机转速控制性能的具体环境条件。此后，文献[6-10]研究了永磁电机的转速BP神经网络控制方法，永磁电机作为一种多变量、强耦合的非线性系统，要求控制算法实时性高，此文献提出的方法存在算法复杂不容易实现的问题。文献[6]在把无刷电机为单输入单输出特殊非线性模型基础上，开展BP神经网络PID控制研究，文献[7]研究了变更神经网络学习速率的无刷直流电机神经网络控制，文献[8]研究了基于Q学习优化神经网络连接权重的无刷电机控制，文献[9] 研究了无刷直流电机驱动器的模糊神经网络(FNN)学习控制方法。FNN将模糊逻辑与人工神经网络的学习能力相结合。设计了一个FNN结构，并定义了四种不同的FNN训练算法，文献[11]研究了利用神经网络提高风电装配平台中液压伺服系统位置控制精度的方法。文献[12]将BP神经网络应用于磁悬浮轴承磁轴承控制，以改善磁悬浮轴承的动态性能。

本文将BP神经网络算法与传统PID相结合，研究直驱式封网机作业车的转速控制，提高作业车协同工作能力，抗输电线路挠度变化、摩擦力变化、负载质量变化等扰动，提出一种以转速闭环控制响应特性为目标的神经网络连接权重修改方法。通过神经网络学习自动整定PID参数，使得直驱式直流电机调速系统能够适应电机转轴转动惯量宽范围变化对调速系统稳定性的影响，最终使得直流调速系统具有良好的调速性能。

1 直流电机调速系统数学模型

1.1 直流电机动态模型

图2为他励直流电机电枢回路的等效电路和电机轴拖动负载运行的机械系统简化模型，其中Udc为电枢电源电压，L为电枢回路的漏电感，R为电枢回路总电阻，E表示电机电枢电动势(简称电势)，Id为电枢电流，n表示电机轴转速，直流电机的电枢回路动态方程以及电动机轴的动力学方程分别为

图2 直流电机与负载的等效模型Fig.2 Equivalent model of DC motor and load

(1)

(2)

式中:TL为折算到封网直流电机轴的负载转矩，包括摩擦力，风阻力，重力；GD2为电机轴上总飞轮惯量，为电机轴和负载惯量折算到电机轴的转动惯量之和。

在额定励磁作用下，直流电机的感应电动势E和电磁转矩Tem分别为

E=Cen，

(3)

Tem=CmId，

(4)

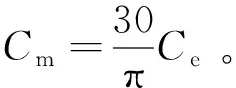
定义直流电机电枢回路的电磁时间常数，Tl和机电时间常数Tm分别为

(5)

(6)

此时将式(5)和式(6)代入式(1)和式(2)，并结合式(3)和式(4)，整理后进行拉氏变换分别得

(7)

(8)

式中，IdL为负载电流。

结合式(7)和式(8)，得到直流电机的动态结构框图，如图3所示。

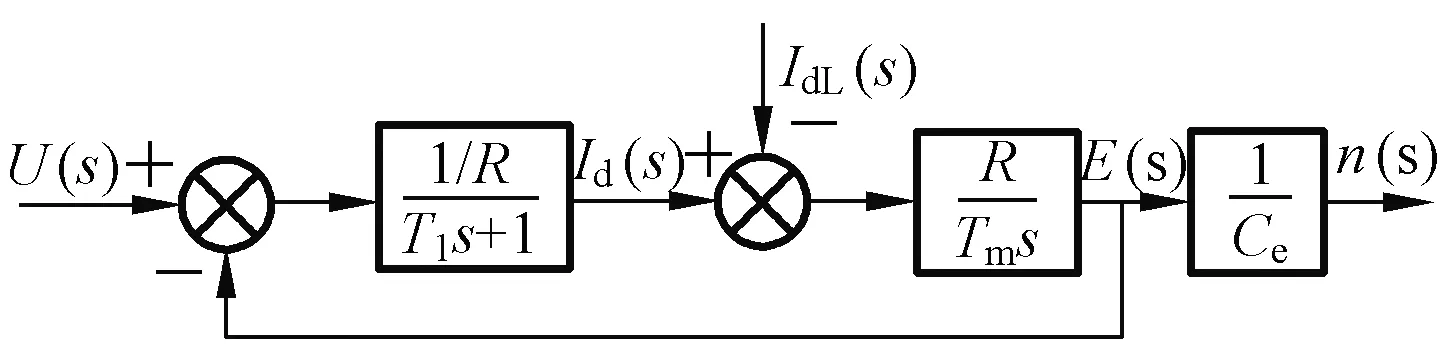
图3 直流电机的动态结构框图Fig.3 Block diagram of dynamic DC motor

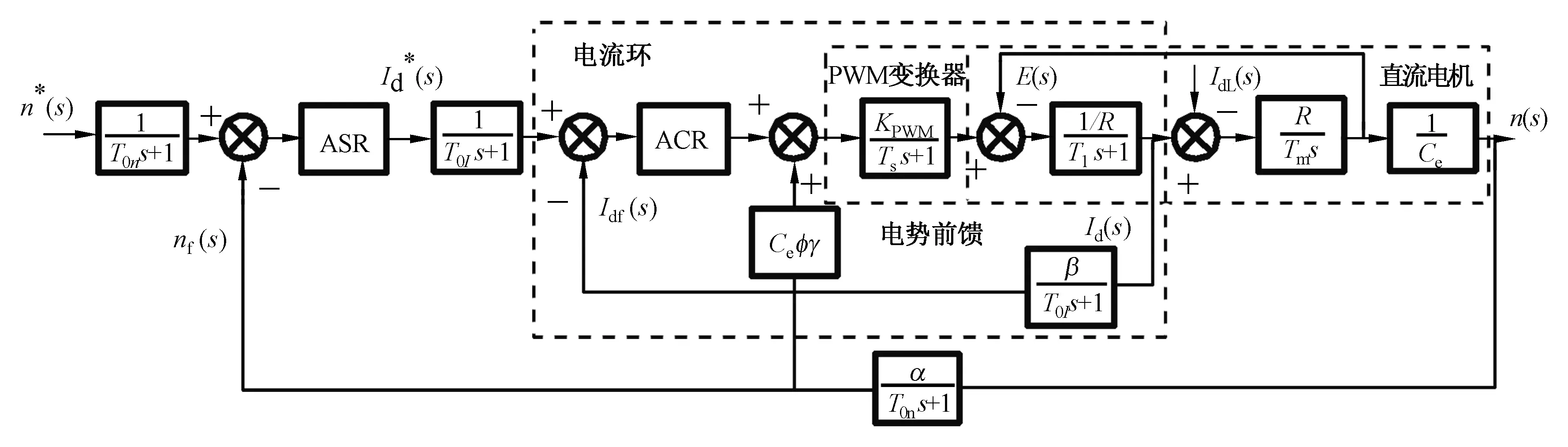
图4 双闭环直流调速系统动态结构图Fig.4 Block diagram of dynamic DC motor drive system with double closed loop

1.2 传统PID控制闭环分析

传统的双闭环控制直流电机调速系统中电流调节器ACR和转速调节器ASR一般采用PID结构形式，转速ASR和电枢电流ACR调节器的PID控制器均可表示为如图5所示结构。PID调节器由比例环节、积分环节和微分环节三部分组成，vin表示输入量(转速给定和电流给定)，vout表示被控对象的输出量(电枢电流，电机转速)。

图5 PID控制系统框图Fig.5 Block diagram of control system with PID controller

PID控制器的输出量u与输入误差e的连续域表达式为

(9)

对PID表达式离散化后得到其增量表达式为

(10)

式中，kp、ki和kd分别为比例调节系数、积分调节系数和微分调节系数，Ts为直流电机调速系统转速闭环控制的采样周期,即开关周期。

封网作业车的直流电机的电流环为传统PID调节器，要求PID设计参数满足电枢电流动态响应特性，最终使得系统运行时能够保证电枢电流超调量、调节时间、上升时间等动态指标满足要求，为此，要求电流环具有高跟随性能，其传递函数设计为典型I型系统。

假设电流调节器为PI调节器，调节器的比例系数为kpI，积分系数为kiI，则图4所示直流调速系统图中电枢电流环闭环传递函数为

(11)

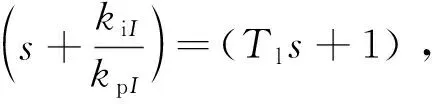
(12)

(13)

(14)

其中，

由传递函数式(14)可见，转速闭环系统为含有零点的二阶系统，则调速系统转速阶跃响应参数中超调量为

(15)

其中，

上升时间为

(16)

调节时间为

(17)

同理，电枢电流扰动与转速之间的闭环传递函数为

由直流电机的转速动态性能指标式(15)～(17)以及传递函数式(14)可见，当Tm因直流电机的转动惯量变化时，理想情况下，如果保持转速调节器比例积分系数kpn和kin随Tm变化，则可实现转速控制的动态性能指标不变。反之，根据直流电机转速阶跃响应特性在线修正转速调节器比例、积分、微分系数可优化PID转速调节器控制的动态性能。由式(15)～(17)可见，转速调节器比例积分微分系数与转速阶跃响应之间为非线性关系，因此本文提出适于解决此非线性问题的BP神经网络PID参数优化控制方案。

2 BP神经网络PID控制及参数优化

由于传统PID控制器中三个调节参数固定不变，当输电线路作业车面临作业环境的非线性和时变不确定性，该控制方法无法满足复杂场合下对电机高精度及高性能的要求。BP神经网络同时兼备学习和记忆两种功能，适合用于解决非线性、不确定系统的控制问题，本文将PID控制器和BP神经网络进行结合，对PID参数实时调整，从而实现复杂场合下提高直流电机转速动态性能和转速控制精度，进而提高直驱式封网作业车直流电机调速系统抗负载扰动能力。

封网作业车电机BP神经网络PID控制系统框图如图6所示，其中BP神经网络的输入量为封网作业车直流电机转速参考值n*，转速为n，转速误差为e,BP神经网络的输出信号为PID控制器参数系数kp、ki、kd，PID控制器输出信号u为直流电机电枢电流给定信号，直流电机电枢电流调节器ACR仍为图4所示的传统PID调节器，nN为直流电机的额定转速。

图6 BP神经网络PID控制系统Fig.6 Control system with BP-NN PID controller

图7 三层BP神经网络框图Fig.7 Block diagram of three-layer BP neural network

本文设置BP神经网络为包含输入层、隐含层、输出层的3层结构，其中输入层和输出层神经元个数为3，隐含层中包含的神经元个数为8，隐含层和输出层激活函数分别为正负对称的Sigmoid函数f(x)和非负的Sigmoid函数g(x)，本文中BP神经网络PID控制器的具体算法为：

(18)

(19)

隐含层的神经元输入和输出量分别为

(20)

(21)

输出层神经元的输入和输出量分别为

(22)

(23)

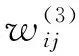
隐含层函数为双极性Sigmoid函数，

(24)

其导数为

(25)

输出层函数为单极性Sigmoid函数，

(26)

其导数为

g′(x)=αg(x)[1-g(x)]。

(27)

BP神经网络PID调节器系数kp、ki和kd分别为

(28)

下面讨论BP神经网络PID控制策略的误差反向传播算法。首先设定神经网络权重系数修正的指标函数为

(29)

按照梯度下降法加惯性项的算法，多次迭代修正图7中所示神经元的连接权重，第κ次迭代计算BP神经网络隐含层元i与输出层神经元l连接权重系数增量Δwil(κ)为

(30)

同时，第κ次迭代计算BP神经网络输入层神经元j与隐含层神经元i连接权重系数增量为

(31)

式中，η1，η2为学习率，α1、α2为惯性系数。

根据PID的表达式(10)，求出式(30)和(31)中的部分偏导数并标幺化处理后写为

(32)

将式(25)、(27)、(29)、(32)代入式(30)，最终隐含层神经元i与输出层神经元l的连接权重系数的增量函数Δwil(κ)可以表示为

(33)

输入层神经元j与隐含层神经元i连接权重系数的增量函数Δwji(κ)可以表示为

(34)

图8为直流电机BP神经网络PID控制的流程图。

图8 直流电机BP-NN PID控制流程图Fig.8 Flow chart of BP-NN PID control for DC motor

3 仿真验证

利用MATLAB软件建立的直流电机转速BP神经网络PID优化控制仿真模型如图9所示，仿真参数如表1所示。

表1 直流电机调速系统仿真参数Tab.1 Parameters of DC motor driving system

图9 BP神经网络转速控制仿真模型Fig.9 Simulation model of BP neural network for speedcontrol

在直流调速系统的转动转动惯量为0.4 kg·m2情况下对BP神经网络PID控制的直流电机调速系统进行仿真，仿真时间设定为300 s，在仿真过程中通过加入转速给定的脉冲扰动对BP神经网络连接权重系数进行训练，最终得到BP神经网络PID控制的直流电机调速系统仿真波形如图10所示，其中图10(a)～(c)分别是以标幺值表示的神经网络输出的比例、积分和微分系数仿真波形，PID参数的基准值为1 000。由仿真波形可见，比例系数随时间变化的增量较小，认为其趋于稳定，积分和微分系数的波形收敛到较稳定值。图10(d)为转速给定n*和实际转速n的仿真波形，n在为恒定值0.2叠加幅值0.03的脉冲信号，脉冲周期为0.4 s，由n的仿真波形可见，神经网络PID控制的直流电机转速跟踪转速给定信号，实现了直流电机转速无静差控制，转速无超调，可见其转速控制动态快速性较好。

图10 转动惯量0.4 kg·m2 BP神经网络PID控制仿真波形Fig.10 Simulation waveform of BP neural network PID control under moment of inertia 0.4 kg·m2

在直流调速系统的转动惯量为0.1 kg·m2情况下对BP神经网络PID控制的直流电机调速系统进行仿真，再次训练BP神经网络的连接权重系数，仿真时间设定为300 s，292.5～294 s时间段仿真的放大波形如图11所示，其中图11(a)为转速给定n*和转速n的仿真波形，图11(b)为转速误差仿真波形，由仿真波形可见，直流电机输出转速仍然能够快速跟踪转速给定信号且转速静态误差为零。

在直流调速系统的转动惯量为0.1 kg·m2情况下采用传统PID控制对系统进行仿真对比分析以说明传统PID控制存在适应转动惯量变化能力较弱的问题，仿真波形如图12所示，传统PID比例积分微分系数与图10中300 s时刻BP神经网络输出PID系数相同，根据图10(a)～(c)分别得到PID系数分别为1 000倍0.68，0.1，0.596，由图12(a)可见直流电机输出转速能够跟踪转速给定信号且转速稳定，转速无超调，但对比图11(a)和12(a)的仿真结果，发现采用在转动惯量为0.4 kg·m2情况下训练神经网络得到的PID系数作为传统的PID控制器参数可适应转动惯量为0.1 kg·m2直流电机调速系统的稳定控制需要，但转速控制动态响应参数中的超调量小，封网机器人直流电机转速控制的快速性降低。图12(b)为直流电机电枢电流的仿真波形及其放大波形。

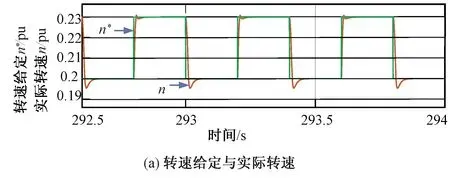
图11 转动惯量0.1 kg·m2 BP神经网络PID控制的仿真波形Fig.11 Simulation waveform of BP neural network PID control under the condition of inertia J=0.1 kg·m2

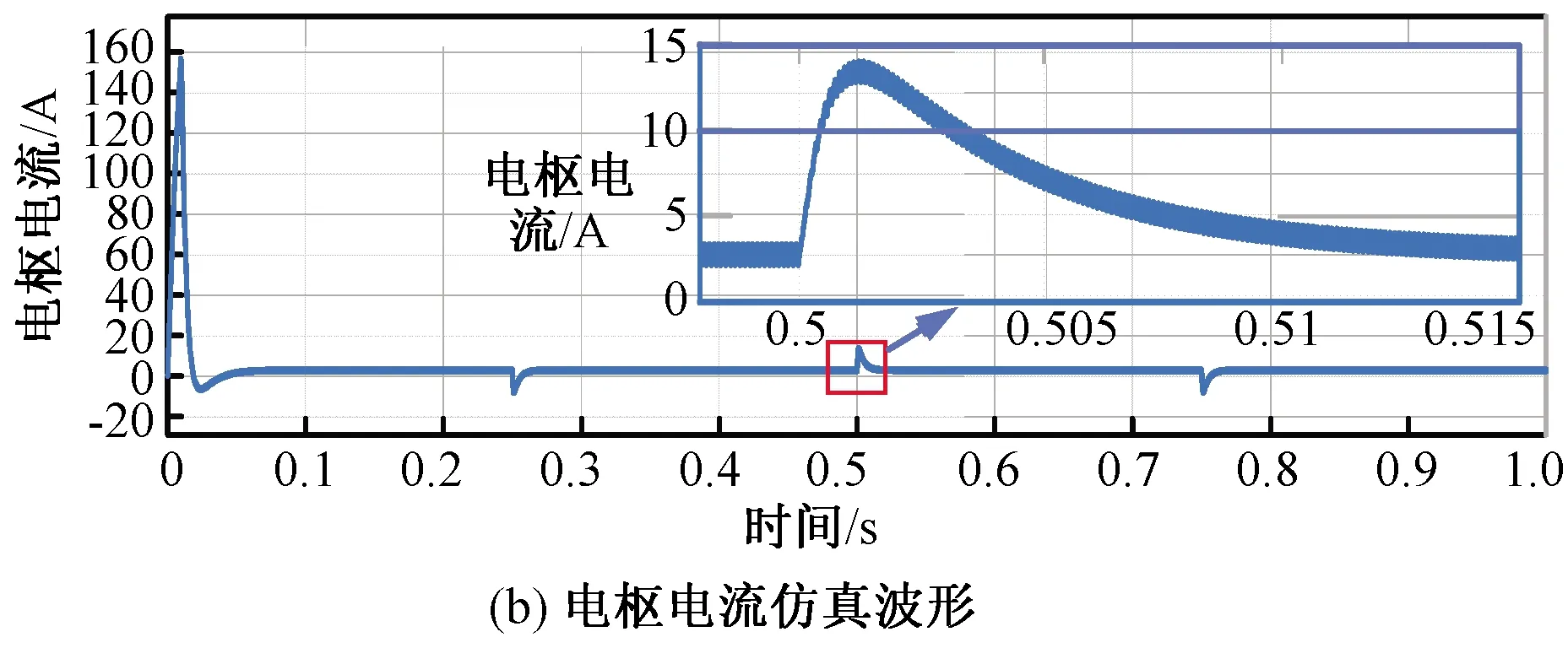
图12 转动惯量0.1 kg·m2传统PID控制仿真波形Fig.12 Simulation waveform of traditional PID control under the condition of inertia J=0.1 kg·m2

对比图10、图11和图12可见，相对于传统的PID控制，BP神经网络PID控制直流电机调速系统能够减小直流电机调速的超调量，提高转速响应时间，改善调速动态响应性能。

4 结论

为了使直驱式输电线路作业车直流调速系统适应负载变化等复杂工况，降低负载转动惯量变化对直流电机转速控制系统稳定性和控制性能的影响，最终实现降低作业车重量目的，提出了以转速闭环控制动态特性为优化目标的BP神经网络PID直流电机转速控制策略，改进了BP神经网络连接权重的修正方法，使得BP神经网络PID转速控制器进一步适应输电线路作业车在复杂作业环境下的调速要求，仿真对比表明，通过实时优化神经网络PID参数可提高输电线路作业车转速控制的动、静态性能。相对于传统的PID控制，BP神经网络PID控制直流电机调速系统能够减小调速的超调量、提高转速响应时间，改善调速动态响应性能。