基于事件时间间隔的VSI CQC-r控制图设计

张 莹，柯楚贤

（武汉理工大学 交通与物流工程学院，湖北 武汉 430063）

0 引言

控制图是统计过程控制（Statistics Process Control, SPC）的常用工具之一，最初用于监测生产过程的变化。随着对控制图研究的推进，学者们不再局限于监控缺陷的数量，而是将缺陷的发生定义为事件，以监控事件时间间隔（Time Between Events, TBE）为目的进行研究。由此TBE控制图的应用也拓展至物流效率、服务水平、灾祸预测等多个领域。

TBE 控制图主要包括服从指数分布的累积数量控制图（Cumulative Quantity Control, CQC）和服从几何分布的累积合格品数控制图（Cumulative Count of Conforming, CCC），本文研究的是CQC类控制图。

若将事件的发生视作泊松过程，其时间间隔服从指数分布，因此CQC 控制图也被称为指数图（exponential chart）。很多学者研究了指数图与经典控制图的结合和优化，如指数分布Shewhart型控制图、指数分布累积和（Cumulative Sum, CUSUM）控制图、指数分布指数加权移动平均（Exponentially Weighted Moving Average,EWMA）控制图、指数分布Run Rules 控制图等。Qu，等同时监控事件时间间隔与事件大小，设计了CUSUM统计量，并用于监控供应链的订货间隔和手足口病的发生。

Xie，等发现，CQC 图只根据当前检测情况进行判定而没有利用历史信息，在虚发警报概率较小时容易导致控制图误报和对过程偏移不敏感，因此以观察到r 个事件间的时间间隔为统计量，针对Erlang分布设计了t控制图，也即CQC-r图。由于Erlang分布是Gamma分布的特殊形式，Zhang，等将指数分布拓展为Gamma分布，设计了更为普遍的Gamma图，并使用平均报警时间（Average Time to Signal, ATS）作为性能指标，证明基于随机位移模型的CQC-4图与改进的指数CUSUM 图性能相当，但更易于理解和使用。由于Gamma 分布的偏斜导致控制图的有偏，Yang，等提出了尺度参数已知和未知情况下ATS 无偏的CQC-r图设计，并使用序贯抽样使控制图尽快开始监控。Kumar，等将文献[6][12]的指数图运行规则推广到CQC-r图，利用马尔科夫链计算平均运行长度（Average Run Length，ARL），并比较了不同运行规则对不同偏移范围的适用性。CQC-r图的应用上，Xie，等将CQC-r 图用于监控故障时间数据，Liu，等将CQC-r图用于开发管材生产过程的在线监控系统，并说明CQC-r图比指数CUSUM和指数EWMA控制图更加通用和灵活。

变采样间隔（Variable Sampling Intervals，VSI）是改进控制图常用的方法之一。传统的固定采样间隔（Fixed Sampling Intervals，FSI）控制图中，两次采样间的间隔为定值，而VSI控制图中采样间隔取决于前一次采样的结果，因此能够利用历史信息缩短控制图发现异常的时间。VSI 在传统控制图中的应用较为常见，如Nguyen，等的VSI Shewhart多元变异系数控制图、薛丽的不合格品率二项分布VSI CUSUM 控制图、Tran，等的VSI EWMA中值控制图、张艳，等的VSSI EWMA预防维修控制图。万强研究了双抽样调整抽样间隔型np 控制图DSVSI np 的经济性设计。对于TBE数据，Liu，等提出了VSI CCC控制图，并由Nezhad，等延伸至VSI CCC-r 图，证明了VSI CCC-r图总是比FSI CCC-r图更有效。Zhang，等研究了贝叶斯估计下的VSI CCC 图性能，根据目标的ATS 及其标准差SDTS（Standard Deviation of Time to Signal，SDTS）给 出 了 所 需 要 的Phase I 样 本 数。Zhang，等将VSI用于改进指数分布的CQC图，最优采样间隔组合下，改进后控制图的ATS平均约为固定采样间隔CQC图的85%。

可见CQC-r图在多个领域中都能发挥较好的过程监控效果，同时变采样间隔策略能缩短控制图的报警时间，提高检测速度。但目前对动态TBE控制图的研究主要停留在二项分布的CCC类图，还未有学者研究变采样间隔策略对CQC-r图的影响。因此本文基于TBE数据，将VSI策略应用至Gamma分布CQC-r图，对VSI CQC-r图的性能进行研究，并通过监控订货间隔的案例验证VSI CQC-r图在供应链管理中的有效性。

1 FSI CQC-r控制图

事件的发生是一个泊松过程。若用统计量T表示恰好检测到一个目标异常事件所经过的时间，则T服从指数分布，其累积分布函数为：

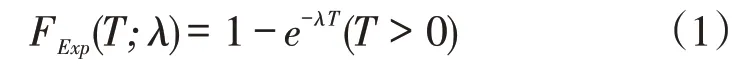
其中为逆尺度参数（inverse scale parameter），为正数，代表了事件的发生率。FSI CQC控制图监控统计量T，T 落在控制限之外说明事件的发生率超过预先设定的可接受范围，过程可能出现异常，需要进行检修。

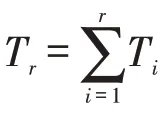
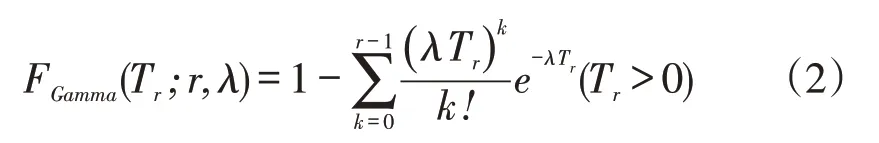
其中r为Gamma分布的形状参数（shape parameter），为正整数，表示FSI CQC-r 图关注的是连续r 个事件；为对应指数分布的逆尺度参数。当r=1 时，Gamma 分布即为指数分布，FSI CQC-1 图即为FSI CQC图。

当控制图使用者想观察的连续事件数r确定时，事件发生率越高，出现r个事件需要的时间越短，在控制图上反映为统计量的向下偏移，也即使用者往往对T减小的向下偏移更感兴趣。因此本文研究的是检测TBE减小的下单边控制图。给定受控状态下可接受的虚发警报概率，下单边FSI CQC-r图的下控制限（Lower Control Limit，LCL）满足：

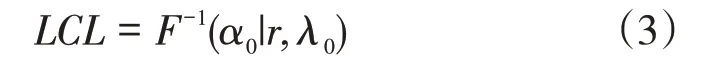
其中F()为Gamma分布的逆函数，为受控状态下目标事件的发生率，一般可由经验得出。

2 VSI CQC-r控制图

FSI策略下，控制图每次采样的时间间隔相同，但VSI策略下，第i+1次采样使用的间隔h取决于第i次采样的结果T。若过程波动较小、预测过程运行良好，下次采样使用较大的采样间隔h，过程发生较大波动则使用较小的采样间隔h。同时为了在控制图运行初期提供额外的保护，首个间隔h将使用较短的采样间隔h。

一般的下单边FSI控制图只有一条下控制限，当统计量落入下控制限以下时报警。VSI控制图中增加了下警戒限LWL（Lower Warning Limit，LWL），本文中还添加了均值线ML（Median Line，ML）。对于本文的下单边VSI CQC-r图，设置采样间隔h=（h，h，h）和控制限（LCL，LWL，ML），且0＜h＜h＜h，0＜LCL＜LWL＜ML，其中ML 取Gamma 分布的期望(T)，h表示与FSI控制图相同的采样间隔。

LCL、LWL、ML将控制图划分为四个区域。根据每次采样时统计量T所处的区域，过程可能处于不同的状态，VSI控制图将不断调整采样间隔。VSI策略中对采样间隔的选择可由式（4）表示，每个区域的采样策略如下：

（1）内部安全区(ML，+∞)：此时事件时间间隔大于对应Gamma分布的期望，过程运行良好。为降低采样和检测的成本，下次采样使用较长的间隔h；

（2）外部安全区(LWL，ML]：此时过程可能保持稳定。为进一步观察，下次采样使用适中的间隔h；

（3）警戒区(LCL，LWL]：此时时间间隔有缩短的迹象，事件发生率可能增大，需要尽快采样确定过程状态，下次采样使用较短的间隔h；

（4）失控区(0，LCL]：此时事件时间间隔缩短并超过可接受的范围，说明过程已经失控，需要立即采取相关措施，及时查明并排除导致异常的原因，保持过程稳定。

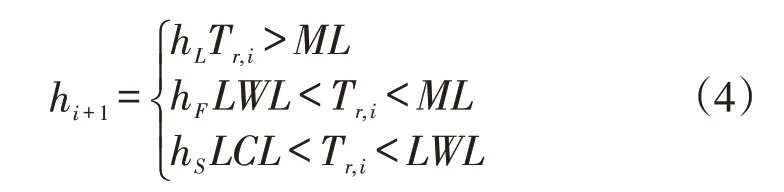
记统计量落在不同区域的概率为p，i=1，…，4，则VSI CQC-r 图的各控制限及统计量落在各区域的概率满足式（5）-式（9）。

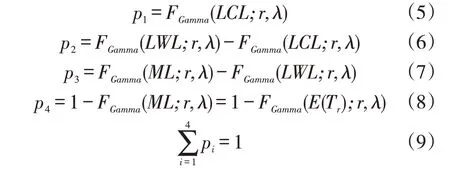
其中(T) 为Gamma 分布() 的期望。VSI CQC-r图各区域示意图如图1所示。

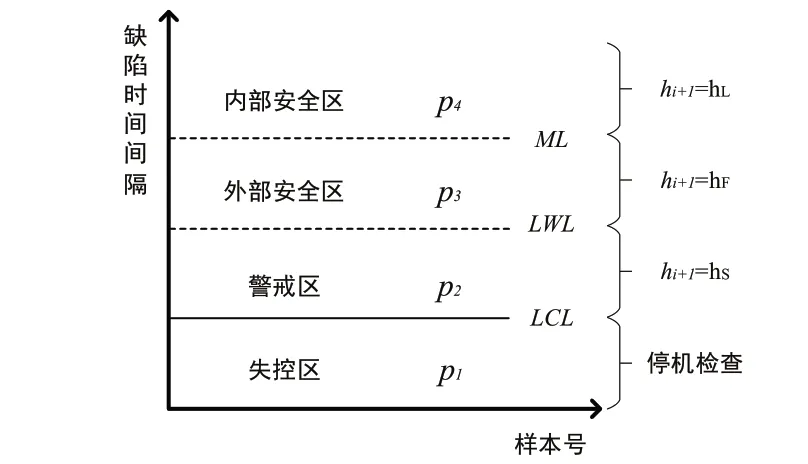
图1 VSI CQC-r图各区域示意图

3 评价标准

平均运行长度ARL是评价控制图的常用标准，代表了控制图从开始运行到发出警报时所经过的平均样本个数。假设失控状态下过程的事件发生率由偏移至，则统计量T落在LCL之上、即控制图未发出警报的概率为漏发警报概率，有：

ARL反应了控制图发出警报时运行过的平均样本个数，但VSI控制图还关注报警所需要的时间，因此VSI CQC-r图应该以平均报警时间作为性能指标。平均报警时间ATS 为ARL 与平均采样间隔ASI（Average Sampling Interval，ASI）的乘积，表示控制图从运行开始到报警所需要的平均时间。FSI控制图的平均采样间隔ASI为一常数，VSI 控制图的平均采样间隔ASI为采样间隔的随机变量，表示为采样间隔的期望值，即：

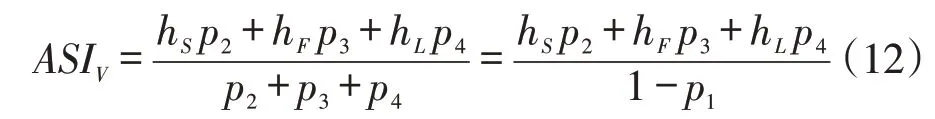
则VSI CQC-r图的平均报警时间可表示为：

当h=h=h时，控制图使用的是FSI策略，有：

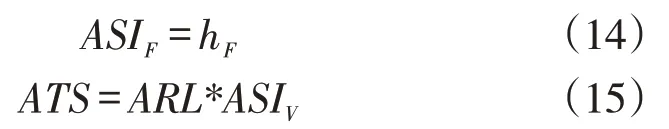
与ARL的比较类似，受控ATS相等的前提下，失控ATS越小，控制图越能更快地检测到异常的发生。

4 性能分析

4.1 VSI CQC-r控制图的求解

为方便表述，令ATS和ATS分别表示不同形状参数r 对应的FSI 和VSI 策略下CQC-r 图的受控ATS，同理将失控ATS表示为ATS和ATS，受控ASI表示为ASI和ASI。

控制图的设计、求解和比较要求在受控ATS相等的前提下尽量减小失控ATS。为了比较VSI和FSI策略对过程失控的检出效果，求解时需要控制ATS=ATS。同时VSI控制图为避免采样频率对结果的影响，还要求受控状态下VSI 和FSI 控制图的平均采样间隔相等，即ASI=ASI。此时VSI CQC-r图的求解可以转化为一个非线性方程组求解问题：

即在受控ATS和ASI相等的条件下，求解使失控ATS最小的控制限。

为了方便比较不同控制图的性能，本文与其他论文类似，取0002 7 。不失一般性，取ASI=ASI=h=1。同时为简化求解过程，本文参照文献[22]给其他参数设置了一定的取值范围：形状参数r ∈{1,2,3,4}，受控逆尺度参数0000 5 ，过程偏移∈{1.0，1.1，1.2，1.3，1.4，1.5，1.6，1.7，1.8，1.9，2.0，3.0｝，采样间隔h ∈｛（0.8，1.0，1.2），（0.7，1.0，1.3），（0.5，1.0，1.5），（0.3，1.0，1.7），（0.1，1.0，1.9）｝。

4.2 变采样间隔对CQC-r图的影响

改进因子表示了过程发生偏移时VSI与FSI策略对CQC-r 图性能的影响，改进因子越小，VSI 策略对CQC-r图的提升越大。特殊的，当r=1时，恰好检测到一个目标异常事件所经过的平均时间服从指数分布，即表示VSI CQC图对FSI CQC图的改进因子。

根据式(16)，求解不同形状参数、过程偏移、采样间隔下VSI CQC-r图对FSI CQC-r图的改进因子如图2所示。

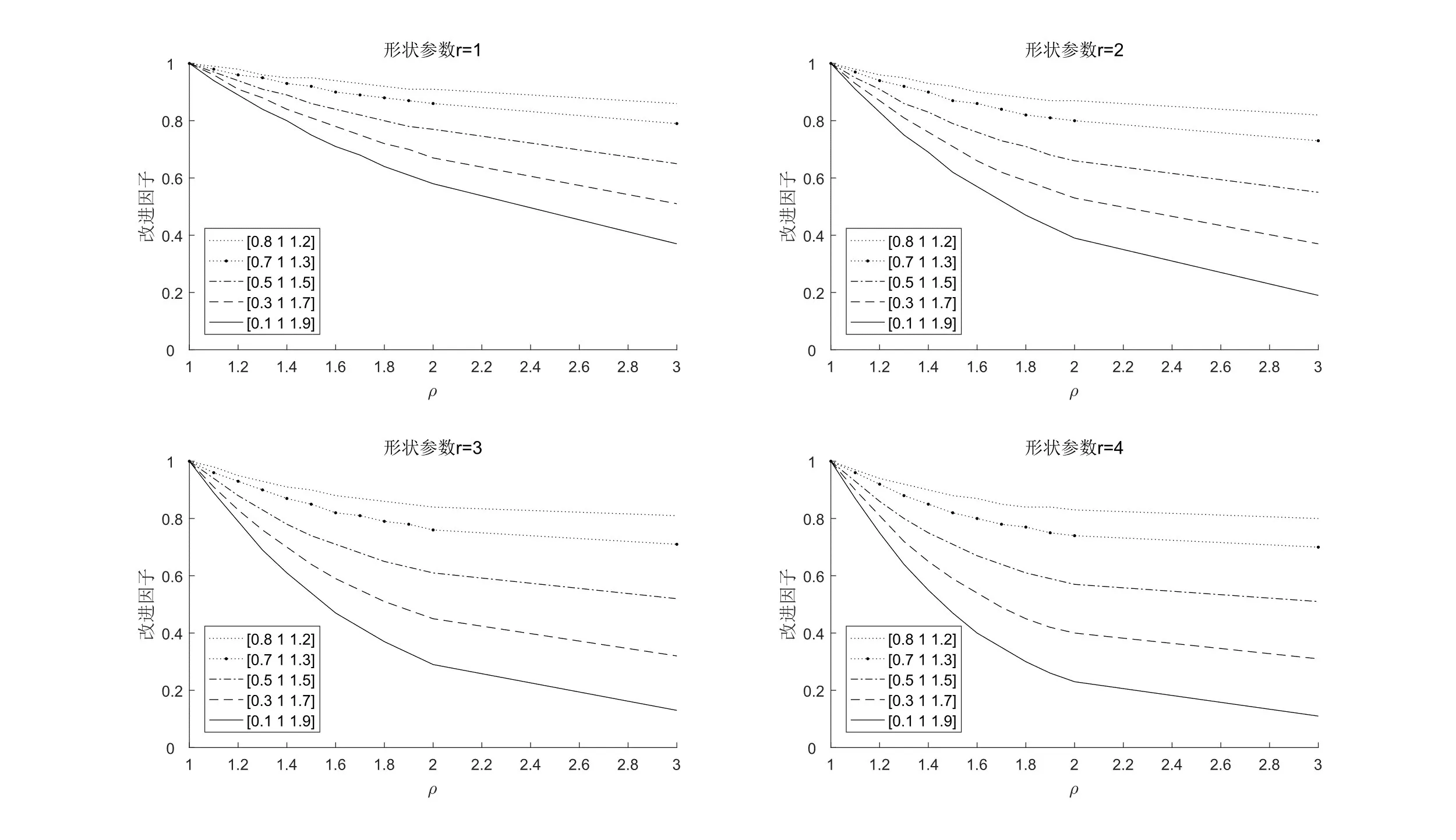
图2 VSI CQC-r图对FSI CQC-r图的改进因子(r=1,2,3,4)

由于改进因子越小，改进后的图表对原图表的提升越大，可见VSI策略对CQC-r图有一定的改进。形状参数r固定时，对于相同的过程偏移，采样间隔的差值(h-h)越大，VSI对CQC-r图的改进效果越好，采样间隔的差值最大时图表效果达到最优。对于相同的形状参数和采样间隔，过程偏移越大，VSI对CQC-r图的改进越大，如=19 时，h=(0.1,1.0,1.9)的VSI CQC-4图的平均报警时间仅为FSI CQC-4图的25%，控制图检测出失控的速度明显提高。

在实际应用中，采样间隔的设置受过程流畅性要求、控制图使用者偏好、可接受的最长最短采样间隔等多种因素的影响，不能简单地使间隔的差值越大越好。通过使用不同的r值可以帮助设置采样间隔。如=19 时，h=（0.1，1.0，1.9）的VSI CQC-2图有ATS=97 047，而h=（0.3，1.0，1.7）时有ATS=97 028、h=（0.5，1.0，1.5）时有ATS=104 510，即增大r值能超过或接近r较小时VSI CQC-r图的最优效果，且可选的采样间隔组合增多。因此在期望的检测速度下可以更灵活地选择不同参数组合，在保证检测效果的前提下方便实际操作。结果见表1。

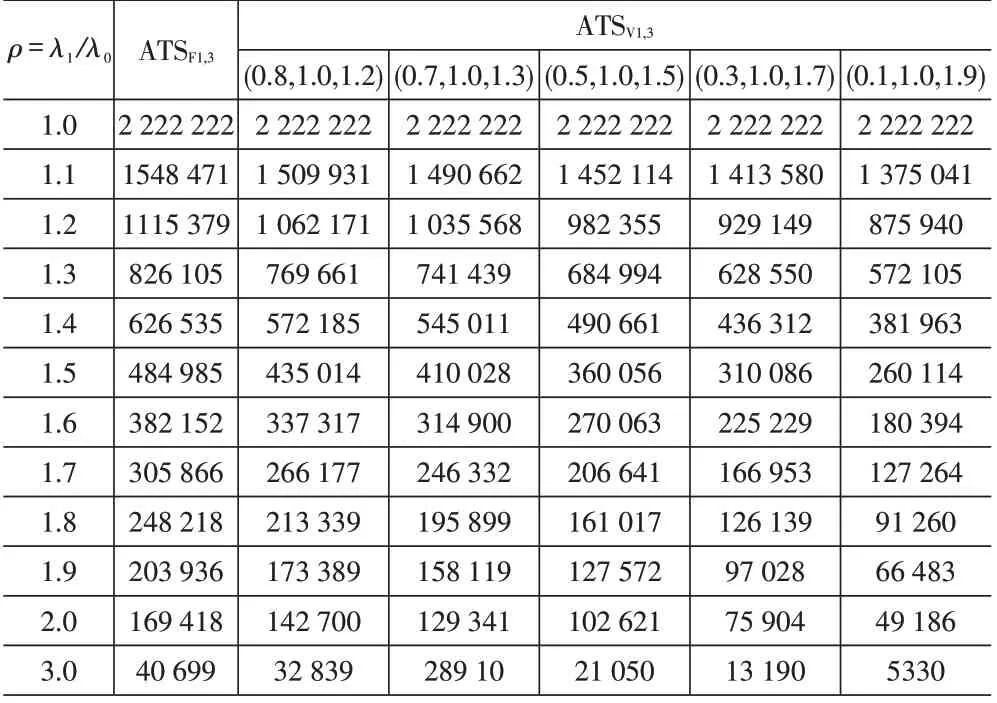
表1 不同采样间隔组合和偏移下VSI CQC-r图和FSI CQC-r图的ATS(r=3)

4.3 形状参数对VSI CQC-r图的影响

为更直观地分析形状参数取值对VSI CQC-r 图性能的影响，不同r值对应的ATS值如图3所示，见表2。由上节可知，形状参数与过程偏移相同时，采样间隔的差值越大，VSI CQC-r图的性能越好，因此仅分析性能最优的采样间隔为(0.1，1.0，1.9)时的情况。为方便观察，纵坐标取自然对数ln(ATS)。

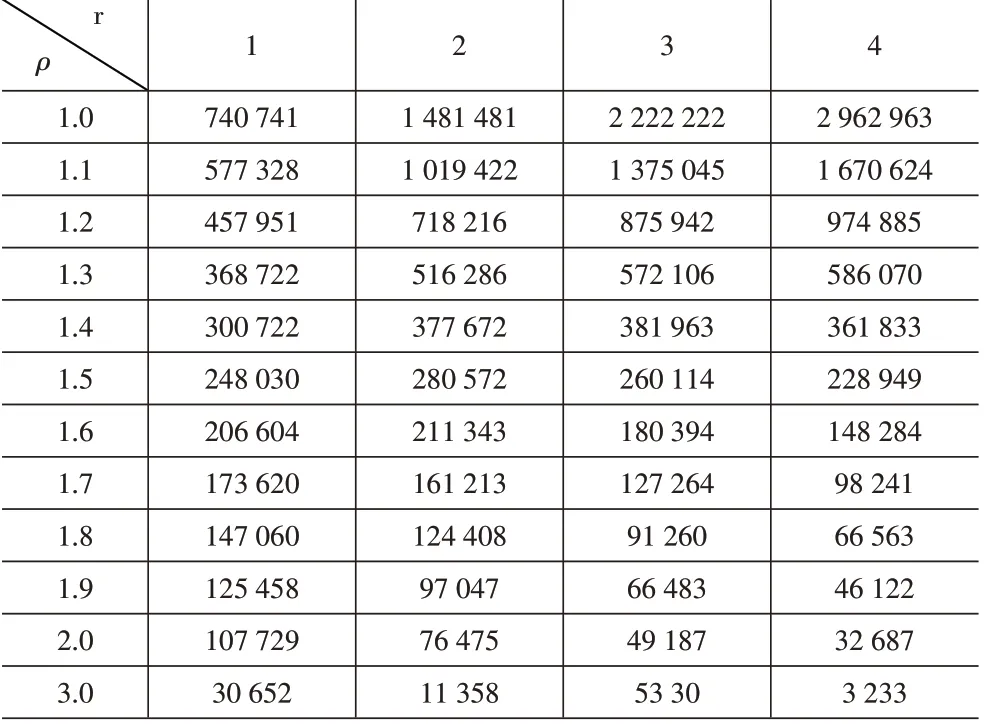
表2 不同形状参数和偏移下VSI CQC-r图的ATSV1,r(h=(0.1，1.0，1.9))

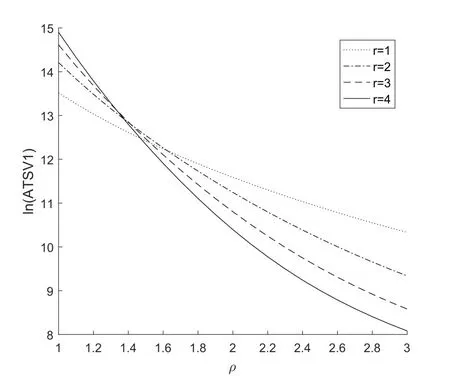
图3 形状参数对VSI CQC-r图的影响（h=（0.1，1.0，1.9))

由图可知，无论形状参数如何取值，随着过程偏移增大ATS都逐渐减小，控制图的性能提升。随着偏移增大，VSI CQC-r图检测大偏移的性能提升，且r越大检出速度越快。虚发警报概率和过程偏移一定时，由式（3）和式（10）可知，r越大，VSI CQC-r图的LCL越大、漏发警报概率越小，符合控制图固定可接受的虚发警报概率、并使漏发警报概率尽量小的优化方向。

但形状参数越大，VSI CQC-r图对小偏移越不敏感。由ATS的定义可知，较小时，ATS受r的影响变化较剧烈。虽然增大形状参数能提升对大偏移的检测效果，但在偏移足够大时，各VSI CQC-r图的差距已经不大。由于过大的r值可能会掩盖过程已经发生偏移的问题、延长发现事件的时间，实际应用中可以事先根据经验和应用环境，预估可能产生的偏移范围，综合考虑检测效果和计算速度选择合适的形状参数。

5 实例分析

孟玥，等指出，统计过程控制在供应链风险管理中能发挥相当的作用。本节使用VSI CQC-r 图监控TBE数据，说明VSI CQC-r图的运行过程和在供应链管理中的应用。

根据文献[7]，存在一个由批发商、贸易公司、零售商组成的农产品供应链，其中贸易公司使用统计过程控制监控下游零售商的大米订货间隔。当下游订货间隔缩短、对大米的需求超出预期时，贸易公司向上游批发商发出追加订单，以保证供应的稳定性。根据过往记录，受控状态下下游两次订货的间隔服从0495 的指数分布，即平均每2.02小时有一大米订货需求。自第31次订货起，零售商的需求增加，订货间隔服从198 的指数分布，即平均每0.51小时有一大米订货需求。

由于采样间隔的差值越大、VSI CQC-r图的检测效果越好，取h=(0.1,1.0,1.9)。设置误报率T=0.002 7，形状参数r=3，使用VSI CQC-3图对订货间隔进行监控，由式（16）可计算VSI CQC-3 图的控制限LCL=0.55，LWL=4.81，ML=6.06。每三个订货间隔的数据见表3，其中前10 个为受控状态，后10 个为失控状态。使用VSI CQC-3图监控的结果如图4所示。

表3 大米供应链中零售商的订货间隔Tr

图4 VSI CQC-3图监控大米订货间隔（h=（0.1，1.0，1.9））

VSI CQC-3 图的运行中，根据变采样间隔策略，首次采样使用了较小的间隔h，且此时统计量位于警戒区，下次采样也使用h；在第4次采样使用了h、第3次采样使用了h。从第10个样本点之后，订货过程发生了偏移，FSI CQC-3图和VSI CQC-3图都在第14个样本点检测出过程异常。但从过程发生偏移到控制图报警，FSI CQC-r图运行了4个小时，VSI CQC-3图仅运行了3.1小时，检测出异常的时间缩短了22.5%。检出下游需求增加时间缩短使贸易公司能更快做出响应，通过增加上游订货量、调整物流策略等方式维持供应链的正常运行。

6 结语

本文主要描述了Gamma 分布下变采样间隔的VSI CQC-r图的设计，并利用平均报警时间ATS分析了VSI CQC-r图的性能。研究发现，过程偏移相同时采样间隔的差值(h-h)越大，或形状参数和采样间隔相同时过程偏移越大，变采样间隔策略对CQC-r图的改进越大。同时发现调节参数组合可以使不同参数的图表达到相近的效果，提高使用灵活性。通过进一步分析发现，r 的增大使VSI CQC-r 图能更快检测出大偏移，但对小偏移的检测速度下降。

由于VSI CQC-r图的性能受形状参数、过程偏移和采样间隔的共同影响，实际应用中对偏移范围的估计对图表参数的选择有指导作用。如何估计过程参数，将VSI CQC-r图应用于参数未知或分布未知的过程也可进一步研究。同时本文的控制图设计仅考虑了统计性能，可以考虑设备故障的经济性设计能提高控制图的综合效益。