行李输送系统流量稳定控制策略
李 俊,李 霖,吕霄霄,任科冀,陈永洪
(1.成都天府国际机场建设指挥部,四川 成都 641400;2.重庆大学 机械传动国家重点实验室,重庆 400044)
0 引言
随着机场客流量的持续增长,为保障航班正点,要求机场提供更为安全和高效的进出港服务。行李系统是保障航班正点,提升机场服务的关键系统之一,主要提供:值机托运、早到存储、自动分拣、中转联程等服务。行李系统的处理能力是机场客流量最基本的保证,也是衡量机场自动化高低的标准,而行李系统的处理能力受限于行李系统的流量控制技术。然而,许多机场在设计行李系统时并没有考虑流量控制技术在系统中的应用。比如西南某机场在设计行李系统时未考虑到行李系统与安检机的流量控制问题,导致行李在安检过程中的流量不平衡,降低了系统运行的稳定性。华东某机场在设计行李小车系统时,未考虑系统分流、合流点流量平衡问题,导致行李系统故障频发,影响航班正点起飞。
本文在分析行李输送过程中流量不平衡因素对行李系统处理能力影响的基础上,提出间距控制和间隙控制两种流量控制策略并建立相应数学模型,设计缓存输送机并模拟分析系统的缓存能力和流量稳定性,为提升机场客流量提供理论基础。
1 输送机处理能力的定义
输送机处理能力是指在一定的时间范围内(通常为1小时),物件通过某一测量位置的数量。如图1所示。上游输送机上的物件为j+1,下游输送机上的物件为j。定义上游输送机的编号为i,下游输送机编号为i+1,设备i的速度为V,单位为m/s(其中,i=1,2,3…N,N为输送线输送机设备的总数)。设单个设备一个小时处理能力为C件(物件连续通过输送机),控制物件的窗口长度为W,单位为m。

图1 输送机上下游示意图
输送机的处理能力为:

本文讨论的处理能力是单条输送机线的设计处理能力,它是在理想情况下单条输送线所能达到的处理能力。主要基于下述条件:(1)物件的长度是平均长度;(2)处理能力是基于窗口控制模式;(3)系统没有故障和例外情况发生;(4)系统的输入是连续并且周期性的。
2 渐停对物件运动及系统性能的影响
当物件j+1到达输送机末端时,若物件j+1与j之间的距离L小于设定值,系统会停止输送机i,直到L满足条件再恢复输送机V=1的运转。条件不满足时,系统将输送机V=1停止的行为称为渐停,通常情况下系统渐停是由于系统流量不平衡导致的。每发生一次渐停,就会增加物件在输送机上输送的时间。渐停与输送机的传输距离也有直接的关系,输送机匀速运行一小时,输送带传输距离是3 600m,假设输送机的速度V=1。当渐停发生时,输送机表面的速度如图2所示。

图2 一次渐停的速度变化
由图2可知,渐停时间内输送机运行的距离小于V×(T+T)(T为输送机的减速时间,T为输送机的加速时间)。渐停过程的加速度难以得到,并且输送机的控制精度要求相对较低,因此将加速度设定为固定值,如图3所示。

图3 简化后的加减速过程
因此,可以得到输送机减速过程的加速度a=-V/T,同理可以得到输送机加速过程的加速度a=V/T,于是:

若一小时内发生k次渐停,则该小时内输送机的输送距离为:

依据经验,设V=1m/s,T=0.25s,T=0.5s,带入式(3)可得:

由式(4)得到渐停次数与输送机传输距离之间的关系,如图4所示。

图4 输送机运行距离与渐停次数关系图
由图4可知,随着渐停次数的增加,输送机传输的距离减少,即处理能力降低,降低的比率为:

由式(1)、(4)、(5)可得,随着渐停的次数逐渐增加,系统处理能力降低,如图5所示。

图5 处理能力下降的百分比与渐停次数之间关系图
3 流量控制的基本方法
流量控制的时候需考虑以下两个前提条件:
(1)检测物件位置的传感器需要配置滤波,以防止物件的附属物品对控制逻辑产生影响,避免输送机频繁启动与停止;
(2)下游输送机的处理能力要比上游的输送能力高,并根据实际情况逐级放大。
流量控制的最基本方法有两种,一种是控制两个物件前端与前端之间的距离,称之为间距控制,控制间距定义为L;另一种是控制前一件物件的尾端与后一件物件前端之间的间隙,称之为间隙控制,控制间隙定义为L。设物件的长度是L,如图6 所示。为保证系统稳定性,控制的最基本的条件是C≥C。

图6 流量控制的基本参数示意图
采用不同的控制方法,单位小时内通过单个设备的物件的数量计算方法不同。采用间距控制的时候,通常L>L,单位小时内处理量关系式为:

其中,M为采用间距控制时一小时内通过输送机的行李数量。
如果采用间隙控制,单位小时通过的物件数量受到物件长度的影响,如下:

其中,M为一小时内采用间隙控制通过输送机的行李数量。
因此在瞬时情况下,采用间隙控制时,单个设备的处理能力会根据物件长度的变化而变化,L越小,系统处理能力就越大。
式(6)和式(7)左侧值相同,则可知:

根据以上公式可得到不同控制方式的优缺点:
(1)间距控制会得到一个稳定的控制流量,但是物体之间的间距是一定的,若物件与之间的距离小于设定值,系统会停止输送机,直到满足条件再恢复输送机的运转,这种控制方式不利于提升系统的处理能力;
(2)在物件长度比较小的情况下,间隙控制会使系统的处理能力得到有效的提升,但间隙控制的处理能力会根据物件的长度变化而变化,系统无法得到一个相对稳定的处理量。
4 缓存输送机的设计
通过以上分析可知,无论采用间距控制还是间隙控制,为提高系统的性能,都需要采取进一步的措施,优化流量控制技术,这就需要输送机具备缓存的能力。所谓缓存能力,就是当某一截发生输送机停止运行时,上游的缓存输送机不会立马进入渐停状态,而应进入缓冲控制状态,以缓冲更多的行李,减少输送机渐停的次数,提高系统处理能力。具有缓冲能力的输送机就称之为缓冲输送机,它与普通输送机相比可以缓存更多行李,如图7所示。

图7 缓存输送机示意图
没有缓冲输送机的情况下,当j在输送机i+1上停止时,j+1立即进入渐停模式,j+2随即进入渐停模式,如图8所示。

图8 输送机传递物件示意图
假设L为缓存输送机,当物件j+1在L上发生渐停时,物件j+2不会立即进入渐停,而是还可传输△L=L-L距离之后,物件j+2才会在输送机i-1上进入渐停模式,如图9所示。输送机L的长度小于物件j+1与j+2之间的间距。

图9 三节输送机及传递物件示意图
如果在物件j+2传送到输送机i-1末端前,物件j+1 的状态从渐停转换为运转,物件j+2 就不会发生渐停,系统性能就不会降低,这就要求:

L为行李窗口W,根据式(1)可知:

由式(9)-(11)可得:

假设输送系统的处理能力保持不变,即C=C+1=C,式(12)可简化为:

由式(13)可知,若V≤V时L≤0,不能提升系统处理能力。只有V≥V时,才能提升系统处理能力,因此:
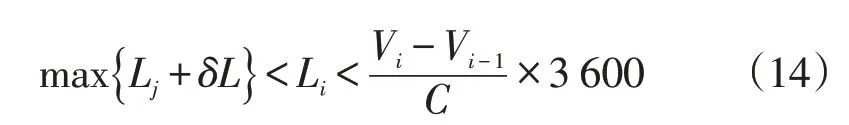
max{L+δL}为可输送物件长度,δL为物件的长度扰动,δL的值会因物件属性不同而有所不同。根据式(14)可计算出缓存输送机L的长度。
如果和配置之后仍然无法满足系统需求,则可以增加缓存输送机的数量来提升系统处理能力,这样式(14)可以转换成式(15):
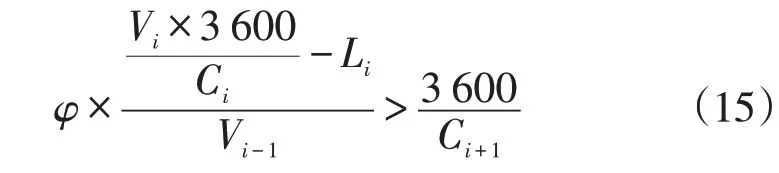
式(15)中φ为缓存输送机的数量,推导得到:

由式(16)可计算出缓冲输送机的数量。
5 数字仿真分析
结论验证在自主开发的仿真平台上进行,模拟行李在汇流过程中,增加一台缓冲输送机对系统流量平衡的作用。
如图10所示,左边系统在②输送线汇流处增加一台缓冲输送机。假设输送线①和②的处理量为900件/小时,设输送机速度为0.75m/s,缓冲输送机的速度为1m/s,根据式(15)可以计算出缓冲输送机的长度为1m。从输送线①和②分别注入不同行李量,观察汇流后输送线③行李量的变化。每组行李量测试持续10min,测试结果见表1。

图10 输送系统仿真

表1 有无缓冲机性能对比
由图11可以看出,增加缓冲输送机可平衡行李流量,可提高系统的稳定性。

图11 有无缓冲输送机对比折线图
6 结论
针对行李输送系统的流量稳定性而导致的行李输送系统故障率增加、处理能力降低等问题,研究工作的主要结论包括:
(1)提出一种基于间距控制的行李输送系统流量稳定控制方法,建立了系统处理能力、运输物体特性及皮带运行速度等数学模型;
(2)设计缓冲输送机并进行系统输送能力模拟仿真,其汇流后处理量降低比率可稳定在97%以上,具备良好的缓冲能力,能有效提升系统稳定性和处理量;
(3)在连续控制过程中,还有许多因输送机节点位置需要控制行李流量的情况及考虑系统缓存能力,可根据文中式(15)中的参数进行系统优化;
本文主要针对皮带式输送系统,除速度因素外还需要考虑输送机类型、表面材质、表面摩擦系数等对系统设计的条件限制,此类问题将作为后续的进一步研究内容。

